Tree Traversal

6,333 Comments / Trending / December 30, 2022

Traversal is the process of visiting all the nodes of a tree and printing their values. We always start from the root (head) node since all nodes are connected via edges (links). That is, we cannot reach a node in a tree at random. There are three methods for traversing a tree:

  • In-order Traversal
  • Pre-order Traversal
  • Post-order Traversal

In-order Traversal

This traversal technique visits the left subtree first, then the root, and finally the right subtree. It is important to note that every node might represent a subtree.

If a binary tree is traversed in ascending order, the result will be sorted key values.

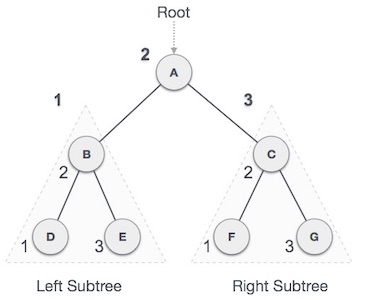
In Order Traversal
We start from A, and following in-order traversal, we move to its left subtree B. B is also traversed in-order. The process goes on until all the nodes are visited. The output of inorder traversal of this tree will be −
D → B → E → A → F → C → G

Pre-order Traversal

In this traversal method, the root node is visited first, then the left subtree and finally the right subtree.

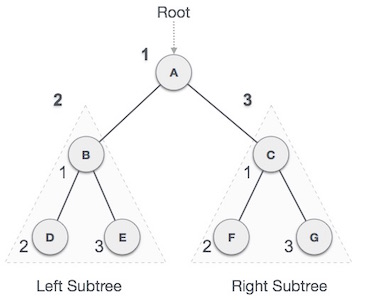
Pre Order Traversal

We start from A, and following pre-order traversal, we first visit A itself and then move to its left subtree B. B is also traversed pre-order. The process goes on until all the nodes are visited. The output of the pre-order traversal of this tree will be −

A → B → D → E → C → F → G

Post-order Traversal

The root node is inspected last in this traversal mode, thus the name. We go through the left subtree first, then the right subtree, and lastly the root node.

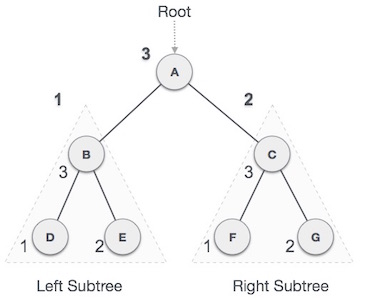
Post Order Traversal

We start from A, and following Post-order traversal, we first visit the left subtree B. B is also traversed post-order. The process goes on until all the nodes are visited. The output of the post-order traversal of this tree will be −

D → E → B → F → G → C → A

Share on Facebook
Tweet
0

No related posts.

6,333 thoughts on “Tree Traversal”

  3. cbd vapes canada

    Once I initially commented I clicked the -Notify me when new feedback are added- checkbox and now every time a remark is added I get 4 emails with the identical comment. Is there any method you may take away me from that service? Thanks!

    0
    Reply
  4. Taylor Garber

    Good day! I know this is kinda off topic but I’d figured I’d ask. Would you be interested in trading links or maybe guest writing a blog article or vice-versa? My website goes over a lot of the same topics as yours and I feel we could greatly benefit from each other. If you might be interested feel free to shoot me an e-mail. I look forward to hearing from you! Terrific blog by the way!

    0
    Reply
  6. kkslot777

    I have read several good stuff here. Definitely worth bookmarking for revisiting. I wonder how a lot effort you set to make one of these fantastic informative website.

    0
    Reply
  37. Slotbom88

    Hi there! This post couldn’t be written any better! Reading through this post reminds me of my previous room mate! He always kept talking about this. I will forward this article to him. Pretty sure he will have a good read. Thank you for sharing!

    0
    Reply
  120. Fungame777

    We stumbled over here by a different website and thought I might check things out. I like what I see so now i am following you. Look forward to looking at your web page again.

    0
    Reply
  122. Slotbom77

    An interesting discussion is worth comment. I think that you should write more on this topic, it might not be a taboo subject but generally people are not enough to speak on such topics. To the next. Cheers

    0
    Reply
  126. KKSLOT777

    Hello there! Do you know if they make any plugins to help with Search Engine Optimization? I’m trying to get my blog to rank for some targeted keywords but I’m not seeing very good results. If you know of any please share. Appreciate it!

    0
    Reply
  210. Kedai138

    I just like the helpful info you supply in your articles. I’ll bookmark your weblog and take a look at again right here frequently. I’m somewhat sure I will be told a lot of new stuff right here! Best of luck for the following!

    0
    Reply