Hash Table

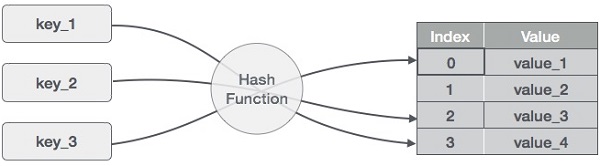
A hash table is a data structure that stores data associatively. Data is kept in an array format in a hash table, with each data value having its own unique index value. When we know the index of the needed data, we may get it extremely quickly.

As a result, it becomes a data structure in which insertion and search operations are extremely quick, regardless of the quantity of the data. Hash Tables use an array as a storage medium and employ the hash technique to establish an index from which an element is to be inserted or located.

Hashing

Hashing is a technique for converting a set of key values into a set of array indexes. To get a range of key values, we’ll utilize the modulo operator. Consider a hash table of size 20 with the following elements to be kept. Item is formatted as (key, value).

• (1,20)
• (2,70)
• (42,80)
• (4,25)
• (12,44)
• (14,32)
• (17,11)
• (13,78)
• (37,98)

Sr.No.	Key	Hash	Array Index
1	1	1 % 20 = 1	1
2	2	2 % 20 = 2	2
3	42	42 % 20 = 2	2
4	4	4 % 20 = 4	4
5	12	12 % 20 = 12	12
6	14	14 % 20 = 14	14
7	17	17 % 20 = 17	17
8	13	13 % 20 = 13	13
9	37	37 % 20 = 17	17

Linear Probing

As we can see, the hashing approach can be utilised to generate an array index that has already been used. In this situation, we can look into the following cell until we reach an empty cell to discover the next empty spot in the array. This method is known as linear probing.

Sr.No.	Key	Hash	Array Index	After Linear Probing, Array Index
1	1	1 % 20 = 1	1	1
2	2	2 % 20 = 2	2	2
3	42	42 % 20 = 2	2	3
4	4	4 % 20 = 4	4	4
5	12	12 % 20 = 12	12	12
6	14	14 % 20 = 14	14	14
7	17	17 % 20 = 17	17	17
8	13	13 % 20 = 13	13	13
9	37	37 % 20 = 17	17	18

Basic Operations

Following are the basic primary operations of a hash table.

• Search − Searches an element in a hash table.
• Insert − inserts an element in a hash table.
• delete − Deletes an element from a hash table.

Data Item

Define a data item having some data and key, based on which the search is to be conducted in a hash table.

struct DataItem {
   int data;
   int key;
};

Hash Method

Define a hashing method to compute the hash code of the key of the data item.

int hashCode(int key){
   return key % SIZE;
}

Search Operation

When searching for an element, compute the hash code of the key supplied and locate the element in the array using that hash code as an index. If the element is not located at the computed hash code, use linear probing to advance it.

Insert Operation

When inserting an element, compute the hash code of the key supplied and identify the index in the array using that hash code as an index. If an element is located at the computed hash code, use linear probing to find an empty position.

Delete Operation

Whenever an element needs to be deleted, compute the hash code of the key supplied and find the index in the array using that hash code as an index. If an element is not located at the computed hash code, use linear probing to advance it. When discovered, place a dummy item there to maintain the hash table’s efficiency.