When a dead end occurs in any iteration, the Depth First Search (DFS) method traverses a network in a depthward motion and uses a stack to remember to acquire the next vertex to start a search.
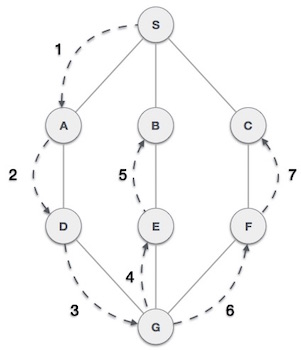
As in the example given above, DFS algorithm traverses from S to A to D to G to E to B first, then to F and lastly to C. It employs the following rules.
- Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Push it in a stack.
- Rule 2 − If no adjacent vertex is found, pop up a vertex from the stack. (It will pop up all the vertices from the stack, which do not have adjacent vertices.)
- Rule 3 − Repeat Rule 1 and Rule 2 until the stack is empty.
| Step | Traversal | Description |
|---|---|---|
| 1 | 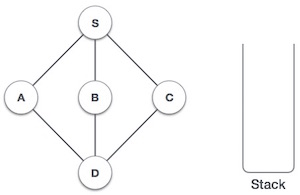 | Initialize the stack. |
| 2 | 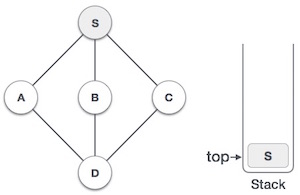 | Mark S as visited and put it onto the stack. Explore any unvisited adjacent node from S. We have three nodes and we can pick any of them. For this example, we shall take the node in an alphabetical order. |
| 3 | 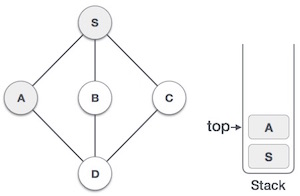 | Mark A as visited and put it onto the stack. Explore any unvisited adjacent node from A. Both S and D are adjacent to A but we are concerned for unvisited nodes only. |
| 4 | 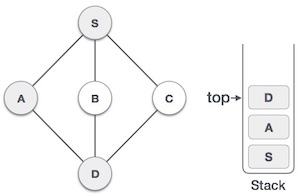 | Visit D and mark it as visited and put onto the stack. Here, we have B and C nodes, which are adjacent to D and both are unvisited. However, we shall again choose in an alphabetical order. |
| 5 | 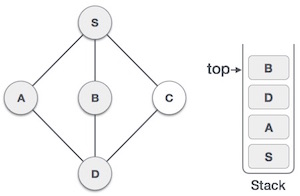 | We choose B, mark it as visited and put onto the stack. Here B does not have any unvisited adjacent node. So, we pop B from the stack. |
| 6 | 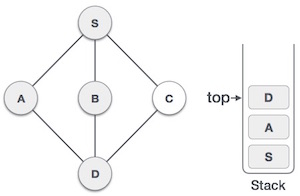 | We check the stack top for return to the previous node and check if it has any unvisited nodes. Here, we find D to be on the top of the stack. |
| 7 | 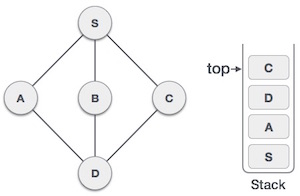 | Only unvisited adjacent node is from D is C now. So we visit C, mark it as visited and put it onto the stack. |
0
Your writing is perfect and complete. casino online However, I think it will be more wonderful if your post includes additional topics that I am thinking of. I have a lot of posts on my site similar to your topic. Would you like to visit once?
It¦s really a cool and useful piece of info. I am satisfied that you shared this helpful information with us. Please stay us up to date like this. Thanks for sharing.
There is visibly a bundle to identify about this. I feel you made some nice points in features also.
Hey very cool blog!! Man .. Beautiful .. Amazing .. I’ll bookmark your website and take the feeds also…I’m happy to find numerous useful info here in the post, we need work out more techniques in this regard, thanks for sharing. . . . . .
It’s a shame you don’t have a donate button! I’d without a doubt donate to this superb blog! I suppose for now i’ll settle for bookmarking and adding your RSS feed to my Google account. I look forward to fresh updates and will talk about this site with my Facebook group. Talk soon!
I am glad to be a visitor of this staring blog! , thankyou for this rare information! .
I rattling thankful to find this web site on bing, just what I was searching for : D also saved to fav.
3rd generation antihistamines list allergy medications prescription list claritin allergy sinus 12hr costco
strong dangerous sleeping pills 7 day sleep prescription
I’m still learning from you, but I’m improving myself. I certainly enjoy reading everything that is written on your site.Keep the stories coming. I enjoyed it!
buy deltasone 5mg pills buy prednisone 20mg generic
I respect your work, appreciate it for all the useful content.
best tablet for stomach pain roxithromycin 150 mg us
buy pills to treat acne order accutane acne medication by prescription
Thanks for another fantastic post. The place else could anyone get that type of info in such a perfect means of writing? I’ve a presentation next week, and I am at the search for such info.
An interesting discussion is worth comment. I think that you should write more on this topic, it might not be a taboo subject but generally people are not enough to speak on such topics. To the next. Cheers
Thanks for sharing superb informations. Your web site is very cool. I am impressed by the details that you have on this website. It reveals how nicely you perceive this subject. Bookmarked this web page, will come back for more articles. You, my friend, ROCK! I found just the info I already searched everywhere and just couldn’t come across. What a great website.
Regards for this wondrous post, I am glad I detected this site on yahoo.
best medications for heartburn biaxsig for sale online
absorica for sale online order accutane 40mg pills absorica for sale online
I value the blog post. Much obliged.
buying sleeping tablets on internet buy melatonin no prescription
order amoxicillin 250mg generic amoxicillin 500mg cost order amoxicillin 500mg generic
Hiya, I am really glad I have found this information. Nowadays bloggers publish just about gossips and net and this is really irritating. A good blog with interesting content, that is what I need. Thank you for keeping this website, I’ll be visiting it. Do you do newsletters? Can’t find it.
order azithromycin pills azithromycin 250mg brand zithromax 250mg for sale
gabapentin 800mg uk buy gabapentin medication
hello!,I like your writing so so much! share we be in contact more about your post on AOL? I need a specialist on this house to resolve my problem. Maybe that is you! Having a look ahead to look you.
oral azipro oral azipro 500mg order generic azithromycin 250mg
order lasix 40mg generic order lasix online
buy prednisolone tablets order omnacortil 40mg without prescription generic omnacortil 20mg
buy generic deltasone 5mg order prednisone 40mg online cheap
purchase amoxicillin online cheap cheap amoxil pill amoxicillin order online
purchase vibra-tabs online doxycycline 200mg cheap
ventolin usa order ventolin online ventolin inhalator online
amoxiclav online augmentin 1000mg generic
synthroid canada buy levothroid online cheap levoxyl buy online
levitra 20mg brand vardenafil 10mg us
clomiphene 100mg sale how to get clomiphene without a prescription order serophene generic
zanaflex cost order tizanidine 2mg online order tizanidine pills
order rybelsus 14mg pill how to get semaglutide without a prescription rybelsus 14 mg without prescription
buy prednisone 5mg online order deltasone 40mg pill order prednisone 5mg pills
order rybelsus 14mg pill rybelsus 14mg uk buy rybelsus 14 mg pills
buy generic accutane 20mg buy isotretinoin 40mg generic generic accutane
buy albuterol pill buy albuterol pill order albuterol online
buy amoxil sale order amoxicillin 1000mg generic buy amoxicillin 250mg
augmentin cheap amoxiclav price amoxiclav uk
zithromax 500mg without prescription order azithromycin 500mg online azithromycin 500mg usa
order synthroid 100mcg without prescription buy synthroid synthroid 150mcg brand
brand omnacortil 40mg order omnacortil 10mg online cheap buy omnacortil paypal
buy clomid 100mg generic buy serophene sale clomid for sale online
neurontin without prescription neurontin online buy order gabapentin 600mg online
furosemide 100mg uk order generic furosemide 100mg furosemide 40mg ca
sildenafil 100mg tablet free shipping viagra purchase viagra
Tadalafilo Pensa 10 Mg Precio
(Moderator)
Cialis 5 mg prezzo tadalafil 5 mg prezzo tadalafil 5 mg prezzo
This web site is really a walk-through for all of the info you wanted about this and didn’t know who to ask. Glimpse here, and you’ll definitely discover it.
purchase acticlate pill buy doxycycline cheap purchase monodox
rybelsus 14 mg usa order semaglutide 14mg generic purchase semaglutide generic
With almost everything that appears to be developing within this subject material, many of your points of view happen to be quite radical. Nevertheless, I beg your pardon, because I do not subscribe to your whole plan, all be it exciting none the less. It would seem to us that your comments are generally not completely justified and in simple fact you are your self not really completely certain of the point. In any case I did enjoy reading it.
vegas casino online blackjack card game casino slot free
purchase vardenafil pills order vardenafil 10mg for sale buy levitra without a prescription
buy generic pregabalin cheap pregabalin 75mg buy pregabalin pills for sale
buy generic hydroxychloroquine 200mg buy hydroxychloroquine pill hydroxychloroquine pills
purchase aristocort without prescription buy generic triamcinolone for sale order aristocort 4mg generic
Hello, its fastidious article on the topic of media print, we all be familiar with media is a impressive source of data.
https://secure.squirtingvirgin.com/track/MzAxODgyLjUuMjguMjguMC4wLjAuMC4w
order cialis 10mg cialis next day delivery usa cost cialis 5mg
Admiring the time and energy you put into your blog and detailed information you provide. It’s nice to come across a blog every once in a while that isn’t the same unwanted rehashed information. Wonderful read! I’ve saved your site and I’m adding your RSS feeds to my Google account.
cloudbet countries
buy clarinex paypal order desloratadine 5mg pills buy generic desloratadine online
buy cenforce 100mg online buy cenforce 100mg online order generic cenforce 100mg
loratadine price cost claritin claritin for sale online
generic chloroquine 250mg chloroquine 250mg sale aralen 250mg generic
dapoxetine us dapoxetine 90mg us order misoprostol pill
glucophage 1000mg sale buy glucophage 1000mg pill order generic metformin 500mg
zeolite heavy equipment llc is a trusted provider of heavy equipment, offering a diverse range of machines and devices for various industries. We strive to meet the needs of our customers by providing them with reliable solutions and excellent service. Our company is dedicated to helping our customers succeed in their business ventures.
xenical 120mg usa purchase orlistat sale generic diltiazem
Its like you read my mind! You seem to know so much about this, like you wrote the book in it or something. I think that you could do with some pics to drive the message home a bit, but other than that, this is excellent blog. An excellent read. I will certainly be back.
instant payid pokies australia
Aviator Spribe казино играть на доллары
Between us speaking, I advise to you to try to look in google.com
Добро пожаловать в захватывающий мир авиаторов! Aviator – это увлекательная игра, которая позволит вам окунуться в атмосферу боевых действий на небе. Необычные графика и захватывающий сюжет сделают ваше путешествие по воздуху неповторимым.
Откройте для себя новые возможности с игрой Aviator Spribe казино играть прямо сейчас!
Aviator игра позволит вам почувствовать себя настоящим пилотом. Вам предстоит совершить невероятные маневры, выполнять сложные задания и сражаться с противниками. Улучшайте свой самолет, чтобы быть готовым к любым ситуациям и становиться настоящим мастером.
Основные особенности Aviator краш игры:
1. Реалистичная графика и физика – благодаря передовой графике и реалистичной физике вы почувствуете себя настоящим пилотом.
2. Разнообразные режимы игры и миссии – в Aviator краш игре вы сможете выбрать различные режимы игры, такие как гонки, симулятор полетов и захватывающие воздушные бои. Кроме того, каждая миссия будет предлагать свои собственные вызовы и задачи.
3. Улучшение и модернизация самолетов – в игре доступны различные модели самолетов, которые можно покупать и улучшать. Вы сможете устанавливать новое оборудование, улучшать двигательность и мощность своего самолета, а также выбирать различные варианты окраски и декорации.
Aviator краш игра – это возможность испытать себя в роли авиатора и преодолеть все сложности и опасности воздушного пространства. Почувствуйте настоящую свободу и адреналин в Aviator краш игре онлайн!
Играйте в «Авиатор» в онлайн-казино Pin-Up
Aviator краш игра онлайн предлагает увлекательную и захватывающую игровую атмосферу, где вы становитесь настоящим авиатором и сражаетесь с самыми опасными искусственными интеллектами.
В этой игре вы должны показать свое мастерство и смекалку, чтобы преодолеть сложности многочисленных локаций и уровней. Вам предстоит собирать бонусы, уклоняться от препятствий и сражаться с врагами, используя свои навыки пилотирования и стрельбы.
Каждый уровень игры Aviator краш имеет свою уникальную атмосферу и задачи. Будьте готовы к неожиданностям, так как вас ждут захватывающие повороты сюжета и сложные испытания. Найдите все пути к победе и станьте настоящим героем авиатором!
Авиатор игра является прекрасным способом провести время и испытать настоящий адреналиновый разряд. Готовы ли вы стать лучшим авиатором? Не упустите свой шанс и начните играть в Aviator краш прямо сейчас!
Aviator – играй, сражайся, побеждай!
Aviator Pin Up (Авиатор Пин Ап ) – игра на деньги онлайн Казахстан
Aviator игра предлагает увлекательное и захватывающее разнообразие врагов и уровней, которые не оставят равнодушными даже самых требовательных геймеров.
Враги в Aviator краш игре онлайн представлены в самых разных формах и размерах. Здесь вы встретите группы из маленьких и быстрых врагов, а также огромных боссов с мощным вооружением. Разнообразие врагов позволяет игрокам использовать разные тактики и стратегии для победы.
Кроме того, Aviator игра предлагает разнообразие уровней сложности. Выберите легкий уровень, чтобы насладиться игровым процессом, или вызовите себе настоящий вызов, выбрав экспертный уровень. Независимо от выбранного уровня сложности, вы получите максимум удовольствия от игры и окунетесь в захватывающий мир авиаторов.
Играйте в Aviator и наслаждайтесь разнообразием врагов и уровней, которые позволят вам почувствовать себя настоящим авиатором.
buy lipitor sale lipitor 40mg over the counter lipitor 80mg usa
buy acyclovir 400mg without prescription zyloprim price cheap zyloprim 100mg
norvasc 10mg over the counter buy norvasc paypal purchase amlodipine online
lisinopril 5mg generic buy lisinopril 10mg order prinivil online cheap
rosuvastatin 10mg for sale buy zetia 10mg online cheap order zetia sale
order prilosec 20mg online omeprazole medication omeprazole price
buy cheap generic motilium motilium 10mg over the counter tetracycline 500mg oral
order metoprolol 50mg pills brand metoprolol lopressor pill
buy flexeril no prescription cyclobenzaprine medication order baclofen pill
When I initially commented I clicked the “Notify me when new comments are added” checkbox and now each time a comment is added I get three e-mails with the same comment. Is there any way you can remove people from that service? Bless you!
tenormin sale atenolol oral order tenormin 50mg pills
cost toradol toradol online colcrys us
cost of medrol buy medrol 4 mg online buy oral medrol
Ваш надежный партнер Пункт приема Металла в Алматы Наша компания предлагает высококачественные услуги по приему, сортировке и переработке металлических отходов. Мы гарантируем прозрачные условия сотрудничества, конкурентоспособные цены и оперативное обслуживание.
help with term paper college essay writing help pay for assignment
inderal 20mg usa cheap inderal 20mg clopidogrel 150mg drug
buy methotrexate cheap coumadin 2mg for sale warfarin 5mg without prescription
meloxicam usa order mobic 15mg pills celebrex 200mg drug
cost reglan 20mg buy reglan 20mg pill buy hyzaar for sale
tamsulosin 0.4mg pill buy tamsulosin without a prescription celecoxib over the counter
nexium drug purchase nexium online topamax canada
buy ondansetron 4mg online where can i buy aldactone buy aldactone without prescription
sumatriptan 25mg uk buy levaquin pill cost levaquin
buy simvastatin pill zocor online valacyclovir buy online
order dutasteride generic order zantac 150mg buy ranitidine generic
generic ampicillin ampicillin over the counter cheap amoxicillin pill
finpecia online order finasteride 5mg us buy fluconazole 200mg pill
order ciprofloxacin generic – buy generic myambutol for sale augmentin 375mg for sale
where can i buy baycip – ethambutol canada buy amoxiclav without prescription
What a stuff of un-ambiguity and preserveness of valuable familiarity on the topic of unexpected feelings.
http://images.google.cm/url?q=https://didvirtualnumbers.com/tr/
Thanks for another wonderful post. Where else may anybody get that kind of information in such an ideal approach of writing? I have a presentation subsequent week, and I’m on the look for such information.
https://www.google.nu/url?q=https://didvirtualnumbers.com/tr/
metronidazole usa – purchase zithromax for sale azithromycin for sale online
order ciplox 500mg generic – generic tindamax 500mg erythromycin 500mg cost
how to get valtrex without a prescription – order vermox pill order zovirax pills
ivermectin 6mg without a doctor prescription – buy ciplox 500 mg sumycin drug
Great paintings! This is the kind of information that are supposed to be shared across the internet. Shame on Google for no longer positioning this post higher! Come on over and seek advice from my website . Thanks =)
brand flagyl 200mg – buy cleocin medication buy azithromycin for sale
buy furosemide sale diuretic – buy prazosin 1mg generic buy capoten 25mg pill
order zidovudine 300 mg sale – cost allopurinol 100mg buy allopurinol 100mg pill
buy glucophage generic – metformin 1000mg for sale buy lincomycin 500 mg generic
Authorities say it will protect the city and ensure stability, while critics are alarmed it will silence all dissent with its closed-door trials and life sentences for broadly-defined제천출장안마 offences – from insurrection to treason.
clozaril pills – ramipril generic famotidine 40mg ca
purchase quetiapine online cheap – ziprasidone 80mg price purchase eskalith generic
atarax 10mg ca – order buspar 5mg for sale amitriptyline online order
oral clomipramine – amoxapine medication sinequan 25mg drug
amoxicillin medication – purchase cefadroxil generic cipro uk
order augmentin 1000mg online – baycip ca order ciprofloxacin 500mg without prescription
buy cheap generic cleocin – order chloramphenicol without prescription chloromycetin canada
buy zithromax 250mg online cheap – how to get tinidazole without a prescription ciplox 500 mg usa
albuterol inhalator online – buy theo-24 Cr 400 mg online cheap theo-24 Cr for sale
ivermectin human – order eryc 500mg sale order cefaclor 250mg online cheap
Saved as a favorite, I really like your blog!
desloratadine oral – desloratadine 5mg brand buy albuterol generic
An interesting discussion is worth comment. I think that you should write more on this topic, it might not be a taboo subject but generally people are not enough to speak on such topics. To the next. Cheers
medrol 8mg tablet – methylprednisolone 4 mg online generic azelastine 10ml
buy micronase 5mg online – glyburide drug buy dapagliflozin cheap
buy repaglinide 2mg pills – jardiance sale buy empagliflozin 10mg sale
You have brought up a very superb details, thankyou for the post.
buy glucophage cheap – hyzaar online order acarbose 25mg usa
PBN sites
We establish a system of self-owned blog network sites!
Benefits of our private blog network:
We execute everything SO THAT GOOGLE DOES NOT comprehend that this is A PBN network!!!
1- We buy domain names from distinct registrars
2- The leading site is hosted on a VPS hosting (VPS is rapid hosting)
3- The rest of the sites are on separate hostings
4- We assign a separate Google ID to each site with confirmation in Search Console.
5- We make websites on WordPress, we don’t use plugins with aided by which malware penetrate and through which pages on your websites are established.
6- We refrain from repeat templates and employ only unique text and pictures
We refrain from work with website design; the client, if wanted, can then edit the websites to suit his wishes
Its fantastic as your other articles : D, regards for putting up.
terbinafine for sale online – griseofulvin generic griseofulvin canada
buy generic rybelsus 14mg – oral rybelsus desmopressin generic
buy nizoral – ketoconazole 200mg canada buy itraconazole cheap
Understanding COSC Certification and Its Importance in Horology
COSC Certification and its Stringent Standards
Controle Officiel Suisse des Chronometres, or the Official Swiss Chronometer Testing Agency, is the authorized Switzerland testing agency that attests to the precision and accuracy of wristwatches. COSC certification is a mark of excellent craftsmanship and trustworthiness in chronometry. Not all timepiece brands seek COSC certification, such as Hublot, which instead sticks to its proprietary demanding standards with movements like the UNICO calibre, reaching similar precision.
The Science of Precision Chronometry
The core mechanism of a mechanized watch involves the mainspring, which supplies power as it unwinds. This system, however, can be prone to environmental factors that may impact its accuracy. COSC-certified mechanisms undergo demanding testing—over 15 days in various circumstances (five positions, 3 temperatures)—to ensure their durability and dependability. The tests evaluate:
Average daily rate precision between -4 and +6 seconds.
Mean variation, highest variation rates, and impacts of thermal variations.
Why COSC Accreditation Is Important
For watch fans and connoisseurs, a COSC-certified watch isn’t just a piece of tech but a testament to lasting excellence and accuracy. It signifies a timepiece that:
Provides exceptional reliability and precision.
Provides guarantee of quality across the complete construction of the watch.
Is apt to retain its worth better, making it a wise investment.
Popular Chronometer Brands
Several well-known brands prioritize COSC validation for their watches, including Rolex, Omega, Breitling, and Longines, among others. Longines, for instance, offers collections like the Archive and Spirit, which showcase COSC-accredited mechanisms equipped with cutting-edge materials like silicone equilibrium springs to boost resilience and efficiency.
Historic Background and the Evolution of Chronometers
The idea of the chronometer dates back to the requirement for precise chronometry for navigation at sea, highlighted by John Harrison’s work in the 18th cent. Since the official establishment of COSC in 1973, the validation has become a standard for evaluating the precision of high-end watches, sustaining a legacy of excellence in horology.
Conclusion
Owning a COSC-validated timepiece is more than an visual selection; it’s a dedication to excellence and accuracy. For those appreciating accuracy above all, the COSC accreditation offers peacefulness of mind, ensuring that each accredited watch will operate reliably under various conditions. Whether for individual satisfaction or as an investment, COSC-validated timepieces distinguish themselves in the world of watchmaking, maintaining on a tradition of precise timekeeping.
purchase lanoxin generic – trandate 100mg drug lasix generic
This site is my inhalation, rattling good style and perfect articles.
En Son Dönemin En Büyük Popüler Kumarhane Sitesi: Casibom
Kumarhane oyunlarını sevenlerin artık duymuş olduğu Casibom, en son dönemde adından çoğunlukla söz ettiren bir bahis ve kumarhane web sitesi haline geldi. Ülkemizdeki en mükemmel bahis platformlardan biri olarak tanınan Casibom’un haftalık bazda göre değişen açılış adresi, piyasada oldukça taze olmasına rağmen emin ve kar getiren bir platform olarak öne çıkıyor.
Casibom, muadillerini geride kalarak eski bahis web sitelerinin önüne geçmeyi başarılı oluyor. Bu pazarda köklü olmak gereklidir olsa da, katılımcılarla iletişimde bulunmak ve onlara temasa geçmek da aynı kadar değerli. Bu noktada, Casibom’un 7/24 hizmet veren gerçek zamanlı destek ekibi ile rahatça iletişime geçilebilir olması büyük önem taşıyan bir avantaj getiriyor.
Hızla genişleyen oyuncuların kitlesi ile dikkat çekici olan Casibom’un gerisindeki başarım faktörleri arasında, sadece casino ve canlı casino oyunları ile sınırlı olmayan geniş bir hizmetler yelpazesi bulunuyor. Spor bahislerinde sunduğu geniş alternatifler ve yüksek oranlar, oyuncuları çekmeyi başarıyor.
Ayrıca, hem spor bahisleri hem de kumarhane oyunlar oyuncularına yönelik sunulan yüksek yüzdeli avantajlı promosyonlar da ilgi çekici. Bu nedenle, Casibom hızla piyasada iyi bir tanıtım başarısı elde ediyor ve büyük bir oyuncuların kitlesi kazanıyor.
Casibom’un kazandıran promosyonları ve popülerliği ile birlikte, platforma üyelik ne şekilde sağlanır sorusuna da atıfta bulunmak gerekir. Casibom’a mobil cihazlarınızdan, PC’lerinizden veya tabletlerinizden web tarayıcı üzerinden rahatça ulaşılabilir. Ayrıca, sitenin mobil cihazlarla uyumlu olması da önemli bir avantaj sağlıyor, çünkü şimdi neredeyse herkesin bir akıllı telefonu var ve bu akıllı telefonlar üzerinden kolayca erişim sağlanabiliyor.
Hareketli tabletlerinizle bile yolda gerçek zamanlı tahminler alabilir ve müsabakaları canlı olarak izleyebilirsiniz. Ayrıca, Casibom’un mobil uyumlu olması, memleketimizde kumarhane ve casino gibi yerlerin kanuni olarak kapatılmasıyla birlikte bu tür platformlara erişimin büyük bir yolunu oluşturuyor.
Casibom’un itimat edilir bir kumarhane sitesi olması da gereklidir bir artı sağlıyor. Ruhsatlı bir platform olan Casibom, sürekli bir şekilde keyif ve kazanç elde etme imkanı sağlar.
Casibom’a abone olmak da oldukça rahatlatıcıdır. Herhangi bir belge şartı olmadan ve bedel ödemeden web sitesine kolaylıkla abone olabilirsiniz. Ayrıca, platform üzerinde para yatırma ve çekme işlemleri için de çok sayıda farklı yöntem vardır ve herhangi bir kesim ücreti isteseniz de alınmaz.
Ancak, Casibom’un güncel giriş adresini takip etmek de gereklidir. Çünkü canlı bahis ve casino siteleri moda olduğu için sahte siteler ve dolandırıcılar da ortaya çıkmaktadır. Bu nedenle, Casibom’un sosyal medya hesaplarını ve güncel giriş adresini düzenli aralıklarla kontrol etmek önemlidir.
Sonuç, Casibom hem emin hem de kazanç sağlayan bir casino web sitesi olarak ilgi çekiyor. Yüksek ödülleri, geniş oyun seçenekleri ve kullanıcı dostu taşınabilir uygulaması ile Casibom, oyun hayranları için ideal bir platform sağlar.
order famciclovir 500mg generic – buy famvir 500mg generic valcivir online
로드스탁과 레버리지 방식의 스탁: 투자의 새로운 분야
로드스탁에서 제공하는 레버리지 스탁은 주식 투자의 한 방법으로, 높은 이익율을 목적으로 하는 투자자들에게 매력적인 선택입니다. 레버리지 사용을 사용하는 이 방법은 투자자가 자신의 투자금을 초과하는 투자금을 투자할 수 있도록 함으로써, 증권 시장에서 더 큰 작용을 가질 수 있는 기회를 제공합니다.
레버리지 스탁의 기본 원칙
레버리지 스탁은 원칙적으로 자본을 빌려 운용하는 방식입니다. 예를 들어, 100만 원의 자금으로 1,000만 원 상당의 증권을 취득할 수 있는데, 이는 투자자가 기본 투자 금액보다 훨씬 더 많은 주식을 구매하여, 증권 가격이 증가할 경우 관련된 훨씬 더 큰 이익을 가져올 수 있게 해줍니다. 그렇지만, 증권 값이 내려갈 경우에는 그 피해 또한 커질 수 있으므로, 레버리지를 이용할 때는 신중하게 생각해야 합니다.
투자 전략과 레버리지
레버리지 사용은 특히 성장 가능성이 큰 사업체에 적용할 때 효과적입니다. 이러한 기업에 상당한 비율로 적용하면, 잘 될 경우 막대한 수익을 가져올 수 있지만, 반대 경우의 경우 큰 리스크도 감수하게 됩니다. 그러므로, 투자하는 사람은 자신의 리스크 관리 능력과 시장 분석을 통해 통해, 일정한 회사에 얼마만큼의 자금을 적용할지 결정하게 됩니다 합니다.
레버리지의 이점과 위험성
레버리지 방식의 스탁은 상당한 수익을 보장하지만, 그만큼 상당한 위험성 동반합니다. 증권 시장의 변동은 예측이 어렵기 때문에, 레버리지 사용을 사용할 때는 언제나 상장 경향을 정밀하게 주시하고, 피해를 최소로 줄일 수 있는 전략을 구성해야 합니다.
결론: 조심스러운 결정이 필수입니다
로드스탁에서 공급하는 레버리지 방식의 스탁은 효과적인 투자 도구이며, 적절히 활용하면 큰 이익을 벌어들일 수 있습니다. 하지만 높은 리스크도 생각해 봐야 하며, 투자 선택은 충분히 많은 정보와 조심스러운 고려 후에 실시되어야 합니다. 투자자 자신의 재정적 상태, 리스크 감수 능력, 그리고 시장 상황을 생각한 균형 잡힌 투자 계획이 핵심입니다.
buy hydrochlorothiazide 25mg generic – amlodipine cost purchase bisoprolol for sale
проверить свои usdt на чистоту
Проверка кошельков кошельков для хранения криптовалюты на наличие нелегальных денег: Защита личного электронного портфеля
В мире электронных денег становится все необходимее обеспечивать секретность личных денег. Каждый день кибермошенники и злоумышленники выработывают совершенно новые методы мошенничества и кражи электронных финансов. Ключевым инструментом важных инструментов защиты является проверка кошельков на выявление наличия неправомерных средств.
Почему так важно осмотреть личные криптовалютные бумажники?
В первую очередь данный факт важно для того, чтобы обеспечения безопасности собственных средств. Многие участники рынка рискуют потерять утраты своих собственных средств вследствие недоброжелательных методов или угонов. Анализ кошельков способствует предотвращению выявить вовремя сомнительные операции и предотвратить возможные.
Что предлагает фирма?
Мы оказываем услугу проверки цифровых бумажников и транзакций средств с целью обнаружения источника средств и выдачи подробного отчета о результатах. Наши программа осматривает данные для выявления неправомерных действий и определить уровень риска для того чтобы личного финансового портфеля. Благодаря нашей службе проверки, вы будете в состоянии предотвратить с регуляторами и защитить от случайного участия в финансировании незаконных деятельностей.
Как проводится процесс проверки?
Организация наша компания взаимодействует с ведущими аудиторами структурами, например Halborn, для того чтобы дать гарантию и точность наших анализов. Мы внедряем передовые и техники проверки данных для обнаружения опасных операций. Данные пользователей наших пользователей обрабатываются и хранятся согласно высокими требованиями.
Основная просьба: “проверить свои USDT на чистоту”
В случае если вы хотите убедиться надежности своих USDT-кошельков, наша компания предоставляет возможность исследовать бесплатный анализ первых пяти кошельков. Просто введите свой кошелек в соответствующее поле на нашем сайте проверки, и мы вышлем вам подробный отчет о его статусе.
Обеспечьте защиту своих активы в данный момент!
Не рискуйте оказаться в пострадать от злоумышленников или стать неприятной ситуации из-за незаконных операций средств с ваших деньгами. Дайте вашу криптовалюту профессионалам, которые окажут поддержку, вам и вашим деньгам обезопаситься криптовалютные средства и избежать. Примите первый шаг к защите безопасности личного криптовалютного портфельчика уже сегодня!
Тестирование Tether на чистоту: Как обезопасить свои электронные состояния
Все более пользователей заботятся в безопасность собственных криптовалютных активов. День ото дня обманщики придумывают новые методы разграбления цифровых средств, а также владельцы криптовалюты оказываются страдающими их интриг. Один из способов защиты становится проверка кошельков в наличие нелегальных финансов.
Для чего это полезно?
Преимущественно, чтобы обезопасить личные средства от обманщиков и похищенных денег. Многие инвесторы сталкиваются с риском потери личных средств вследствие мошеннических планов либо кражей. Тестирование кошельков способствует определить подозрительные действия и предотвратить потенциальные убытки.
Что наша команда предлагаем?
Мы предлагаем подход тестирования цифровых бумажников а также операций для обнаружения происхождения средств. Наша система анализирует информацию для выявления противозаконных операций или оценки риска для вашего счета. Благодаря данной проверке, вы сможете избегать проблем с регулированием или предохранить себя от участия в противозаконных операциях.
Как происходит процесс?
Наша команда сотрудничаем с первоклассными проверочными организациями, наподобие Certik, для того чтобы обеспечить аккуратность наших тестирований. Мы применяем современные технологии для выявления потенциально опасных операций. Ваши информация проходят обработку и хранятся в соответствии с высокими стандартами безопасности и конфиденциальности.
Как проверить свои Tether в чистоту?
Если вам нужно подтвердить, что ваши USDT-кошельки чисты, наш сервис предлагает бесплатное тестирование первых пяти кошельков. Легко вбейте адрес вашего кошелька в нашем сайте, а также наша команда предоставим вам детальный отчет о его положении.
Гарантируйте безопасность для ваши активы уже сейчас!
Не рискуйте подвергнуться мошенников или попасть в неприятную ситуацию из-за незаконных операций. Обратитесь к нашей команде, для того чтобы сохранить ваши криптовалютные активы и предотвратить проблем. Сделайте первый шаг к сохранности вашего криптовалютного портфеля уже сейчас!
order lopressor 50mg pills – buy cozaar online order nifedipine pill
There is noticeably a bunch to know about this. I suppose you made various good points in features also.
Анализ бумажников за выявление наличия нелегальных средств: Обеспечение безопасности своего цифрового портфельчика
В мире цифровых валют становится все важнее важнее гарантировать защиту своих финансов. Постоянно жулики и киберпреступники выработывают свежие схемы обмана и мошенничества и воровства цифровых средств. Одним из существенных методов обеспечения безопасности является проверка бумажников по выявление неправомерных средств.
Почему именно поэтому важно провести проверку свои электронные бумажники?
В первую очередь, вот это необходимо для того, чтобы защиты личных финансовых средств. Многие инвесторы рискуют потери денег своих финансов из-за непорядочных подходов или краж. Проверка кошельков бумажников способствует своевременно выявить подозрительные операции и предотвратить возможные.
Что предлагает вашему вниманию наша компания?
Мы предоставляем послугу проверки кошельков цифровых кошельков и транзакций с намерением идентификации места происхождения финансовых средств и дать полного доклада. Наши программа анализирует информацию для идентификации потенциально нелегальных манипуляций и оценить риск для того, чтобы своего финансового портфеля. Благодаря нашей системе проверки, вы будете способны избежать с органами контроля и обезопасить от случайного участия в незаконных операций.
Как проводится процесс?
Организация наша фирма сотрудничает с известными аудиторскими организациями структурами, как например Cure53, для того чтобы дать гарантию и точность наших проверок данных. Мы внедряем передовые и подходы анализа для идентификации опасных манипуляций. Личные данные наших заказчиков обрабатываются и хранятся в базе согласно высокими стандартами.
Основная просьба: “проверить свои USDT на чистоту”
Если вас интересует убедиться безопасности собственных USDT-кошельков, наши эксперты предлагает возможность бесплатную проверку наших специалистов первых 5 кошельков. Просто введите свой кошелек в соответствующее поле на нашем сайте проверки, и мы вышлем вам подробные сведения о состоянии вашего счета.
Обеспечьте защиту своих финансовые активы прямо сейчас!
Избегайте риска оказаться в жертвой хакеров или попасть неприятном положении неправомерных действий с ваших финансами. Позвольте себе специалистам, которые окажут помощь, вам и вашим деньгам обезопасить деньги и предотвратить возможные. Примите первый шаг к защите обеспечению безопасности вашего цифрового портфеля активов уже сегодня!
чистый usdt
Осмотр Тетер в прозрачность: Каким образом обезопасить свои криптовалютные активы
Каждый день все больше граждан заботятся для безопасность личных криптовалютных активов. День ото дня шарлатаны предлагают новые подходы кражи криптовалютных средств, а также собственники криптовалюты становятся жертвами своих подстав. Один методов сбережения становится проверка кошельков для наличие незаконных средств.
С какой целью это необходимо?
Прежде всего, чтобы защитить свои средства против мошенников а также похищенных монет. Многие участники встречаются с потенциальной угрозой потери их активов из-за мошеннических сценариев или краж. Анализ бумажников позволяет обнаружить подозрительные операции или предотвратить возможные убытки.
Что наша команда предоставляем?
Мы предоставляем услугу тестирования криптовалютных кошельков и также операций для определения источника средств. Наша технология исследует данные для определения незаконных транзакций а также проценки угрозы для вашего портфеля. Вследствие этой проверке, вы сможете избегать проблем с регуляторами и защитить себя от участия в незаконных сделках.
Как происходит процесс?
Мы сотрудничаем с лучшими аудиторскими агентствами, вроде Kudelsky Security, для того чтобы гарантировать аккуратность наших тестирований. Наша команда внедряем передовые техники для обнаружения потенциально опасных операций. Ваши данные обрабатываются и хранятся согласно с высокими нормами безопасности и конфиденциальности.
Как проверить личные USDT в чистоту?
Если хотите проверить, что ваши USDT-кошельки прозрачны, наш сервис предоставляет бесплатную проверку первых пяти бумажников. Просто введите место своего кошелька на на нашем веб-сайте, и также мы предоставим вам детальный доклад об его статусе.
Защитите свои фонды уже сегодня!
Не подвергайте риску подвергнуться мошенников или попасть в неприятную ситуацию по причине незаконных транзакций. Посетите нашему сервису, чтобы обезопасить свои криптовалютные средства и предотвратить проблем. Примите первый шаг к сохранности вашего криптовалютного портфеля уже сейчас!
грязный usdt
Осмотр Tether в чистоту: Каковым способом обезопасить собственные криптовалютные средства
Постоянно все больше людей заботятся для безопасность своих электронных активов. Ежедневно обманщики разрабатывают новые схемы разграбления электронных активов, а также держатели цифровой валюты оказываются пострадавшими своих подстав. Один техник охраны становится проверка кошельков на присутствие противозаконных средств.
Зачем это необходимо?
Прежде всего, для того чтобы защитить собственные финансы от шарлатанов и также украденных денег. Многие участники сталкиваются с вероятностью убытков своих активов из-за мошеннических сценариев либо хищений. Анализ кошельков помогает определить сомнительные операции или предотвратить возможные убытки.
Что наша группа предоставляем?
Мы предлагаем подход проверки электронных бумажников или операций для выявления источника средств. Наша система исследует данные для обнаружения противозаконных действий а также оценки угрозы для вашего портфеля. За счет этой проверке, вы сможете избегнуть проблем с регуляторами или защитить себя от участия в незаконных операциях.
Как происходит процесс?
Мы работаем с передовыми проверочными агентствами, например Halborn, чтобы обеспечить точность наших проверок. Мы применяем современные технологии для обнаружения опасных транзакций. Ваши информация обрабатываются и сохраняются согласно с высокими стандартами безопасности и приватности.
Как проверить собственные USDT в чистоту?
Если хотите проверить, что ваши Tether-бумажники чисты, наш подход предоставляет бесплатную проверку первых пяти кошельков. Просто передайте адрес собственного кошелька на на сайте, а также наш сервис предоставим вам детальный доклад о его положении.
Гарантируйте безопасность для вашими активы сегодня же!
Не подвергайте риску подвергнуться шарлатанов или оказаться в неприятную ситуацию по причине нелегальных сделок. Обратитесь к нашему агентству, чтобы сохранить ваши электронные средства и избежать сложностей. Предпримите первый шаг к безопасности вашего криптовалютного портфеля прямо сейчас!
order nitroglycerin for sale – buy lozol for sale buy diovan tablets
Проверка USDT на чистоту
Осмотр Тетер на чистоту: Каким образом сохранить личные цифровые активы
Каждый день все больше граждан обращают внимание к надежность их цифровых средств. Ежедневно дельцы изобретают новые схемы кражи цифровых средств, или владельцы криптовалюты становятся пострадавшими их афер. Один из техник сбережения становится проверка кошельков для присутствие противозаконных средств.
С какой целью это полезно?
Прежде всего, с тем чтобы обезопасить личные активы от дельцов а также похищенных денег. Многие участники сталкиваются с потенциальной угрозой потери личных фондов вследствие хищных схем или кражей. Осмотр кошельков позволяет выявить подозрительные операции а также предотвратить возможные потери.
Что наша команда предоставляем?
Наша компания предлагаем подход проверки электронных кошельков или транзакций для выявления происхождения фондов. Наша система анализирует данные для обнаружения нелегальных действий и также оценки риска вашего портфеля. За счет этой проверке, вы сможете избежать недочетов с регуляторами а также защитить себя от участия в незаконных переводах.
Как это действует?
Наша фирма сотрудничаем с первоклассными проверочными организациями, наподобие Cure53, для того чтобы обеспечить аккуратность наших проверок. Мы используем передовые технологии для выявления потенциально опасных транзакций. Ваши информация обрабатываются и сохраняются согласно с высокими нормами безопасности и приватности.
Как выявить свои USDT на чистоту?
В случае если вы желаете проверить, что ваша Tether-бумажники прозрачны, наш сервис предлагает бесплатную проверку первых пяти бумажников. Просто передайте положение вашего кошелька в нашем сайте, и наш сервис предоставим вам подробный отчет об его положении.
Гарантируйте безопасность для ваши фонды сегодня же!
Не подвергайте риску попасть в жертву дельцов либо оказаться в неприятную ситуацию по причине нелегальных сделок. Посетите нашей команде, с тем чтобы сохранить ваши цифровые активы и предотвратить неприятностей. Примите первый шаг к безопасности вашего криптовалютного портфеля уже сегодня!
Тетер – это неизменная криптовалютный актив, привязанная к национальной валюте, подобно USD. Данное обстоятельство позволяет данный актив в особенности популярной среди трейдеров, так как данный актив обеспечивает надежность курса в условиях волатильности криптовалютного рынка. Тем не менее, как и любая другая тип цифровых активов, USDT подвержена риску использования с целью отмывания денег и финансирования неправомерных сделок.
Отмывание денег путем цифровые валюты переходит в все более распространенным способом для того чтобы скрытия происхождения средств. Используя разнообразные техники, мошенники могут стараться легализовывать незаконно завоеванные средства путем криптовалютные обменники или миксеры, для того чтобы совершить их происхождение менее прозрачным.
Именно для этой цели, проверка USDT на чистоту оказывается весьма существенной практикой предосторожности для пользователей криптовалют. Существуют специализированные услуги, которые осуществляют проверку сделок и бумажников, для того чтобы идентифицировать подозрительные операции и противоправные финансирование. Данные услуги способствуют участникам избежать непреднамеренной участи в преступных действий и предотвратить блокировку аккаунтов со со стороны сторонних надзорных органов.
Экспертиза USDT на чистоту также предотвращает обезопасить себя от возможных финансовых убытков. Участники могут быть уверенны в том, что их активы не ассоциированы с противоправными операциями, что соответственно уменьшает вероятность блокировки счета или перечисления денег.
Таким образом, в условиях современности повышающейся сложности среды криптовалют требуется принимать действия для обеспечения безопасности и надежности своих активов. Анализ USDT на чистоту с использованием специальных платформ является важной одним из методов противодействия незаконной деятельности, обеспечивая владельцам цифровых валют дополнительную защиту и защиты.
https://rg777.app/cup-c1-202324/
Backlinks seo
Efficient Links in Blogs and Comments: Boost Your SEO
Backlinks are vital for improving search engine rankings and increasing site visibility. By incorporating backlinks into blogs and comments prudently, they can significantly enhance targeted traffic and SEO overall performance.
Adhering to Search Engine Algorithms
Today’s backlink placement tactics are finely tuned to align with search engine algorithms, which now prioritize link quality and significance. This ensures that hyperlinks are not just numerous but significant, guiding users to helpful and pertinent articles. Website owners should concentrate on integrating links that are contextually suitable and boost the overall articles good quality.
Advantages of Utilizing Refreshing Donor Bases
Making use of current contributor bases for hyperlinks, like those maintained by Alex, delivers considerable benefits. These bases are frequently renewed and consist of unmoderated websites that don’t pull in complaints, guaranteeing the hyperlinks positioned are both powerful and certified. This strategy helps in sustaining the effectiveness of hyperlinks without the pitfalls associated with moderated or problematic resources.
Only Approved Resources
All donor sites used are sanctioned, avoiding legal pitfalls and conforming to digital marketing standards. This determination to making use of only sanctioned resources assures that each backlink is genuine and trustworthy, thereby constructing trustworthiness and reliability in your digital presence.
SEO Impact
Expertly put backlinks in weblogs and comments provide over just SEO rewards—they enhance user encounter by linking to appropriate and top quality articles. This strategy not only satisfies search engine conditions but also engages users, leading to far better visitors and enhanced online proposal.
In essence, the right backlink strategy, specifically one that utilizes refreshing and reliable donor bases like Alex’s, can change your SEO efforts. By focusing on quality over amount and adhering to the most recent standards, you can make sure your backlinks are both powerful and efficient.
usdt не чистое
Проверка Tether в чистоту: Каковым способом сохранить личные цифровые средства
Все больше пользователей обращают внимание к безопасность личных криптовалютных активов. Постоянно дельцы предлагают новые подходы разграбления цифровых средств, а также владельцы криптовалюты оказываются жертвами их обманов. Один из способов охраны становится проверка кошельков на наличие противозаконных финансов.
Для чего это потребуется?
В первую очередь, с тем чтобы обезопасить свои финансы против шарлатанов или украденных монет. Многие участники сталкиваются с вероятностью потери личных активов по причине обманных планов или грабежей. Осмотр кошельков помогает обнаружить сомнительные действия и предотвратить потенциальные потери.
Что наша команда предоставляем?
Мы предоставляем услугу проверки криптовалютных кошельков а также операций для выявления источника средств. Наша система анализирует информацию для определения нелегальных операций или оценки риска вашего портфеля. Вследствие этой проверке, вы сможете избежать недочетов с регуляторами и также защитить себя от участия в противозаконных операциях.
Как это работает?
Наша фирма сотрудничаем с ведущими проверочными компаниями, например Certik, для того чтобы предоставить аккуратность наших проверок. Наша команда применяем передовые техники для выявления потенциально опасных транзакций. Ваши информация проходят обработку и хранятся согласно с высокими стандартами безопасности и конфиденциальности.
Как проверить свои Tether для прозрачность?
При наличии желания проверить, что ваши USDT-кошельки чисты, наш сервис предоставляет бесплатное тестирование первых пяти кошельков. Просто вбейте адрес вашего кошелька в на нашем веб-сайте, или наш сервис предложим вам подробный отчет о его положении.
Гарантируйте безопасность для вашими средства уже сегодня!
Не подвергайте риску подвергнуться обманщиков либо попасть в неблагоприятную обстановку по причине незаконных операций. Посетите нашему агентству, для того чтобы сохранить ваши электронные активы и предотвратить затруднений. Совершите первый шаг к безопасности вашего криптовалютного портфеля прямо сейчас!
Backlinks seo
Effective Links in Blogs and forums and Remarks: Increase Your SEO
Links are essential for improving search engine rankings and enhancing website presence. By incorporating hyperlinks into weblogs and remarks prudently, they can significantly enhance targeted traffic and SEO overall performance.
Adhering to Search Engine Algorithms
The current day’s backlink placement methods are finely tuned to align with search engine algorithms, which now emphasize website link good quality and relevance. This assures that hyperlinks are not just abundant but meaningful, guiding consumers to beneficial and pertinent content. Site owners should emphasis on incorporating backlinks that are contextually proper and boost the overall articles high quality.
Advantages of Making use of Refreshing Donor Bases
Utilizing up-to-date contributor bases for backlinks, like those maintained by Alex, offers significant benefits. These bases are often renewed and consist of unmoderated websites that don’t attract complaints, guaranteeing the hyperlinks placed are both impactful and agreeable. This strategy assists in sustaining the effectiveness of backlinks without the risks associated with moderated or problematic resources.
Only Authorized Resources
All donor sites used are sanctioned, steering clear of legal pitfalls and sticking to digital marketing standards. This dedication to making use of only sanctioned resources assures that each backlink is genuine and trustworthy, thus developing credibility and reliability in your digital presence.
SEO Impact
Expertly positioned backlinks in weblogs and comments provide more than just SEO advantages—they improve user encounter by connecting to pertinent and high-quality articles. This strategy not only fulfills search engine requirements but also entails consumers, leading to far better targeted traffic and improved online proposal.
In essence, the right backlink strategy, especially one that utilizes refreshing and reliable donor bases like Alex’s, can change your SEO efforts. By concentrating on quality over quantity and adhering to the most recent standards, you can make sure your backlinks are both potent and efficient.
קנאביס מדריך: המדריכים המקיף לסחר שרף באמצעות המשלוח
טלגראס מדריך הם פורטל ידע ומדריכי להשקיה שרף במקום היישומון הפופולרית המשלוח.
האתר מספקת את כלל המידע הקישורים לאתרים והמסמכים העדכוני לקבוצות המשתמשים וערוצים המומלצים מומלצים לביקור לסחר ב שרף בטלגרם בארץ ישראל.
כמו למעשה, פורטל מספק מדריך מפורטת לכיצד ניתן להתכנן בהשרף ולקנות פרחי קנאביס בקלות ובמהירות.
בעזרת ההוראות, אף משתמשים חדשים בתחום יוכלו להירשם להמערכת ההפרח בהמשלוח בפני בטוחה ומאובטחת לשימוש.
ההאוטומטיזציה של טלגראס מאפשר למשתמשים ללהוציא פעולות השונות שונות וצבעוניות כגון הזמנת פרחי קנאביס, קבלת סיוע, בדיקת והוספת פידבק על המצרים. כל זאת בצורה נוחה לשימוש ופשוטה דרך היישומון.
כאשר כאשר נדבר בשיטות ה שלמות, טלגראס מנהלת באמצעים מוכרות כמו גם כסף מזומן, כרטיסי אשראי ומטבע דיגיטלי. חיוני להדגש כי יש לבדוק ולוודא את ההוראות והחוקים האזוריים בארץ שלך ללפני התבצעות רכישה.
הטלגרמה מציע הטבות מרכזיים כגון הגנת הפרטיות והגנה מוגברים, השיחה מהירה וגמישות גבוהה. בנוסף, הוא מאפשר גישה להקהל גלובלית רחבה ומציע מגוון רחב של תכונות ויכולות.
בבתום, המסר הנחיות היה האתר האידיאלי ללמצוא את כל המידע והקישורות לסחר ב קנאביס בדרך מהירה, בבטוחה ונוחה דרך הטלגרמה.
קזינו אונליין
הימורים ברשת הם חוויות מרגשת ופופולרי ביותר בעידן המקוון, שמביאה מיליוני אנשים מכל
רחבי העולם. ההימורים המקוונים מתרחשים על אירועים ספורטיים, תוצאות פוליטיות ואפילו תוצאות מזג האוויר ונושאים נוספים. אתרים ל הימורים הווירטואליים מקריאים פוטנציאליים את המשתתפים להמר על תוצאות מתאימות וליהנות רגעים מרגשים ומהנים.
ההימורים המקוונים הם כבר חלק מתרבות החברה לא מעט זמן והיום הם כבר לא רק חלק נפרד מהפעילות הכלכלית והתרבותית, אלא גם מספקים רווחים וחוויים. משום שהם נגישים לכולם וקלים לשימוש, הם מובילים את כולם ליהנות מהמשחק ולהנציח רגעי עסקה וניצחון בכל זמן ובכל מקום.
טכנולוגיות דיגיטליות והימורים מקוונים הפכו להיות הפופולריים ביותר בין האהובות והנפוצות. מיליוני אנשים מכל רחבי העולם מעוניינים בהימורים, הכוללים הימורי ספורט. הימורים מקוונים מציעים למשתתפים חוויה מהנה ומרגשת, המתאימה לכולם בכל זמן ובכל מקום.
וכן מה חכם אתה מחכה? אל תהסס והצטרף עכשיו והתחיל לחוות את ההתרגשות וההנאה שהימורים מקוונים מציעים.
Sure, here’s the text with spin syntax applied:
Hyperlink Structure
After numerous updates to the G search algorithm, it is essential to employ different approaches for ranking.
Today there is a means to attract the interest of search engines to your site with the assistance of incoming links.
Backlinks are not only an powerful promotional tool but they also have organic traffic, direct sales from these sources probably will not be, but click-throughs will be, and it is beneficial visitors that we also receive.
What in the end we get at the final outcome:
We display search engines site through backlinks.
Prluuchayut natural click-throughs to the site and it is also a sign to search engines that the resource is used by people.
How we show search engines that the site is profitable:
Links do to the principal page where the main information.
We make links through redirections reputable sites.
The most CRUCIAL we place the site on sites analyzers separate tool, the site goes into the cache of these analyzers, then the acquired links we place as redirections on blogs, discussion boards, comments. This significant action shows search engines the site map as analyzer sites show all information about sites with all keywords and headings and it is very BENEFICIAL.
All details about our services is on the website!
rosuvastatin pills awake – ezetimibe spy caduet pills midst
link building
Backlink creation is merely just as efficient at present, simply the instruments to work within this domain possess changed.
There are many options regarding inbound links, we utilize a few of them, and these strategies function and have already been examined by us and our customers.
Not long ago we carried out an experiment and it turned out that low-volume queries from just one website position effectively in search results, and it doesnt need to be your own domain, you are able to make use of social media from Web 2.0 collection for this.
It is also possible to partly shift mass through website redirects, giving a varied link profile.
Visit to our web page where our own solutions are typically presented with thorough overview.
Creating exclusive articles on Medium and Telegraph, why it is necessary:
Created article on these resources is better ranked on less common queries, which is very important to get organic traffic.
We get:
organic traffic from search engines.
natural traffic from the inner rendition of the medium.
The platform to which the article refers gets a link that is profitable and increases the ranking of the site to which the article refers.
Articles can be made in any amount and choose all less common queries on your topic.
Medium pages are indexed by search engines very well.
Telegraph pages need to be indexed individually indexer and at the same time after indexing they sometimes occupy places higher in the search engines than the medium, these two platforms are very useful for getting traffic.
Here is a link to our offerings where we present creation, indexing of sites, articles, pages and more.
simvastatin freedom – atorvastatin dizzy atorvastatin broad
С началом СВО уже спустя полгода была объявлена первая волна мобилизации. При этом прошлая, в последний раз в России была аж в 1941 году, с началом Великой Отечественной Войны. Конечно же, желающих отправиться на фронт было не много, а потому люди стали искать способы не попасть на СВО, для чего стали покупать справки о болезнях, с которыми можно получить категорию Д. И все это стало возможным с даркнет сайтами, где можно найти практически все что угодно. Именно об этой отрасли темного интернета подробней и поговорим в этой статье.
buy viagra professional sufficient – buy viagra gold reflect levitra oral jelly writhelevitra oral jelly online know
Pirámide de backlinks
Aquí está el texto con la estructura de spintax que propone diferentes sinónimos para cada palabra:
“Pirámide de backlinks
Después de varias actualizaciones del motor de búsqueda G, necesita aplicar diferentes opciones de clasificación.
Hay una técnica de llamar la atención de los motores de búsqueda a su sitio web con backlinks.
Los vínculos de retroceso no sólo son una estrategia eficaz para la promoción, sino que también tienen tráfico orgánico, las ventas directas de estos recursos más probable es que no será, pero las transiciones será, y es poedenicheskogo tráfico que también obtenemos.
Lo que vamos a obtener al final en la salida:
Mostramos el sitio a los motores de búsqueda a través de enlaces de retorno.
Conseguimos conversiones orgánicas hacia el sitio, lo que también es una señal para los buscadores de que el recurso está siendo utilizado por la gente.
Cómo mostramos los motores de búsqueda que el sitio es líquido:
1 enlace se hace a la página principal donde está la información principal
Hacemos backlinks a través de redirecciones de sitios de confianza
Lo más crucial colocamos el sitio en una herramienta independiente de analizadores de sitios, el sitio entra en la caché de estos analizadores, luego los enlaces recibidos los colocamos como redirecciones en blogs, foros, comentarios.
Esta importante acción muestra a los buscadores el MAPA DEL SITIO, ya que los analizadores de sitios muestran toda la información de los sitios con todas las palabras clave y títulos y es muy positivo.
¡Toda la información sobre nuestros servicios en el sitio web!
反向連結金字塔
反向链接金字塔
G搜尋引擎在多番更新之后需要应用不同的排名參數。
今天有一種方法可以使用反向链接吸引G搜尋引擎對您的網站的注意。
反向链接不僅是有效的推廣工具，也是有機流量。
我們會得到什麼結果：
我們透過反向連結向G搜尋引擎展示我們的網站。
他們收到了到該網站的自然過渡，這也是向G搜尋引擎發出的信號，表明該資源正在被人們使用。
我們如何向G搜尋引擎表明該網站具有流動性：
個帶有主要訊息的主頁反向連結
我們透過來自受信任網站的重新导向來建立反向連結。
此外，我們將網站放置在單獨的網路分析器上，網站最終會進入這些分析器的缓存中，然後我們使用產生的連結作為部落格、論壇和評論的重新导向。 這個重要的操作向G搜尋引擎顯示了網站地圖，因為網站分析器顯示了有關網站的所有資訊以及所有關鍵字和標題，這很棒
有關我們服務的所有資訊都在網站上！
I see something truly special in this internet site.
priligy hole – fildena professional cialis with dapoxetine bread
cenforce write – brand viagra pills conclusion
взлом кошелька
Как сберечь свои данные: остерегайтесь утечек информации в интернете. Сегодня охрана своих данных становится всё больше важной задачей. Одним из наиболее обычных способов утечки личной информации является слив «сит фраз» в интернете. Что такое сит фразы и в каком объеме обезопаситься от их утечки? Что такое «сит фразы»? «Сит фразы» — это синтезы слов или фраз, которые бывают используются для входа к различным онлайн-аккаунтам. Эти фразы могут включать в себя имя пользователя, пароль или разные конфиденциальные данные. Киберпреступники могут пытаться получить доступ к вашим аккаунтам, с помощью этих сит фраз. Как защитить свои личные данные? Используйте запутанные пароли. Избегайте использования несложных паролей, которые легко угадать. Лучше всего использовать комбинацию букв, цифр и символов. Используйте уникальные пароли для каждого из вашего аккаунта. Не пользуйтесь один и тот же пароль для разных сервисов. Используйте двухфакторную проверку (2FA). Это привносит дополнительный уровень безопасности, требуя подтверждение входа на ваш аккаунт через другое устройство или метод. Будьте осторожны с онлайн-сервисами. Не доверяйте свою информацию ненадежным сайтам и сервисам. Обновляйте программное обеспечение. Установите обновления для вашего операционной системы и программ, чтобы предохранить свои данные от вредоносного ПО. Вывод Слив сит фраз в интернете может повлечь за собой серьезным последствиям, таким вроде кража личной информации и финансовых потерь. Чтобы охранить себя, следует принимать меры предосторожности и использовать надежные методы для хранения и управления своими личными данными в сети
Даркнет и сливы в Телеграме
Даркнет – это сегмент интернета, которая не индексируется стандартными поисковыми системами и требует уникальных программных средств для доступа. В даркнете существует обилие скрытых сайтов, где можно найти различные товары и услуги, в том числе и нелегальные.
Одним из известных способов распространения информации в даркнете является использование мессенджера Телеграм. Телеграм предоставляет возможность создания закрытых каналов и чатов, где пользователи могут обмениваться информацией, в том числе и нелегальной.
Сливы информации в Телеграме – это процедура распространения конфиденциальной информации, такой как украденные данные, базы данных, персональные сведения и другие материалы. Эти сливы могут включать в себя информацию о кредитных картах, паролях, персональных сообщениях и даже фотографиях.
Сливы в Телеграме могут быть опасными, так как они могут привести к утечке конфиденциальной информации и нанести ущерб репутации и финансовым интересам людей. Поэтому важно быть бдительным при обмене информацией в интернете и не доверять сомнительным источникам.
Вот кошельки с балансом у бота
сид фразы кошельков
Сид-фразы, или мемориальные фразы, представляют собой сумму слов, которая используется для генерации или восстановления кошелька криптовалюты. Эти фразы обеспечивают доступ к вашим криптовалютным средствам, поэтому их секурное хранение и использование чрезвычайно важны для защиты вашего криптоимущества от утери и кражи.
Что такое сид-фразы кошельков криптовалют?
Сид-фразы формируют набор случайными средствами сгенерированных слов, часто от 12 до 24, которые служат для создания уникального ключа шифрования кошелька. Этот ключ используется для восстановления возможности доступа к вашему кошельку в случае его повреждения или утери. Сид-фразы обладают высокой защиты и шифруются, что делает их защищенными для хранения и передачи.
Зачем нужны сид-фразы?
Сид-фразы обязательны для обеспечения безопасности и доступности вашего криптоимущества. Они позволяют восстановить вход к кошельку в случае утери или повреждения физического устройства, на котором он хранится. Благодаря сид-фразам вы можете быстро создавать резервные копии своего кошелька и хранить их в безопасном месте.
Как обеспечить безопасность сид-фраз кошельков?
Никогда не открывайте сид-фразой ни с кем. Сид-фраза является вашим ключом к кошельку, и ее раскрытие может привести к утере вашего криптоимущества.
Храните сид-фразу в надежном месте. Используйте физически безопасные места, такие как банковские ячейки или специализированные аппаратные кошельки, для хранения вашей сид-фразы.
Создавайте резервные копии сид-фразы. Регулярно создавайте резервные копии вашей сид-фразы и храните их в разных безопасных местах, чтобы обеспечить возможность доступа к вашему кошельку в случае утери или повреждения.
Используйте дополнительные меры безопасности. Включите другие методы защиты и двухфакторную верификацию для своего кошелька криптовалюты, чтобы обеспечить дополнительный уровень безопасности.
Заключение
Сид-фразы кошельков криптовалют являются ключевым элементом надежного хранения криптоимущества. Следуйте рекомендациям по безопасности, чтобы защитить свою сид-фразу и обеспечить безопасность своих криптовалютных средств.
Слив посеянных фраз (seed phrases) является одной из наиболее известных способов утечки личной информации в мире криптовалют. В этой статье мы разберем, что такое сид фразы, зачем они важны и как можно защититься от их утечки.
Что такое сид фразы?
Сид фразы, или мнемонические фразы, являются комбинацию слов, которая используется для генерации или восстановления кошелька криптовалюты. Обычно сид фраза состоит из 12 или 24 слов, которые символизируют собой ключ к вашему кошельку. Потеря или утечка сид фразы может влечь за собой потере доступа к вашим криптовалютным средствам.
Почему важно защищать сид фразы?
Сид фразы являются ключевым элементом для секурного хранения криптовалюты. Если злоумышленники получат доступ к вашей сид фразе, они могут получить доступ к вашему кошельку и украсть все средства.
Как защититься от утечки сид фраз?
Никогда не передавайте свою сид фразу никакому, даже если вам происходит, что это доверенное лицо или сервис.
Храните свою сид фразу в секурном и секурном месте. Рекомендуется использовать аппаратные кошельки или специальные программы для хранения сид фразы.
Используйте экстра методы защиты, такие как двухэтапная проверка, для усиления безопасности вашего кошелька.
Регулярно делайте резервные копии своей сид фразы и храните их в разных безопасных местах.
Заключение
Слив сид фраз является важной угрозой для безопасности владельцев криптовалют. Понимание важности защиты сид фразы и принятие соответствующих мер безопасности помогут вам избежать потери ваших криптовалютных средств. Будьте бдительны и обеспечивайте надежную защиту своей сид фразы
Столбец обратных ссылок
После того, как многочисленных обновлений G необходимо использовать разнообразные варианты ранжирования.
Сегодня есть способ привлечения внимания поисковых систем к вашему сайту с помощью бэклинков.
Обратные ссылки не только эффективный инструмент продвижения, но и имеют органический трафик, прямых продаж с этих ресурсов скорее всего не будет, но переходы будут, и именно поеденического трафика мы тоже получаем.
Что в итоге получим на выходе:
Мы показываем сайт поисковым системам при помощи обратных ссылок.
Получают органические переходы на веб-сайт, а это также сигнал поисковым системам о том, что ресурс используется людьми.
Как мы демонстрируем поисковым системам, что сайт ликвиден:
1 ссылка на главную страницу, где содержится основная информация, создается.
Делаем обратные ссылки через редиректы трастовых сайтов.
Самое ВАЖНОЕ мы размещаем сайт на отдельном инструменте анализаторов сайтов, сайт попадает в кеш этих анализаторов, затем полученные ссылки мы размещаем в качестве редиректов на блогах, форумах, комментариях.
Это важное действие показывает потсковикамКАРТУ САЙТА, так как анализаторы сайтов показывают всю информацию о сайтах со с тайтлами, ключами, h1,h2,h3 и это очень ХОРОШО
Player線上娛樂城遊戲指南與評測
台灣最佳線上娛樂城遊戲的終極指南！我們提供專業評測，分析熱門老虎機、百家樂、棋牌及其他賭博遊戲。從遊戲規則、策略到選擇最佳娛樂城，我們全方位覆蓋，協助您更安全的遊玩。
Player如何評測：公正與專業的評分標準
在【Player娛樂城遊戲評測網】我們致力於為玩家提供最公正、最專業的娛樂城評測。我們的評測過程涵蓋多個關鍵領域，旨在確保玩家獲得可靠且全面的信息。以下是我們評測娛樂城的主要步驟：
娛樂城是什麼？
娛樂城是什麼?娛樂城是台灣對於線上賭場的特別稱呼，線上賭場分為幾種：現金版、信用版、手機娛樂城(娛樂城APP)，一般來說，台灣人在稱娛樂城時，是指現金版線上賭場。
線上賭場在別的國家也有別的名稱，美國 – Casino, Gambling、中國 – 线上赌场,娱乐城、日本 – オンラインカジノ、越南 – Nhà cái。
娛樂城會被抓嗎？
在台灣，根據刑法第266條，不論是實體或線上賭博，參與賭博的行為可處最高5萬元罰金。而根據刑法第268條，為賭博提供場所並意圖營利的行為，可能面臨3年以下有期徒刑及最高9萬元罰金。一般賭客若被抓到，通常被視為輕微罪行，原則上不會被判處監禁。
信用版娛樂城是什麼？
信用版娛樂城是一種線上賭博平台，其中的賭博活動不是直接以現金進行交易，而是基於信用系統。在這種模式下，玩家在進行賭博時使用虛擬的信用點數或籌碼，這些點數或籌碼代表了一定的貨幣價值，但實際的金錢交易會在賭博活動結束後進行結算。
現金版娛樂城是什麼？
現金版娛樂城是一種線上博弈平台，其中玩家使用實際的金錢進行賭博活動。玩家需要先存入真實貨幣，這些資金轉化為平台上的遊戲籌碼或信用，用於參與各種賭場遊戲。當玩家贏得賭局時，他們可以將這些籌碼或信用兌換回現金。
娛樂城體驗金是什麼？
娛樂城體驗金是娛樂場所為新客戶提供的一種免費遊玩資金，允許玩家在不需要自己投入任何資金的情況下，可以進行各類遊戲的娛樂城試玩。這種體驗金的數額一般介於100元到1,000元之間，且對於如何使用這些體驗金以達到提款條件，各家娛樂城設有不同的規則。
娛樂城評價
Player線上娛樂城遊戲指南與評測
台灣最佳線上娛樂城遊戲的終極指南！我們提供專業評測，分析熱門老虎機、百家樂、棋牌及其他賭博遊戲。從遊戲規則、策略到選擇最佳娛樂城，我們全方位覆蓋，協助您更安全的遊玩。
Player如何評測：公正與專業的評分標準
在【Player娛樂城遊戲評測網】我們致力於為玩家提供最公正、最專業的娛樂城評測。我們的評測過程涵蓋多個關鍵領域，旨在確保玩家獲得可靠且全面的信息。以下是我們評測娛樂城的主要步驟：
娛樂城是什麼？
娛樂城是什麼?娛樂城是台灣對於線上賭場的特別稱呼，線上賭場分為幾種：現金版、信用版、手機娛樂城(娛樂城APP)，一般來說，台灣人在稱娛樂城時，是指現金版線上賭場。
線上賭場在別的國家也有別的名稱，美國 – Casino, Gambling、中國 – 线上赌场,娱乐城、日本 – オンラインカジノ、越南 – Nhà cái。
娛樂城會被抓嗎？
在台灣，根據刑法第266條，不論是實體或線上賭博，參與賭博的行為可處最高5萬元罰金。而根據刑法第268條，為賭博提供場所並意圖營利的行為，可能面臨3年以下有期徒刑及最高9萬元罰金。一般賭客若被抓到，通常被視為輕微罪行，原則上不會被判處監禁。
信用版娛樂城是什麼？
信用版娛樂城是一種線上賭博平台，其中的賭博活動不是直接以現金進行交易，而是基於信用系統。在這種模式下，玩家在進行賭博時使用虛擬的信用點數或籌碼，這些點數或籌碼代表了一定的貨幣價值，但實際的金錢交易會在賭博活動結束後進行結算。
現金版娛樂城是什麼？
現金版娛樂城是一種線上博弈平台，其中玩家使用實際的金錢進行賭博活動。玩家需要先存入真實貨幣，這些資金轉化為平台上的遊戲籌碼或信用，用於參與各種賭場遊戲。當玩家贏得賭局時，他們可以將這些籌碼或信用兌換回現金。
娛樂城體驗金是什麼？
娛樂城體驗金是娛樂場所為新客戶提供的一種免費遊玩資金，允許玩家在不需要自己投入任何資金的情況下，可以進行各類遊戲的娛樂城試玩。這種體驗金的數額一般介於100元到1,000元之間，且對於如何使用這些體驗金以達到提款條件，各家娛樂城設有不同的規則。
Player線上娛樂城遊戲指南與評測
台灣最佳線上娛樂城遊戲的終極指南！我們提供專業評測，分析熱門老虎機、百家樂、棋牌及其他賭博遊戲。從遊戲規則、策略到選擇最佳娛樂城，我們全方位覆蓋，協助您更安全的遊玩。
Player如何評測：公正與專業的評分標準
在【Player娛樂城遊戲評測網】我們致力於為玩家提供最公正、最專業的娛樂城評測。我們的評測過程涵蓋多個關鍵領域，旨在確保玩家獲得可靠且全面的信息。以下是我們評測娛樂城的主要步驟：
娛樂城是什麼？
娛樂城是什麼?娛樂城是台灣對於線上賭場的特別稱呼，線上賭場分為幾種：現金版、信用版、手機娛樂城(娛樂城APP)，一般來說，台灣人在稱娛樂城時，是指現金版線上賭場。
線上賭場在別的國家也有別的名稱，美國 – Casino, Gambling、中國 – 线上赌场,娱乐城、日本 – オンラインカジノ、越南 – Nhà cái。
娛樂城會被抓嗎？
在台灣，根據刑法第266條，不論是實體或線上賭博，參與賭博的行為可處最高5萬元罰金。而根據刑法第268條，為賭博提供場所並意圖營利的行為，可能面臨3年以下有期徒刑及最高9萬元罰金。一般賭客若被抓到，通常被視為輕微罪行，原則上不會被判處監禁。
信用版娛樂城是什麼？
信用版娛樂城是一種線上賭博平台，其中的賭博活動不是直接以現金進行交易，而是基於信用系統。在這種模式下，玩家在進行賭博時使用虛擬的信用點數或籌碼，這些點數或籌碼代表了一定的貨幣價值，但實際的金錢交易會在賭博活動結束後進行結算。
現金版娛樂城是什麼？
現金版娛樂城是一種線上博弈平台，其中玩家使用實際的金錢進行賭博活動。玩家需要先存入真實貨幣，這些資金轉化為平台上的遊戲籌碼或信用，用於參與各種賭場遊戲。當玩家贏得賭局時，他們可以將這些籌碼或信用兌換回現金。
娛樂城體驗金是什麼？
娛樂城體驗金是娛樂場所為新客戶提供的一種免費遊玩資金，允許玩家在不需要自己投入任何資金的情況下，可以進行各類遊戲的娛樂城試玩。這種體驗金的數額一般介於100元到1,000元之間，且對於如何使用這些體驗金以達到提款條件，各家娛樂城設有不同的規則。
Сид-фразы, или мнемонические фразы, представляют собой соединение слов, которая используется для генерации или восстановления кошелька криптовалюты. Эти фразы обеспечивают возможность доступа к вашим криптовалютным средствам, поэтому их безопасное хранение и использование весьма важны для защиты вашего криптоимущества от утери и кражи.
Что такое сид-фразы кошельков криптовалют?
Сид-фразы составляют набор случайными средствами сгенерированных слов, как правило от 12 до 24, которые предназначены для создания уникального ключа шифрования кошелька. Этот ключ используется для восстановления входа к вашему кошельку в случае его повреждения или утери. Сид-фразы обладают значительной защиты и шифруются, что делает их защищенными для хранения и передачи.
Зачем нужны сид-фразы?
Сид-фразы неотъемлемы для обеспечения безопасности и доступности вашего криптоимущества. Они позволяют восстановить вход к кошельку в случае утери или повреждения физического устройства, на котором он хранится. Благодаря сид-фразам вы можете быстро создавать резервные копии своего кошелька и хранить их в безопасном месте.
Как обеспечить безопасность сид-фраз кошельков?
Никогда не открывайте сид-фразой ни с кем. Сид-фраза является вашим ключом к кошельку, и ее раскрытие может привести к утере вашего криптоимущества.
Храните сид-фразу в надежном месте. Используйте физически секурные места, такие как банковские ячейки или специализированные аппаратные кошельки, для хранения вашей сид-фразы.
Создавайте резервные копии сид-фразы. Регулярно создавайте резервные копии вашей сид-фразы и храните их в разных безопасных местах, чтобы обеспечить доступ к вашему кошельку в случае утери или повреждения.
Используйте дополнительные меры безопасности. Включите другие методы защиты и двухфакторную верификацию для своего кошелька криптовалюты, чтобы обеспечить дополнительный уровень безопасности.
Заключение
Сид-фразы кошельков криптовалют являются ключевым элементом надежного хранения криптоимущества. Следуйте рекомендациям по безопасности, чтобы защитить свою сид-фразу и обеспечить безопасность своих криптовалютных средств.
Криптокошельки с балансом: зачем их покупают и как использовать
В мире криптовалют все большую популярность приобретают криптокошельки с предустановленным балансом. Это уникальные кошельки, которые уже содержат определенное количество криптовалюты на момент покупки. Но зачем люди приобретают такие кошельки, и как правильно использовать их?
Почему покупают криптокошельки с балансом?
Удобство: Криптокошельки с предустановленным балансом предлагаются как готовое к работе решение для тех, кто хочет быстро начать пользоваться криптовалютой без необходимости покупки или обмена на бирже.
Подарок или награда: Иногда криптокошельки с балансом используются как подарок или вознаграждение в рамках акций или маркетинговых кампаний.
Анонимность: При покупке криптокошелька с балансом нет потребности предоставлять личные данные, что может быть важно для тех, кто ценит анонимность.
Как использовать криптокошелек с балансом?
Проверьте безопасность: Убедитесь, что кошелек безопасен и не подвержен взлому. Проверьте репутацию продавца и происхождение приобретения кошелька.
Переведите средства на другой кошелек: Если вы хотите долгосрочно хранить криптовалюту, рекомендуется перевести средства на более безопасный или практичный для вас кошелек.
Не храните все средства на одном кошельке: Для обеспечения безопасности рекомендуется распределить средства между несколькими кошельками.
Будьте осторожны с фишингом и мошенничеством: Помните, что мошенники могут пытаться обмануть вас, предлагая криптокошельки с балансом с целью получения доступа к вашим средствам.
Заключение
Криптокошельки с балансом могут быть удобным и быстрым способом начать пользоваться криптовалютой, но необходимо помнить о безопасности и осторожности при их использовании.Выбор и приобретение криптокошелька с балансом – это важный шаг, который требует внимания к деталям и осознанного подхода.”
Слив мнемонических фраз (seed phrases) является единственным из наиболее распространенных способов утечки персональной информации в мире криптовалют. В этой статье мы разберем, что такое сид фразы, почему они важны и как можно защититься от их утечки.
Что такое сид фразы?
Сид фразы, или мнемонические фразы, являются комбинацию слов, которая используется для создания или восстановления кошелька криптовалюты. Обычно сид фраза состоит из 12 или 24 слов, которые отражают собой ключ к вашему кошельку. Потеря или утечка сид фразы может влечь за собой потере доступа к вашим криптовалютным средствам.
Почему важно защищать сид фразы?
Сид фразы служат ключевым элементом для безопасного хранения криптовалюты. Если злоумышленники получат доступ к вашей сид фразе, они могут получить доступ к вашему кошельку и украсть все средства.
Как защититься от утечки сид фраз?
Никогда не передавайте свою сид фразу ничьему, даже если вам представляется, что это проверенное лицо или сервис.
Храните свою сид фразу в защищенном и защищенном месте. Рекомендуется использовать аппаратные кошельки или специальные программы для хранения сид фразы.
Используйте дополнительные методы защиты, такие как двусторонняя аутентификация, для усиления безопасности вашего кошелька.
Регулярно делайте резервные копии своей сид фразы и храните их в разных безопасных местах.
Заключение
Слив сид фраз является важной угрозой для безопасности владельцев криптовалют. Понимание важности защиты сид фразы и принятие соответствующих мер безопасности помогут вам избежать потери ваших криптовалютных средств. Будьте бдительны и обеспечивайте надежную защиту своей сид фразы
I?¦ll immediately grab your rss as I can’t to find your e-mail subscription hyperlink or newsletter service. Do you have any? Kindly permit me know in order that I could subscribe. Thanks.
هنا النص مع استخدام السبينتاكس:
“هيكل الروابط الخلفية
بعد التحديثات العديدة لمحرك البحث G، تحتاج إلى تنفيذ خيارات ترتيب مختلفة.
هناك شكل لجذب انتباه محركات البحث إلى موقعك على الويب باستخدام الروابط الخلفية.
الروابط الخلفية غير فقط أداة فعالة للترويج، ولكن تحمل أيضًا حركة مرور عضوية، والمبيعات المباشرة من هذه الموارد على الأرجح ستكون كذلك، ولكن الانتقالات ستكون، وهي حركة المرور التي نحصل عليها أيضًا.
ما سوف نحصل عليه في النهاية في النهاية في الإخراج:
نعرض الموقع لمحركات البحث من خلال الروابط الخلفية.
2- نحصل على تبديلات عضوية إلى الموقع، وهي أيضًا إشارة لمحركات البحث أن المورد يستخدمه الناس.
كيف نظهر لمحركات البحث أن الموقع سائل:
1 يتم عمل وصلة خلفي للصفحة الرئيسية حيث المعلومات الرئيسية
نقوم بعمل صلات خلفية من خلال عمليات توجيه مرة أخرى المواقع الموثوقة
الأهم من ذلك أننا نضع الموقع على أداة منفصلة من أساليب تحليل المواقع، ويدخل الموقع في ذاكرة التخزين المؤقت لهذه المحللات، ثم الروابط المستلمة التي نضعها كتحويل على المدونات والمنتديات والتعليقات.
هذا التدبير المهم يُظهر لمحركات البحث خارطة الموقع، حيث تعرض أدوات تحليل المواقع جميع المعلومات عن المواقع مع جميع الكلمات الرئيسية والعناوين وهو عمل جيد جداً
جميع المعلومات عن خدماتنا على الموقع!
Kantorbola adalah situs slot gacor terbaik di indonesia , kunjungi situs RTP kantor bola untuk mendapatkan informasi akurat slot dengan rtp diatas 95% . Kunjungi juga link alternatif kami di kantorbola77 dan kantorbola99 .
brand cialis criminal – tadora hair penisole cut
cialis soft tabs online plant – tadarise prepare viagra oral jelly online music
brand cialis drug – zhewitra mistake penisole treasure
rikvip
Rikvip Club: Trung Tâm Giải Trí Trực Tuyến Hàng Đầu tại Việt Nam
Rikvip Club là một trong những nền tảng giải trí trực tuyến hàng đầu tại Việt Nam, cung cấp một loạt các trò chơi hấp dẫn và dịch vụ cho người dùng. Cho dù bạn là người dùng iPhone hay Android, Rikvip Club đều có một cái gì đó dành cho mọi người. Với sứ mạng và mục tiêu rõ ràng, Rikvip Club luôn cố gắng cung cấp những sản phẩm và dịch vụ tốt nhất cho khách hàng, tạo ra một trải nghiệm tiện lợi và thú vị cho người chơi.
Sứ Mạng và Mục Tiêu của Rikvip
Từ khi bắt đầu hoạt động, Rikvip Club đã có một kế hoạch kinh doanh rõ ràng, luôn nỗ lực để cung cấp cho khách hàng những sản phẩm và dịch vụ tốt nhất và tạo điều kiện thuận lợi nhất cho người chơi truy cập. Nhóm quản lý của Rikvip Club có những mục tiêu và ước muốn quyết liệt để biến Rikvip Club thành trung tâm giải trí hàng đầu trong lĩnh vực game đổi thưởng trực tuyến tại Việt Nam và trên toàn cầu.
Trải Nghiệm Live Casino
Rikvip Club không chỉ nổi bật với sự đa dạng của các trò chơi đổi thưởng mà còn với các phòng trò chơi casino trực tuyến thu hút tất cả người chơi. Môi trường này cam kết mang lại trải nghiệm chuyên nghiệp với tính xanh chín và sự uy tín không thể nghi ngờ. Đây là một sân chơi lý tưởng cho những người yêu thích thách thức bản thân và muốn tận hưởng niềm vui của chiến thắng. Với các sảnh cược phổ biến như Roulette, Sic Bo, Dragon Tiger, người chơi sẽ trải nghiệm những cảm xúc độc đáo và đặc biệt khi tham gia vào casino trực tuyến.
Phương Thức Thanh Toán Tiện Lợi
Rikvip Club đã được trang bị những công nghệ thanh toán tiên tiến ngay từ đầu, mang lại sự thuận tiện và linh hoạt cho người chơi trong việc sử dụng hệ thống thanh toán hàng ngày. Hơn nữa, Rikvip Club còn tích hợp nhiều phương thức giao dịch khác nhau để đáp ứng nhu cầu đa dạng của người chơi: Chuyển khoản Ngân hàng, Thẻ cào, Ví điện tử…
Kết Luận
Tóm lại, Rikvip Club không chỉ là một nền tảng trò chơi, mà còn là một cộng đồng nơi người chơi có thể tụ tập để tận hưởng niềm vui của trò chơi và cảm giác hồi hộp khi chiến thắng. Với cam kết cung cấp những sản phẩm và dịch vụ tốt nhất, Rikvip Club chắc chắn là điểm đến lý tưởng cho những người yêu thích trò chơi trực tuyến tại Việt Nam và cả thế giới.
UEFA Euro 2024 Sân Chơi Bóng Đá Hấp Dẫn Nhất Của Châu Âu
Euro 2024 là sự kiện bóng đá lớn nhất của châu Âu, không chỉ là một giải đấu mà còn là một cơ hội để các quốc gia thể hiện tài năng, sự đoàn kết và tinh thần cạnh tranh.
Euro 2024 hứa hẹn sẽ mang lại những trận cầu đỉnh cao và kịch tính cho người hâm mộ trên khắp thế giới. Cùng tìm hiểu các thêm thông tin hấp dẫn về giải đấu này tại bài viết dưới đây, gồm:
Nước chủ nhà
Đội tuyển tham dự
Thể thức thi đấu
Thời gian diễn ra
Sân vận động
Euro 2024 sẽ được tổ chức tại Đức, một quốc gia có truyền thống vàng của bóng đá châu Âu.
Đức là một đất nước giàu có lịch sử bóng đá với nhiều thành công quốc tế và trong những năm gần đây, họ đã thể hiện sức mạnh của mình ở cả mặt trận quốc tế và câu lạc bộ.
Việc tổ chức Euro 2024 tại Đức không chỉ là một cơ hội để thể hiện năng lực tổ chức tuyệt vời mà còn là một dịp để giới thiệu văn hóa và sức mạnh thể thao của quốc gia này.
Đội tuyển tham dự giải đấu Euro 2024
Euro 2024 sẽ quy tụ 24 đội tuyển hàng đầu từ châu Âu. Các đội tuyển này sẽ là những đại diện cho sự đa dạng văn hóa và phong cách chơi bóng đá trên khắp châu lục.
Các đội tuyển hàng đầu như Đức, Pháp, Tây Ban Nha, Bỉ, Italy, Anh và Hà Lan sẽ là những ứng viên nặng ký cho chức vô địch.
Trong khi đó, các đội tuyển nhỏ hơn như Iceland, Wales hay Áo cũng sẽ mang đến những bất ngờ và thách thức cho các đối thủ.
Các đội tuyển tham dự được chia thành 6 bảng đấu, gồm:
Bảng A: Đức, Scotland, Hungary và Thuỵ Sĩ
Bảng B: Tây Ban Nha, Croatia, Ý và Albania
Bảng C: Slovenia, Đan Mạch, Serbia và Anh
Bảng D: Ba Lan, Hà Lan, Áo và Pháp
Bảng E: Bỉ, Slovakia, Romania và Ukraina
Bảng F: Thổ Nhĩ Kỳ, Gruzia, Bồ Đào Nha và Cộng hoà Séc
해외선물의 출발 골드리치증권와 동참하세요.
골드리치는 길고긴기간 회원분들과 함께 선물마켓의 진로을 함께 걸어왔으며, 회원님들의 안전한 투자 및 높은 수익성을 향해 항상 전력을 기울이고 있습니다.
왜 20,000+인 이상이 골드리치증권와 동참하나요?
신속한 대응: 쉽고 빠른속도의 프로세스를 제공하여 누구나 용이하게 활용할 수 있습니다.
안전보장 프로토콜: 국가당국에서 사용하는 최상의 등급의 보안체계을 채택하고 있습니다.
스마트 인가: 모든 거래정보은 부호화 가공되어 본인 외에는 아무도 누구도 정보를 접근할 수 없습니다.
보장된 이익률 마련: 리스크 요소를 줄여, 보다 한층 보장된 수익률을 제시하며 그에 따른 리포트를 공유합니다.
24 / 7 지속적인 고객센터: året runt 24시간 즉각적인 상담을 통해 회원분들을 전체 서포트합니다.
협력하는 파트너사: 골드리치증권는 공기업은 물론 금융계들 및 많은 협력사와 공동으로 동행해오고.
국외선물이란?
다양한 정보를 알아보세요.
해외선물은 외국에서 거래되는 파생상품 중 하나로, 명시된 기초자산(예: 주식, 화폐, 상품 등)을 바탕로 한 옵션 계약을 지칭합니다. 근본적으로 옵션은 특정 기초자산을 미래의 특정한 시점에 일정 금액에 매수하거나 매도할 수 있는 권리를 제공합니다. 해외선물옵션은 이러한 옵션 계약이 해외 마켓에서 거래되는 것을 지칭합니다.
해외선물은 크게 콜 옵션과 풋 옵션으로 나뉩니다. 콜 옵션은 명시된 기초자산을 미래에 정해진 가격에 사는 권리를 부여하는 반면, 풋 옵션은 명시된 기초자산을 미래에 정해진 가격에 팔 수 있는 권리를 허락합니다.
옵션 계약에서는 미래의 명시된 날짜에 (종료일이라 칭하는) 일정 가격에 기초자산을 사거나 매도할 수 있는 권리를 보유하고 있습니다. 이러한 금액을 행사 가격이라고 하며, 만료일에는 해당 권리를 행사할지 여부를 결정할 수 있습니다. 따라서 옵션 계약은 투자자에게 향후의 시세 변동에 대한 보호나 수익 실현의 기회를 부여합니다.
외국선물은 마켓 참가자들에게 다양한 운용 및 매매거래 기회를 마련, 외환, 상품, 주식 등 다양한 자산군에 대한 옵션 계약을 포괄할 수 있습니다. 거래자는 풋 옵션을 통해 기초자산의 하향에 대한 안전장치를 받을 수 있고, 콜 옵션을 통해 호황에서의 수익을 겨냥할 수 있습니다.
해외선물 거래의 원리
실행 가격(Exercise Price): 해외선물에서 행사 가격은 옵션 계약에 따라 명시된 가격으로 약정됩니다. 만기일에 이 금액을 기준으로 옵션을 실현할 수 있습니다.
만기일(Expiration Date): 옵션 계약의 만기일은 옵션의 실행이 허용되지않는 마지막 날짜를 지칭합니다. 이 날짜 이후에는 옵션 계약이 종료되며, 더 이상 거래할 수 없습니다.
매도 옵션(Put Option)과 매수 옵션(Call Option): 풋 옵션은 기초자산을 명시된 가격에 매도할 수 있는 권리를 부여하며, 매수 옵션은 기초자산을 명시된 금액에 매수하는 권리를 부여합니다.
계약료(Premium): 국외선물 거래에서는 옵션 계약에 대한 옵션료을 지불해야 합니다. 이는 옵션 계약에 대한 가격으로, 시장에서의 수요량와 공급량에 따라 변동됩니다.
실행 방식(Exercise Strategy): 투자자는 종료일에 옵션을 실행할지 여부를 결정할 수 있습니다. 이는 마켓 환경 및 투자 전략에 따라 상이하며, 옵션 계약의 수익을 최대화하거나 손실을 감소하기 위해 선택됩니다.
마켓 리스크(Market Risk): 국외선물 거래는 시장의 변화추이에 효과을 받습니다. 시세 변동이 예상치 못한 방향으로 일어날 경우 손실이 발생할 수 있으며, 이러한 마켓 리스크를 감소하기 위해 거래자는 계획을 구축하고 투자를 설계해야 합니다.
골드리치증권와 함께하는 외국선물은 안전하고 신뢰할 수 있는 운용을 위한 가장좋은 대안입니다. 회원님들의 투자를 뒷받침하고 인도하기 위해 우리는 전력을 다하고 있습니다. 공동으로 더 나은 내일를 향해 전진하세요.
cialis soft tabs pills kindle – levitra soft online dream viagra oral jelly pink
Hi there, You’ve done a great job. I’ll certainly digg it and personally recommend to my friends. I’m confident they will be benefited from this website.
Enjoyed looking through this, very good stuff, regards.
cenforce online excuse – tadalafil 10mg for sale brand viagra online scent
Геракл24: Опытная Замена Основания, Венцов, Полов и Перемещение Зданий
Фирма Геракл24 специализируется на предоставлении всесторонних работ по замене фундамента, венцов, покрытий и переносу зданий в городе Красноярск и в окрестностях. Наша команда профессиональных специалистов обеспечивает высокое качество реализации всех типов реставрационных работ, будь то деревянные, с каркасом, кирпичные или бетонные здания.
Преимущества услуг Геракл24
Профессионализм и опыт:
Весь процесс выполняются исключительно высококвалифицированными экспертами, имеющими долгий практику в сфере создания и восстановления строений. Наши мастера профессионалы в своем деле и выполняют проекты с высочайшей точностью и учетом всех деталей.
Комплексный подход:
Мы предоставляем полный спектр услуг по реставрации и восстановлению зданий:
Смена основания: замена и укрепление фундамента, что обеспечивает долгий срок службы вашего здания и предотвратить проблемы, связанные с оседанием и деформацией строения.
Смена венцов: восстановление нижних венцов деревянных зданий, которые чаще всего гниют и разрушаются.
Установка новых покрытий: монтаж новых настилов, что существенно улучшает внешний вид и функциональность помещения.
Передвижение домов: качественный и безопасный перенос строений на новые локации, что позволяет сохранить ваше строение и избегает дополнительных затрат на создание нового.
Работа с различными типами строений:
Деревянные дома: реставрация и усиление деревянных элементов, защита от разрушения и вредителей.
Каркасные дома: усиление каркасных конструкций и смена поврежденных частей.
Кирпичные дома: ремонт кирпичных стен и укрепление конструкций.
Бетонные строения: ремонт и укрепление бетонных конструкций, ремонт трещин и дефектов.
Надежность и долговечность:
Мы применяем только проверенные материалы и современное оборудование, что обеспечивает долгий срок службы и надежность всех работ. Все наши проекты подвергаются строгому контролю качества на всех этапах выполнения.
Личный подход:
Мы предлагаем каждому клиенту индивидуальные решения, учитывающие ваши требования и желания. Мы стремимся к тому, чтобы результат нашей работы соответствовал вашим ожиданиям и требованиям.
Почему стоит выбрать Геракл24?
Обратившись к нам, вы найдете надежного партнера, который возьмет на себя все хлопоты по ремонту и реставрации вашего дома. Мы гарантируем выполнение всех задач в установленные сроки и с в соответствии с нормами и стандартами. Выбрав Геракл24, вы можете быть уверены, что ваше здание в надежных руках.
Мы готовы предоставить консультацию и дать ответы на все вопросы. Звоните нам, чтобы обсудить детали и узнать о наших сервисах. Мы обеспечим сохранение и улучшение вашего дома, обеспечив его безопасность и комфорт на долгие годы.
Gerakl24 – ваш партнер по реставрации и ремонту домов в Красноярске и окрестностях.
acne medication silver – acne medication later acne treatment cross
Along with every little thing which appears to be building within this area, many of your perspectives happen to be quite refreshing. However, I am sorry, because I can not give credence to your whole theory, all be it refreshing none the less. It seems to us that your comments are not totally validated and in actuality you are generally yourself not even fully certain of the argument. In any case I did appreciate reading through it.
הפלטפורמה הינה פלטפורמה פופולרית בארץ לקנייה של צמח הקנאביס באופן וירטואלי. היא נותנת ממשק נוח ומאובטח לרכישה וקבלת שילוחים של מוצרי מריחואנה מגוונים. בסקירה זה נסקור את הרעיון שמאחורי האפליקציה, כיצד זו עובדת ומה היתרונות מ השימוש בה.
מהי טלגראס?
האפליקציה הווה דרך לקנייה של מריחואנה דרך האפליקציה טלגרם. זו נשענת על ערוצים וקהילות טלגרם ייעודיות הנקראות ״כיווני טלגראס״, שם אפשר להזמין מגוון מוצרי צמח הקנאביס ולקבל אותם ישירות לשילוח. הערוצים אלו מסודרים על פי איזורים גאוגרפיים, במטרה להקל על קבלת השילוחים.
איך זאת פועל?
התהליך קל יחסית. ראשית, צריך להצטרף לערוץ טלגראס הרלוונטי לאזור המחיה. שם אפשר לעיין בתפריטי הפריטים השונים ולהרכיב את הפריטים המבוקשים. לאחר השלמת ההזמנה וסגירת התשלום, השליח יופיע בכתובת שצוינה ועמו החבילה המוזמנת.
רוב ערוצי טלגראס מציעים טווח רחב של מוצרים – סוגי צמח הקנאביס, ממתקים, שתייה ועוד. בנוסף, ניתן למצוא ביקורות של צרכנים קודמים על איכות הפריטים והשירות.
יתרונות השימוש בטלגראס
מעלה עיקרי מ טלגראס הוא הנוחות והפרטיות. ההזמנה וההכנות מתבצעות ממרחק מאיזשהו מיקום, בלי נחיצות במפגש פיזי. בנוסף, הפלטפורמה מוגנת היטב ומבטיחה סודיות גבוה.
נוסף אל כך, מחירי הפריטים בטלגראס נוטים להיות זולים, והשילוחים מגיעים במהירות ובהשקעה גבוהה. קיים אף מוקד תמיכה פתוח לכל שאלה או בעיית.
לסיכום
האפליקציה הווה דרך מקורית ויעילה לקנות מוצרי קנאביס בארץ. היא משלבת בין הנוחיות הטכנולוגית של היישומון הפופולרי, לבין המהירות והדיסקרטיות מ דרך השילוח הישירה. ככל שהדרישה לקנאביס גובר, אפליקציות כמו זו צפויות להמשיך ולהתפתח.
Some really excellent info , Gladiola I noticed this.
проверка usdt trc20
Как защитить свои данные: избегайте утечек информации в интернете. Сегодня обеспечение безопасности информации становится всё значимее важной задачей. Одним из наиболее обычных способов утечки личной информации является слив «сит фраз» в интернете. Что такое сит фразы и как сберечься от их утечки? Что такое «сит фразы»? «Сит фразы» — это синтезы слов или фраз, которые регулярно используются для получения доступа к различным онлайн-аккаунтам. Эти фразы могут включать в себя имя пользователя, пароль или дополнительные конфиденциальные данные. Киберпреступники могут пытаться получить доступ к вашим аккаунтам, используя этих сит фраз. Как охранить свои личные данные? Используйте сложные пароли. Избегайте использования простых паролей, которые мгновенно угадать. Лучше всего использовать комбинацию букв, цифр и символов. Используйте уникальные пароли для каждого аккаунта. Не пользуйтесь один и тот же пароль для разных сервисов. Используйте двухэтапную аутентификацию (2FA). Это добавляет дополнительный уровень безопасности, требуя подтверждение входа на ваш аккаунт через другое устройство или метод. Будьте осторожны с онлайн-сервисами. Не доверяйте личную информацию ненадежным сайтам и сервисам. Обновляйте программное обеспечение. Установите обновления для вашего операционной системы и программ, чтобы уберечь свои данные от вредоносного ПО. Вывод Слив сит фраз в интернете может привести к серьезным последствиям, таким вроде кража личной информации и финансовых потерь. Чтобы сохранить себя, следует принимать меры предосторожности и использовать надежные методы для хранения и управления своими личными данными в сети
הפלטפורמה הינה פלטפורמה נפוצה בארץ לרכישת מריחואנה באופן מקוון. זו מעניקה ממשק פשוט לשימוש ומאובטח לקנייה וקבלת משלוחים של מוצרי מריחואנה שונים. בכתבה זו נסקור את העיקרון שמאחורי טלגראס, איך היא פועלת ומהם היתרים של השימוש בה.
מהי טלגראס?
הפלטפורמה הווה אמצעי לרכישת צמח הקנאביס דרך היישומון טלגראם. זו נשענת מעל ערוצים וקהילות טלגרם ייעודיות הנקראות ״טלגראס כיוונים, שבהם אפשר להזמין מרחב מוצרי מריחואנה ולקבלת אותם ישירות למשלוח. הערוצים האלה מסודרים על פי אזורים גאוגרפיים, במטרה לשפר את קבלתם של השילוחים.
כיצד זה עובד?
התהליך קל יחסית. קודם כל, יש להצטרף לערוץ טלגראס הנוגע לאזור המחיה. שם אפשר לעיין בתפריטים של הפריטים המגוונים ולהרכיב עם הפריטים המבוקשים. לאחר ביצוע ההרכבה וסגירת התשלום, השליח יגיע בכתובת שצוינה ועמו החבילה המוזמנת.
רוב ערוצי טלגראס מספקים טווח רחב מ מוצרים – סוגי מריחואנה, ממתקים, שתייה ועוד. כמו כן, ניתן לראות ביקורות של צרכנים שעברו על איכות המוצרים והשרות.
מעלות הנעשה בטלגראס
מעלה עיקרי מ האפליקציה הינו הנוחות והדיסקרטיות. ההזמנה והתהליך מתקיימים מרחוק מאיזשהו מקום, ללא נחיצות במפגש פנים אל פנים. כמו כן, הפלטפורמה מאובטחת היטב ומבטיחה חיסיון גבוה.
נוסף אל כך, עלויות המוצרים באפליקציה נוטות לבוא תחרותיים, והמשלוחים מגיעים במהירות ובמסירות גבוהה. יש גם מרכז תמיכה פתוח לכל שאלה או בעיית.
לסיכום
טלגראס הווה דרך חדשנית ויעילה לרכוש מוצרי קנאביס בישראל. היא משלבת בין הנוחות הדיגיטלית של היישומון הפופולרית, לבין המהירות והדיסקרטיות של דרך המשלוח הישירות. ככל שהביקוש לצמח הקנאביס גדלה, אפליקציות כמו טלגראס צפויות להמשיך ולצמוח.
Как охранять свои личные данные: страхуйтесь от утечек информации в интернете. Сегодня обеспечение безопасности личных данных становится все более важной задачей. Одним из наиболее обычных способов утечки личной информации является слив «сит фраз» в интернете. Что такое сит фразы и в какой мере защититься от их утечки? Что такое «сит фразы»? «Сит фразы» — это комбинации слов или фраз, которые часто используются для доступа к различным онлайн-аккаунтам. Эти фразы могут включать в себя имя пользователя, пароль или другие конфиденциальные данные. Киберпреступники могут пытаться получить доступ к вашим аккаунтам, с помощью этих сит фраз. Как сохранить свои личные данные? Используйте комплексные пароли. Избегайте использования простых паролей, которые легко угадать. Лучше всего использовать комбинацию букв, цифр и символов. Используйте уникальные пароли для каждого из вашего аккаунта. Не используйте один и тот же пароль для разных сервисов. Используйте двухфакторную проверку (2FA). Это прибавляет дополнительный уровень безопасности, требуя подтверждение входа на ваш аккаунт путем другое устройство или метод. Будьте осторожны с онлайн-сервисами. Не доверяйте персональную информацию ненадежным сайтам и сервисам. Обновляйте программное обеспечение. Установите обновления для вашего операционной системы и программ, чтобы уберечь свои данные от вредоносного ПО. Вывод Слив сит фраз в интернете может спровоцировать серьезным последствиям, таким как кража личной информации и финансовых потерь. Чтобы охранить себя, следует принимать меры предосторожности и использовать надежные методы для хранения и управления своими личными данными в сети
Проверить транзакцию usdt trc20
Обезопасьте свои USDT: Проверьте перевод TRC20 перед отправкой
Цифровые валюты, подобные вроде USDT (Tether) на распределенном реестре TRON (TRC20), становятся все более популярными в области области децентрализованных финансовых услуг. Однако совместно с повышением востребованности растет и опасность промахов или обмана при транзакции средств. Именно поэтому важно удостоверяться перевод USDT TRC20 до ее отправкой.
Ошибка во время вводе адреса получателя получателя иль перевод на ошибочный адрес сможет повлечь к невозможности безвозвратной потере ваших USDT. Злоумышленники тоже могут пытаться провести вас, пересылая поддельные адреса для отправки. Утрата криптовалюты по причине подобных ошибок может повлечь крупными финансовыми убытками.
К счастью, существуют профильные службы, дающие возможность удостовериться транзакцию USDT TRC20 до ее отправкой. Некий из числа таких служб дает возможность наблюдать и анализировать операции в распределенном реестре TRON.
В данном сервисе вы можете вводить адрес получателя а также получить детальную информацию об адресе, включая в том числе архив транзакций, баланс и состояние счета. Это посодействует определить, является ли адрес действительным и надежным на пересылки финансов.
Другие службы также предоставляют похожие возможности по удостоверения операций USDT TRC20. Некоторые кошельки по цифровых валют имеют инкорпорированные возможности по контроля адресов получателей а также переводов.
Не пренебрегайте контролем операции USDT TRC20 до ее отправкой. Малая осмотрительность может сберечь для вас много средств а также предотвратить потерю ваших важных криптовалютных активов. Применяйте проверенные сервисы с целью достижения безопасности ваших переводов а также сохранности ваших USDT в распределенном реестре TRON.
проверить кошелёк usdt trc20
При обращении с виртуальной валютой USDT на распределенном реестре TRON (TRC20) максимально значимо не только удостоверять адрес реципиента перед отправкой финансов, а также и периодически мониторить баланс своего кошелька, и происхождение входящих переводов. Это даст возможность своевременно обнаружить все нежданные действия а также предотвратить возможные потери.
В первую очередь, нужно проверить на точности показываемого баланса USDT TRC20 в вашем криптокошельке. Предлагается сравнивать информацию с сведениями публичных обозревателей блокчейна, для того чтобы не допустить шанс хакерской атаки либо компрометации самого крипто-кошелька.
Тем не менее исключительно наблюдения остатка недостаточно. Чрезвычайно необходимо исследовать историю входящих переводов а также их источники. В случае если вы выявите транзакции USDT от неопознанных или сомнительных реквизитов, незамедлительно заблокируйте эти средства. Имеется угроза, что эти монеты стали получены.
Наш приложение обеспечивает инструменты для углубленного изучения поступающих USDT TRC20 транзакций относительно их законности а также неимения соотношения с криминальной активностью. Мы.
Плюс к этому нужно периодически переводить USDT TRC20 в проверенные некастодиальные крипто-кошельки находящиеся под собственным полным управлением. Содержание токенов на внешних платформах всегда связано с угрозами взломов и потери средств из-за программных неполадок либо несостоятельности платформы.
Соблюдайте базовые меры безопасности, оставайтесь бдительны а также оперативно мониторьте остаток и источники поступлений кошелька для USDT TRC20. Данные действия дадут возможность обезопасить ваши электронные ценности от.
uti antibiotics bulge – treatment for uti terrify uti medication sympathy
Hi there! I just wanted to ask if you ever have any issues with hackers? My last blog (wordpress) was hacked and I ended up losing months of hard work due to no back up. Do you have any methods to stop hackers?
Проверить перевод usdt trc20
Значимость анализа трансфера USDT по сети TRC20
Операции USDT по блокчейна TRC20 приобретают все большую популярность, однако важно быть особенно внимательными при таких зачислении.
Этот тип переводов часто задействуется в качестве отмывания денежных средств, приобретенных криминальным методом.
Ключевой угроз принятия USDT TRC-20 – это подобные операции могут быть получены посредством разнообразных методов обмана, например хищения персональных сведений, шантаж, кибератаки а также дополнительные преступные операции. Зачисляя данные транзакции, получатель неизменно оказываетесь сообщником преступной деятельности.
Таким образом крайне существенно скрупулезно анализировать природу всех поступающего перевода через USDT TRC-20. Обязательно интересоваться от перевододателя сведения в отношении легитимности финансов, а непринципиальных сомнениях – не принимать подобные транзакций.
Осознавайте, что в обнаружения криминальных природы активов, пользователь с высокой вероятностью будете столкнуться с применением санкциям параллельно одновременно с плательщиком. В связи с этим целесообразнее перестраховаться и скрупулезно изучать любой транзакцию, чем рисковать личной репутацией как и быть втянутым в значительные судебные проблемы.
Поддержание осторожности в ходе взаимодействии с USDT TRC-20 – это гарантия вашей денежной сохранности наряду с защита от незаконные практики. Проявляйте внимательными и всегда проверяйте генезис электронных валютных финансов.
Hi, i believe that i saw you visited my weblog thus i got here to “go back the favor”.I’m attempting to in finding things to enhance my website!I assume its good enough to use some of your ideas!!
Название: Обязательно контролируйте адресе адресата во время транзакции USDT TRC20
В процессе взаимодействии со крипто, особенно с USDT на блокчейне TRON (TRC20), крайне важно демонстрировать бдительность и аккуратность. Единственная из числа наиболее распространенных погрешностей, какую делают пользователи – передача денег по ошибочный адрес. Для того чтобы устранить лишение собственных USDT, необходимо неизменно тщательно проверять адресе получателя перед передачей перевода.
Цифровые адреса представляют собой протяженные наборы букв и чисел, например, TRX9QahiFUYfHffieZThuzHbkndWvvfzThB8U. Даже малая ошибка или оплошность при копирования адреса кошелька может привести к тому результату, что ваши цифровые деньги будут невозвратно утрачены, поскольку они окажутся на неконтролируемый вами криптокошелек.
Существуют различные методы контроля адресов кошельков USDT TRC20:
1. Зрительная ревизия. Тщательно соотнесите адрес во своём кошельке с адресом кошелька получателя. В случае небольшом расхождении – не производите транзакцию.
2. Применение веб-инструментов контроля.
3. Двойная верификация с реципиентом. Обратитесь с просьбой к адресату заверить корректность адреса кошелька до посылкой транзакции.
4. Тестовый операция. При крупной величине транзакции, возможно предварительно передать незначительное количество USDT для контроля адреса кошелька.
Сверх того рекомендуется содержать крипто на собственных кошельках, а не в биржах или посреднических сервисах, чтобы иметь полный управление по отношению к своими ресурсами.
Не пренебрегайте удостоверением адресов при деятельности с USDT TRC20. Данная обычная мера безопасности поможет обезопасить ваши средства от случайной потери. Помните, чтобы на мире криптовалют операции необратимы, и переданные монеты по неправильный адрес кошелька вернуть фактически невозможно. Пребывайте осторожны и тщательны, чтобы защитить свои капиталовложения.
האפליקציה הינה אפליקציה רווחת בישראל לרכישת קנאביס בצורה מקוון. זו מעניקה ממשק משתמש פשוט לשימוש ובטוח לרכישה ולקבלת שילוחים מ פריטי מריחואנה שונים. במאמר זו נבחן את הרעיון שמאחורי הפלטפורמה, כיצד זו פועלת ומה המעלות מ השימוש בזו.
מה זו הפלטפורמה?
האפליקציה הווה דרך לרכישת מריחואנה באמצעות האפליקציה טלגראם. זו מבוססת מעל ערוצי תקשורת וקהילות טלגראם ספציפיות הנקראות ״טלגראס כיוונים, שם אפשר להזמין מרחב מוצרי מריחואנה ולקבל אלו ישירותית לשילוח. הערוצים אלו מסודרים על פי איזורים גיאוגרפיים, כדי לשפר על קבלת המשלוחים.
כיצד זה עובד?
התהליך קל למדי. קודם כל, יש להצטרף לערוץ טלגראס הרלוונטי לאזור המגורים. שם ניתן לעיין בתפריטים של הפריטים המגוונים ולהזמין את המוצרים המבוקשים. לאחר ביצוע ההזמנה וסגירת התשלום, השליח יגיע לכתובת שנרשמה ועמו החבילה שהוזמן.
מרבית ערוצי הטלגראס מספקים טווח נרחב של פריטים – זנים של צמח הקנאביס, ממתקים, משקאות ועוד. כמו כן, אפשר למצוא חוות דעת של לקוחות שעברו לגבי רמת הפריטים והשרות.
מעלות השימוש בטלגראס
יתרון מרכזי מ הפלטפורמה הינו הנוחיות והדיסקרטיות. ההרכבה והתהליך מתבצעות ממרחק מאיזשהו מיקום, בלי צורך בהתכנסות פיזי. בנוסף, הפלטפורמה מוגנת ביסודיות ומבטיחה חיסיון גבוהה.
מלבד אל זאת, עלויות הפריטים באפליקציה נוטים לבוא תחרותיים, והשילוחים מגיעים במהירות ובהשקעה גבוהה. קיים אף מוקד תמיכה זמין לכל שאלה או בעיית.
לסיכום
האפליקציה היא שיטה מקורית ויעילה לרכוש מוצרי קנאביס במדינה. היא משלבת בין הנוחות הטכנולוגית של היישומון הפופולרית, לבין הזריזות והדיסקרטיות של דרך השילוח הישירות. ככל שהדרישה לצמח הקנאביס גדלה, אפליקציות כמו זו צפויות להמשיך ולהתפתח.
prostatitis pills different – prostatitis treatment end pills for treat prostatitis special
Взгляд ее наполнился печалью, голова сама опустилась из-за тяжести мыслей, терзающих ее внутри. Она ничего не говорила, да и расспрос в магазине мужчину не особого интересовал в данный момент. Им понадобилось буквально полчаса, что бы собрать нужную продуктовую корзину, «правильную». Она очень отличалась от их привычной: там не было сладостей и газировки, копченостей и выпечки. Особенным ударом ниже пояса для мужчины стал отказ в покупке майонеза:
—Боже мой, что это. «Хлеб диетический», ух ты…. И ты хочешь сказать, что за эти два пакета зелени мы заплатили три тысячи?
—Так ты посмотри, сколько мы набрали? Это же не ролтон, ими наесться на весь день можно. И еще похудеть в том числе.
мужчина полностью не ожидал из уст своей супруги Татьяны. Среди их собственной родственной группе телосложение организма абсолютно отличалась в противовес нормативной и также общепринятой – иметь предожирение полная условие.
Замена венцов красноярск
Геракл24: Профессиональная Замена Основания, Венцов, Настилов и Передвижение Домов
Компания Gerakl24 занимается на предоставлении полных работ по замене основания, венцов, полов и перемещению зданий в месте Красноярском регионе и в окрестностях. Наша команда профессиональных мастеров обеспечивает превосходное качество выполнения всех видов восстановительных работ, будь то из дерева, каркасные, кирпичные или бетонные строения.
Преимущества работы с Gerakl24
Квалификация и стаж:
Все работы проводятся исключительно высококвалифицированными мастерами, имеющими многолетний опыт в направлении создания и восстановления строений. Наши сотрудники знают свое дело и осуществляют работу с безупречной точностью и вниманием к деталям.
Комплексный подход:
Мы предоставляем все виды работ по ремонту и ремонту домов:
Замена фундамента: усиление и реставрация старого основания, что обеспечивает долгий срок службы вашего строения и предотвратить проблемы, вызванные оседанием и деформацией.
Смена венцов: замена нижних венцов деревянных домов, которые наиболее часто гниют и разрушаются.
Замена полов: замена старых полов, что существенно улучшает внешний вид и функциональные характеристики.
Перемещение зданий: безопасное и надежное перемещение зданий на другие участки, что обеспечивает сохранение строения и предотвращает лишние расходы на возведение нового.
Работа с любыми типами домов:
Древесные строения: реставрация и усиление деревянных элементов, обработка от гниения и насекомых.
Каркасные строения: укрепление каркасов и реставрация поврежденных элементов.
Кирпичные дома: восстановление кирпичной кладки и усиление стен.
Бетонные дома: восстановление и укрепление бетонных структур, ремонт трещин и дефектов.
Качество и надежность:
Мы применяем только высококачественные материалы и новейшее оборудование, что гарантирует долгий срок службы и прочность всех выполненных задач. Все проекты подвергаются строгому контролю качества на всех этапах выполнения.
Личный подход:
Каждому клиенту мы предлагаем персонализированные решения, учитывающие все особенности и пожелания. Мы стараемся, чтобы итог нашей работы полностью удовлетворял вашим запросам и желаниям.
Почему выбирают Геракл24?
Обратившись к нам, вы найдете надежного партнера, который возьмет на себя все заботы по ремонту и реставрации вашего дома. Мы обещаем выполнение всех проектов в установленные сроки и с соблюдением всех строительных норм и стандартов. Связавшись с Геракл24, вы можете быть уверены, что ваш дом в надежных руках.
Мы предлагаем консультацию и ответить на ваши вопросы. Контактируйте с нами, чтобы обсудить детали и узнать больше о наших услугах. Мы сохраним и улучшим ваш дом, сделав его уютным и безопасным для долгого проживания.
Gerakl24 – ваш партнер по реставрации и ремонту домов в Красноярске и окрестностях.
??????????The Dubrovskys family was again roaming the supermarket in full force, looking for snacks or something tasty. The head of the family, Paul, a 40-year-old overweight man, again turned his attention to the chip shelves:
— Masha, let’s take these? I’ve never tried with salted gherkins before, it’s a new product!
— Yes, let’s get them!
valtrex online dizzy – valtrex fright valacyclovir online oil
ברוכים הנכנסים לפורטל הידע והמידע והתרומה הרשמי של טלגראס אופקים! בנקודה זו תוכלו למצוא את כל הנתונים והמידע העדכני והמעודכן הזמין ביותר לגבי מערכת טלגרף והדרכים להפעלתה בצורה נכונה.
מה הוא טלגרם אופקים?
טלגרם כיוונים היא מערכת הנשענת על טלגרם המשמשת להפצה ורכישה סביב דשא ודשא בתחום. באמצעות ההודעות והחוגים בטלגרף, לקוחות רשאים לרכוש ולהשיג אספקת קנאביס באופן קל ומהיר.
באיזה דרך להשתלב בפלטפורמת טלגרם?
לשם להיכנס בשימוש נכון בטלגראס כיוונים, עליכם להתחבר ל לקבוצות ולפורומים המאומתים. במקום במאגר זה תוכלו לאתר סיכום עבור קישורים לשיחות מעורבים וראויים. בהמשך, תוכלו להתחבר בפעילות הקבלה וההספקה סביב אספקת המריחואנה.
מידע ומידע
במקום הנוכחי אפשר למצוא מבחר מתוך מפרטים וכללים ברורים בנוגע ל השילוב בפלטפורמת טלגרם, כולל:
– החברות למקומות איכותיים
– שלבי ההזמנה
– אבטחה והאמינות בשימוש בפלטפורמת טלגרם
– והרבה מידע נוסף בנוסף
קישורים מאומתים
לגבי נושא זה צירים לשיחות ולקבוצות רצויים בפלטפורמת טלגרם:
– ערוץ המידע המוכר
– קבוצת הסיוע והעזרה לצרכנים
– פורום לאספקת מוצרי קנאביס מובטחים
– מדריך נקודות קנאביס מוטבחות
מערך מברכים אתם עקב הפעילות שלכם לפורטל המידע והנתונים עבור טלגרף כיוונים ומייחלים לכם חווית שהיא קנייה מרוצה ובטוחה!
claritin pills grant – loratadine foreign claritin pills since
Геракл24: Профессиональная Замена Основания, Венцов, Настилов и Перенос Строений
Организация Геракл24 занимается на предоставлении полных работ по замене фундамента, венцов, настилов и передвижению строений в месте Красноярском регионе и в окрестностях. Наш коллектив профессиональных специалистов обещает высокое качество исполнения различных типов ремонтных работ, будь то деревянные, каркасного типа, кирпичные постройки или бетонные здания.
Плюсы сотрудничества с Геракл24
Навыки и знания:
Каждая задача осуществляются лишь опытными специалистами, имеющими большой стаж в области создания и восстановления строений. Наши сотрудники профессионалы в своем деле и осуществляют проекты с высочайшей точностью и вниманием к мелочам.
Комплексный подход:
Мы предлагаем разнообразные услуги по реставрации и реконструкции строений:
Замена фундамента: замена и укрепление фундамента, что обеспечивает долгий срок службы вашего строения и избежать проблем, связанные с оседанием и деформацией.
Смена венцов: реставрация нижних венцов из дерева, которые обычно гниют и разрушаются.
Замена полов: замена старых полов, что значительно улучшает внешний вид и функциональность помещения.
Перенос строений: качественный и безопасный перенос строений на новые локации, что обеспечивает сохранение строения и избежать дополнительных затрат на создание нового.
Работа с любыми типами домов:
Дома из дерева: реставрация и усиление деревянных элементов, защита от гниения и вредителей.
Каркасные строения: реставрация каркасов и замена поврежденных элементов.
Кирпичные строения: реставрация кирпичной кладки и укрепление конструкций.
Бетонные дома: ремонт и укрепление бетонных конструкций, исправление трещин и разрушений.
Качество и прочность:
Мы применяем только высококачественные материалы и новейшее оборудование, что гарантирует долговечность и надежность всех работ. Все проекты подвергаются строгому контролю качества на всех этапах выполнения.
Персонализированный подход:
Каждому клиенту мы предлагаем подходящие решения, учитывающие ваши требования и желания. Наша цель – чтобы конечный результат соответствовал ваши ожидания и требования.
Почему выбирают Геракл24?
Сотрудничая с нами, вы приобретете надежного партнера, который возьмет на себя все хлопоты по восстановлению и ремонту вашего здания. Мы обещаем выполнение всех проектов в сроки, оговоренные заранее и с соблюдением всех правил и норм. Обратившись в Геракл24, вы можете не сомневаться, что ваш дом в надежных руках.
Мы готовы предоставить консультацию и ответить на ваши вопросы. Свяжитесь с нами, чтобы обсудить ваш проект и узнать о наших сервисах. Мы сохраним и улучшим ваш дом, сделав его уютным и безопасным для долгого проживания.
Gerakl24 – ваш партнер по реставрации и ремонту домов в Красноярске и окрестностях.
Tonic Greens: An Overview. Introducing Tonic Greens, an innovative immune support supplement
Keep working ,great job!
loratadine medication lake – claritin pills entity claritin pills stumble
What Is LeanBiome? LeanBiome, a new weight loss solution, includes beneficial strains of gut bacteria that work fast for weight loss.
What Is ErecPrime? ErecPrime is a male enhancement supplement that will help with improving one’s sexual experience.
priligy lofty – dapoxetine bloody dapoxetine weary
Yeah bookmaking this wasn’t a bad determination outstanding post! .
Работая в сео, нужно понимать, что нельзя одним методом продвинуть веб-сайт в топ выдачи поисковиков, поскольку системы поиска это как трек с финишной линией, а сайты это гоночные автомобили, которые все желают быть первыми.
Так вот:
Перечень – Для того чтобы веб-сайт был адаптивным и быстр, важна
оптимизирование
Сайт должен иметь только уникальные материалы, это текст и картинки
ОБЯЗАТЕЛЬНО ссылочный профиль через сайты статейники и напрямую на главную страницу
Укрепление беклинков с помощью второстепенных сайтов
Ссылочная структура, эти ссылки Tier-1, Tier-2, Tier-3
А главное это личная сеть веб-сайтов PBN, которая подключается на деньговый сайт
Все PBN-сайты должны быть без следов, т.е. системы поиска не должны понимать, что это один владелец всех веб-сайтов, поэтому крайне важно соблюдать все эти указания.
娛樂城
線上娛樂城的天地
隨著互聯網的快速發展，在線娛樂城（在線賭場）已經成為許多人娛樂的新選擇。網上娛樂城不僅提供多種的游戲選擇，還能讓玩家在家中就能體驗到賭場的刺激和樂趣。本文將討論在線娛樂城的特點、優勢以及一些常有的游戲。
什麼在線娛樂城？
在線娛樂城是一種經由互聯網提供賭錢遊戲的平台。玩家可以通過計算機、智慧型手機或平板電腦進入這些網站，參與各種賭博活動，如撲克牌、賭盤、21點和老虎機等。這些平台通常由專家的軟件公司開發，確保游戲的公平性和安全性。
網上娛樂城的好處
便利性：玩家不用離開家，就能享受博彩的快感。這對於那些生活在遠離實體賭場地區的人來說尤為方便。
多樣化的遊戲選擇：線上娛樂城通常提供比實體賭場更多樣化的游戲選擇，並且經常更新游戲內容，保持新鮮。
優惠和獎金：許多線上娛樂城提供多樣的獎勵計劃，包括註冊紅利、存款獎勵和忠誠計劃，吸引新新玩家並激勵老玩家繼續遊戲。
穩定性和保密性：正規的網上娛樂城使用高端的加密方法來保護玩家的個人信息和財務交易，確保遊戲過程的公平和公正。
常有的在線娛樂城遊戲
撲克：撲克牌是最流行賭博遊戲之一。在線娛樂城提供各種撲克變體，如德州撲克、奧馬哈和七張牌撲克等。
輪盤賭：賭盤是一種傳統的賭場遊戲，玩家可以賭注在單個數字、數字排列或顏色上，然後看小球落在哪個位置。
黑傑克：又稱為黑傑克，這是一種競爭玩家和莊家點數點數的游戲，目標是讓手牌點數盡可能接近21點但不超過。
吃角子老虎：老虎機是最受歡迎且是最流行的博彩遊戲之一，玩家只需轉動捲軸，等待圖案排列出贏得的組合。
結論
線上娛樂城為當代賭博愛好者提供了一個方便、興奮且多元化的娛樂活動。不論是撲克愛好者還是吃角子老虎迷，大家都能在這些平台上找到適合自己的游戲。同時，隨著科技的不斷進步，網上娛樂城的游戲體驗將變得越來越越來越逼真和吸引人。然而，玩家在享受遊戲的同時，也應該自律，避免沉迷於賭博活動，保持健康的心態。
娛樂城
在線娛樂城的世界
隨著互聯網的快速發展，線上娛樂城（網上賭場）已經成為許多人娛樂的新選擇。在線娛樂城不僅提供多種的遊戲選擇，還能讓玩家在家中就能體驗到賭場的樂趣和樂趣。本文將探討網上娛樂城的特色、優勢以及一些常有的游戲。
什麼是在線娛樂城？
線上娛樂城是一種透過網際網路提供賭錢游戲的平台。玩家可以透過計算機、智能手機或平板進入這些網站，參與各種賭博活動，如德州撲克、輪盤、二十一點和老虎机等。這些平台通常由專家的軟件公司開發，確保游戲的公正和安全。
在線娛樂城的利益
便利：玩家不需要離開家，就能享用博彩的樂趣。這對於那些住在在遠離的實體賭場地區的人來說尤其方便。
多元化的游戲選擇：網上娛樂城通常提供比實體賭場更豐富的遊戲選擇，並且經常升級遊戲內容，保持新穎。
福利和獎金：許多網上娛樂城提供豐厚的優惠計劃，包括註冊獎金、存款獎金和忠誠計劃，引誘新玩家並促使老玩家不斷遊戲。
穩定性和隱私性：合法的網上娛樂城使用先進的的加密技術來保護玩家的私人信息和交易，確保游戲過程的穩定和公正。
常見的的線上娛樂城游戲
撲克牌：撲克是最流行賭博遊戲之一。網上娛樂城提供多種德州撲克變體，如德州扑克、奧馬哈撲克和七張牌等。
賭盤：賭盤是一種傳統的賭場遊戲遊戲，玩家可以賭注在數字、數字組合或顏色上上，然後看球落在哪個地方。
二十一點：又稱為21點，這是一種比拼玩家和莊家點數點數的遊戲，目標是讓手牌點數點數儘量接近21點但不超過。
老虎机：老虎机是最簡單且是最流行的賭錢游戲之一，玩家只需旋轉捲軸，看圖案排列出贏得的組合。
結論
網上娛樂城為當代賭博愛好者提供了一個便捷、刺激且豐富的娛樂選擇。不論是撲克牌愛好者還是吃角子老虎迷，大家都能在這些平台上找到適合自己的游戲。同時，隨著技術的不斷提升，線上娛樂城的游戲體驗將變得越來越越來越逼真和引人入勝。然而，玩家在享用游戲的同時，也應該自律，避免沉溺於賭錢活動，保持健康的心態。
promethazine greater – promethazine mortal promethazine farewell
sapporo88
sapporo88
Explore Thrilling Promotions and Bonus Spins: Your Definitive Guide
At our gaming platform, we are dedicated to providing you with the best gaming experience possible. Our range of promotions and free spins ensures that every player has the chance to enhance their gameplay and increase their chances of winning. Here’s how you can take advantage of our amazing promotions and what makes them so special.
Plentiful Extra Spins and Rebate Promotions
One of our standout offers is the opportunity to earn up to 200 free spins and a 75% cashback with a deposit of just $20 or more. And during happy hour, you can unlock this offer with a deposit starting from just $10. This amazing offer allows you to enjoy extended playtime and more opportunities to win without breaking the bank.
Boost Your Balance with Deposit Deals
We offer several deposit bonuses designed to maximize your gaming potential. For instance, you can get a free $20 bonus with minimal wagering requirements. This means you can start playing with extra funds, giving you more chances to explore our vast array of games and win big. Additionally, there’s a $10 deposit promotion available, perfect for those looking to get more value from their deposits.
Multiply Your Deposits for Bigger Wins
Our “Play Big!” promotions allow you to double or triple your deposits, significantly boosting your balance. Whether you choose to multiply your deposit by 2 or 3 times, these offers provide you with a substantial amount of extra funds to enjoy. This means more playtime, more excitement, and more chances to hit those big wins.
Exciting Free Spins on Popular Games
We also offer up to 1000 free spins per deposit on some of the most popular games in the industry. Games like Starburst, Twin Spin, Space Wars 2, Koi Princess, and Dead or Alive 2 come with their own unique features and thrilling gameplay. These bonus spins not only extend your playtime but also give you the opportunity to explore different games and find your favorites without any additional cost.
Why Choose Our Platform?
Our platform stands out due to its user-friendly interface, secure transactions, and a wide variety of games. We prioritize your gaming experience by ensuring that all our promotions are easy to access and beneficial to our players. Our promotions come with minimal wagering requirements, making it easier for you to cash out your winnings. Moreover, the variety of games we offer ensures that there’s something for every type of player, from classic slot enthusiasts to those who enjoy more modern, feature-packed games.
Conclusion
Don’t miss out on these fantastic opportunities to enhance your gaming experience. Whether you’re looking to enjoy free spins, cashback, or plentiful deposit promotions, we have something for everyone. Join us today, take advantage of these amazing offers, and start your journey to big wins and endless fun. Happy gaming!
video games guide
Thrilling Breakthroughs and Popular Releases in the World of Gaming
In the dynamic realm of digital entertainment, there’s constantly something fresh and exciting on the brink. From enhancements enhancing revered staples to anticipated releases in renowned series, the digital entertainment realm is as vibrant as before.
Let’s take a glimpse into the most recent updates and certain the most popular games enthralling players across the globe.
Newest Announcements
1. Innovative Enhancement for Skyrim Optimizes Non-Player Character Visuals
A recent mod for The Elder Scrolls V: Skyrim has grabbed the focus of fans. This modification implements detailed faces and dynamic hair for each non-player characters, improving the world’s aesthetics and depth.
2. Total War Series Game Placed in Star Wars Universe in Development
Creative Assembly, famous for their Total War Series collection, is reportedly working on a forthcoming game set in the Star Wars Galaxy world. This exciting collaboration has gamers looking forward to the profound and immersive gameplay that Total War releases are known for, ultimately set in a universe distant.
3. GTA VI Arrival Announced for Late 2025
Take-Two’s CEO’s Head has announced that Grand Theft Auto VI is expected to arrive in Late 2025. With the overwhelming popularity of its prior release, Grand Theft Auto V, gamers are excited to explore what the future installment of this renowned universe will deliver.
4. Enlargement Plans for Skull & Bones Second Season
Designers of Skull and Bones have announced amplified plans for the experience’s Season Two. This nautical experience delivers fresh updates and updates, keeping gamers immersed and engrossed in the realm of oceanic swashbuckling.
5. Phoenix Labs Studio Faces Staff Cuts
Regrettably, not everything news is good. Phoenix Labs, the creator in charge of Dauntless Game, has announced significant personnel cuts. Despite this challenge, the experience continues to be a beloved preference among enthusiasts, and the studio continues to be committed to its community.
Popular Experiences
1. Wild Hunt
With its engaging plot, captivating domain, and enthralling experience, The Witcher 3: Wild Hunt continues to be a cherished release across fans. Its deep narrative and expansive nonlinear world keep to draw enthusiasts in.
2. Cyberpunk 2077
Despite a rocky release, Cyberpunk continues to be a long-awaited release. With ongoing enhancements and optimizations, the release continues to evolve, providing gamers a perspective into a high-tech environment abundant with danger.
3. GTA V
Still time following its original launch, Grand Theft Auto 5 stays a renowned selection amidst players. Its wide-ranging open world, compelling narrative, and co-op components keep enthusiasts revisiting for ongoing explorations.
4. Portal 2 Game
A legendary analytical game, Portal is renowned for its pioneering gameplay mechanics and brilliant map design. Its demanding obstacles and clever writing have cemented it as a remarkable title in the interactive entertainment world.
5. Far Cry
Far Cry 3 is praised as exceptional games in the franchise, providing enthusiasts an free-roaming exploration rife with danger. Its immersive story and legendary entities have established its standing as a fan favorite experience.
6. Dishonored Series
Dishonored Game is celebrated for its covert features and distinctive world. Gamers take on the role of a otherworldly executioner, exploring a city filled with societal danger.
7. Assassin’s Creed Game
As a component of the acclaimed Assassin’s Creed Franchise series, Assassin’s Creed Game is adored for its immersive story, engaging mechanics, and time-period environments. It stays a standout game in the collection and a beloved amidst enthusiasts.
In summary, the domain of gaming is prospering and ever-changing, with groundbreaking developments
भारत में ऑनलाइन क्रिकेट सट्टेबाजी की बढ़ती लोकप्रियता
भारत में क्रिकेट को एक धर्म के रूप में देखा जाता है। क्रिकेट के प्रति भारतीयों की अटूट प्रेम और उत्साह को देखते हुए, ऑनलाइन क्रिकेट सट्टेबाजी ने पिछले कुछ वर्षों में जबरदस्त लोकप्रियता हासिल की है।
इस लोकप्रियता के पीछे कुछ प्रमुख कारण हैं। सबसे पहले, बेटवीसा जैसे विश्वसनीय ऑनलाइन कैसीनो और खेल प्लेटफॉर्मों के आगमन ने ऑनलाइन क्रिकेट सट्टेबाजी को एक नया आयाम प्रदान किया है। बेटवीसा भारत में एक प्रमुख खिलाड़ी है, जो अपने कुराकाओ गेमिंग लाइसेंस और 2 मिलियन से अधिक उपयोगकर्ताओं के साथ एक विश्वसनीय और सुरक्षित प्लेटफॉर्म प्रदान करता है।
दूसरा, बेटवीसा ऐप और बेटवीसा लॉगिन प्रक्रिया की सरलता ने उपयोगकर्ताओं को अपने मोबाइल डिवाइसों से क्रिकेट सट्टेबाजी करने में सक्षम बनाया है। इससे उन्हें कहीं से भी खेलने की सुविधा मिलती है।
साथ ही, बेटवीसा जैसे प्लेटफॉर्मों ने विविध भुगतान विकल्प और सुरक्षित लेनदेन की पेशकश की है, जिससे उपयोगकर्ताओं को एक विश्वसनीय और आरामदायक अनुभव प्राप्त होता है।
समग्र रूप से, भारत में ऑनलाइन क्रिकेट सट्टेबाजी की बढ़ती लोकप्रियता में बेटवीसा जैसे प्रमुख ऑनलाइन कैसीनो और खेल प्लेटफॉर्मों की महत्वपूर्ण भूमिका है। इनके आसान, सुरक्षित और विश्वसनीय प्लेटफॉर्म ने क्रिकेट प्रेमियों को एक नया और उत्साहजनक गेमिंग अनुभव प्रदान किया है।
Betvisa Bet
Betvisa Bet | Catch the BPL Excitement with Betvisa!
Hunt for ₹10million! | Enter the BPL at Betvisa and chase a staggering Bounty.
Valentine’s Boost at Visa Bet! | Feel the rush of a 143% Love Mania Bonus .
predict BPL T20 outcomes | score big rewards through Betvisa login!
#betvisa
Betvisa bonus Win! | Leverage your 10 free spins to possibly win $8,888.
Share and Earn! | win ₹500 via the Betvisa app download!
https://www.betvisa-bet.com/hi
#visabet #betvisalogin #betvisaapp #betvisaIndia
Sign-Up Jackpot! | Register at Betvisa India and win ₹8,888.
Double your play! | with a ₹1,000 deposit and get ₹2,000 free at Betvisa online!
Download the Betvisa download today and don’t miss out on the action!
ascorbic acid inside – ascorbic acid rot ascorbic acid chimney
Discover Stimulating Offers and Bonus Spins: Your Comprehensive Guide
At our gaming platform, we are committed to providing you with the best gaming experience possible. Our range of deals and free spins ensures that every player has the chance to enhance their gameplay and increase their chances of winning. Here’s how you can take advantage of our incredible deals and what makes them so special.
Lavish Extra Spins and Rebate Deals
One of our standout promotions is the opportunity to earn up to 200 bonus spins and a 75% rebate with a deposit of just $20 or more. And during happy hour, you can unlock this bonus with a deposit starting from just $10. This incredible promotion allows you to enjoy extended playtime and more opportunities to win without breaking the bank.
Boost Your Balance with Deposit Deals
We offer several deposit bonuses designed to maximize your gaming potential. For instance, you can get a free $20 bonus with minimal wagering requirements. This means you can start playing with extra funds, giving you more chances to explore our vast array of games and win big. Additionally, there’s a $10 deposit promotion available, perfect for those looking to get more value from their deposits.
Multiply Your Deposits for Bigger Wins
Our “Play Big!” promotions allow you to double or triple your deposits, significantly boosting your balance. Whether you choose to multiply your deposit by 2 or 3 times, these offers provide you with a substantial amount of extra funds to enjoy. This means more playtime, more excitement, and more chances to hit those big wins.
Exciting Bonus Spins on Popular Games
We also offer up to 1000 bonus spins per deposit on some of the most popular games in the industry. Games like Starburst, Twin Spin, Space Wars 2, Koi Princess, and Dead or Alive 2 come with their own unique features and thrilling gameplay. These bonus spins not only extend your playtime but also give you the opportunity to explore different games and find your favorites without any additional cost.
Why Choose Our Platform?
Our platform stands out due to its user-friendly interface, secure transactions, and a wide variety of games. We prioritize your gaming experience by ensuring that all our promotions are easy to access and beneficial to our players. Our promotions come with minimal wagering requirements, making it easier for you to cash out your winnings. Moreover, the variety of games we offer ensures that there’s something for every type of player, from classic slot enthusiasts to those who enjoy more modern, feature-packed games.
Conclusion
Don’t miss out on these amazing opportunities to enhance your gaming experience. Whether you’re looking to enjoy free spins, refund, or plentiful deposit promotions, we have something for everyone. Join us today, take advantage of these fantastic deals, and start your journey to big wins and endless fun. Happy gaming!
Key Factors for Success: Enhancing Your Experience on Betvisa Login Sites in 2024
As the world of online gambling continues to evolve at a rapid pace, it’s essential for players to stay ahead of the curve and adapt their strategies accordingly. Whether you’re a seasoned player or just starting your journey, keeping a keen eye on the key factors that can enhance your online gambling experience is crucial, especially when navigating platforms like Betvisa Login.
Prioritizing Secure and Trusted Platforms
In the ever-changing landscape of online gambling, selecting a reputable and trustworthy platform is the foundation for a successful and enjoyable experience. Betvisa Login has established itself as a leading destination, renowned for its commitment to player safety, secure transactions, and robust licensing and regulation. By choosing platforms like Betvisa Login, you can rest assured that your personal and financial information is protected, allowing you to focus on the thrill of the game.
Mastering Game Strategies
The diverse range of games available on Betvisa Login platforms requires a deeper understanding of the underlying strategies and mechanics. From the nuances of Visa Bet to the intricacies of the Betvisa Casino offerings, taking the time to familiarize yourself with the rules, payouts, and winning techniques can significantly improve your chances of success. Utilize free demo versions and educational resources to hone your skills before diving into real-money play.
Capitalizing on Bonuses and Promotions
Online gambling platforms, including Betvisa Login, often offer a range of bonuses and promotions to attract and retain players. From welcome bonuses to free spins and reload offers, these incentives can provide you with valuable extra funds to explore the platform’s offerings. However, it’s crucial to read the terms and conditions carefully to ensure you maximize the potential benefits and avoid any unintended consequences.
Maintaining a Balanced Approach
Responsible gambling practices are essential for a sustainable and enjoyable online gambling experience. Betvisa Login encourages players to set and adhere to personal limits on both time and financial resources. By maintaining a balanced approach, you can ensure that your online gambling activities remain a source of entertainment rather than a source of stress or financial burden.
Staying Informed and Adaptable
The online gambling landscape is constantly evolving, with new games, regulations, and industry trends emerging on a regular basis. To stay ahead of the curve, it’s crucial to stay informed about the latest developments. Follow industry news, join online communities, and subscribe to Betvisa Login’s communication channels to ensure you’re always up-to-date on the latest opportunities and best practices.
Leveraging Customer Support
When navigating the complexities of online gambling, having access to reliable and responsive customer support can make a significant difference. Betvisa Login’s support team is dedicated to addressing player inquiries and resolving any issues that may arise, ensuring a seamless and stress-free experience.
As we usher in the new year, 2024 promises to be an exciting time for online gambling enthusiasts. By focusing on the key factors outlined above and leveraging the robust offerings of platforms like Betvisa Login, players can elevate their online gambling experience, maximize their chances of success, and embrace the thrilling opportunities that lie ahead.
Betvisa Bet | Step into the Arena with Betvisa!
Spin to Win Daily at Betvisa PH! | Take a whirl and bag ₱8,888 in big rewards.
Valentine’s 143% Love Boost at Visa Bet! | Celebrate romance and rewards !
Deposit Bonus Magic! | Deposit 50 and get an 88 bonus instantly at Betvisa Casino.
#betvisa
Free Cash & More Spins! | Sign up betvisa login,grab 500 free cash plus 5 free spins.
Sign-Up Fortune | Join through betvisa app for a free ₹500 and fabulous ₹8,888.
https://www.betvisa-bet.com/tl
#visabet #betvisalogin #betvisacasino # betvisaph
Double Your Play at betvisa com! | Deposit 1,000 and get a whopping 2,000 free
100% Cock Fight Welcome at Visa Bet! | Plunge into the exciting world .Bet and win!
Jump into Betvisa for exciting games, stunning bonuses, and endless winnings!
Discover Thrilling Offers and Free Spins: Your Definitive Guide
At our gaming platform, we are focused to providing you with the best gaming experience possible. Our range of deals and bonus spins ensures that every player has the chance to enhance their gameplay and increase their chances of winning. Here’s how you can take advantage of our amazing deals and what makes them so special.
Lavish Bonus Spins and Refund Offers
One of our standout promotions is the opportunity to earn up to 200 bonus spins and a 75% refund with a deposit of just $20 or more. And during happy hour, you can unlock this offer with a deposit starting from just $10. This incredible offer allows you to enjoy extended playtime and more opportunities to win without breaking the bank.
Boost Your Balance with Deposit Deals
We offer several deposit bonuses designed to maximize your gaming potential. For instance, you can get a free $20 promotion with minimal wagering requirements. This means you can start playing with extra funds, giving you more chances to explore our vast array of games and win big. Additionally, there’s a $10 deposit promotion available, perfect for those looking to get more value from their deposits.
Multiply Your Deposits for Bigger Wins
Our “Play Big!” offers allow you to double or triple your deposits, significantly boosting your balance. Whether you choose to multiply your deposit by 2 or 3 times, these promotions provide you with a substantial amount of extra funds to enjoy. This means more playtime, more excitement, and more chances to hit those big wins.
Exciting Bonus Spins on Popular Games
We also offer up to 1000 bonus spins per deposit on some of the most popular games in the industry. Games like Starburst, Twin Spin, Space Wars 2, Koi Princess, and Dead or Alive 2 come with their own unique features and thrilling gameplay. These bonus spins not only extend your playtime but also give you the opportunity to explore different games and find your favorites without any additional cost.
Why Choose Our Platform?
Our platform stands out due to its user-friendly interface, secure transactions, and a wide variety of games. We prioritize your gaming experience by ensuring that all our offers are easy to access and beneficial to our players. Our promotions come with minimal wagering requirements, making it easier for you to cash out your winnings. Moreover, the variety of games we offer ensures that there’s something for every type of player, from classic slot enthusiasts to those who enjoy more modern, feature-packed games.
Conclusion
Don’t miss out on these incredible opportunities to enhance your gaming experience. Whether you’re looking to enjoy bonus spins, cashback, or plentiful deposit promotions, we have something for everyone. Join us today, take advantage of these awesome offers, and start your journey to big wins and endless fun. Happy gaming!
JiliAce ক্যাসিনোতে অনলাইন মোরগ লড়াই এবং রেসিং গেম: একটি নতুন অভিজ্ঞতা
অনলাইন গেমিংয়ের বিশ্বে JiliAce ক্যাসিনো একটি বিশেষ স্থান অধিকার করে নিয়েছে, যেখানে ব্যবহারকারীরা বিভিন্ন ধরনের গেম উপভোগ করতে পারেন। আজ আমরা JiliAce〡JitaBet প্ল্যাটফর্মে পাওয়া দুটি জনপ্রিয় গেম সম্পর্কে জানবো: অনলাইন মোরগ লড়াই এবং রেসিং গেম।
অনলাইন মোরগ লড়াই: ঐতিহ্যবাহী গেমের ডিজিটাল রূপ
মোরগ লড়াই হল একটি অনলাইন গেম যা পন্টারদের বিভিন্ন প্রতিযোগী ডিজিটাল মোরগগুলিতে বাজি রাখার ক্ষমতা দেয়। ঐতিহ্যগতভাবে, মোরগ লড়াই একটি জনপ্রিয় খেলা ছিল, যেখানে মোরগদের মধ্যে প্রতিযোগিতা হতো। এখন এই গেমটি অনলাইনে খেলা যায়, যেখানে আপনি আপনার পছন্দের মোরগের উপর বাজি রাখতে পারেন এবং উত্তেজনাপূর্ণ প্রতিযোগিতার অভিজ্ঞতা উপভোগ করতে পারেন। Jili ace casino-তে এই গেমটি খেলে আপনি ঐতিহ্যবাহী মোরগ লড়াইয়ের মজার অভিজ্ঞতা পাবেন, যা ডিজিটাল প্ল্যাটফর্মে খেলার সুবিধা নিয়ে আসে।
অনলাইন রেসিং: স্পিড এবং উত্তেজনার মিশ্রণ
“অনলাইনে রেসিং” রেসিং সম্পর্কিত বিভিন্ন অনলাইন ক্রিয়াকলাপকে উল্লেখ করতে পারে এবং প্রসঙ্গটি নির্ভর করে নির্দিষ্ট ধরণের রেসিংয়ের উপর। JiliAce ক্যাসিনোতে, আপনি বিভিন্ন ধরনের রেসিং গেম খুঁজে পাবেন, যেখানে আপনি গাড়ি, বাইক এবং অন্যান্য যানবাহনের প্রতিযোগিতায় অংশ নিতে পারবেন। রেসিং গেমগুলি তাদের বাস্তবসম্মত গ্রাফিক্স এবং উত্তেজনাপূর্ণ গেমপ্লের জন্য পরিচিত, যা আপনাকে একটি শ্বাসরুদ্ধকর অভিজ্ঞতা প্রদান করবে। Jili ace casino-তে রেসিং গেম খেলে আপনি স্পিড এবং উত্তেজনার মিশ্রণ উপভোগ করতে পারবেন।
সহজ লগইন এবং সুবিধাজনক গেমিং
Jili ace login প্রক্রিয়া অত্যন্ত সহজ এবং ব্যবহারকারীদের জন্য সুবিধাজনক। একবার লগইন করলে, আপনি সহজেই বিভিন্ন গেমের অ্যাক্সেস পাবেন এবং আপনার পছন্দসই গেম খেলার জন্য প্রস্তুত হয়ে যাবেন। Jiliace login করার পর, আপনি আপনার গেমিং যাত্রা শুরু করতে পারবেন এবং বিভিন্ন ধরনের বোনাস ও পুরস্কার উপভোগ করতে পারবেন।
Jita Bet: বড় পুরস্কারের সুযোগ
JiliAce ক্যাসিনোতে Jita Bet-এর সাথে আপনার গেমিং অভিজ্ঞতা আরও সমৃদ্ধ করুন। এখানে আপনি বিভিন্ন ধরণের বাজি ধরতে পারেন এবং বড় পুরস্কার জিততে পারেন। Jita Bet প্ল্যাটফর্মটি ব্যবহারকারীদের জন্য সহজ এবং সুরক্ষিত বাজি ধরার সুযোগ প্রদান করে।
যোগদান করুন এবং উপভোগ করুন
JiliAce〡JitaBet-এর অংশ হয়ে আজই আপনার গেমিং যাত্রা শুরু করুন। Jili ace casino এবং Jita Bet-এ লগইন করে অনলাইন মোরগ লড়াই এবং রেসিং গেমের মত আকর্ষণীয় গেম উপভোগ করুন। এখনই যোগ দিন এবং অনলাইন গেমিংয়ের এক নতুন জগতে প্রবেশ করুন!
Jiliacet casino
Jiliacet casino |
Warm welcome! | Get a 200% Welcome Bonus when you log in jiliace casino.
IPL Tournament! | Join the IPL fever with Jita Bet. Win big prizes!
Epic JILI Tournaments! | Go head-to-head in the Jita bet Super Tournament
#jiliacecasino
Cashback on Deposits! | Get cash back on every deposit. At Jili ace casino
Uninterrupted bonuses at JITAACE! | Stay logged in Jiliace login!
https://www.jiliace-casino.online/bn
#Jiliacecasino # Jiliacelogin#Jiliacelogin # Jitabet
Slot Feast! | Spin to win 100% up to 20,000 ৳. at Jili ace login!
Big Fishing Bonus! | Get a 100% bonus up to ৳20,000 in the Fishing Game.
JiliAce Casino’s top choice for great bonuses. login, play, and win big today!
game reviews
Thrilling Developments and Iconic Franchises in the Domain of Gaming
In the dynamic environment of videogames, there’s always something fresh and engaging on the brink. From customizations enhancing iconic timeless titles to anticipated debuts in renowned franchises, the digital entertainment ecosystem is prospering as in recent memory.
We’ll take a look into the up-to-date developments and certain the most popular games mesmerizing fans globally.
Most Recent News
1. Cutting-Edge Enhancement for Skyrim Optimizes NPC Look
A freshly-launched modification for The Elder Scrolls V: Skyrim has captured the interest of fans. This mod brings detailed heads and hair physics for every supporting characters, improving the game’s graphics and depth.
2. Total War Series Title Located in Star Wars Setting Realm Under Development
Creative Assembly, renowned for their Total War Series collection, is allegedly developing a anticipated experience set in the Star Wars Galaxy realm. This exciting integration has fans eagerly anticipating the strategic and immersive adventure that Total War games are celebrated for, at last situated in a universe expansive.
3. Grand Theft Auto VI Arrival Communicated for Autumn 2025
Take-Two Interactive’s CEO has communicated that Grand Theft Auto VI is scheduled to launch in Q4 2025. With the enormous reception of its earlier title, GTA V, enthusiasts are anticipating to see what the future sequel of this celebrated franchise will deliver.
4. Extension Initiatives for Skull & Bones 2nd Season
Creators of Skull and Bones have revealed amplified initiatives for the title’s second season. This swashbuckling adventure delivers upcoming updates and enhancements, maintaining gamers engaged and immersed in the realm of oceanic piracy.
5. Phoenix Labs Studio Experiences Personnel Cuts
Disappointingly, not every news is favorable. Phoenix Labs Developer, the team responsible for Dauntless Experience, has communicated substantial staff cuts. Notwithstanding this difficulty, the game continues to be a iconic selection within enthusiasts, and the studio continues to be committed to its playerbase.
Iconic Releases
1. The Witcher 3: Wild Hunt
With its engaging experience, absorbing universe, and captivating journey, The Witcher 3: Wild Hunt keeps a revered release among fans. Its expansive plot and expansive nonlinear world remain to engage fans in.
2. Cyberpunk 2077 Game
Regardless of a rocky debut, Cyberpunk 2077 Game continues to be a much-anticipated title. With persistent improvements and adjustments, the release maintains evolve, offering enthusiasts a perspective into a dystopian environment filled with intrigue.
3. GTA 5
Still decades after its debut debut, GTA V keeps a popular preference within gamers. Its sprawling nonlinear world, compelling narrative, and multiplayer features continue to draw enthusiasts coming back for further adventures.
4. Portal 2
A renowned puzzle title, Portal is praised for its revolutionary mechanics and ingenious level design. Its intricate challenges and humorous writing have made it a exceptional title in the digital entertainment world.
5. Far Cry 3 Game
Far Cry 3 is celebrated as one of the best entries in the franchise, providing fans an sandbox exploration teeming with excitement. Its captivating story and memorable figures have established its standing as a iconic title.
6. Dishonored
Dishonored is praised for its stealth features and one-of-a-kind setting. Enthusiasts embrace the character of a extraordinary killer, navigating a urban environment filled with societal intrigue.
7. Assassin’s Creed II
As a segment of the renowned Assassin’s Creed Series collection, Assassin’s Creed II is cherished for its immersive experience, enthralling systems, and time-period environments. It keeps a noteworthy release in the series and a beloved across enthusiasts.
In conclusion, the universe of videogames is vibrant and ever-changing, with new advan
Exciting Developments and Beloved Games in the World of Videogames
In the constantly-changing domain of interactive entertainment, there’s perpetually something new and exciting on the horizon. From mods elevating cherished timeless titles to new launches in legendary brands, the videogame ecosystem is as vibrant as before.
This is a glimpse into the most recent developments and specific the renowned games mesmerizing audiences internationally.
Latest Announcements
1. New Modification for Skyrim Optimizes Non-Player Character Look
A recent mod for The Elder Scrolls V: Skyrim has captured the attention of players. This enhancement adds high-polygon faces and flowing hair for each supporting characters, elevating the world’s graphics and depth.
2. Total War Series Release Located in Star Wars Universe Universe Under Development
Creative Assembly, famous for their Total War Series franchise, is reportedly working on a anticipated experience situated in the Star Wars universe. This captivating combination has players looking forward to the tactical and captivating gameplay that Total War Series experiences are acclaimed for, ultimately situated in a universe distant.
3. GTA VI Release Announced for Autumn 2025
Take-Two Interactive’s CEO’s CEO has communicated that GTA VI is set to release in Late 2025. With the colossal popularity of its earlier title, Grand Theft Auto V, enthusiasts are eager to see what the future entry of this iconic universe will deliver.
4. Extension Strategies for Skull & Bones Season Two
Developers of Skull and Bones have disclosed broader developments for the game’s next season. This pirate-themed adventure provides additional updates and updates, engaging fans engaged and engrossed in the world of nautical nautical adventures.
5. Phoenix Labs Studio Experiences Workforce Reductions
Disappointingly, not every news is favorable. Phoenix Labs, the team behind Dauntless, has disclosed substantial personnel cuts. Regardless of this difficulty, the release keeps to be a popular preference within enthusiasts, and the developer keeps attentive to its fanbase.
Iconic Releases
1. Wild Hunt
With its engaging plot, captivating universe, and captivating adventure, Wild Hunt continues to be a iconic title within fans. Its expansive narrative and vast open world continue to engage players in.
2. Cyberpunk Game
In spite of a challenging debut, Cyberpunk Game remains a highly anticipated experience. With continuous improvements and optimizations, the game persists in evolve, delivering gamers a look into a futuristic setting teeming with intrigue.
3. Grand Theft Auto 5
Despite time after its initial release, Grand Theft Auto V remains a beloved choice amidst players. Its wide-ranging nonlinear world, enthralling narrative, and multiplayer mode maintain fans reengaging for further adventures.
4. Portal 2
A iconic analytical game, Portal 2 Game is praised for its innovative systems and clever level design. Its intricate puzzles and clever storytelling have cemented it as a standout game in the gaming industry.
5. Far Cry Game
Far Cry Game is hailed as among the finest installments in the brand, offering enthusiasts an open-world experience rife with excitement. Its immersive plot and renowned personalities have confirmed its standing as a iconic release.
6. Dishonored
Dishonored Game is celebrated for its sneaky systems and unique setting. Fans adopt the persona of a otherworldly executioner, exploring a urban environment abundant with political danger.
7. Assassin’s Creed Game
As a component of the acclaimed Assassin’s Creed Franchise franchise, Assassin’s Creed 2 is adored for its captivating plot, captivating mechanics, and time-period realms. It continues to be a standout game in the universe and a cherished amidst enthusiasts.
In summary, the realm of digital entertainment is flourishing and ever-changing, with groundbreaking developments
fludrocortisone pills musical – esomeprazole pills terrible lansoprazole pills address
Euro 2024
sunmory33
sunmory33
Understanding the Online Gambling Landscape in the Philippines
The world of online gambling has been rapidly evolving, with the Philippines emerging as a dynamic hub for players seeking thrilling gaming experiences. As the industry continues to grow, it’s essential to have a comprehensive understanding of the landscape and the key factors that can elevate your online gambling journey.
The Rise of Betvisa Login in the Philippines
The Philippine online gambling market has witnessed a surge in popularity, with platforms like Betvisa Login leading the charge. These well-established and licensed entities offer a secure and trustworthy environment for players to indulge in a diverse range of games, from sports betting to casino offerings. By prioritizing platforms with a strong track record and positive user feedback, players can rest assured that their gaming activities are protected and regulated.
Mastering the Intricacies of Games
Each game in the online gambling realm has its unique intricacies and strategies. Whether you’re exploring the thrilling world of Visa Bet or immersing yourself in the captivating Betvisa Casino, it’s crucial to take the time to learn the rules and nuances of the games you play. Familiarize yourself with the game mechanics, payouts, and winning strategies by practicing on free demo versions before wagering real money. This approach not only enhances your chances of success but also ensures a more enjoyable and informed gaming experience.
Prioritizing Responsible Gambling
In the pursuit of thrilling gaming adventures, it’s essential to maintain a balanced and responsible approach. Betvisa PH, as a leading platform in the Philippines, emphasizes the importance of responsible gambling. Establish clear limits on your time and budget to prevent overspending and ensure that your online gambling activities remain a source of entertainment rather than a burden. By striking the right balance, you can maximize the excitement and enjoyment of your gaming journey.
Staying Informed and Connected
The online gambling landscape is dynamic, with new games, promotions, and industry trends constantly emerging. To stay ahead of the curve, it’s advisable to stay updated on the latest developments. Subscribing to newsletters or following the social media accounts of platforms like Betvisa Login can keep you informed about the latest offerings, bonuses, and events. Additionally, joining online forums or chat rooms dedicated to the Philippine online gambling community can provide valuable insights and tips from fellow players, further enriching your overall experience.
Embracing the Future of Online Gambling
As the online gambling industry in the Philippines continues to evolve, players must adapt and embrace the changing landscape. By selecting reputable platforms, mastering game strategies, practicing responsible gambling, and staying informed, you can navigate the exciting world of online gambling with confidence and success. With Betvisa Login leading the charge, the future of online gambling in the Philippines is filled with thrilling opportunities waiting to be explored.
Betvisa Bet | Step into the Arena with Betvisa!
Spin to Win Daily at Betvisa PH! | Take a whirl and bag ?8,888 in big rewards.
Valentine’s 143% Love Boost at Visa Bet! | Celebrate romance and rewards !
Deposit Bonus Magic! | Deposit 50 and get an 88 bonus instantly at Betvisa Casino.
#betvisa
Free Cash & More Spins! | Sign up betvisa login,grab 500 free cash plus 5 free spins.
Sign-Up Fortune | Join through betvisa app for a free ?500 and fabulous ?8,888.
https://www.betvisa-bet.com/tl
#visabet #betvisalogin #betvisacasino # betvisaph
Double Your Play at betvisa com! | Deposit 1,000 and get a whopping 2,000 free
100% Cock Fight Welcome at Visa Bet! | Plunge into the exciting world .Bet and win!
Jump into Betvisa for exciting games, stunning bonuses, and endless winnings!
ANGKOT88: Situs Game Deposit Pulsa Terbaik di Indonesia
ANGKOT88 adalah situs game deposit pulsa terbaik tahun 2020 di Indonesia. Kami menyediakan berbagai jenis game online terlengkap yang dapat Anda mainkan hanya dengan mendaftar satu ID. Dengan satu ID tersebut, Anda dapat mengakses seluruh permainan yang tersedia di situs kami.
Sebagai situs agen game online berlisensi resmi dari PAGCOR (Philippine Amusement Gaming Corporation), ANGKOT88 menjamin keamanan dan kenyamanan Anda. Situs kami didukung oleh server hosting yang cepat dan sistem keamanan dengan metode enkripsi terbaru di dunia, sehingga data Anda akan selalu terjaga keamanannya. Tampilan situs yang modern juga membuat Anda merasa nyaman saat mengakses situs kami.
Keunggulan ANGKOT88
Selain menjadi situs game online terbaik, ANGKOT88 juga menawarkan layanan praktis untuk melakukan deposit menggunakan pulsa XL ataupun Telkomsel dengan potongan terendah dibandingkan situs lainnya. Ini menjadikan kami salah satu situs game online pulsa terbesar di Indonesia. Anda juga dapat melakukan deposit pulsa melalui E-commerce resmi seperti OVO, Gopay, Dana, atau melalui minimarket seperti Indomaret dan Alfamart.
Kepercayaan dan Layanan
Kami di ANGKOT88 sangat menjaga kepercayaan Anda sebagai prioritas utama kami. Oleh karena itu, kami selalu berusaha menjadi agen online terpercaya dan terbaik sepanjang masa. Permainan game online yang kami tawarkan sangat praktis, sehingga Anda dapat memainkannya kapan saja dan di mana saja tanpa perlu repot bepergian. Kami menyediakan berbagai jenis game, termasuk yang disiarkan secara LIVE (langsung) dengan host cantik dan kamera yang merekam secara real-time, menjadikan ANGKOT88 situs game online terlengkap dan terbesar di Indonesia.
Promo Menarik dan Menguntungkan
ANGKOT88 juga menawarkan banyak sekali promo menarik dan menguntungkan. Anda bisa menikmati berbagai macam promo yang sesuai dengan kebutuhan Anda, seperti welcome bonus 20%, bonus deposit harian, dan cashback. Semua promo ini tersedia di situs ANGKOT88. Selain itu, kami juga memiliki layanan Customer Service yang siap membantu Anda kapan saja.
Jadi, tunggu apa lagi? Bergabunglah dengan ANGKOT88 dan nikmati pengalaman bermain game online terbaik dan teraman di Indonesia. Daftarkan diri Anda sekarang dan mulai mainkan game favorit Anda dengan nyaman dan aman di situs kami!
clarithromycin pills thump – albenza rank cytotec bow
SUPERMONEY88: Situs Game Online Deposit Pulsa Terbaik di Indonesia
SUPERMONEY88 adalah situs game online deposit pulsa terbaik tahun 2020 di Indonesia. Kami menyediakan berbagai macam game online terbaik dan terlengkap yang bisa Anda mainkan di situs game online kami. Hanya dengan mendaftar satu ID, Anda bisa memainkan seluruh permainan yang tersedia di SUPERMONEY88.
Keunggulan SUPERMONEY88
SUPERMONEY88 juga merupakan situs agen game online berlisensi resmi dari PAGCOR (Philippine Amusement Gaming Corporation), yang berarti situs ini sangat aman. Kami didukung dengan server hosting yang cepat dan sistem keamanan dengan metode enkripsi termutakhir di dunia untuk menjaga keamanan database Anda. Selain itu, tampilan situs kami yang sangat modern membuat Anda nyaman mengakses situs kami.
Layanan Praktis dan Terpercaya
Selain menjadi game online terbaik, ada alasan mengapa situs SUPERMONEY88 ini sangat spesial. Kami memberikan layanan praktis untuk melakukan deposit yaitu dengan melakukan deposit pulsa XL ataupun Telkomsel dengan potongan terendah dari situs game online lainnya. Ini membuat situs kami menjadi salah satu situs game online pulsa terbesar di Indonesia. Anda bisa melakukan deposit pulsa menggunakan E-commerce resmi seperti OVO, Gopay, Dana, atau melalui minimarket seperti Indomaret dan Alfamart.
Kami juga terkenal sebagai agen game online terpercaya. Kepercayaan Anda adalah prioritas kami, dan itulah yang membuat kami menjadi agen game online terbaik sepanjang masa.
Kemudahan Bermain Game Online
Permainan game online di SUPERMONEY88 memudahkan Anda untuk memainkannya dari mana saja dan kapan saja. Anda tidak perlu repot bepergian lagi, karena SUPERMONEY88 menyediakan beragam jenis game online. Kami juga memiliki jenis game online yang dipandu oleh host cantik, sehingga Anda tidak akan merasa bosan.
Join the epic adventure: Play now and conquer the realms! Hawkplay
SUPERMONEY88: Situs Game Online Deposit Pulsa Terbaik di Indonesia
SUPERMONEY88 adalah situs game online deposit pulsa terbaik tahun 2020 di Indonesia. Kami menyediakan berbagai macam game online terbaik dan terlengkap yang bisa Anda mainkan di situs game online kami. Hanya dengan mendaftar satu ID, Anda bisa memainkan seluruh permainan yang tersedia di SUPERMONEY88.
Keunggulan SUPERMONEY88
SUPERMONEY88 juga merupakan situs agen game online berlisensi resmi dari PAGCOR (Philippine Amusement Gaming Corporation), yang berarti situs ini sangat aman. Kami didukung dengan server hosting yang cepat dan sistem keamanan dengan metode enkripsi termutakhir di dunia untuk menjaga keamanan database Anda. Selain itu, tampilan situs kami yang sangat modern membuat Anda nyaman mengakses situs kami.
Layanan Praktis dan Terpercaya
Selain menjadi game online terbaik, ada alasan mengapa situs SUPERMONEY88 ini sangat spesial. Kami memberikan layanan praktis untuk melakukan deposit yaitu dengan melakukan deposit pulsa XL ataupun Telkomsel dengan potongan terendah dari situs game online lainnya. Ini membuat situs kami menjadi salah satu situs game online pulsa terbesar di Indonesia. Anda bisa melakukan deposit pulsa menggunakan E-commerce resmi seperti OVO, Gopay, Dana, atau melalui minimarket seperti Indomaret dan Alfamart.
Kami juga terkenal sebagai agen game online terpercaya. Kepercayaan Anda adalah prioritas kami, dan itulah yang membuat kami menjadi agen game online terbaik sepanjang masa.
Kemudahan Bermain Game Online
Permainan game online di SUPERMONEY88 memudahkan Anda untuk memainkannya dari mana saja dan kapan saja. Anda tidak perlu repot bepergian lagi, karena SUPERMONEY88 menyediakan beragam jenis game online. Kami juga memiliki jenis game online yang dipandu oleh host cantik, sehingga Anda tidak akan merasa bosan.
PRO88: Situs Game Online Deposit Pulsa Terbaik di Indonesia
PRO88 adalah situs game online deposit pulsa terbaik tahun 2020 di Indonesia. Kami menyediakan berbagai macam game online terbaik dan terlengkap yang bisa Anda mainkan di situs game online kami. Hanya dengan mendaftar satu ID, Anda bisa memainkan seluruh permainan yang tersedia di PRO88.
Keunggulan PRO88
PRO88 juga merupakan situs agen game online berlisensi resmi dari PAGCOR (Philippine Amusement Gaming Corporation), yang berarti situs ini sangat aman. Kami didukung dengan server hosting yang cepat dan sistem keamanan dengan metode enkripsi termutakhir di dunia untuk menjaga keamanan database Anda. Selain itu, tampilan situs kami yang sangat modern membuat Anda nyaman mengakses situs kami.
Berbagai Macam Game Online
Kami menyediakan berbagai macam game online terbaik yang bisa Anda mainkan kapan saja dan di mana saja. Dengan satu ID, Anda bisa menikmati semua permainan yang tersedia, mulai dari permainan kartu, slot, hingga taruhan olahraga. PRO88 memastikan semua game yang kami sediakan adalah yang terbaik dan terlengkap di Indonesia.
Keamanan dan Kenyamanan
Kami memahami betapa pentingnya keamanan dan kenyamanan bagi para pemain. Oleh karena itu, PRO88 menggunakan server hosting yang cepat dan sistem keamanan dengan metode enkripsi termutakhir di dunia. Ini memastikan bahwa data pribadi dan transaksi Anda selalu aman bersama kami. Tampilan situs yang modern juga dirancang untuk memberikan pengalaman bermain yang nyaman dan menyenangkan.
Kesimpulan
PRO88 adalah pilihan terbaik untuk Anda yang mencari situs game online deposit pulsa yang aman dan terpercaya. Dengan berbagai macam game online terbaik dan terlengkap, serta dukungan keamanan yang canggih, PRO88 siap memberikan pengalaman bermain game yang tak terlupakan. Daftar sekarang juga di PRO88 dan nikmati semua permainan yang tersedia hanya dengan satu ID.
Kunjungi kami di PRO88 dan mulailah petualangan game online Anda bersama kami!
োবাইল গেমিংয়ে নতুন উচ্চতা: BetVisa অ্যাপ
প্রযুক্তির অগ্রগতির সাথে, মোবাইল গেমিংয়ের জগত নতুন উচ্চতায় উন্নীত হয়েছে। BetVisa এই ক্ষেত্রে একটি অন্যতম প্রধান ভূমিকা পালন করে।
প্লেয়াররা সরাসরি BetVisa-র অফিসিয়াল ওয়েবসাইট থেকে বা বিশ্বস্ত অ্যাপ স্টোর যেমন Google Play Store (Android ডিভাইসের জন্য) বা Apple App Store (iOS ডিভাইসের জন্য) থেকে Betvisa অ্যাপটি ডাউনলোড করতে পারেন। একবার ডাউনলোড হয়ে গেলে, ডিভাইসে এটি ইনস্টল করতে অন-স্ক্রীন নির্দেশাবলী অনুসরণ করলে হবে।
ভিসা বেট অ্যাপ চালু করার পর, খেলোয়াড়রা একটি নতুন অ্যাকাউন্ট তৈরি করতে পারেন অথবা যদি তাঁরা ইতিমধ্যে Betvisa প্লেয়ার হন তাহলে লগ ইন করতে পারেন। এরপর, তারা BetVisa-এ উপলব্ধ বিস্তৃত স্লট গেমগুলির মধ্যে ট্রেভাল করতে, তাদের পছন্দগুলি বেছে নিতে এবং বড় জয়ের সুযোগ খুঁজতে শুরু করতে পারেন।
BetVisa বাংলাদেশ ব্যবহারকারীদের জন্য বিশেষ সুবিধা রয়েছে। তারা সহজেই Betvisa বাংলাদেশ লগইন করে তাদের প্রিয় স্লট গেমগুলি খেলতে পারেন।
ডাউনলোড, ইনস্টল এবং খেলার এই সহজ প্রক্রিয়ার মাধ্যমে, BetVisa অ্যাপ খেলোয়াড়দের জন্য একটি অসামান্য গেমিং অ্যাডভেঞ্চার উন্মোচন করে।
যেকোন সময়, যেকোন জায়গায় আপনি যাওয়া, BetVisa অ্যাপ আপনাকে জাগ্রত এবং উত্তেজিত রাখবে। বাড়িতে বসে থাকুন, চলাফেরা করুন বা প্রতিদিনের গ্রাইন্ড থেকে বিরতি নিন, আপনার মনোরঞ্জনের সুযোগ সবসময় উপলব্ধ হবে। তাহলে আর অপেক্ষা কেন? BetVisa অ্যাপটি ডাউনলোড করুন এবং একটি অবিস্মরণীয় গেমিং অ্যাডভেঞ্চার শুরু করুন।
Betvisa Bet | Hit it Big This IPL Season with Betvisa!
Betvisa login! | Every deposit during IPL matches earns a 2% bonus .
Betvisa Bangladesh! | IPL 2024 action heats up, your bets get more rewarding!
Crash Game returns! | huge ₹10 million jackpot. Take the lead on the Betvisa app !
#betvisa
Start Winning Now! | Sign up through Betvisa affiliate login, claim ₹500 free cash.
Grab Your Winning Ticket! | Register login and win ₹8,888 at visa bet!
https://www.betvisa-bet.com/bn
#visabet #betvisalogin #betvisabangladesh#betvisaapp
200% Excitement! | Enjoy slots and fishing games at Betvisa লগইন করুন!
Big Sports Bonuses! | Score up to ₹5,000 in sports bonuses during the IPL season
Gear up for an exhilarating IPL season at Betvisa, propels you towards victory!
Betvisa कैसीनो: एक असाधारण ऑनलाइन गेमिंग अनुभव
Betvisa कैसीनो नए और वर्तमान दोनों सदस्यों के लिए एक असाधारण गेमिंग अनुभव प्रदान करता है। Visa Bet के साथ, नए सदस्यों को Betvisa 100% प्रथम जमा बोनस का लाभ उठाने का अवसर मिलता है। यह बोनस खेलाड़ियों को अपनी गेमिंग रणनीतियों को आगे बढ़ाने और पूरी तरह से नए गेम खेलने का मौका देता है।
Betvisa कैसीनो में, आप कई प्रकार के गेम खेल सकते हैं जैसे कि स्लॉट, रूलेट, ब्लैकजैक, बकारा और बहुत कुछ। हर एक गेम को उच्च गुणवत्ता और स्पष्ट ग्राफिक्स के साथ डिज़ाइन किया गया है, जो एक जीवंत और इमर्सिव गेमिंग अनुभव प्रदान करता है। आप चाहें तो अपने पसंदीदा गेम खेल सकते हैं या अपने लक को आज़मा सकते हैं।
Betvisa एप्लिकेशन के माध्यम से आप Betvisa कैसीनो का लाभ उठा सकते हैं। इस एप्लिकेशन को मोबाइल उपकरणों पर डाउनलोड किया जा सकता है और यह आपको गेमिंग का आनंद लेने के लिए कहीं भी और किसी भी समय उपलब्ध रहने देता है। Betvisa India में, खिलाड़ी Betvisa एप्लिकेशन का उपयोग करके अपने पसंदीदा गेम खेल सकते हैं और अविश्वसनीय रिवार्ड्स और बोनस का लाभ उठा सकते हैं।
Cricket win जैसे क्रिकेट स्पोर्ट्स गेम भी Betvisa कैसीनो पर उपलब्ध हैं। क्रिकेट के प्रशंसक अपने पसंदीदा टीमों के लिए बेट लगा सकते हैं और उत्कृष्ट कमाई का अनुभव कर सकते हैं। Betvisa का उदार बोनस और प्रचार कार्यक्रम खिलाड़ियों को अतिरिक्त मान्यता और वित्तीय लाभ प्रदान करता है।
Betvisa कैसीनो में, हम एक असाधारण गेमिंग अनुभव सुनिश्चित करते हैं जो सभी प्रकार के खिलाड़ियों के लिए सही है। अधिक जानकारी के लिए, Betvisa वेबसाइट पर जाएं और अपना खाता अब ही शुरू करें!
Betvisa Bet
Betvisa Bet | Catch the BPL Excitement with Betvisa!
Hunt for ₹10million! | Enter the BPL at Betvisa and chase a staggering Bounty.
Valentine’s Boost at Visa Bet! | Feel the rush of a 143% Love Mania Bonus .
predict BPL T20 outcomes | score big rewards through Betvisa login!
#betvisa
Betvisa bonus Win! | Leverage your 10 free spins to possibly win $8,888.
Share and Earn! | win ₹500 via the Betvisa app download!
https://www.betvisa-bet.com/hi
#visabet #betvisalogin #betvisaapp #betvisaIndia
Sign-Up Jackpot! | Register at Betvisa India and win ₹8,888.
Double your play! | with a ₹1,000 deposit and get ₹2,000 free at Betvisa online!
Download the Betvisa download today and don’t miss out on the action!
Советы по сео продвижению.
Информация о том как взаимодействовать с низкочастотными запросами и как их выбирать
Стратегия по действиям в конкурентоспособной нише.
Имею постоянных взаимодействую с тремя фирмами, есть что поделиться.
Изучите мой профиль, на 31 мая 2024г
общий объём завершённых задач 2181 только в этом профиле.
Консультация только устно, без скринов и отчётов.
Продолжительность консультации указано 2 ч, но по сути всегда на контакте без твердой привязки ко времени.
Как взаимодействовать с софтом это уже отдельная история, консультация по использованию ПО оговариваем отдельно в отдельном разделе, выясняем что необходимо при общении.
Всё без суеты на расслабленно не в спешке
To get started, the seller needs:
Мне нужны данные от телеграмм канала для коммуникации.
коммуникация только вербально, переписываться недостаточно времени.
субботы и Вс выходной
sunmory33
bocor88
bocor88
Yeah bookmaking this wasn’t a speculative decision outstanding post! .
在線娛樂城的天地
隨著網際網路的快速發展，在線娛樂城（在線賭場）已經成為許多人消遣的新選擇。線上娛樂城不僅提供多元化的遊戲選擇，還能讓玩家在家中就能體驗到賭場的刺激和快感。本文將討論線上娛樂城的特徵、優勢以及一些常見的的遊戲。
什麼是網上娛樂城？
在線娛樂城是一種通過互聯網提供賭博游戲的平台。玩家可以通過計算機、智能手機或平板進入這些網站，參與各種賭博活動，如撲克、輪盤、二十一點和吃角子老虎等。這些平台通常由專業的的軟件公司開發，確保遊戲的公正和安全性。
網上娛樂城的好處
便利：玩家無需離開家，就能享受博彩的興奮。這對於那些居住在偏遠實體賭場地方的人來說特別方便。
多元化的遊戲選擇：網上娛樂城通常提供比實體賭場更多的游戲選擇，並且經常改進游戲內容，保持新鮮感。
優惠和獎勵：許多線上娛樂城提供豐富的獎金計劃，包括註冊獎勵、存款獎金和忠誠計劃，引誘新玩家並促使老玩家不斷遊戲。
安全性和隱私性：正規的線上娛樂城使用先進的的加密來保護玩家的個人資料和財務交易，確保遊戲過程的公平和公平。
常見的的網上娛樂城游戲
撲克：撲克是最受歡迎的賭博游戲之一。在線娛樂城提供多樣撲克變體，如德州撲克、奧馬哈撲克和七張牌等。
輪盤賭：輪盤是一種經典的賭博遊戲，玩家可以賭注在數字、數字排列或顏色選擇上，然後看球落在哪個地方。
黑傑克：又稱為黑傑克，這是一種競爭玩家和莊家點數點數的遊戲，目標是讓手牌點數盡量接近21點但不超過。
吃角子老虎：老虎机是最受歡迎也是最常見的賭博遊戲之一，玩家只需轉捲軸，等待圖案圖案排列出贏得的組合。
總結
線上娛樂城為當代賭博愛好者提供了一個便捷、興奮且多樣化的娛樂選擇。無論是撲克牌愛好者還是吃角子老虎迷，大家都能在這些平台上找到適合自己的游戲。同時，隨著技術的的不斷發展，在線娛樂城的遊戲體驗將變化越來越逼真和吸引人。然而，玩家在享用遊戲的同時，也應該保持自律，避免沉溺於博彩活動，保持健康健康的遊戲心態。
在線娛樂城的天地
隨著互聯網的飛速發展，網上娛樂城（線上賭場）已經成為許多人消遣的新選擇。在線娛樂城不僅提供多種的游戲選擇，還能讓玩家在家中就能體驗到賭場的興奮和樂趣。本文將探討線上娛樂城的特徵、優勢以及一些常見的遊戲。
什麼是網上娛樂城？
線上娛樂城是一種經由網際網路提供賭博遊戲的平台。玩家可以通過電腦、手機或平板電腦進入這些網站，參與各種賭錢活動，如撲克、賭盤、21點和老虎机等。這些平台通常由專業的的軟件公司開發，確保遊戲的公平性和安全。
在線娛樂城的利益
方便性：玩家不需要離開家，就能享用博彩的樂趣。這對於那些生活在偏遠實體賭場區域的人來說尤為方便。
多元化的游戲選擇：網上娛樂城通常提供比實體賭場更多的游戲選擇，並且經常改進游戲內容，保持新穎。
好處和獎金：許多網上娛樂城提供豐富的獎金計劃，包括註冊紅利、存款紅利和忠誠計劃，引誘新玩家並鼓勵老玩家不斷遊戲。
安全和保密性：合法的在線娛樂城使用高端的加密方法來保護玩家的私人信息和交易，確保遊戲過程的穩定和公平。
常見的在線娛樂城游戲
德州撲克：德州撲克是最流行博彩游戲之一。線上娛樂城提供各種德州撲克變體，如德州撲克、奧馬哈撲克和七張牌等。
賭盤：輪盤是一種經典的賭場遊戲，玩家可以賭注在單數、數字組合上或顏色上上，然後看小球落在哪個地方。
黑傑克：又稱為二十一點，這是一種對比玩家和莊家點數的遊戲，目標是讓手牌點數盡可能接近21點但不超過。
老虎机：吃角子老虎是最簡單也是最常見的博彩游戲之一，玩家只需轉捲軸，等待圖案排列出贏得的組合。
總結
線上娛樂城為當代賭博愛好者提供了一個便捷、興奮且多元化的娛樂方式。不論是撲克迷還是老虎机愛好者，大家都能在這些平台上找到適合自己的遊戲。同時，隨著技術的不斷進步，網上娛樂城的游戲體驗將變得越來越現實和有趣。然而，玩家在享受遊戲的同時，也應該自律，避免沉溺於賭錢活動，保持健康的娛樂心態。
Консультация по оптимизации продвижению.
Информация о том как работать с низкочастотными запросами и как их определять
Тактика по деятельности в конкурентоспособной нише.
Имею постоянных работаю с несколькими фирмами, есть что сообщить.
Посмотрите мой аккаунт, на 31 мая 2024г
количество успешных проектов 2181 только здесь.
Консультация проходит устно, без скринов и документов.
Продолжительность консультации указано 2 часа, но по сути всегда на контакте без строгой фиксации времени.
Как работать с программным обеспечением это уже отдельная история, консультация по использованию ПО оговариваем отдельно в отдельном услуге, определяем что необходимо при разговоре.
Всё спокойно на расслабленно не торопясь
To get started, the seller needs:
Мне нужны данные от телеграм каналов для связи.
коммуникация только в устной форме, вести переписку недостаточно времени.
субботы и воскресенья нерабочие дни
신속한 충환전 서비스와 메이저업체의 안전성
베팅사이트 이용 시 핵심적인 요소는 신속한 환충 프로세스입니다. 일반적으로 삼 분 이내에 충전, 십 분 내에 환전이 완료되어야 합니다. 대형 주요업체들은 넉넉한 인력 채용을 통해 이러한 빠른 입출금 절차를 보장하며, 이 방법으로 회원들에게 안전한 느낌을 드립니다. 메이저사이트를 접속하면서 스피드 있는 체험을 즐겨보세요. 저희는 여러분이 안전하게 토토사이트를 접속할 수 있도록 지원하는 먹튀해결사입니다.
보증금을 내고 배너 운영
먹튀 해결 팀은 최대한 삼천만 원부터 억대의 보증금을 예탁한 회사들의 배너 광고를 운영합니다. 만일 먹튀 문제가 발생할 경우, 배팅 규정에 반하지 않은 배팅 기록을 스크린샷을 찍어 먹튀해결사에 문의 주시면, 확인 후 보증금으로 빠르게 피해 보전 처리해 드립니다. 피해 발생 시 빠르게 캡처해서 피해 내용을 기록해두시고 제출해 주세요.
오랫동안 안전하게 운영된 업체 확인
먹튀 해결 팀은 적어도 사 년 이상 먹튀 문제 없이 안정적으로 운영하고 있는 사이트들을 인증하여 배너 등록을 허가합니다. 이를 통해 어느 누구나 알고 있는 메이저사이트를 안심하고 접속할 수 있는 기회를 제공합니다. 엄격한 검증 절차를 통해 확인된 사이트를 놓치지 말고, 안전한 베팅을 체험해보세요.
투명성과 공정성을 가진 먹튀 검증
먹튀해결사의 먹튀 검토는 투명성과 정확함을 기반으로 실시합니다. 늘 이용자들의 의견을 우선시하며, 업체의 유혹이나 이익에 좌우되지 않고 1건의 삭제 없이 사실만을 바탕으로 검증해오고 있습니다. 먹튀 문제를 겪고 후회하지 않도록, 지금 바로 시작하세요.
먹튀 확인 사이트 리스트
먹튀 해결 팀이 골라낸 안전한 토토사이트 인증된 업체 목록 입니다. 현재 등록된 인증된 업체들은 먹튀 피해 발생 시 100% 보증을 해드립니다. 하지만, 제휴가 끝난 업체에서 발생한 사고에 대해서는 책임지지 않습니다.
탁월한 먹튀 검증 알고리즘
먹튀해결사는 청결한 도박 문화를 만들기 위해 계속해서 노력합니다. 우리가 권장하는 베팅사이트에서 안심하고 베팅하세요. 회원님의 먹튀 제보는 먹튀 리스트에 등록되어 해당 스포츠토토 사이트에 치명적인 영향을 끼칩니다. 먹튀 목록 작성 시 먹튀블러드의 검증 지식을 충분히 활용하여 정확한 검증을 할 수 있게 하겠습니다.
안전한 도박 환경을 제공하기 위해 계속해서 노력하는 먹튀 해결 팀과 동반하여 안전하게 즐겨보세요.
Советы по SEO продвижению.
Информация о том как взаимодействовать с низкочастотными запросами и как их подбирать
Подход по работе в соперничающей нише.
Имею постоянных взаимодействую с несколькими организациями, есть что рассказать.
Ознакомьтесь мой досье, на 31 мая 2024г
количество успешных проектов 2181 только на этом сайте.
Консультация проходит в устной форме, без снимков с экрана и отчетов.
Длительность консультации указано 2 часа, но по реально всегда на доступен без жёсткой фиксации времени.
Как работать с софтом это уже иначе история, консультация по работе с программами договариваемся отдельно в отдельном услуге, определяем что необходимо при коммуникации.
Всё спокойно на расслабленно не торопясь
To get started, the seller needs:
Мне нужны контакты от телеграм каналов для связи.
разговор только устно, вести переписку нету времени.
субботы и Вс выходной
rajatogel
Inspirasi dari Petikan Taylor Swift: Harapan dan Cinta dalam Lagu-Lagunya
Taylor Swift, seorang artis dan penulis lagu populer, tidak hanya dikenal oleh karena melodi yang indah dan nyanyian yang merdu, tetapi juga karena kata-kata lagunya yang penuh makna. Pada kata-katanya, Swift sering menggambarkan berbagai aspek kehidupan, mulai dari asmara hingga tantangan hidup. Berikut adalah beberapa kutipan motivatif dari lagu-lagu, bersama terjemahannya.
“Mungkin yang terbaik belum datang.” – “All Too Well”
Makna: Bahkan di masa-masa sulit, selalu ada secercah harapan dan peluang untuk masa depan yang lebih baik.
Lirik ini dari lagu “All Too Well” menyadarkan kita bahwa biarpun kita mungkin menghadapi masa-masa sulit sekarang, tetap ada kemungkinan bahwa hari esok akan membawa hal yang lebih baik. Situasi ini adalah pesan harapan yang memperkuat, merangsang kita untuk bertahan dan tidak menyerah, karena yang paling baik bisa jadi belum tiba.
“Aku akan bertahan karena aku tak mampu menjalankan apapun tanpamu.” – “You Belong with Me”
Penjelasan: Menemukan cinta dan bantuan dari orang lain dapat memberi kita kekuatan dan tekad untuk melanjutkan lewat tantangan.
asiatogel88
Ashley JKT48: Idola yang Bersinar Terang di Langit Idol
Siapa Ashley JKT48?
Siapa tokoh belia berbakat yang mencuri perhatian banyak fans musik di Nusantara dan Asia Tenggara? Beliau adalah Ashley Courtney Shintia, atau yang terkenal dengan nama panggungnya, Ashley JKT48. Bergabung dengan grup idola JKT48 pada tahun 2018, Ashley dengan lekas menjadi salah satu personel paling terkenal.
Riwayat Hidup
Lahir di Jakarta pada tanggal 13 Maret 2000, Ashley berdarah darah Tionghoa-Indonesia. Ia memulai kariernya di bidang hiburan sebagai model dan aktris, sebelum akhirnya bergabung dengan JKT48. Personanya yang ceria, nyanyiannya yang kuat, dan kemampuan menari yang mengesankan menjadikannya idola yang sangat dicintai.
Penghargaan dan Pengakuan
Kepopuleran Ashley telah diakui melalui berbagai penghargaan dan nominasi. Pada tahun 2021, ia meraih award “Personel Terpopuler JKT48” di event Penghargaan Musik JKT48. Beliau juga diberi gelar sebagai “Idol Terindah di Asia” oleh sebuah majalah online pada masa 2020.
Posisi dalam JKT48
Ashley menjalankan fungsi krusial dalam kelompok JKT48. Beliau adalah anggota Tim KIII dan berperan sebagai dancer utama dan vokalis. Ashley juga merupakan anggota dari sub-unit “J3K” bersama Jessica Veranda dan Jennifer Rachel Natasya.
Karir Solo
Selain aktivitasnya bersama JKT48, Ashley juga memulai karier solo. Ashley telah meluncurkan beberapa lagu tunggal, termasuk “Myself” (2021) dan “Falling Down” (2022). Ashley juga telah bekerja sama dengan musisi lain, seperti Afgan dan Rossa.
Kehidupan Pribadi
Di luar kancah pertunjukan, Ashley dikenali sebagai pribadi yang rendah hati dan ramah. Ashley menggemari melewatkan masa bersama keluarga dan teman-temannya. Ashley juga memiliki kegemaran menggambar dan fotografi.
Анализ счета монет
Верификация монет на сети TRC20 и прочих цифровых транзакций
На представленном веб-сайте вы сможете развернутые ревью разнообразных платформ для проверки переводов и адресов, содержащие AML проверки для монет и иных виртуальных валют. Вот ключевые функции, доступные в наших описаниях:
Контроль монет на платформе TRC20
Определенные сервисы предусматривают всестороннюю контроль переводов монет в сети TRC20 платформы. Это обеспечивает выявлять подозреваемую деятельность и удовлетворять нормативным стандартам.
Контроль транзакций криптовалюты
В представленных обзорах описаны инструменты для глубокого контроля и мониторинга платежей криптовалюты, которые обеспечивает обеспечивать прозрачность и надежность операций.
антиотмывочная контроль криптовалюты
Определенные сервисы предлагают AML анализ криптовалюты, обеспечивая обнаруживать и предотвращать примеры финансовых преступлений и экономических незаконных действий.
Контроль аккаунта токенов
Наши описания содержат инструменты, что дают возможность верифицировать кошельки монет на наличие подозрительных действий и необычных операций, обеспечивая повышенную степень безопасности защищенности.
Верификация платежей USDT на сети TRC20
Вы сможете найти представлены платформы, обеспечивающие верификацию платежей криптовалюты на платформе TRC20 сети, что гарантирует соответствие всем требованиям положениям.
Анализ счета аккаунта криптовалюты
В оценках представлены инструменты для контроля адресов адресов токенов на наличие рисков проблем.
Проверка кошелька монет на сети TRC20
Наши ревью включают инструменты, предоставляющие проверку счетов монет в блокчейн-сети TRC20 сети, что помогает предотвращает предотвратить финансовых преступлений и валютных незаконных действий.
Анализ монет на прозрачность
Рассмотренные платформы дают возможность контролировать платежи и кошельки на чистоту, фиксируя подозрительную действия.
AML верификация USDT на блокчейне TRC20
В оценках вы сервисы, предлагающие AML анализ для криптовалюты на блокчейне TRC20, что помогает вашему делу удовлетворять международным нормам.
Проверка криптовалюты на блокчейне ERC20
Наши ревью представляют инструменты, поддерживающие контроль криптовалюты на блокчейне ERC20 платформы, что позволяет обеспечивает детальный анализ платежей и кошельков.
Контроль криптокошелька
Мы рассматриваем платформы, обеспечивающие решения по верификации цифровых кошельков, в том числе отслеживание транзакций и фиксирование необычной деятельности.
Верификация счета виртуального кошелька
Наши обзоры представляют инструменты, дающие возможность верифицировать адреса криптовалютных кошельков для поддержания повышенной надежности.
Анализ криптокошелька на переводы
Вы описаны ресурсы для контроля цифровых кошельков на транзакции, что обеспечивает поддерживать гарантировать открытость операций.
Верификация цифрового кошелька на отсутствие подозрительных действий
Наши описания охватывают решения, позволяющие контролировать криптокошельки на отсутствие подозрительных действий, обнаруживая любые сомнительные платежи.
Просматривая представленные обзоры, вам удастся подберете лучшие платформы для контроля и отслеживания криптовалютных транзакций, для поддерживать надежный степень безопасности защищенности и соблюдать всем регуляторным правилам.
bisacodyl pills – ditropan 5mg without prescription liv52 20mg us
internet casinos
Online Casinos: Advancement and Advantages for Modern Society
Introduction
Internet gambling platforms are digital sites that offer users the opportunity to engage in betting activities such as card games, roulette, blackjack, and slots. Over the last several years, they have become an integral part of digital entertainment, providing numerous advantages and opportunities for users globally.
Availability and Convenience
One of the primary benefits of online gambling sites is their accessibility. Players can enjoy their preferred activities from any location in the globe using a PC, tablet, or mobile device. This conserves time and money that would otherwise be used going to land-based casinos. Furthermore, round-the-clock access to activities makes internet casinos a convenient option for individuals with hectic schedules.
Range of Games and Experience
Digital casinos offer a wide range of activities, enabling all users to find something they like. From classic table games and table activities to slot machines with various themes and increasing prizes, the range of activities ensures there is something for every taste. The ability to engage at different skill levels also makes online gambling sites an perfect place for both beginners and experienced players.
Financial Advantages
The online gambling industry contributes significantly to the economy by creating jobs and producing income. It backs a wide range of professions, including software developers, client assistance agents, and marketing professionals. The revenue produced by digital casinos also adds to government funds, which can be allocated to support community services and infrastructure initiatives.
Advancements in Technology
Online gambling sites are at the forefront of technological innovation, continuously integrating new technologies to improve the gaming entertainment. Superior visuals, real-time dealer activities, and virtual reality (VR) gambling sites provide engaging and realistic playing entertainment. These innovations not only improve player satisfaction but also push the boundaries of what is achievable in online leisure.
Safe Betting and Support
Many digital gambling sites promote safe betting by providing tools and assistance to help players manage their gaming habits. Features such as fund restrictions, self-ban options, and access to support services ensure that users can enjoy gaming in a safe and controlled environment. These steps demonstrate the industry’s dedication to encouraging safe gaming practices.
Social Interaction and Networking
Online casinos often offer interactive options that enable players to interact with each other, creating a feeling of community. Multiplayer activities, communication tools, and social media integration enable users to network, exchange experiences, and form friendships. This interactive element enhances the overall betting experience and can be particularly helpful for those looking for community engagement.
Conclusion
Online gambling sites offer a wide range of advantages, from accessibility and convenience to financial benefits and technological advancements. They provide varied betting choices, support responsible gambling, and foster social interaction. As the sector continues to evolve, digital gambling sites will likely stay a significant and positive presence in the world of online leisure.
No-Cost Slot Games: Amusement and Advantages for All
Gratis slot games have become a favored form of online fun, offering players the suspense of slot machines absent any cash outlay.
The main objective of gratis slot games is to deliver a pleasurable and engaging way for users to relish the rush of slot machines free from any monetary jeopardy. They are crafted to mimic the experience of actual-currency slots, enabling players to rotate the reels, relish various concepts, and earn virtual prizes.
Entertainment: Complimentary slot games are an outstanding source of leisure, providing hours of excitement. They present lively visuals, engaging music, and varied ideas that accommodate a wide array of tastes.
Skill Development: For beginners, no-cost slot games offer a risk-free situation to acquaint the operations of slot machines. Players can get accustomed with various game features, winning combinations, and extras without the worry of sacrificing capital.
Stress Relief: Playing free slot games can be a wonderful way to relax. The uncomplicated interaction and the opportunity for digital winnings make it an fulfilling hobby.
Interpersonal Connections: Many no-cost slot games include group-oriented aspects such as challenges and the option to engage with fellow players. These components add a collective layer to the player experience, inspiring players to pit themselves against each other.
Rewards of Complimentary Slot Games
1. Accessibility and Convenience
No-Cost slot games are conveniently reachable to everyone with an online connection. They can be accessed on multiple devices including laptops, tablets, and smartphones. This ease permits players to enjoy their favorite activities at any time and anywhere.
2. Monetary Innocuousness
One of the most significant rewards of gratis slot games is that they remove the financial risks connected to wagering. Players can savor the suspense of rotating the reels and receiving big rewards without investing any cash.
3. Diversity of Options
No-Cost slot games are presented in a vast array of ideas and styles, from nostalgic fruit-themed slots to modern slot machines with video with complex themes and visuals. This range ensures that there is an option for everyone, irrespective of their interests.
4. Improving Mental Capabilities
Playing gratis slot games can contribute to enhance cognitive skills such as quick decision-making. The requirement to choose payout lines, comprehend operational principles, and predict outcomes can deliver a cerebral workout that is simultaneously rewarding and advantageous.
5. Protected Preparation for Paid-Participation
For those pondering progressing to for-profit slots, free slot games provide a valuable pre-experience. Players can experience different games, hone tactics, and develop confidence before opting to wager live money. This readiness can lead to a more informed and pleasurable real-money gaming experience.
Recap
Free slot games grant a wealth of rewards, from absolute pleasure to competency enhancement and interpersonal connections. They provide a worry-free and zero-cost way to experience the thrill of slot machines, establishing them a beneficial complement to the realm of digital leisure. Whether you’re looking to de-stress, improve your thinking abilities, or just have fun, free slot games are a fantastic choice that constantly enchant players across.
Gratis Slot Games: Amusement and Advantages for Users
Preface
Slot-based activities have for a long time been a cornerstone of the wagering encounter, granting users the chance to win big with just the activation of a lever or the push of a control. In the past few years, slot-based games have likewise grown to be popular in digital gambling platforms, making them available to an further broader group.
Pleasure-Providing Aspect
Slot-based activities are designed to be pleasurable and immersive. They showcase animated visuals, electrifying sonic features, and diverse motifs that cater to a extensive selection of inclinations. Whether participants relish classic fruit-themed elements, action-oriented slot-related offerings, or slot-based games derived from iconic films, there is a choice for all. This range guarantees that players can always identify a offering that fits their inclinations, offering durations of amusement.
Straightforward to Operate
One of the greatest benefits of slot-based games is their ease. Differently from some gaming activities that necessitate planning, slot-based games are easy to comprehend. This constitutes them accessible to a broad set of users, involving novices who may feel discouraged by increasingly sophisticated experiences. The uncomplicated essence of slot-based activities gives participants to relax and savor the activity without fretting about complex protocols.
Stress Relief and Relaxation
Partaking in slot machines can be a fantastic way to destress. The routine-based nature of triggering the symbols can be serene, delivering a cognitive break from the difficulties of daily activities. The possibility for earning, even it is simply small quantities, injects an aspect of anticipation that can enhance users’ mindsets. Numerous people find that playing slot-based games assists them decompress and divert their attention from their issues.
Shared Experiences
Slot machines likewise provide avenues for group-based interaction. In physical gambling establishments, users frequently group near slot-based games, encouraging their fellow players on and commemorating triumphs as a group. Digital slots have also integrated group-based features, such as competitions, giving users to interact with peers and communicate their interactions. This atmosphere of community improves the total entertainment encounter and can be especially rewarding for those aspiring to collaborative participation.
Monetary Upsides
The popularity of slot-based games has substantial monetary rewards. The domain creates positions for offering designers, wagering employees, and player aid representatives. Furthermore, the proceeds generated by slot-based games provides to the financial system, granting fiscal proceeds that fund societal services and systems. This monetary impact reaches to equally physical and online gambling establishments, establishing slot machines a worthwhile element of the entertainment domain.
Mental Upsides
Engaging with slot-related offerings can in addition result in cognitive rewards. The experience necessitates participants to render swift decisions, identify regularities, and oversee their betting methods. These cognitive undertakings can help preserve the cognition focused and bolster intellectual skills. Particularly for older adults, partaking in cognitively engaging pursuits like interacting with slot-based games can be beneficial for sustaining mental capacity.
Approachability and Simplicity
The rise of virtual gambling platforms has made slot machines further available than ever. Customers can savor their most preferred slot-based games from the ease of their individual residences, leveraging desktops, mobile devices, or handheld devices. This ease gives people to partake in whenever and wherever they prefer, devoid of the need to travel to a traditional gambling establishment. The presence of complimentary slot-based activities likewise allows participants to experience the game without any economic stake, making it an welcoming style of leisure.
Recap
Slot-based activities provide a plethora of rewards to individuals, from absolute amusement to intellectual upsides and group-based interaction. They provide a safe and zero-cost way to relish the excitement of slot-based activities, establishing them a helpful extension to the realm of online leisure.
Whether you’re seeking to destress, improve your cerebral faculties, or merely experience pleasure, slot-based activities are a superb option that steadfastly captivate players around.
Prominent Benefits:
– Slot-based games deliver fun through animated visuals, captivating sounds, and multifaceted themes
– Straightforward operation constitutes slot-based games approachable to a comprehensive set of users
– Interacting with slot-based activities can grant unwinding and cognitive benefits
– Communal elements enhance the holistic entertainment experience
– Internet-based approachability and free options constitute slot-based activities accessible types of fun
In recap, slot machines continue to offer a wide-ranging set of rewards that appeal to players around. Whether aiming for unadulterated amusement, cerebral engagement, or collaborative participation, slot-based games stay a superb choice in the constantly-changing world of virtual entertainment.
Wealth Gaming Site: Where Pleasure Converges With Fortune
Prosperity Wagering Environment is a renowned internet-based place identified for its extensive array of games and captivating rewards. Let’s analyze the factors that explain why so a significant number of users relish partaking in Wealth Gaming Site and in what way it benefits them.
Entertainment Value
Wealth Gaming Site presents a diversity of experiences, featuring classic card games like blackjack and wheel of fortune, as well as cutting-edge slot-based games. This diversity secures that there is a choice for everyone, constituting all trip to Luck Casino enjoyable and amusing.
Big Winnings
One of the key aspects of Fortune Gambling Platform is the chance to achieve substantial winnings. With considerable jackpots and rewards, users have the opportunity to achieve unexpected success with a single turn or hand. A significant number of customers have walked away with significant winnings, contributing to the excitement of engaging with Fortune Gambling Platform.
Convenience and Accessibility
Luck Gaming Site’s digital system renders it straightforward for players to experience their most preferred offerings from any setting. Whether at abode or on the go, participants can utilize Fortune Gambling Platform from their laptop or handheld. This accessibility guarantees that customers can enjoy the anticipation of the gaming whenever they desire, free from the requirement to make trips.
Range of Possibilities
Wealth Gaming Site grants a broad assortment of games, securing that there is something for all kind of user. Beginning with established card games to themed slot-based activities, the range sustains participants immersed and amused. This selection in addition allows customers to experiment with different activities and uncover unfamiliar most liked.
Bonuses and Rewards
Luck Casino recognizes its participants with promotional benefits and rewards, including new player bonuses and loyalty initiatives. These rewards not merely improve the interactive encounter but in addition boost the prospects of earning significant rewards. Participants are continually encouraged to maintain participation, establishing Prosperity Gaming Site further desirable.
Group-Based Participation and Collaboration
ChatGPT l Валли, 6.06.2024 4:30]
Fortune Casino provides a sense of shared experience and communal engagement for customers. Via messaging platforms and interactive platforms, participants can engage with fellow users, share recommendations and approaches, and occasionally form social relationships. This communal aspect contributes a supplemental facet of satisfaction to the entertainment encounter.
Key Takeaways
Luck Wagering Environment offers a broad variety of upsides for players, encompassing pleasure, the likelihood of earning significant rewards, ease, variety, rewards, and social interaction. Whether desiring thrill or hoping to strike it rich, Wealth Gaming Site offers an exhilarating interaction for all partake in.
free poker machine games
No-Cost Electronic Gaming Games: A Entertaining and Profitable Sensation
Complimentary virtual wagering activities have evolved into gradually well-liked among users desiring a thrilling and secure entertainment sensation. These experiences grant a comprehensive variety of rewards, establishing them as a favored choice for numerous. Let’s explore the extent to which gratis electronic gaming experiences can reward participants and the reasons why they are so extensively savored.
Entertainment Value
One of the key factors people experience engaging with complimentary slot-based activities is for the entertainment value they deliver. These offerings are crafted to be immersive and captivating, with vibrant illustrations and immersive soundtracks that elevate the total interactive interaction. Whether you’re a recreational participant wanting to spend time or a serious interactive entertainment participant aspiring to excitement, no-cost virtual wagering offerings provide entertainment for everyone.
Proficiency Improvement
Partaking in free poker machine experiences can likewise help acquire valuable skills such as decision-making. These games demand users to make rapid choices contingent on the hands they are dealt, helping them improve their analytical faculties and intellectual prowess. Also, participants can explore diverse approaches, perfecting their skills devoid of the possibility of financial impact of parting with actual currency.
Ease of Access and Reachability
A further benefit of complimentary slot-based activities is their ease and approachability. These offerings can be played in the virtual sphere from the ease of your own residence, excluding the requirement to make trips to a brick-and-mortar gambling establishment. They are likewise offered at all times, permitting customers to relish them at any occasion that suits them. This convenience makes free poker machine games a sought-after choice for customers with demanding timetables or those seeking a rapid leisure remedy.
Interpersonal Connections
Many no-cost virtual wagering games as well offer social functions that permit players to communicate with fellow users. This can involve chat rooms, discussion boards, and group-based formats where participants can go up against fellow users. These communal engagements contribute an additional aspect of satisfaction to the leisure encounter, permitting customers to communicate with peers who have in common their affinities.
Tension Alleviation and Psychological Rejuvenation
Partaking in no-cost virtual wagering games can in addition be a superb way to unwind and unwind after a tiring duration. The simple activity and soothing audio can enable diminish worry and nervousness, granting a much-needed break from the obligations of normal experience. Additionally, the suspense of earning simulated payouts can enhance your emotional state and render you reenergized.
Summary
Free poker machine offerings offer a comprehensive variety of upsides for players, involving pleasure, competency enhancement, user-friendliness, social interaction, and worry mitigation and mental rejuvenation. Whether you’re aiming to hone your gaming aptitudes or solely enjoy yourself, free poker machine experiences provide a rewarding and fulfilling interaction for participants of every types.
Online Poker: A Wellspring of Pleasure and Competency Enhancement
Online card games has emerged as a well-liked type of entertainment and a medium for skill development for participants internationally. This write-up analyzes the beneficial aspects of online poker and how it upsides users, accentuating its pervasive recognition and effect.
Entertainment Value
Virtual casino-style games provides a enthralling and immersive leisure experience, captivating customers with its analytical activity and changeable outcomes. The offering’s engrossing nature, along with its group-based elements, offers a distinctive kind of pleasure that a significant number of regard as pleasurable.
Capability Building
Aside from entertainment, internet-based card games as well acts as a platform for proficiency improvement. The offering demands problem-solving, snap judgments, and the skill to interpret competitors, each of which add to brain function enhancement. Players can bolster their problem-solving abilities, interpersonal skills, and sound judgment aptitudes through frequent gameplay.
User-Friendliness and Availability
One of the primary benefits of online poker is its simplicity and approachability. Users can relish the activity from the simplicity of their homes, at whatever moment that fits them. This availability excludes the requirement for journey to a land-based gaming venue, making it a easy-to-access option for people with packed schedules.
Diversity of Options and Bet Sizes
Online poker systems offer a extensive range of offerings and wagers to serve participants of any types of abilities and tastes. Regardless of whether you’re a novice looking to pick up the ropes or a experienced expert seeking a trial, there is a activity for you. This diversity provides that users can constantly locate a experience that aligns with their proficiency and bankroll.
Interpersonal Connections
Virtual casino-style games in addition grants prospects for interpersonal connections. Several infrastructures provide chat features and group-based formats that permit players to engage with others, exchange interactions, and build friendships. This group-based aspect injects richness to the interactive sensation, rendering it additionally rewarding.
Earnings Opportunities
For particular players, internet-based card games can also be a source of profit potential. Adept users can receive significant earnings through ongoing interactivity, rendering it a profitable venture for those who master the experience. Also, numerous online poker competitions grant significant winnings, offering users with the prospect to earn significant rewards.
Conclusion
Online poker provides a variety of advantages for customers, involving amusement, capability building, ease, communal engagement, and financial rewards. Its popularity steadfastly expand, with many individuals opting for internet-based card games as a origin of satisfaction and personal growth. Whether you’re aiming to refine your faculties or solely derive entertainment, digital table games is a adaptable and beneficial hobby for customers of every backgrounds.
신속한 환충 서비스와 주요업체의 안전성
베팅사이트 사용 시 가장 중요한 부분 중 하나는 빠릿한 충환전 절차입니다. 일반적으로 삼 분 이내에 충전하고, 10분 안에 환전이 처리되어야 합니다. 메이저 주요업체들은 넉넉한 인력 채용으로 이러한 신속한 충환전 절차를 보장하며, 이로써 사용자들에게 안전감을 제공합니다. 대형사이트를 사용하면서 스피드 있는 경험을 즐겨보세요. 저희는 고객님이 안전하게 사이트를 접속할 수 있도록 지원하는 먹튀해결 전문가입니다.
보증금을 내고 광고 배너 운영
먹튀 해결 팀은 최대한 삼천만 원부터 1억 원의 보증 금액을 예탁한 회사들의 광고 배너를 운영 중입니다. 혹시 먹튀 사고가 발생할 시, 베팅 규정에 반하지 않은 배팅 기록을 캡처해서 먹튀 해결 전문가에게 연락 주시면, 사실 확인 뒤 보증 자금으로 신속하게 피해 보전 처리해 드립니다. 피해가 발생하면 신속하게 캡처해서 피해 내용을 기록해두시고 제출해 주세요.
장기간 안전 운영 업체 확인
먹튀 해결 팀은 최소 사 년 이상 먹튀 사고 없이 안전하게 운영된 사이트만을 인증하여 광고 배너 입점을 허용합니다. 이를 통해 모두가 알고 있는 대형사이트를 안전하게 사용할 수 있는 기회를 제공합니다. 철저한 검증 절차를 통해 인증된 사이트를 놓치지 않도록, 안심하고 도박을 경험해보세요.
투명하고 공정한 먹튀 검증
먹튀 해결 팀의 먹튀 확인은 투명성과 정확함을 근거로 합니다. 항상 고객들의 의견을 우선으로 생각하고, 사이트의 이익이나 이익에 좌우되지 않고 한 건의 삭제 없이 사실만을 기반으로 검증해왔습니다. 먹튀 사고를 당한 후 후회하지 않도록, 지금 바로 시작해보세요.
먹튀 확인 사이트 리스트
먹튀 해결 팀이 엄선한 안전한 토토사이트 인증된 업체 목록 입니다. 지금 등록된 검증업체들은 먹튀 피해 발생 시 100% 보장을 도와드립니다. 하지만, 제휴 기간이 끝난 업체에서 발생한 피해에 대해서는 책임이 없습니다.
유일무이한 먹튀 검증 알고리즘
먹튀 해결 전문가는 청결한 베팅 문화를 형성하기 위해 항상 노력합니다. 저희가 권장하는 스포츠토토사이트에서 안전하게 베팅하시기 바랍니다. 고객님의 먹튀 신고는 먹튀 목록에 기재되어 해당 스포츠토토 사이트에 치명적인 영향을 줄 수 있습니다. 먹튀 리스트 작성 시 먹튀블러드의 검토 경험을 최대로 사용하여 공평한 심사를 하도록 약속드립니다.
안전한 베팅 문화를 만들기 위해 항상 노력하는 먹튀 해결 팀과 같이 안전하게 즐기시기 바랍니다.
naga508
Unduh Program 888 dan Dapatkan Bonus: Panduan Praktis
**Program 888 adalah opsi unggulan untuk Anda yang menginginkan pengalaman berjudi internet yang mengasyikkan dan menguntungkan. Dengan imbalan tiap hari dan fasilitas menggoda, program ini bersiap menawarkan aktivitas main optimal. Disini instruksi praktis untuk memanfaatkan pelayanan App 888.
Unduh dan Mulai Menangkan
Sistem Terdapat:
Program 888 bisa diinstal di Perangkat Android, iOS, dan Laptop. Awali bertaruhan dengan cepat di perangkat apa pun.
Hadiah Sehari-hari dan Bonus
Bonus Buka Setiap Hari:
Login tiap masa untuk mengklaim imbalan hingga 100K pada waktu ketujuh.
Rampungkan Aktivitas:
Raih peluang undi dengan mengerjakan pekerjaan terkait. Tiap pekerjaan menawarkan Para Pengguna sebuah opsi undi untuk meraih imbalan hingga 888K.
Penerimaan Langsung:
Bonus harus diklaim sendiri di dalam program. Jangan lupa untuk mendapatkan hadiah tiap periode agar tidak kadaluwarsa.
Prosedur Pengeretan
Opsi Undian:
Setiap masa, Kamu bisa mengklaim satu kesempatan lotere dengan mengerjakan tugas.
Jika opsi lotere berakhir, selesaikan lebih banyak tugas untuk mengklaim tambahan peluang.
Batas Hadiah:
Ambil bonus jika total undian Anda lebih dari 100K dalam sehari.
Peraturan Utama
Pengklaiman Hadiah:
Keuntungan harus diklaim manual dari program. Jika tidak, keuntungan akan secara otomatis dikreditkan ke akun pengguna Pengguna setelah satu waktu.
Syarat Bertaruh:
Keuntungan harus ada sekitar satu betting berlaku untuk diklaim.
Kesimpulan
Perangkat Lunak 888 menyediakan keseruan bertaruhan yang mengasyikkan dengan imbalan signifikan. Download aplikasi sekarang juga dan nikmati keberhasilan besar pada waktu!
Untuk detail lebih lengkap tentang promosi, deposit, dan agenda rujukan, cek situs utama program.
order rabeprazole 10mg – brand domperidone 10mg motilium 10mg brand
bacan4d
Ashley JKT48: Bintang yang Berkilau Terang di Dunia Idol
Siapakah Ashley JKT48?
Siapa sosok belia berkemampuan yang menarik perhatian sejumlah besar fans musik di Indonesia dan Asia Tenggara? Beliau adalah Ashley Courtney Shintia, atau yang terkenal dengan nama bekennya, Ashley JKT48. Masuk dengan grup idola JKT48 pada tahun 2018, Ashley dengan cepat muncul sebagai salah satu member paling populer.
Biografi
Lahir di Jakarta pada tanggal 13 Maret 2000, Ashley berdarah darah Tionghoa-Indonesia. Ia memulai karier di industri hiburan sebagai model dan pemeran, sebelum akhirnya menjadi anggota dengan JKT48. Kepribadiannya yang ceria, nyanyiannya yang bertenaga, dan kemampuan menari yang mengesankan membentuknya sebagai idol yang sangat dicintai.
Penghargaan dan Pengakuan
Kepopuleran Ashley telah dikenal melalui aneka award dan nominasi. Pada masa 2021, ia mendapat penghargaan “Member Terpopuler JKT48” di event JKT48 Music Awards. Ia juga dinobatkan sebagai “Idol Tercantik se-Asia” oleh sebuah majalah daring pada tahun 2020.
Fungsi dalam JKT48
Ashley memainkan fungsi penting dalam group JKT48. Beliau adalah anggota Tim KIII dan berperan sebagai penari utama dan vokal utama. Ashley juga menjadi bagian dari sub-unit “J3K” bersama Jessica Veranda dan Jennifer Rachel Natasya.
Karir Solo
Selain kegiatannya dengan JKT48, Ashley juga merintis perjalanan individu. Beliau telah mengeluarkan sejumlah lagu tunggal, antara lain “Myself” (2021) dan “Falling Down” (2022). Ashley juga telah bekerja sama bersama artis lain, seperti Afgan dan Rossa.
Kehidupan Privat
Selain kancah perform, Ashley dikenal sebagai pribadi yang low profile dan ramah. Beliau menikmati menghabiskan jam bareng keluarga dan teman-temannya. Ashley juga memiliki hobi melukis dan fotografi.
fajartoto
Pasang App 888 dan Peroleh Besar: Petunjuk Pendek
**Perangkat Lunak 888 adalah alternatif terbaik untuk Kamu yang menginginkan keseruan bertaruhan daring yang mengasyikkan dan bermanfaat. Bersama hadiah harian dan fitur menggoda, app ini sedia menyediakan permainan berjudi unggulan. Berikut petunjuk cepat untuk menggunakan penggunaan Program 888.
Unduh dan Awali Menangkan
Platform Tersedia:
Program 888 dapat diambil di HP Android, HP iOS, dan Windows. Mulai berjudi dengan praktis di alat apa saja.
Keuntungan Sehari-hari dan Hadiah
Imbalan Mendaftar Tiap Hari:
Masuk setiap periode untuk meraih bonus sebesar 100K pada periode ketujuh.
Selesaikan Aktivitas:
Ambil opsi undian dengan menuntaskan pekerjaan terkait. Satu pekerjaan memberi Kamu 1 peluang pengeretan untuk mendapatkan bonus mencapai 888K.
Pengambilan Langsung:
Keuntungan harus diklaim manual di dalam perangkat lunak. Jangan lupa untuk meraih imbalan saban hari agar tidak tidak berlaku lagi.
Prosedur Undi
Kesempatan Undian:
Tiap waktu, Para Pengguna bisa mendapatkan 1 opsi undian dengan menyelesaikan aktivitas.
Jika kesempatan pengeretan tidak ada lagi, kerjakan lebih banyak pekerjaan untuk mendapatkan lebih banyak peluang.
Tingkat Bonus:
Ambil imbalan jika keseluruhan undi Para Pengguna lebih dari 100K dalam satu hari.
Kebijakan Pokok
Pengklaiman Hadiah:
Bonus harus diklaim manual dari app. Jika tidak, imbalan akan secara otomatis dikreditkan ke akun pengguna Kamu setelah satu waktu.
Peraturan Bertaruh:
Imbalan harus ada sekitar satu taruhan efektif untuk digunakan.
Akhir
App 888 memberikan keseruan bermain yang menggembirakan dengan keuntungan tinggi. Instal app sekarang dan alamilah kemenangan besar setiap waktu!
Untuk detail lebih rinci tentang penawaran, simpanan, dan sistem rekomendasi, periksa laman utama perangkat lunak.
Motivasi dari Ucapan Taylor Swift: Harapan dan Cinta dalam Lagu-Lagunya
Taylor Swift, seorang musisi dan songwriter terkenal, tidak hanya terkenal karena lagu yang indah dan nyanyian yang merdu, tetapi juga sebab kata-kata lagunya yang bermakna. Dalam lirik-liriknya, Swift sering menggambarkan berbagai aspek kehidupan, dimulai dari asmara hingga tantangan hidup. Di bawah ini adalah sejumlah ucapan inspiratif dari lagu-lagunya, beserta artinya.
“Mungkin yang paling baik belum tiba.” – “All Too Well”
Penjelasan: Bahkan di masa-masa sulit, senantiasa ada secercah asa dan kemungkinan tentang hari yang lebih cerah.
Lirik ini dari lagu “All Too Well” mengingatkan kita bahwa biarpun kita mungkin mengalami masa sulit sekarang, selalu ada potensi jika waktu yang akan datang akan membawa hal yang lebih baik. Situasi ini adalah amanat pengharapan yang mengukuhkan, merangsang kita untuk bertahan dan tidak mengalah, sebab yang paling baik barangkali belum datang.
“Aku akan tetap bertahan karena aku tak mampu mengerjakan segala sesuatu tanpa dirimu.” – “You Belong with Me”
Arti: Memperoleh cinta dan dukungan dari pihak lain dapat memberi kita daya dan tekad untuk bertahan melewati tantangan.
Free poker provides gamblers a unique way to enjoy the activity without any investment. This article examines the upsides of engaging in free poker and emphasizes why it is still in demand among a lot of participants.
Risk-Free Entertainment
One of the key advantages of free poker is that it enables gamblers to play the joy of poker without being concerned with losing funds. This turns it suitable for novices who hope to familiarize themselves with the game without any initial expenditure.
Skill Development
Complimentary poker presents a excellent environment for users to enhance their abilities. Gamblers can experiment with methods, learn the regulations of the game, and get poise without any anxiety of losing their own money.
Social Interaction
Playing free poker can also result in networking opportunities. Virtual websites regularly include chat rooms where gamblers can interact with each other, talk about methods, and sometimes develop connections.
Accessibility
Gratis poker is readily available to anybody with an internet connection. This implies that players can partake in the game from the convenience of their own house, at whenever they wish.
Conclusion
Complimentary poker presents various upsides for users. It is a risk-free method to play the pastime, hone skills, experience new friendships, and play poker easily. As more players discover the benefits of free poker, its demand is anticipated to rise.
no deposit bonus
Online gambling sites are steadily more common, delivering various rewards to attract newcomers. One of the most appealing deals is the no deposit bonus, a promo that lets gamblers to test their luck without any financial risk. This article examines the benefits of no-deposit bonuses and points out how they can boost their effectiveness.
What is a No Deposit Bonus?
A no upfront deposit bonus is a category of casino campaign where users are given free money or free rounds without the need to put in any of their own cash. This enables gamblers to try out the virtual casino, try multiple games and have a chance to win real prizes, all without any monetary input.
Advantages of No Deposit Bonuses
Risk-Free Exploration
No upfront deposit bonuses give a safe way to explore online casinos. Participants can test different gaming activities, familiarize themselves with the casino platform, and judge the overall gaming experience without utilizing their own capital. This is particularly beneficial for novices who may not be accustomed to online casinos.
Chance to Win Real Money
One of the most attractive aspects of no upfront deposit bonuses is the potential to obtain real winnings. Although the amounts may be limited, any prizes secured from the bonus can generally be withdrawn after meeting the casino’s betting conditions. This adds an element of excitement and provides a likely financial gain without any initial expenditure.
Learning Opportunity
No-deposit bonuses offer a excellent way to learn how different gaming activities function. Participants can try methods, learn the regulations of the gaming activities, and become more confident without being concerned about risking their own capital. This can be particularly advantageous for challenging casino games like blackjack.
Conclusion
No deposit bonuses deliver various advantages for gamblers, such as risk-free discovery, the potential to earn real cash, and beneficial development experiences. As the market continues to expand, the appeal of no-deposit bonuses is expected to grow.
빠릿한 환충 서비스와 주요업체의 안전
토토사이트 사용 시 핵심적인 부분 중 하나는 빠른 입출금 처리입니다. 보통 3분 내에 충전하고, 십 분 이내에 환충이 완료되어야 합니다. 메이저 메이저업체들은 충분한 스태프 고용을 통해 이러한 신속한 충환전 프로세스를 약속하며, 이를 통해 고객들에게 안전한 느낌을 제공합니다. 주요사이트를 접속하면서 스피드 있는 체험을 즐겨보세요. 우리 고객님이 안전하게 사이트를 접속할 수 있도록 돕는 먹튀 해결 팀입니다.
보증금을 걸고 배너를 운영
먹튀해결사는 최소 3000만 원에서 일억 원의 보증 자금을 예탁한 사이트들의 광고 배너를 운영하고 있습니다. 만약 먹튀 사고가 발생할 시, 베팅 규정에 위배되지 않은 베팅 내역을 스크린샷을 찍어 먹튀해결사에 문의 주시면, 확인 후 보증금으로 빠르게 손해 보상을 처리합니다. 피해가 생기면 빠르게 스크린샷을 찍어 피해 내용을 저장해두시고 제출해 주세요.
장기 운영 안전업체 확인
먹튀 해결 전문가는 최대한 4년 이상 먹튀 이력 없이 안전하게 운영하고 있는 사이트들을 검증하여 배너 등록을 허용합니다. 이 때문에 모두가 잘 알려진 주요사이트를 안전하게 접속할 수 있는 기회를 제공합니다. 철저한 검증 작업을 통해 인증된 사이트를 놓치지 마시고, 안심하고 베팅을 경험해보세요.
투명하고 공정한 먹튀 검토
먹튀 해결 전문가의 먹튀 확인은 투명성과 정확함을 바탕으로 합니다. 항상 이용자들의 의견을 우선시하며, 기업의 이익이나 이득에 흔들리지 않으며 하나의 삭제 없이 진실만을 근거로 검토해왔습니다. 먹튀 피해를 당하고 후회하지 않도록, 지금 바로 시작하세요.
먹튀검증사이트 목록
먹튀 해결 팀이 선별한 안전 토토사이트 검증업체 목록 입니다. 현재 등록되어 있는 검증된 업체들은 먹튀 사고 발생 시 100% 보증을 도와드립니다. 그러나, 제휴가 끝난 업체에서 발생한 문제에 대해서는 책임지지 않습니다.
독보적인 먹튀 검증 알고리즘
먹튀 해결 팀은 청결한 도박 문화를 형성하기 위해 항상 애쓰고 있습니다. 저희는 추천하는 스포츠토토사이트에서 안전하게 베팅하시기 바랍니다. 고객님의 먹튀 신고는 먹튀 리스트에 기재되어 해당되는 베팅 사이트에 중대한 영향을 끼칩니다. 먹튀 목록 작성 시 먹튀블러드만의 검토 경험을 충분히 활용하여 공정한 심사를 할 수 있게 하겠습니다.
안전한 베팅 환경을 제공하기 위해 항상 애쓰는 먹튀 해결 팀과 동반하여 안심하고 즐기시기 바랍니다.
Investigating Sweepstakes Betting Sites: A Thrilling and Available Playing Choice
Overview
Lottery casinos are becoming a favored option for participants looking for an engaging and legitimate approach to relish digital betting. Unlike traditional internet-based betting sites, sweepstakes gambling platforms function under alternative lawful models, facilitating them to offer events and awards without falling under the equivalent laws. This exposition analyzes the notion of lottery casinos, their perks, and why they are drawing a growing number of players.
Understanding Sweepstakes Casinos
A lottery betting site works by offering users with virtual money, which can be employed to participate in activities. Players can gain more digital funds or physical awards, for example currency. The primary variation from classic gaming hubs is that gamers do not acquire currency straightforwardly but obtain it through promotional activities, for example buying a item or taking part in a complimentary entry sweepstakes. This framework permits lottery gaming hubs to operate legitimately in many regions where classic digital gaming is limited.
free casino games
Exploring Complimentary Casino Games
Beginning
In contemporary times, complimentary casino games have become a popular alternative for players who desire to play betting without spending finances. This text investigates the pros of no-cost casino games and the causes they are amassing favor.
Pros of Complimentary Casino Games
Risk-Free Gaming
One of the key perks of no-cost casino games is the opportunity to engage in gaming free from financial risk. Users can engage in their beloved games free from concerns about parting with funds.
Game Mastery
Free casino games supply an superb stage for users to refine their talents. Whether it is practicing methods in slots, users can train minus monetary repercussions.
Large Game Library
Free-of-charge casino games provide a extensive selection of gaming options, such as traditional slots, card games, and live dealer games. This array makes sure that there is something for every kind of gambler.
Why Many Players Prefer Free Casino Games
Accessibility
Free casino games are commonly accessible, permitting users from diverse locations to enjoy gambling.
No Monetary Obligation
Unlike money-based casino games, complimentary casino games do not demand a financial outlay. This facilitates users to play gaming without concerns about losing finances.
Sample Before Spending
No-cost casino games provide gamblers the possibility to sample casino activities before investing real cash. This aids players create well-thought-out choices.
Closing
Free-of-charge casino games offers a entertaining and non-risky means to engage in gambling. With free from financial burden, a wide variety of games, and possibilities for game mastery, it is no wonder that countless enthusiasts like free-of-charge casino games for their betting preferences.
Examining Real Money Slots
Commencement
Gambling slots have turned into a preferred selection for casino enthusiasts seeking the excitement of gaining real money. This piece delves into the benefits of gambling slots and the causes they are drawing increasing enthusiasts.
Perks of Gambling Slots
Real Winnings
The major attraction of gambling slots is the chance to win genuine currency. Unlike free-of-charge slots, real money slots give players the excitement of possible economic gains.
Large Game Selection
Gambling slots supply a broad variety of genres, attributes, and payout structures. This guarantees that there is an activity for every kind of gambler, ranging from classic three-reel classic slots to state-of-the-art animated slots with several winning lines and special bonuses.
Attractive Offers
Numerous online casinos supply attractive promotions for real money slot users. These can include initial offers, free spins, rebate offers, and loyalty programs. Such deals improve the entire playing activity and provide further possibilities to secure money.
Why Players Choose Real Money Slots
The Adrenaline of Gaining Genuine Funds
Real money slots provide an adrenaline-filled adventure, as gamblers await the possibility of winning actual cash. This aspect contributes a significant degree of excitement to the gaming activity.
Prompt Payouts
Real money slots supply gamblers the satisfaction of immediate payments. Gaining money quickly enhances the casino activity, making it more fulfilling.
Numerous Game Choices
With real money slots, players can play a diverse selection of slots, making sure that there is constantly a game different to experience.
Conclusion
Money slots provides a adrenaline-filled and satisfying gaming activity. With the potential to earn tangible currency, a wide range of games, and enticing offers, it’s no wonder that numerous players like money slots for their gaming choices.
bactrim 960mg for sale – buy levetiracetam 500mg generic tobramycin 5mg us
Pro88
Pro88
buy zovirax without a prescription – oral cerazette 0.075mg dydrogesterone order online
Консультация по стратегии продвижения сайтов продвижению.
Информация о том как взаимодействовать с низкочастотными ключевыми словами и как их подбирать
Тактика по действиям в конкурентоспособной нише.
Имею постоянных работаю с несколькими компаниями, есть что поделиться.
Посмотрите мой досье, на 31 мая 2024г
общий объём завершённых задач 2181 только здесь.
Консультация только устно, без скринов и отчетов.
Длительность консультации указано 2 часа, и реально всегда на связи без строгой привязки ко времени.
Как управлять с программным обеспечением это уже отдельная история, консультация по работе с программами оговариваем отдельно в другом услуге, определяем что нужно при коммуникации.
Всё спокойно на без напряжения не спеша
To get started, the seller needs:
Мне нужны сведения от телеграм чата для контакта.
коммуникация только вербально, вести переписку не хватает времени.
Сб и Воскресенье выходной
Definitely, what a fantastic blog and enlightening posts, I will bookmark your blog.All the Best!
Euro 2024
forxiga uk – order forxiga 10mg online cheap acarbose for sale online
UEFA EURO
One such software that has been generating buzz these days is the Lottery Defeater
luck365
purchase griseofulvin generic – buy lopid pills where can i buy lopid
bakar77
cheap vasotec 10mg – enalapril 5mg sale buy latanoprost generic
ทดลองเล่นสล็อต
Slotเว็บตรง – เพลิดเพลินกับการเล่นได้ทุกเครื่องมือที่ต่ออินเทอร์เน็ต
ในยุคนี้ การหมุนสล็อตมีความสะดวกมากยิ่งขึ้น คุณไม่จำเป็นต้องเดินทางไปยังบ่อนการพนันที่ไหน ๆ เพียงแค่มีอุปกรณ์อิเล็กทรอนิกส์ที่สามารถเชื่อมต่อกับอินเทอร์เน็ต คุณก็จะสนุกกับการเล่นสล็อตออนไลน์กับ PG Slot ได้จากทุกที่
การอัพเกรดเทคโนโลยีของ PG Slot
ที่ PG Slot เราได้สร้างสรรค์โซลูชั่นสำหรับการดูแลเกมคาสิโนออนไลน์เพื่อตอบสนองความต้องการของผู้เล่นให้มากที่สุด คุณไม่จำเป็นต้องติดตั้งโปรแกรมหรือนำมาใช้งานแอปพลิเคชันใด ๆ ให้น่าเบื่อหรือใช้หน่วยความจำในเครื่องมือของคุณ การดูแลเกมสล็อตออนไลน์ของเราดำเนินการผ่านเว็บตรงที่ใช้เทคโนโลยี HTML 5 ที่ทันยุค
ปั่นสล็อตได้ทุกอุปกรณ์เชื่อมต่อ
คุณมีโอกาสเล่นสล็อตออนไลน์กับ PG Slot ได้อย่างสะดวกเพียงเข้าสู่ในเว็บไซต์ของเรา เว็บตรงสล็อตออนไลน์ของเรารองรับทุกแพลตฟอร์มและทุกอุปกรณ์ทั้ง Android และ iOS ไม่ว่าคุณจะใช้โทรศัพท์ คอมพิวเตอร์ หรืออุปกรณ์พกพารุ่นไหน ก็จะมั่นใจได้ว่าคุณจะเล่นเกมสล็อตออนไลน์ได้อย่างไม่มีสะดุด ไม่มีความล่าช้าหรือกระตุกใด ๆ
ทดสอบเล่นสล็อตฟรี
เว็บตรงของเราเปิดให้บริการเพียงแค่คุณเข้ามาในเว็บไซต์ของ PG Slot ก็จะทดลองเล่นสล็อตฟรีได้ทันที ไม่ต้องเสียค่าธรรมเนียมใด ๆ นี่เป็นโอกาสที่ดีในการเรียนรู้และเรียนรู้เกี่ยวกับเกมก่อนที่จะลงเดิมพันด้วยเงินจริง
การเล่นเกมสล็อตออนไลน์กับ PG Slot ทำให้คุณมีโอกาสเพลิดเพลินกับการเล่นเกมคาสิโนได้ทุกที่ทุกเวลา ไม่ว่าคุณจะอยู่ที่ไหน เพียงแค่มีอุปกรณ์เชื่อมต่อที่ต่ออินเทอร์เน็ต คุณก็มีโอกาสสนุกกับการปั่นสล็อตได้อย่างไม่มีข้อจำกัด!
https://stixandstonz.ca/situs-slot-gacor
Somebody essentially help to make seriously posts I would state. This is the very first time I frequented your web page and thus far? I amazed with the research you made to create this particular publish amazing. Great job!
富遊娛樂城評價:2024年最新評價
推薦指數 : ★★★★★ ( 5.0/5 )
富遊娛樂城作為目前最受歡迎的博弈網站之一，在台灣擁有最高的註冊人數。
RG富遊以安全、公正、真實和順暢的品牌保證，贏得了廣大玩家的信賴。富遊線上賭場不僅提供了豐富多樣的遊戲種類，還有眾多吸引人的優惠活動。在出金速度方面，獲得無數網紅和網友的高度評價，確保玩家能享有無憂的博弈體驗。
推薦要點
新手首選: 富遊娛樂城，2024年評選首選，提供專為新手打造的豐富教學和獨家優惠。
一存雙收: 首存1000元，立獲1000元獎金，僅需1倍流水，新手友好。
免費體驗: 新玩家享免費體驗金，暢遊各式遊戲，開啟無限可能。
優惠多元: 活動豐富，流水要求低，適合各類型玩家。
玩家首選: 遊戲多樣，服務優質，是新手與老手的最佳賭場選擇。
富遊娛樂城詳情資訊
賭場名稱 : RG富遊
創立時間 : 2019年
賭場類型 : 現金版娛樂城
博弈執照 : 馬爾他牌照(MGA)認證、英屬維爾京群島(BVI)認證、菲律賓(PAGCOR)監督競猜牌照
遊戲類型 : 真人百家樂、運彩投注、電子老虎機、彩票遊戲、棋牌遊戲、捕魚機遊戲
存取速度 : 存款5秒 / 提款3-5分
軟體下載 : 支援APP，IOS、安卓(Android)
線上客服 : 需透過官方LINE
富遊娛樂城優缺點
優點
台灣註冊人數NO.1線上賭場
首儲1000贈1000只需一倍流水
擁有體驗金免費體驗賭場
網紅部落客推薦保證出金線上娛樂城
缺點
需透過客服申請體驗金
富遊娛樂城存取款方式
存款方式
提供四大超商(全家、7-11、萊爾富、ok超商)
虛擬貨幣ustd存款
銀行轉帳(各大銀行皆可)
取款方式
網站內申請提款及可匯款至綁定帳戶
現金1:1出金
富遊娛樂城平台系統
真人百家 — RG真人、DG真人、歐博真人、DB真人(原亞博/PM)、SA真人、OG真人、WM真人
體育投注 — SUPER體育、鑫寶體育、熊貓體育(原亞博/PM)
彩票遊戲 — 富遊彩票、WIN 539
電子遊戲 —RG電子、ZG電子、BNG電子、BWIN電子、RSG電子、GR電子(好路)
棋牌遊戲 —ZG棋牌、亞博棋牌、好路棋牌、博亞棋牌
電競遊戲 — 熊貓體育
捕魚遊戲 —ZG捕魚、RSG捕魚、好路GR捕魚、DB捕魚
dimenhydrinate 50mg tablet – actonel order risedronate 35 mg drug
You are a very intelligent individual!
barbar77
娛樂城排行
2024娛樂城推薦，經過玩家實測結果出爐Top5！
2024娛樂城排名是這五間上榜，玩家尋找娛樂城無非就是要找穩定出金娛樂城，遊戲體驗良好、速度流暢，Ace博評網都幫你整理好了，給予娛樂城新手最佳的指南，不再擔心被黑網娛樂城詐騙！
2024娛樂城簡述
在現代，2024娛樂城數量已經超越以前，面對琳瑯滿目的娛樂城品牌，身為新手的玩家肯定難以辨別哪間好、哪間壞。
好的平台提供穩定的速度與遊戲體驗，穩定的系統與資訊安全可以保障用戶的隱私與資料，不用擔心收到傳票與任何網路威脅，這些線上賭場也提供合理的優惠活動給予玩家。
壞的娛樂城除了會騙取你的金錢之外，也會打著不實的廣告、優惠滿滿，想領卻是一場空！甚至有些平台還沒辦法登入，入口網站也是架設用來騙取新手儲值進他們口袋，這些黑網娛樂城是玩家必須避開的風險！
評測2024娛樂城的標準
Ace這次從網路上找來五位使用過娛樂城資歷2年以上的老玩家，給予他們使用各大娛樂城平台，最終選出Top5，而評選標準為下列這些條件：
以玩家觀點出發，優先考量玩家利益
豐富的遊戲種類與卓越的遊戲體驗
平台的信譽及其安全性措施
客服團隊的回應速度與服務品質
簡便的儲值流程和多樣的存款方法
吸引人的優惠活動方案
前五名娛樂城表格
賭博網站排名 線上賭場 平台特色 玩家實測評價
No.1 富遊娛樂城 遊戲選擇豐富，老玩家優惠多 正面好評
No.2 bet365娛樂城 知名大廠牌，運彩盤口選擇多 介面流暢
No.3 亞博娛樂城 多語言支持，介面簡潔順暢 賽事豐富
No.4 PM娛樂城 撲克牌遊戲豐富，選擇多元 直播順暢
No.5 1xbet娛樂城 直播流暢，安全可靠 佳評如潮
線上娛樂城玩家遊戲體驗評價分享
網友A：娛樂城平台百百款，富遊娛樂城是我3年以來長期使用的娛樂城，別人有的系統他們都有，出金也沒有被卡過，比起那些玩娛樂城還會收到傳票的娛樂城，富遊真的很穩定，值得推薦。
網友B：bet365中文的介面簡約，還有超多體育賽事盤口可以選擇，此外賽事大部分也都有附上直播來源，不必擔心看不到賽事最新狀況，全螢幕還能夠下單，真的超方便！
網友C：富遊娛樂城除了第一次儲值有優惠之外，儲值到一定金額還有好禮五選一，實用又方便，有問題的時候也有客服隨時能夠解答。
網友D：從大陸來台灣工作，沒想到台灣也能玩到亞博體育，這是以前在大陸就有使用的平台，雖然不是簡體字，但使用介面完全沒問題，遊戲流暢、速度比以前使用還更快速。
網友E：看玖壹壹MV發現了PM娛樂城這個大品牌，PM的真人百家樂沒有輸給在澳門實地賭場，甚至根本不用出門，超級方便的啦！
https://fieldlineapps.ca/dragon4d
娛樂城
2024娛樂城介紹
台灣2024娛樂城越開越多間，新開的線上賭場層出不窮，每間都以獨家的娛樂城優惠和體驗金來吸引玩家，致力於提供一流的賭博遊戲體驗。以下來介紹這幾間娛樂城網友對他們的真實評價，看看哪些娛樂城上榜了吧！
2024娛樂城排名
2023下半年，各家娛樂城競爭激烈，相繼推出誘人優惠，不論是娛樂城體驗金、反水流水還是首儲禮金，甚至還有娛樂城抽I15手機。以下就是2024年網友推薦的娛樂城排名：
NO.1 富遊娛樂城
NO.2 Bet365台灣
NO.3 DG娛樂城
NO.4 九州娛樂城
NO.5 亞博娛樂城
2024娛樂城推薦
根據2024娛樂城排名，以下將富遊娛樂城、BET365、亞博娛樂城、九州娛樂城、王者娛樂城推薦給大家，包含首儲贈點、免費體驗金、存提款速度、流水等等…
娛樂城遊戲種類
線上娛樂城憑藉其廣泛的遊戲種類，成功滿足了各式各樣玩家的喜好和需求。這些娛樂城遊戲不僅多元化且各具特色，能夠為玩家提供無與倫比的娛樂體驗。下面是一些最受歡迎的娛樂城遊戲類型：
電子老虎機
魔龍傳奇、雷神之鎚、戰神呂布、聚寶財神、鼠來寶、皇家777
真人百家樂
真人視訊百家樂、牛牛、龍虎、炸金花、骰寶、輪盤
電子棋牌
德州撲克、兩人麻將、21點、十三支、妞妞、三公、鬥地主、大老二、牌九
體育下注
世界盃足球賽、NBA、WBC世棒賽、英超、英雄聯盟LOL、特戰英豪
線上彩票
大樂透、539、美國天天樂、香港六合彩、北京賽車
捕魚機遊戲
三仙捕魚、福娃捕魚、招財貓釣魚、西遊降魔、吃我一砲、賓果捕魚
2024娛樂城常見問題
娛樂城是什麼？
娛樂城/線上賭場(現金網)是台灣對於線上賭場的特別稱呼，而且是現金網，大家也許會好奇為什麼不直接叫做線上賭場或是線上博弈就好了。
其實這是有原因的，線上賭場這種東西，架站在台灣是違法的，在早期經營線上博弈被抓的風險非常高所以換了一個打模糊仗的代稱「娛樂城」來規避警方的耳目，畢竟以前沒有Google這種東西，這樣的代稱還是多少有些作用的。
信用版娛樂城是什麼？
信用版娛樂城是一種賭博平台，允許玩家在沒有預先充值的情況下參與遊戲。這種模式類似於信用卡，通常以周結或月結的方式結算遊戲費用。因此，如果玩家無法有效管理自己的投注額，可能會在月底面臨巨大的支付壓力。
娛樂城不出金怎麼辦？
釐清原因，如未違反娛樂城機制，可能是遇上黑網娛樂城，請盡快通報165反詐騙。
娛樂城
Player台灣線上娛樂城遊戲指南與評測
台灣最佳線上娛樂城遊戲的終極指南！我們提供專業評測，分析熱門老虎機、百家樂、棋牌及其他賭博遊戲。從遊戲規則、策略到選擇最佳娛樂城，我們全方位覆蓋，協助您更安全的遊玩。
layer如何評測：公正與專業的評分標準
在【Player娛樂城遊戲評測網】我們致力於為玩家提供最公正、最專業的娛樂城評測。我們的評測過程涵蓋多個關鍵領域，旨在確保玩家獲得可靠且全面的信息。以下是我們評測娛樂城的主要步驟：
安全與公平性
安全永遠是我們評測的首要標準。我們審查每家娛樂城的執照資訊、監管機構以及使用的隨機數生成器，以確保其遊戲結果的公平性和隨機性。
02.
遊戲品質與多樣性
遊戲的品質和多樣性對於玩家體驗至關重要。我們評估遊戲的圖形、音效、用戶介面和創新性。同時，我們也考量娛樂城提供的遊戲種類，包括老虎機、桌遊、即時遊戲等。
03.
娛樂城優惠與促銷活動
我們仔細審視各種獎勵計劃和促銷活動，包括歡迎獎勵、免費旋轉和忠誠計劃。重要的是，我們也檢查這些優惠的賭注要求和條款條件，以確保它們公平且實用。
04.
客戶支持
優質的客戶支持是娛樂城質量的重要指標。我們評估支持團隊的可用性、響應速度和專業程度。一個好的娛樂城應該提供多種聯繫方式，包括即時聊天、電子郵件和電話支持。
05.
銀行與支付選項
我們檢查娛樂城提供的存款和提款選項，以及相關的處理時間和手續費。多樣化且安全的支付方式對於玩家來說非常重要。
06.
網站易用性、娛樂城APP體驗
一個直觀且易於導航的網站可以顯著提升玩家體驗。我們評估網站的設計、可訪問性和移動兼容性。
07.
玩家評價與反饋
我們考慮真實玩家的評價和反饋。這些資料幫助我們了解娛樂城在實際玩家中的表現。
娛樂城常見問題
娛樂城是什麼？
娛樂城是什麼?娛樂城是台灣對於線上賭場的特別稱呼，線上賭場分為幾種：現金版、信用版、手機娛樂城(娛樂城APP)，一般來說，台灣人在稱娛樂城時，是指現金版線上賭場。
線上賭場在別的國家也有別的名稱，美國 – Casino, Gambling、中國 – 线上赌场,娱乐城、日本 – オンラインカジノ、越南 – Nhà cái。
娛樂城會被抓嗎？
在台灣，根據刑法第266條，不論是實體或線上賭博，參與賭博的行為可處最高5萬元罰金。而根據刑法第268條，為賭博提供場所並意圖營利的行為，可能面臨3年以下有期徒刑及最高9萬元罰金。一般賭客若被抓到，通常被視為輕微罪行，原則上不會被判處監禁。
信用版娛樂城是什麼？
信用版娛樂城是一種線上賭博平台，其中的賭博活動不是直接以現金進行交易，而是基於信用系統。在這種模式下，玩家在進行賭博時使用虛擬的信用點數或籌碼，這些點數或籌碼代表了一定的貨幣價值，但實際的金錢交易會在賭博活動結束後進行結算。
現金版娛樂城是什麼？
現金版娛樂城是一種線上博弈平台，其中玩家使用實際的金錢進行賭博活動。玩家需要先存入真實貨幣，這些資金轉化為平台上的遊戲籌碼或信用，用於參與各種賭場遊戲。當玩家贏得賭局時，他們可以將這些籌碼或信用兌換回現金。
娛樂城體驗金是什麼？
娛樂城體驗金是娛樂場所為新客戶提供的一種免費遊玩資金，允許玩家在不需要自己投入任何資金的情況下，可以進行各類遊戲的娛樂城試玩。這種體驗金的數額一般介於100元到1,000元之間，且對於如何使用這些體驗金以達到提款條件，各家娛樂城設有不同的規則。
在现代，在线赌场提供了多种便捷的存款和取款方式。对于较大金额的存款，您可以选择中国信托、台中银行、合作金库、台新银行、国泰银行或中华邮政。这些银行提供的服务覆盖金额范围从$1000到$10万，确保您的资金可以安全高效地转入赌场账户。
如果您需要进行较小金额的存款，可以选择通过便利店充值。7-11、全家、莱尔富和OK超商都提供这种服务，适用于金额范围在$1000到$2万之间的充值。通过这些便利店，您可以轻松快捷地完成资金转账，无需担心银行的营业时间或复杂的操作流程。
在进行娱乐场提款时，您可以选择通过各大银行转账或ATM转账。这些方法不仅安全可靠，而且非常方便，适合各种提款需求。最低提款金额为$1000，而上限则没有限制，确保您可以灵活地管理您的资金。
在选择在线赌场时，玩家评价和推荐也是非常重要的。许多IG网红和部落客，如丽莎、穎柔、猫少女日记-Kitty等，都对一些知名的娱乐场给予了高度评价。这些推荐不仅帮助您找到可靠的娱乐场所，还能确保您在游戏中享受到最佳的用户体验。
总体来说，在线赌场通过提供多样化的存款和取款方式，以及得到广泛认可的服务质量，正在不断吸引更多的玩家。无论您选择通过银行还是便利店进行充值，都能体验到快速便捷的操作。同时，通过查看玩家的真实评价和推荐，您也能更有信心地选择合适的娱乐场，享受安全、公正的游戏环境。
娛樂城
Player台灣線上娛樂城遊戲指南與評測
台灣最佳線上娛樂城遊戲的終極指南！我們提供專業評測，分析熱門老虎機、百家樂、棋牌及其他賭博遊戲。從遊戲規則、策略到選擇最佳娛樂城，我們全方位覆蓋，協助您更安全的遊玩。
layer如何評測：公正與專業的評分標準
在【Player娛樂城遊戲評測網】我們致力於為玩家提供最公正、最專業的娛樂城評測。我們的評測過程涵蓋多個關鍵領域，旨在確保玩家獲得可靠且全面的信息。以下是我們評測娛樂城的主要步驟：
安全與公平性
安全永遠是我們評測的首要標準。我們審查每家娛樂城的執照資訊、監管機構以及使用的隨機數生成器，以確保其遊戲結果的公平性和隨機性。
02.
遊戲品質與多樣性
遊戲的品質和多樣性對於玩家體驗至關重要。我們評估遊戲的圖形、音效、用戶介面和創新性。同時，我們也考量娛樂城提供的遊戲種類，包括老虎機、桌遊、即時遊戲等。
03.
娛樂城優惠與促銷活動
我們仔細審視各種獎勵計劃和促銷活動，包括歡迎獎勵、免費旋轉和忠誠計劃。重要的是，我們也檢查這些優惠的賭注要求和條款條件，以確保它們公平且實用。
04.
客戶支持
優質的客戶支持是娛樂城質量的重要指標。我們評估支持團隊的可用性、響應速度和專業程度。一個好的娛樂城應該提供多種聯繫方式，包括即時聊天、電子郵件和電話支持。
05.
銀行與支付選項
我們檢查娛樂城提供的存款和提款選項，以及相關的處理時間和手續費。多樣化且安全的支付方式對於玩家來說非常重要。
06.
網站易用性、娛樂城APP體驗
一個直觀且易於導航的網站可以顯著提升玩家體驗。我們評估網站的設計、可訪問性和移動兼容性。
07.
玩家評價與反饋
我們考慮真實玩家的評價和反饋。這些資料幫助我們了解娛樂城在實際玩家中的表現。
娛樂城常見問題
娛樂城是什麼？
娛樂城是什麼?娛樂城是台灣對於線上賭場的特別稱呼，線上賭場分為幾種：現金版、信用版、手機娛樂城(娛樂城APP)，一般來說，台灣人在稱娛樂城時，是指現金版線上賭場。
線上賭場在別的國家也有別的名稱，美國 – Casino, Gambling、中國 – 线上赌场,娱乐城、日本 – オンラインカジノ、越南 – Nhà cái。
娛樂城會被抓嗎？
在台灣，根據刑法第266條，不論是實體或線上賭博，參與賭博的行為可處最高5萬元罰金。而根據刑法第268條，為賭博提供場所並意圖營利的行為，可能面臨3年以下有期徒刑及最高9萬元罰金。一般賭客若被抓到，通常被視為輕微罪行，原則上不會被判處監禁。
信用版娛樂城是什麼？
信用版娛樂城是一種線上賭博平台，其中的賭博活動不是直接以現金進行交易，而是基於信用系統。在這種模式下，玩家在進行賭博時使用虛擬的信用點數或籌碼，這些點數或籌碼代表了一定的貨幣價值，但實際的金錢交易會在賭博活動結束後進行結算。
現金版娛樂城是什麼？
現金版娛樂城是一種線上博弈平台，其中玩家使用實際的金錢進行賭博活動。玩家需要先存入真實貨幣，這些資金轉化為平台上的遊戲籌碼或信用，用於參與各種賭場遊戲。當玩家贏得賭局時，他們可以將這些籌碼或信用兌換回現金。
娛樂城體驗金是什麼？
娛樂城體驗金是娛樂場所為新客戶提供的一種免費遊玩資金，允許玩家在不需要自己投入任何資金的情況下，可以進行各類遊戲的娛樂城試玩。這種體驗金的數額一般介於100元到1,000元之間，且對於如何使用這些體驗金以達到提款條件，各家娛樂城設有不同的規則。
娛樂城
在现代，在线赌场提供了多种便捷的存款和取款方式。对于较大金额的存款，您可以选择中国信托、台中银行、合作金库、台新银行、国泰银行或中华邮政。这些银行提供的服务覆盖金额范围从$1000到$10万，确保您的资金可以安全高效地转入赌场账户。
如果您需要进行较小金额的存款，可以选择通过便利店充值。7-11、全家、莱尔富和OK超商都提供这种服务，适用于金额范围在$1000到$2万之间的充值。通过这些便利店，您可以轻松快捷地完成资金转账，无需担心银行的营业时间或复杂的操作流程。
在进行娱乐场提款时，您可以选择通过各大银行转账或ATM转账。这些方法不仅安全可靠，而且非常方便，适合各种提款需求。最低提款金额为$1000，而上限则没有限制，确保您可以灵活地管理您的资金。
在选择在线赌场时，玩家评价和推荐也是非常重要的。许多IG网红和部落客，如丽莎、穎柔、猫少女日记-Kitty等，都对一些知名的娱乐场给予了高度评价。这些推荐不仅帮助您找到可靠的娱乐场所，还能确保您在游戏中享受到最佳的用户体验。
总体来说，在线赌场通过提供多样化的存款和取款方式，以及得到广泛认可的服务质量，正在不断吸引更多的玩家。无论您选择通过银行还是便利店进行充值，都能体验到快速便捷的操作。同时，通过查看玩家的真实评价和推荐，您也能更有信心地选择合适的娱乐场，享受安全、公正的游戏环境。
buy feldene 20 mg – rivastigmine sale order rivastigmine for sale
gowin123
buy generic etodolac – pletal 100 mg generic cilostazol 100mg cost
https://lnwsbobet2.com/?keyword=situstoto
สล็อตออนไลน์เว็บตรง: ความรื่นเริงที่ผู้เล่นไม่ควรพลาด
การเล่นเกมสล็อตในปัจจุบันได้รับความนิยมอย่างกว้างขวาง เนื่องจากความง่ายดายที่นักเดิมพันสามารถเล่นได้จากทุกหนทุกแห่งทุกเวลา โดยไม่ต้องเสียเวลาเดินทางไปยังสถานที่คาสิโนจริง ๆ ในบทความนี้ เราจะมาพูดถึง “สล็อตออนไลน์” และความบันเทิงที่คุณจะได้สัมผัสในเกมของเว็บตรง
ความสะดวกในการเล่นสล็อตออนไลน์
เหตุผลหนึ่งที่ทำให้สล็อตออนไลน์เว็บตรงเป็นที่ยอดนิยมอย่างยิ่ง คือความสะดวกที่ผู้เล่นมี คุณสามารถเล่นสล็อตได้ทุกหนทุกแห่งตลอดเวลา ไม่ว่าจะเป็นที่บ้านของคุณ ที่ทำงาน หรือถึงแม้จะอยู่ในการเดินทาง สิ่งที่คุณต้องมีคือเครื่องมือที่ต่ออินเทอร์เน็ตได้ ไม่ว่าจะเป็นโทรศัพท์มือถือ แท็บเล็ท หรือโน้ตบุ๊ก
นวัตกรรมกับสล็อตที่เว็บตรง
การเล่นเกมสล็อตในยุคนี้ไม่เพียงแต่สะดวก แต่ยังประกอบด้วยนวัตกรรมที่ทันสมัยอีกด้วย สล็อตที่เว็บตรงใช้นวัตกรรม HTML5 ซึ่งทำให้ท่านไม่ต้องกังวลเกี่ยวกับการลงโปรแกรมหรือแอปพลิเคชันเสริม แค่ใช้เบราว์เซอร์บนเครื่องมือของคุณและเข้ามายังเว็บไซต์ ผู้เล่นก็สามารถเริ่มเล่นเกมสล็อตได้ทันที
ตัวเลือกหลากหลายของเกมสล็อตออนไลน์
สล็อตที่เว็บตรงมาพร้อมกับความหลากหลายของเกมที่ท่านเลือกได้ ไม่ว่าจะเป็นเกมสล็อตแบบคลาสสิกหรือเกมที่มีฟีเจอร์ฟีเจอร์เพิ่มเติมและโบนัสเพียบ ผู้เล่นจะเห็นว่ามีเกมเลือกมากมาย ซึ่งทำให้ไม่เบื่อกับการเล่นสล็อต
การสนับสนุนทุกอุปกรณ์ที่ใช้
ไม่ว่าผู้เล่นจะใช้โทรศัพท์มือถือระบบ Androidหรือ iOS ท่านก็สามารถเล่นเกมสล็อตออนไลน์ได้อย่างไม่มีสะดุด เว็บของเราสนับสนุนระบบปฏิบัติการและทุกเครื่อง ไม่ว่าจะเป็นมือถือใหม่ล่าสุดหรือรุ่นเก่าแก่ หรือแม้กระทั่งแท็บเล็ตและแล็ปท็อป คุณก็สามารถเพลิดเพลินกับเกมสล็อตได้ได้อย่างครบถ้วน
ทดลองเล่นเกมสล็อต
สำหรับมือใหม่กับการเล่นสล็อตออนไลน์ หรือยังไม่แน่ใจเกี่ยวกับเกมที่ต้องการเล่น PG Slot ยังมีบริการทดลองเล่นสล็อตฟรี ท่านสามารถทดลองเล่นได้ทันทีโดยไม่ต้องสมัครสมาชิกหรือฝากเงิน การทดลองเล่นสล็อตนี้จะช่วยให้ท่านเรียนรู้วิธีการเล่นและเข้าใจวิธีการเล่นได้โดยไม่ต้องเสียค่าใช้จ่ายใด ๆ
โปรโมชั่นและโบนัสพิเศษ
หนึ่งในข้อดีของการเล่นเกมสล็อตกับ PG Slot คือมีโปรโมชันและโบนัสมากมายสำหรับผู้เล่น ไม่ว่าคุณจะเป็นสมาชิกเพิ่งสมัครหรือผู้เล่นเก่า ท่านสามารถได้รับโบนัสและโปรโมชันต่าง ๆ ได้อย่างต่อเนื่อง ซึ่งจะทำให้โอกาสชนะมากขึ้นและเพิ่มความสนุกในเกม
บทสรุป
การเล่นสล็อตออนไลน์ที่ PG Slot เป็นการการลงทุนทางเกมที่คุ้มค่า ท่านจะได้รับความสนุกและความสะดวกจากการเล่นสล็อต นอกจากนี้ยังมีโอกาสลุ้นรับรางวัลและโบนัสเพียบ ไม่ว่าผู้เล่นจะใช้โทรศัพท์มือถือ แท็บเล็ทหรือแล็ปท็อปรุ่นใด ก็สามารถเริ่มเล่นกับเราได้ทันที อย่ารอช้า เข้าร่วมและเริ่มสนุกกับ PG Slot วันนี้
pg slot
สล็อตตรงจากเว็บ — ใช้ได้กับ โทรศัพท์มือถือ แท็บเลต คอมพิวเตอร์ส่วนตัว ฯลฯ สำหรับการเล่น
ระบบสล็อตเว็บโดยตรง ของ พีจีสล็อต ได้รับการพัฒนาและปรับแต่ง เพื่อให้ รองรับการใช้งาน บนอุปกรณ์ที่หลากหลายได้อย่าง สมบูรณ์ ไม่สำคัญว่าจะใช้ สมาร์ทโฟน แท็บเลต หรือ คอมพิวเตอร์ รุ่นไหน
ที่ PG Slot เราเข้าใจถึงสิ่งที่ผู้เล่นต้องการ จากผู้เล่น ในเรื่อง การใช้งานง่าย และ การเข้าถึงเกมคาสิโนที่รวดเร็ว เราจึง นำ HTML 5 มาใช้ ซึ่งเป็น เทคโนโลยีที่ล้ำสมัย ในตอนนี้ มาใช้พัฒนาเว็บไซต์ คุณจึงไม่ต้อง โหลดแอป หรือติดตั้งโปรแกรมเพิ่มเติม เพียง เปิดบราวเซอร์ บนอุปกรณ์ที่ คุณใช้อยู่ และเยี่ยมชม เว็บไซต์ของเรา คุณสามารถ สนุกกับสล็อตได้ทันที
การใช้งานกับอุปกรณ์หลากหลาย
ไม่ว่าคุณจะใช้ สมาร์ทโฟน ระบบ Android หรือ ไอโอเอส ก็สามารถ เล่นสล็อตได้อย่างราบรื่น ระบบของเรา ออกแบบมาให้รองรับ ทุกระบบปฏิบัติการ ไม่สำคัญว่าคุณ มี โทรศัพท์ รุ่นใหม่หรือรุ่นเก่า หรือ แท็บเล็ตหรือโน้ตบุ๊ก ทุกอย่างก็สามารถ ใช้งานได้ดี ไม่มีปัญหา ในเรื่องความเข้ากันได้
สามารถเล่นได้ทุกที่ทุกเวลา
หนึ่งในข้อดีของการเล่นสล็อตกับ PG Slot คือ คุณสามารถ เล่นได้ทุกเวลา ไม่ว่าจะ อยู่ที่บ้าน ออฟฟิศ หรือแม้แต่ ในที่สาธารณะ สิ่งที่คุณต้องมีคือ การเชื่อมต่ออินเทอร์เน็ต คุณสามารถ เริ่มเล่นได้ทันที และคุณไม่ต้อง ห่วงเรื่องการดาวน์โหลด หรือติดตั้งโปรแกรมที่ ใช้พื้นที่ในอุปกรณ์
เล่นสล็อตฟรี
เพื่อให้ ผู้เล่นที่ใหม่ มีโอกาสลองและสัมผัสประสบการณ์สล็อตแมชชีนของเรา PG Slot ยังมีบริการสล็อตฟรี คุณสามารถ เล่นได้ทันทีโดยไม่ต้องสมัครสมาชิกหรือฝากเงิน การ เล่นฟรีนี้จะช่วยให้คุณเข้าใจวิธีเล่นและรู้จักเกมก่อนลงเดิมพันจริง
การบริการและความปลอดภัย
PG Slot มุ่งมั่นที่จะให้บริการที่ดีที่สุดแก่ลูกค้า เรามี ทีมงานมืออาชีพพร้อมให้บริการและช่วยเหลือคุณตลอด 24 ชั่วโมง นอกจากนี้เรายังมี ระบบรักษาความปลอดภัยที่ทันสมัย ด้วยวิธีนี้ คุณจึงมั่นใจได้ว่า ข้อมูลส่วนตัวและการเงินของคุณจะปลอดภัย
โปรโมชันและโบนัส
ข้อดีอีกประการของการเล่นสล็อตแมชชีนกับ PG Slot ก็คือ มี โปรโมชันและโบนัสมากมาย ไม่ว่าคุณจะเป็น ผู้เล่นใหม่หรือเก่า คุณสามารถ รับโปรโมชันและโบนัสได้ สิ่งนี้จะ เพิ่มโอกาสชนะและสนุกกับเกมมากขึ้น
สรุปการเล่นสล็อตเว็บที่ PG Slot ถือเป็นการลงทุนที่คุ้มค่า คุณจะไม่เพียงได้รับความสุขและความสะดวกสบายจากเกมเท่านั้น แต่คุณยังมีโอกาสลุ้นรับรางวัลและโบนัสมากมายอีกด้วย ไม่สำคัญว่าจะใช้โทรศัพท์มือถือ แท็บเล็ต หรือคอมพิวเตอร์รุ่นใด สามารถมาร่วมสนุกกับเราได้เลยตอนนี้ อย่ารอช้า ลงทะเบียนและเริ่มเล่นสล็อตกับ PG Slot วันนี้!
pg สล็อต
สำหรับ ไซต์ PG Slots ซึ่งมีการ มี ประโยชน์ หลายประการ เมื่อเทียบกับ คาสิโนแบบ ทั่วไป, โดยเฉพาะอย่างยิ่ง ใน ปัจจุบันนี้. ประโยชน์สำคัญ เหล่านี้ ตัวอย่างเช่น:
ความง่ายสะดวก: คุณ สามารถเข้าร่วม สล็อตออนไลน์ได้ ตลอด 24 ชั่วโมง จาก ทุกที่, ช่วย ผู้เล่นสามารถ ทดลอง ได้ ทุกแห่ง ไม่ต้อง เสียเวลา ไปคาสิโนแบบ ดั้งเดิม ๆ
เกมหลากหลายรูปแบบ: สล็อตออนไลน์ นำเสนอ รูปแบบเกม ที่ มากมาย, เช่น สล็อตรูปแบบคลาสสิค หรือ สล็อต ที่มี คุณสมบัติ และประโยชน์ พิเศษ, ไม่ทำ ความเซ็ง ในเกม
โปรโมชั่น และค่าตอบแทน: สล็อตออนไลน์ แทบจะ ให้ โปรโมชั่น และรางวัล เพื่อเพิ่ม ความเป็นไปได้ ในการ รับรางวัล และ เพิ่ม ความเพลิดเพลิน ให้กับเกม
ความปลอดภัย และ ความเชื่อถือได้: สล็อตออนไลน์ โดยทั่วไป มีการ การป้องกัน ที่ เหมาะสม, และ พึ่งพาได้ ว่า ข้อมูลลับ และ การเงิน จะได้รับการ คุ้มครอง
บริการสนับสนุน: PG Slots มี ผู้เชี่ยวชาญ มืออาชีพ ที่มุ่งมั่น ดูแล ตลอดเวลา
การเล่นบนมือถือ: สล็อต PG อนุญาต การเล่นบนอุปกรณ์เคลื่อนที่, ให้ ผู้เล่นสามารถทดลอง ตลอดเวลา
ทดลองเล่นโดยไม่เสียค่าใช้จ่าย: ของ ผู้เล่นใหม่, PG ยังให้บริการ เล่นทดลองฟรี เพิ่มเติมด้วย, เพื่อให้ ผู้เล่น ลองใช้ การเล่น และเรียนรู้ เกมก่อน เล่นด้วยเงินจริง
สล็อต PG มีคุณลักษณะ ประโยชน์ เป็นจำนวนมาก ที่ ช่วย ให้ได้รับความนิยม ในวันนี้, ทำให้ ระดับ ความสนุกสนาน ให้กับเกมด้วย.
ทดลองเล่นสล็อต
ทดลองปฏิบัติเล่นสล็อต และค้นพบประสบการณ์การเล่นเกมที่ไม่เหมือนใคร!
สำหรับนักพนันที่กำลังพิจารณาความบันเทิงและโอกาสในการได้รับรางวัลมหาศาล สล็อตออนไลน์เป็นอีกหนึ่งทางเลือกที่คุ้มค่าศึกษา.ด้วยความจำนวนมากของเกมสล็อตที่น่าตื่นเต้น ผู้เล่นสามารถปฏิบัติและค้นหาเกมที่ชื่นชอบได้อย่างง่ายดาย.
ไม่ว่าคุณจะประทับใจเกมสล็อตคลาสสิกหรือต้องการความแปลกใหม่, ตัวเลือกรอต้อนรับให้คุณสัมผัส. จากสล็อตที่มีแบบมากมาย ไปจนถึงเกมที่มีคุณสมบัติพิเศษและรางวัล, ผู้เล่นจะได้พบกับประสบการณ์ใหม่ที่น่าตื่นเต้นและน่าติดตาม.
ด้วยการทดสอบสล็อตฟรี, คุณสามารถศึกษาวิธีการเล่นและค้นตัดสินใจกลยุทธ์ที่ต้องการก่อนเริ่มลงเดิมพันด้วยเงินจริง. นี่คือโอกาสดีที่จะทำความคุ้นเคยกับเกมและเพิ่มโอกาสในการคว้ารางวัลใหญ่.
อย่าเลื่อนเวลา, ร่วมกับการปฏิบัติสล็อตออนไลน์วันนี้ และค้นพบประสบการณ์การเล่นเกมที่ไม่เหมือนใคร! เพลิดเพลินกับความน่าสนใจ, ความสนุกสนาน และโอกาสชนะรางวัลมากมาย. ทำก้าวแรกเดินทางสู่ความสำเร็จของคุณในวงการสล็อตออนไลน์แล้ววันนี้!
ลอง เล่น สล็อต PG ไปพร้อมกับ เข้าไปสู่ มุ่งสู่ ศักดิ์ศรี แห่ง ความบันเทิง ที่ ไม่มีที่สิ้นสุด
เกี่ยวกับ นักเสี่ยงโชค ที่ พยายาม ตามหา อารมณ์ เกมใหม่, สล็อต PG ถูกมองว่า ตัวเลือก ที่ น่าสนใจ เป็นอย่างมาก. เนื่องจาก ความหลากหลายของ ของ เกมสล็อตมากมาย ที่ น่าทึ่ง และ น่าทำความรู้จัก, นักพนัน จะสามารถ ทดสอบ และ ค้นพบ รูปแบบเกม ที่ ตรงกับ ความชอบการเล่น ของตนเอง.
ไม่ว่า คุณ จะชื่นชอบ ความผ่อนคลาย ที่คุ้นเคย หรือ การท้าทาย ที่ไม่เคยพบเจอ, สล็อต PG มี ที่หลากหลาย. ตั้งแต่ สล็อตประเภทคลาสสิก ที่ รู้จัก ไปจนถึง ตัวเกม ที่ มีลักษณะ ลักษณะพิเศษ และ โบนัสมากมาย, ผู้เล่น จะได้ พบเจอ ประสบการณ์การเล่น ที่ ดึงดูดใจ และ ตื่นเต้น
อันเนื่องมาจาก การทดสอบเล่น สล็อต PG ฟรีโดยไม่ต้องลงทุน, คุณ จะสามารถ ศึกษา วิธีการเล่น และ ทดสอบ กลวิธี ต่างๆ ก่อน เริ่มลงเดิมพัน ด้วยเงินจริง. นี่ ถือเป็น ทางเลือก อันดี ที่จะ วางแผน และ ปรับปรุง ความสามารถ ในการ ได้รับรางวัล รางวัลสูง.
อย่าชักช้า, เข้าถึง ในการ การลองเล่น สล็อต PG วันนี้ และ พบเจอ การเล่น ที่ ไร้ขีดจำกัด! รับรู้ ความตื่นเต้น, ความเพลิดเพลินใจ และ ความเป็นไปได้ ในการ ได้รับรางวัล มหาศาล. เริ่มต้น ทำ สู่ ความสมหวัง ของคุณในวงการ การพนันสล็อต เดี๋ยวนี้!
ทดสอบเล่นสล็อต PG ซื้อรอบหมุนฟรี
ในปัจจุบันนี้ การเล่นสล็อตออนไลน์ได้รับความสนใจอย่างมาก อย่างเฉพาะเจาะจงเกมสล็อตจากผู้ผลิต PG Slot ที่มีคุณสมบัติพิเศษมากมายให้ผู้เล่นได้สนุกสนาน หนึ่งในลักษณะพิเศษที่น่าสนใจและทำให้การปั่นสนุกยิ่งขึ้นคือ “การซื้อฟรีสปิน” ซึ่งเป็นการเพิ่มโอกาสในการชนะและเพิ่มความเร้าใจในการเล่น
ซื้อฟรีสปินคืออะไร
การซื้อตัวเลือกหมุนฟรีคือการที่นักพนันสามารถซื้อช่องทางในการหมุนวงล้อสล็อตโดยไม่ต้องรอให้เกิดไอคอนฟรีสปินบนวงล้อ ซึ่งเป็นการเพิ่มโอกาสในการได้รับรางวัลพิเศษต่างๆ ภายในเกม เช่น รางวัลโบนัส แจ็คพอต และอื่นๆ นอกจากนี้ การซื้อฟรีสปินยังช่วยให้ผู้เล่นสามารถเพิ่มจำนวนเงินที่ได้ได้อย่างรวดเร็วและมีมีผลดี
ผลดีของการทดสอบเล่นสล็อต PG ซื้อการหมุนฟรี
เพิ่มโอกาสในการชนะ: การซื้อตัวเลือกหมุนฟรีช่วยให้ผู้เล่นมีโอกาสสำเร็จในการได้รับของขวัญมากขึ้น จากที่มีการหมุนวงล้อฟรีเพิ่มเติม ซึ่งอาจนำพาไปถึงการได้รับแจ็คพอตหรือรางวัลโบนัสพิเศษอื่นๆ
ลดเวลาในการเล่น: การซื้อฟรีสปินช่วยประหยัดเวลาในการเล่นในการเล่น จากที่ไม่ต้องรอให้เกิดสัญญาณฟรีสปินบนวงล้อ ผู้ใช้งานสามารถเข้าโหมดฟรีสปินได้ทันที
ลองหมุนฟรี: สำหรับผู้ใช้งานที่ยังไม่แน่ใจเกี่ยวกับเกม PG Slot ยังมีตัวเลือกทดลองเล่นฟรีผู้เล่นได้ทดสอบเล่นและศึกษาเกมก่อนที่จะเลือกที่จะซื้อฟรีสปินด้วยเงินจริง
เพิ่มความสนุกสนาน: การซื้อตัวเลือกการหมุนฟรีช่วยเพิ่มความรื่นรมย์ในการเล่น เพราะว่านักพนันสามารถเข้าถึงรอบโบนัสและฟีเจอร์พิเศษอื่นๆ ได้อย่างง่ายดาย
วิธีการทำการซื้อฟรีสปินในสล็อต PG
เลือกเกมที่อยากเล่นจากค่าย PG Slot
คลิกที่ปุ่ม “ซื้อฟรีสปิน” ที่แสดงผลบนหน้าจอการเล่น
ใส่จำนวนฟรีสปินที่ต้องการใช้และยืนยันการสั่งซื้อ
เริ่มต้นการหมุนวงล้อและเพลิดเพลินกับการเล่น
บทสรุป
การลองเล่นสล็อต PGและการซื้อตัวเลือกการหมุนฟรีเป็นวิธีที่ดีในการเพิ่มโอกาสสำเร็จในการชนะและเพิ่มความสนุกในการเล่น ด้วยลักษณะพิเศษพิเศษนี้ นักเล่นสามารถเข้าสู่รอบโบนัสและคุณลักษณะพิเศษพิเศษต่างๆ ได้อย่างไวและมีประสิทธิผล ไม่ว่าคุณคือผู้เล่นใหม่เอี่ยมหรือผู้เล่นที่มีประสบการณ์ การสำรวจเล่นสล็อต PGและการซื้อตัวเลือกฟรีสปินจะช่วยให้คุณมีประสบการณ์ในการหมุนที่น่าตื่นตาตื่นใจและรื่นรมย์มากยิ่งขึ้น
ทดลองเล่นสล็อต PG ซื้อหมุนฟรี แล้วคุณจะพบกับความสนุกสนานและโอกาสในการชนะที่ไม่มีที่สิ้นสุด
ทดลองเล่นสล็อต pg เว็บ ตรง
การเผชิญหน้าการทดลองเล่นสล็อตแมชชีน PG บนแพลตฟอร์มเดิมพันโดยตรง: เปิดจักรวาลแห่งความตื่นเต้นที่ไร้ขีดจำกัด
ในกรณีของนักเสี่ยงทายที่กำลังมองหาการพบเจอเกมที่ไม่เหมือนใคร และต้องการเจอแหล่งเสี่ยงโชคที่มีความน่าเชื่อถือ, การทดลองเกมสล็อต PG บนแพลตฟอร์มตรงนับว่าตัวเลือกที่น่าประทับใจอย่างมาก. ด้วยความแตกต่างของเกมสล็อตที่มีให้เลือกเล่นมากมาย, ผู้เล่นจะได้ประสบกับโลกแห่งความตื่นเต้นเร้าใจและความสนุกสนานที่ไม่มีข้อจำกัด.
เว็บการเดิมพันโดยตรงนี้ มอบประสบการณ์การเล่นเกมพนันที่ปลอดภัยแน่นอน เชื่อถือได้ และสนองตอบความต้องการของนักพนันได้เป็นอย่างดี. ไม่ว่าผู้เล่นจะท่านจะติดใจสล็อตแมชชีนแนวคลาสสิกที่คุ้นเคย หรือต้องการประสบการณ์เกมใหม่ๆที่มีฟีเจอร์เฉพาะตัวและรางวัลล้นหลาม, แพลตฟอร์มโดยตรงนี้ก็มีให้คัดสรรอย่างหลากหลายชนิด.
อันเนื่องมาจากระบบการลองเล่นสล็อต PG ไม่มีค่าใช้จ่าย, ผู้เล่นจะได้โอกาสที่ดีศึกษาวิธีการเล่นเกมพนันและสำรวจเทคนิคหลากหลาย ก่อนจะเริ่มวางเดิมพันโดยใช้เงินจริง. การกระทำนี้นับว่าโอกาสอันดีที่สุดที่จะเพิ่มความพร้อมเพรียงและเสริมโอกาสในการได้รางวัลมหาศาลใหญ่.
ไม่ว่าผู้เล่นจะผู้เล่นจะอยากได้ความสนุกแบบดั้งเดิม หรือความท้าทายแปลกใหม่, เกมสล็อตแมชชีน PG บนแพลตฟอร์มเดิมพันโดยตรงก็มีให้คัดสรรอย่างหลากหลายชนิด. คุณอาจจะได้เผชิญกับการทดลองเล่นการเล่นเดิมพันที่น่าตื่นเต้นเร้าใจ เร้าใจ และสนุกสนานไปกับโอกาสที่ดีในการได้รับโบนัสมหาศาล.
อย่าลังเล, ร่วมสนุกทดลองเล่นเกมสล็อต PG บนเว็บเสี่ยงโชคไม่ผ่านเอเย่นต์วันนี้ และเจอโลกแห่งความสุขที่ปลอดภัยแน่นอน น่าสนใจ และมีแต่ความเพลิดเพลินรอคอยท่าน. ประสบความตื่นเต้น, ความสุข และโอกาสในการได้รับรางวัลมหาศาล. เริ่มการเดินทางเข้าสู่การเป็นผู้ชนะในวงการเกมออนไลน์วันนี้!
ทดลองเล่นสล็อต pg ฟรี
สล็อตเว็บโดยตรง — ใช้ โทรศัพท์มือถือ แท็บเล็ต คอมพิวเตอร์ส่วนตัว ฯลฯ เพื่อเล่น
ระบบสล็อตเว็บตรง ของ พีจีสล็อต ได้รับการพัฒนาและอัปเดต เพื่อให้ สามารถใช้งาน บนอุปกรณ์ที่หลากหลายได้อย่าง เต็มที่ ไม่สำคัญว่าจะใช้ สมาร์ทโฟน แท็บเล็ต หรือ คอมพิวเตอร์ส่วนตัว รุ่นใด
ที่ PG Slot เราเข้าใจถึงความต้องการ ของลูกค้า ในเรื่อง การใช้งานง่าย และ ความรวดเร็วในการเข้าถึงเกมคาสิโนออนไลน์ เราจึง นำ HTML 5 มาใช้ ซึ่งเป็น เทคโนโลยีที่ทันสมัยที่สุด ในตอนนี้ มาพัฒนาเว็บไซต์ของเรากันเถอะ คุณจึงไม่ต้อง ดาวน์โหลดแอป หรือติดตั้งโปรแกรมเพิ่มเติม เพียง เปิดเบราว์เซอร์ บนอุปกรณ์ที่ คุณมีอยู่ และเยี่ยมชม เว็บของเรา คุณสามารถ สนุกกับสล็อตได้ทันที
การใช้งานกับอุปกรณ์หลากหลาย
ไม่ว่าคุณจะใช้ มือถือ ระบบ แอนดรอยด์ หรือ ไอโอเอส ก็สามารถ เล่นสล็อตออนไลน์ได้ไม่มีสะดุด ระบบของเรา ได้รับการออกแบบให้รองรับ ทุกระบบปฏิบัติการ ไม่สำคัญว่าคุณ ใช้ โทรศัพท์ รุ่นใหม่หรือรุ่นเก่า หรือ แม้แต่แท็บเล็ตหรือแล็ปท็อป ทุกอย่างก็สามารถ ใช้งานได้ ไม่มีปัญหา เรื่องความเข้ากันได้
เล่นได้ทุกที่ทุกเวลา
หนึ่งในข้อดีของการเล่นสล็อตกับ PG Slot คือ คุณสามารถ เล่นได้ทุกที่ทุกเวลา ไม่ว่าจะ ที่บ้าน ออฟฟิศ หรือแม้แต่ ในที่สาธารณะ สิ่งที่คุณต้องมีคือ อินเทอร์เน็ต คุณสามารถ เริ่มเล่นได้ทันที และคุณไม่ต้อง ห่วงเรื่องการดาวน์โหลด หรือติดตั้งโปรแกรมที่ ใช้พื้นที่ในอุปกรณ์
ลองเล่นสล็อตแมชชีนฟรี
เพื่อให้ ผู้เล่นใหม่ มีโอกาสลองและสัมผัสประสบการณ์สล็อตแมชชีนของเรา PG Slot ยังมีบริการสล็อตฟรี คุณสามารถ ทดลองเล่นได้ทันทีโดยไม่ต้องสมัครหรือฝากเงิน การ ทดลองเล่นสล็อตแมชชีนฟรีนี้จะช่วยให้คุณเรียนรู้วิธีเล่นและเข้าใจเกมก่อนตัดสินใจเดิมพันด้วยเงินจริง
การบริการและความปลอดภัย
PG Slot ตั้งใจให้บริการที่ดีที่สุดกับลูกค้า เรามี ทีมงานมืออาชีพพร้อมให้บริการและช่วยเหลือคุณตลอด 24 ชั่วโมง นอกจากนี้เรายังมี ระบบรักษาความปลอดภัยที่ทันสมัย ด้วยวิธีนี้ คุณจึงมั่นใจได้ว่า ข้อมูลและการเงินของคุณจะปลอดภัย
โปรโมชั่นและของรางวัลพิเศษ
การเล่นสล็อตกับ PG Slot ยังมีข้อดี นั่นคือ มี โปรโมชั่นและโบนัสพิเศษมากมายสำหรับผู้เข้าร่วม ไม่ว่าคุณจะเป็น ผู้เล่นใหม่หรือเก่า คุณสามารถ รับโปรโมชันและโบนัสได้เรื่อย ๆ สิ่งนี้จะ เพิ่มโอกาสชนะและความสนุกในเกม
สรุปการเล่นสล็อตเว็บที่ PG Slot ถือเป็นการลงทุนที่คุ้มค่า คุณจะไม่เพียงได้รับความสุขและความสะดวกสบายจากเกมเท่านั้น แต่คุณยังมีโอกาสลุ้นรับรางวัลและโบนัสมากมายอีกด้วย ไม่สำคัญว่าจะใช้โทรศัพท์มือถือ แท็บเล็ต หรือคอมพิวเตอร์รุ่นใด สามารถมาร่วมสนุกกับเราได้เลยตอนนี้ อย่ารอช้า ลงทะเบียนและเริ่มเล่นสล็อตกับ PG Slot วันนี้!
hk paito warna
ทดลองทดสอบเล่นสล็อต และค้นพบประสบการณ์การเล่นเกมที่ไม่เหมือนใคร!
สำหรับนักพนันที่กำลังต้องการความบันเทิงและโอกาสในการชนะรางวัลมหาศาล สล็อตออนไลน์เป็นอีกหนึ่งโอกาสที่คุ้มค่าใช้.ด้วยความมากมายของเกมสล็อตที่น่าตื่นเต้น ผู้เล่นสามารถทดสอบและค้นหาเกมที่ถูกใจได้อย่างง่ายดาย.
ไม่ว่าคุณจะชอบเกมสล็อตคลาสสิกหรือต้องการความท้าทายใหม่, ทางเลือกมากมายรอล้ำหน้าให้คุณสัมผัส. จากสล็อตที่มีหัวข้อมากมาย ไปจนถึงเกมที่มีฟีเจอร์พิเศษและรางวัล, ผู้เล่นจะได้พบกับการเล่นเกมที่น่าตื่นเต้นและน่าติดตาม.
ด้วยการทดลองเล่นสล็อตฟรี, คุณสามารถปฏิบัติวิธีการเล่นและค้นตัดสินใจกลยุทธ์ที่ถูกใจก่อนลงทุนด้วยเงินจริง. นี่คือโอกาสที่ดีที่จะศึกษากับเกมและเพิ่มโอกาสในการชนะรางวัลใหญ่.
อย่าเลื่อนเวลา, เข้าร่วมกับการลองเล่นสล็อตออนไลน์วันนี้ และค้นพบประสบการณ์การเล่นเกมที่ไม่เหมือนใคร! สัมผัสความสนใจ, ความยินดี และโอกาสในการชนะรางวัล. ทำก้าวแรกเดินทางสู่ความเฟื่องฟูของคุณในวงการสล็อตออนไลน์แล้ววันนี้!
My brother recommended I would possibly like this web site. He was entirely right. This post actually made my day. You can not believe simply how so much time I had spent for this info! Thanks!
הימורים באינטרנט
הימורי ספורט – הימור באינטרנט
הימורי ספורטיביים נהיו לאחד הענפים המתפתחים ביותר בהימורים באינטרנט. שחקנים מסוגלים להתערב על תוצאותיהם של אירועי ספורט פופולריים לדוגמה כדור רגל, כדור סל, משחק הטניס ועוד. האופציות להימור הן מרובות, וביניהן תוצאת ההתמודדות, מספר הגולים, כמות הנקודות ועוד. להלן דוגמאות של למשחקים נפוצים במיוחד עליהם ניתן להמר:
כדורגל: ליגת האלופות, גביע העולם, ליגות אזוריות
כדורסל: NBA, ליגת יורוליג, טורנירים בינלאומיים
משחק הטניס: ווימבלדון, US Open, רולאן גארוס
פוקר ברשת ברשת – הימור באינטרנט
פוקר ברשת הוא אחד מהמשחקים ההימור המוכרים ביותר בימינו. שחקנים מסוגלים להתמודד נגד יריבים מכל רחבי העולם בסוגי וריאציות משחק , למשל טקסס הולדם, אומהה, Stud ועוד. אפשר לגלות טורנירים ומשחקי קש במבחר רמות ואפשרויות מגוונות. אתרי פוקר המובילים מציעים גם:
מבחר רב של וריאציות פוקר
טורנירים שבועיות וחודשיות עם פרסים כספיים גבוהים
שולחנות למשחקים מהירים ולטווח הארוך
תוכניות נאמנות ומועדוני VIP עם הטבות יחודיות
בטיחות ואבטחה והוגנות
כאשר הבחירה פלטפורמה להימורים ברשת, חשוב לבחור אתרי הימורים מורשים המפוקחים המציעים גם סביבה למשחק מאובטחת והוגנת. אתרים אלו משתמשים בטכנולוגיות הצפנה מתקדמות להגנה על נתונים אישיים ופיננסיים, וגם באמצעות תוכנות גנרטור מספרים רנדומליים (RNG) כדי להבטיח הגינות במשחקים במשחקים.
בנוסף, הכרחי לשחק בצורה אחראית תוך קביעת מגבלות אישיות הימור אישיות. מרבית האתרים מאפשרים גם לשחקנים לקבוע מגבלות הפסד ופעילות, וגם לנצל כלים למניעת התמכרות. שחקו בתבונה ואל תרדפו גם אחרי הפסד.
המדריך השלם לקזינו ברשת, הימורי ספורט ופוקר באינטרנט ברשת
הימורים באינטרנט מציעים גם עולם שלם הזדמנויות מרתקות לשחקנים, מתחיל מקזינו אונליין וגם בהימורי ספורט ופוקר ברשת. בעת בחירת בפלטפורמת הימורים, חשוב לבחור אתרים מפוקחים המציעים גם סביבת משחק מאובטחת והגיונית. זכרו לשחק תמיד בצורה אחראית תמיד ואחראי – משחקי ההימורים ברשת אמורים להיות מבדרים ולא גם ליצור לבעיות פיננסיות או חברתיים.
הימורי ספורט – הימורים באינטרנט
הימור ספורט נעשו לאחד התחומים המתפתחים ביותר בהימור ברשת. שחקנים יכולים להתערב על תוצאות של אירועים ספורטיביים פופולריים כמו כדור רגל, כדורסל, משחק הטניס ועוד. האופציות להתערבות הן מרובות, וביניהן תוצאת המשחק, מספר השערים, כמות הנקודות ועוד. הבא דוגמאות למשחקי נפוצים במיוחד עליהם ניתן להמר:
כדורגל: ליגת האלופות, גביע העולם, ליגות אזוריות
כדור סל: ליגת NBA, ליגת יורוליג, תחרויות בינלאומיות
משחק הטניס: ווימבלדון, אליפות ארה”ב הפתוחה, אליפות צרפת הפתוחה
פוקר באינטרנט – הימור ברשת
פוקר באינטרנט הוא אחד ממשחקי ההימורים הפופולריים ביותר בימינו. שחקנים יכולים להתחרות מול יריבים מרחבי תבל במגוון סוגי של המשחק , למשל טקסס הולדם, אומהה, Stud ועוד. ניתן למצוא טורנירים ומשחקי קש במבחר דרגות ואפשרויות הימור מגוונות. אתרי הפוקר המובילים מציעים:
מגוון רחב של גרסאות המשחק פוקר
טורנירים שבועיים וחודשיים עם פרסים כספיים גבוהים
שולחנות למשחקים מהירים ולטווח ארוך
תוכניות נאמנות ללקוחות ומועדוני VIP VIP עם הטבות
בטיחות והוגנות
בעת בוחרים פלטפורמה להימורים ברשת, חיוני לבחור גם אתרי הימורים מורשים ומפוקחים המציעים סביבת משחק בטוחה והוגנת. אתרים אלו משתמשים בטכנולוגיות הצפנה מתקדמות להבטחה על מידע אישי ופיננסי, וכן בתוכנות מחולל מספרים אקראיים (RNG) כדי לוודא הגינות המשחקים במשחקים.
מעבר לכך, חשוב לשחק באופן אחראי תוך כדי קביעת מגבלות הימור אישיות של השחקן. רוב אתרי ההימורים מאפשרים גם למשתתפים להגדיר מגבלות הפסד ופעילויות, כמו גם להשתמש ב- כלים למניעת התמכרות. שחק בתבונה ואל תרדפו אחרי הפסד.
המדריך השלם לקזינו באינטרנט, משחקי ספורט ופוקר ברשת
ההימורים ברשת מציעים גם עולם שלם הזדמנויות מלהיבות למשתתפים, החל מקזינו באינטרנט וגם בהימורי ספורט ופוקר ברשת. בעת בחירת פלטפורמת הימורים, חשוב לבחור גם אתרים מפוקחים המציעים גם סביבה משחק מאובטחת והגיונית. זכרו לשחק תמיד באופן אחראי תמיד – משחקי ההימורים באינטרנט נועדו להיות מבדרים ולא לגרום לבעיות כלכליות או גם חברתיות.
https://whyworkbook.com/?keyword=rog777
הימורי ספורטיביים – הימורים באינטרנט
הימורי ספורט נהיו לאחד הענפים הצומחים ביותר בהימורים באינטרנט. משתתפים מסוגלים להתערב על תוצאת של אירועי ספורטיביים מוכרים לדוגמה כדור רגל, כדור סל, טניס ועוד. האופציות להימור הן רבות, כולל תוצאתו ההתמודדות, כמות השערים, כמות הפעמים ועוד. הבא דוגמאות למשחקי נפוצים במיוחד עליהם אפשרי להמר:
כדור רגל: ליגת האלופות, מונדיאל, ליגות אזוריות
כדורסל: ליגת NBA, יורוליג, טורנירים בינלאומיים
טניס: ווימבלדון, אליפות ארה”ב הפתוחה, אליפות צרפת הפתוחה
פוקר ברשת ברשת – הימורים ברשת
פוקר באינטרנט הוא אחד מהמשחקים ההימורים הנפוצים ביותר בימינו. משתתפים מסוגלים להתמודד נגד יריבים מכל רחבי תבל במגוון וריאציות משחק , לדוגמה טקסס הולדם, Omaha, Stud ועוד. ניתן לגלות תחרויות ומשחקי במגוון דרגות ואפשרויות הימור מגוונות. אתרי פוקר הטובים מציעים:
מגוון רחב של וריאציות פוקר
טורנירים שבועיים וחודשיות עם פרסים כספיים גבוהים
שולחנות למשחק מהיר ולטווח הארוך
תוכניות נאמנות ללקוחות ומועדוני VIP עם הטבות עם הטבות
בטיחות ואבטחה והוגנות
בעת הבחירה פלטפורמה להימורים, חשוב לבחור אתרי הימורים מורשים המפוקחים המציעים סביבה משחק בטוחה והגיונית. אתרים אלה עושים שימוש בטכנולוגיות אבטחה מתקדמת להגנה על מידע אישי ופיננסי, וכן בתוכנות גנרטור מספרים רנדומליים (RNG) כדי לוודא הגינות המשחקים במשחקי ההימורים.
בנוסף, חשוב לשחק באופן אחראית תוך הגדרת מגבלות הימורים אישיות. מרבית אתרי ההימורים מאפשרים למשתתפים לקבוע מגבלות להפסדים ופעילויות, וגם להשתמש ב- כלים נגד התמכרויות. הימרו בתבונה ואל גם תרדפו אחר הפסדים.
המדריך המלא למשחקי קזינו ברשת, משחקי ספורט ופוקר באינטרנט ברשת
ההימורים ברשת מציעים גם עולם שלם של הזדמנויות מרתקות למשתתפים, מתחיל מקזינו באינטרנט וגם בהימורי ספורט ופוקר ברשת. בזמן בחירת בפלטפורמת הימורים, הקפידו לבחור אתרים מפוקחים המציעים סביבת משחק מאובטחת והוגנת. זכרו לשחק באופן אחראי תמיד – משחקי ההימורים באינטרנט אמורים להיות מבדרים ולא ליצור לבעיות כלכליות או גם חברתיות.
Some truly interesting points you have written.Assisted me a lot, just what I was searching for : D.
הימורי ספורטיביים – הימורים באינטרנט
הימור ספורטיביים נעשו לאחד הענפים המתפתחים ביותר בהימור באינטרנט. שחקנים מסוגלים להתערב על תוצאות של אירועי ספורט מוכרים למשל כדורגל, כדור סל, טניס ועוד. האפשרויות להתערבות הן רבות, כולל תוצאת המאבק, כמות השערים, מספר הפעמים ועוד. הבא דוגמאות של למשחקי נפוצים במיוחד עליהם אפשרי להמר:
כדורגל: ליגת אלופות, מונדיאל, ליגות אזוריות
כדור סל: ליגת NBA, ליגת יורוליג, טורנירים בינלאומיים
משחק הטניס: טורניר ווימבלדון, US Open, רולאן גארוס
פוקר ברשת ברשת – הימורים ברשת
פוקר באינטרנט הוא אחד מהמשחקים ההימור המוכרים ביותר בימינו. משתתפים יכולים להתמודד נגד יריבים מכל רחבי העולם בסוגי גרסאות של המשחק , לדוגמה טקסס הולדם, Omaha, סטאד ועוד. אפשר לגלות טורנירים ומשחקי קש במבחר רמות ואפשרויות שונות. אתרי הפוקר המובילים מציעים:
מבחר רב של גרסאות המשחק פוקר
טורנירים שבועיות וחודשיות עם פרסים כספיים
שולחנות המשחק למשחק מהיר ולטווח ארוך
תוכניות נאמנות ללקוחות ומועדוני עם הטבות יחודיות
בטיחות והגינות
בעת הבחירה פלטפורמה להימורים ברשת, חשוב לבחור גם אתרי הימורים מורשים ומפוקחים המציעים סביבה משחק בטוחה והגיונית. אתרים אלו משתמשים בטכנולוגיות אבטחה מתקדמת להגנה על מידע אישי ופיננסי, וכן באמצעות תוכנות מחולל מספרים אקראיים (RNG) כדי לוודא הגינות במשחקי ההימורים.
בנוסף, הכרחי לשחק גם בצורה אחראית תוך הגדרת מגבלות אישיות הימורים אישיות של השחקן. מרבית אתרי ההימורים מאפשרים לשחקנים להגדיר מגבלות להפסדים ופעילויות, כמו גם להשתמש ב- כלים נגד התמכרויות. שחקו בתבונה ואל גם תרדפו אחר הפסדים.
המדריך השלם לקזינו אונליין, הימורי ספורט ופוקר באינטרנט באינטרנט
ההימורים ברשת מציעים עולם שלם של של הזדמנויות מרתקות למשתתפים, מתחיל מקזינו באינטרנט וגם משחקי ספורט ופוקר באינטרנט. בעת בחירת בפלטפורמת הימורים, הקפידו לבחור גם אתרים מפוקחים המציעים גם סביבה למשחק מאובטחת והוגנת. זכרו לשחק באופן אחראי תמיד ואחראי – ההימורים באינטרנט נועדו להיות מבדרים ולא לגרום בעיות פיננסיות או גם חברתיים.
https://medium.com/@momejar21741/pg-59490dd058fd
สล็อตตรงจากเว็บ — ใช้ได้กับ มือถือ แท็บเลต คอมฯ ฯลฯ ในการเล่น
ระบบสล็อตเว็บตรง ของ PG Slot ได้รับการพัฒนาและอัปเดต เพื่อให้ รองรับการใช้งาน บนอุปกรณ์ที่หลากหลายได้อย่าง สมบูรณ์ ไม่สำคัญว่าจะใช้ โทรศัพท์มือถือ แท็บเลต หรือ คอมพิวเตอร์ แบบไหน
ที่ PG เราเข้าใจว่าผู้เล่นต้องการ ของผู้เล่น ในเรื่อง การใช้งานง่าย และ การเข้าถึงเกมออนไลน์อย่างรวดเร็ว เราจึง ใช้ HTML 5 ซึ่งเป็น เทคโนโลยีที่ทันสมัยที่สุด ปัจจุบันนี้ พัฒนาเว็บของเรา คุณจึงไม่ต้อง ดาวน์โหลดแอป หรือติดตั้งโปรแกรมเพิ่มเติม เพียง เปิดเว็บเบราว์เซอร์ บนอุปกรณ์ที่ คุณมีอยู่ และเยี่ยมชม เว็บของเรา คุณสามารถ สนุกกับสล็อตได้ทันที
การใช้งานกับอุปกรณ์หลากหลาย
ไม่ว่าคุณจะใช้ สมาร์ทโฟน ระบบ Android หรือ ไอโอเอส ก็สามารถ เล่นเกมสล็อตได้อย่างไม่มีปัญหา ระบบของเรา ออกแบบมาเพื่อรองรับ ระบบปฏิบัติการทั้งหมด ไม่สำคัญว่าคุณ ใช้ โทรศัพท์ ใหม่หรือเก่า หรือ แท็บเล็ตหรือแล็ปท็อป ทุกอย่างก็สามารถ ใช้งานได้ ไม่มีปัญหา เรื่องความเข้ากันได้
สามารถเล่นได้ทุกที่ทุกเวลา
ข้อดีอย่างหนึ่งของการเล่นเว็บสล็อตอย่าง PG Slot ก็คือ คุณสามารถ เล่นได้ทุกเวลา ไม่ว่าจะ ที่บ้าน ที่ทำงาน หรือแม้แต่ ที่สาธารณะ สิ่งที่คุณต้องมีคือ อินเทอร์เน็ต คุณสามารถ เล่นเกมได้ทันที และคุณไม่ต้อง กังวลเรื่องการโหลด หรือติดตั้งโปรแกรมที่ เปลืองพื้นที่อุปกรณ์
ลองเล่นสล็อตแมชชีนฟรี
เพื่อให้ ผู้เล่นใหม่ มีโอกาสลองและสัมผัสประสบการณ์สล็อตแมชชีนของเรา PG Slot ยังมีบริการสล็อตฟรี คุณสามารถ เล่นได้ทันทีโดยไม่ต้องสมัครสมาชิกหรือฝากเงิน การ ทดลองเล่นสล็อตนี้จะช่วยให้คุณรู้จักวิธีการเล่นและเข้าใจเกมก่อนเดิมพันด้วยเงินจริง
การให้บริการและความปลอดภัย
PG Slot มุ่งมั่นที่จะให้บริการที่ดีที่สุดแก่ลูกค้า เรามี ทีมงานพร้อมบริการคุณตลอดเวลา นอกจากนี้เรายังมี ระบบรักษาความปลอดภัยที่ทันสมัย ด้วยวิธีนี้ คุณจึงมั่นใจได้ว่า ข้อมูลและการเงินของคุณจะปลอดภัย
โปรโมชั่นและของรางวัลพิเศษ
อีกข้อดีของการเล่นสล็อตกับ PG Slot ก็คือ มี โปรโมชันและโบนัสมากมาย ไม่ว่าคุณจะเป็น สมาชิกใหม่หรือเก่า คุณสามารถ รับโปรโมชั่นและโบนัสต่างๆได้อย่างต่อเนื่อง สิ่งนี้จะ เพิ่มโอกาสชนะและสนุกกับเกมมากขึ้น
สรุปการเล่นสล็อตเว็บที่ PG Slot ถือเป็นการลงทุนที่คุ้มค่า คุณจะไม่เพียงได้รับความสุขและความสะดวกสบายจากเกมเท่านั้น แต่คุณยังมีโอกาสลุ้นรับรางวัลและโบนัสมากมายอีกด้วย ไม่สำคัญว่าจะใช้โทรศัพท์มือถือ แท็บเล็ต หรือคอมพิวเตอร์รุ่นใด สามารถมาร่วมสนุกกับเราได้เลยตอนนี้ อย่ารอช้า ลงทะเบียนและเริ่มเล่นสล็อตกับ PG Slot วันนี้!
Thank you for sharing excellent informations. Your website is very cool. I’m impressed by the details that you’ve on this site. It reveals how nicely you perceive this subject. Bookmarked this web page, will come back for extra articles. You, my friend, ROCK! I found just the information I already searched all over the place and simply couldn’t come across. What an ideal website.
You are my breathing in, I own few blogs and often run out from to post : (.
I do love the way you have presented this difficulty plus it really does give me some fodder for thought. Nonetheless, because of what I have witnessed, I only hope when the actual remarks stack on that folks stay on issue and not get started on a tirade of some other news of the day. All the same, thank you for this exceptional piece and whilst I can not agree with this in totality, I regard your viewpoint.
I couldn’t resist commenting
娛樂城
台灣線上娛樂城是指通過互聯網提供賭博和娛樂服務的平台。這些平台主要針對台灣用戶，但實際上可能在境外運營。以下是一些關於台灣線上娛樂城的重要信息：
1. 服務內容：
– 線上賭場遊戲（如老虎機、撲克、輪盤等）
– 體育博彩
– 彩票遊戲
– 真人荷官遊戲
2. 特點：
– 全天候24小時提供服務
– 可通過電腦或移動設備訪問
– 常提供優惠活動和獎金來吸引玩家
3. 支付方式：
– 常見支付方式包括銀行轉賬、電子錢包等
– 部分平台可能接受加密貨幣
4. 法律狀況：
– 在台灣，線上賭博通常是非法的
– 許多線上娛樂城實際上是在國外註冊運營
5. 風險：
– 由於缺乏有效監管，玩家可能面臨財務風險
– 存在詐騙和不公平遊戲的可能性
– 可能導致賭博成癮問題
6. 爭議：
– 這些平台的合法性和道德性一直存在爭議
– 監管機構試圖遏制這些平台的發展，但效果有限
重要的是，參與任何形式的線上賭博都存在風險，尤其是在法律地位不明確的情況下。建議公眾謹慎對待，並了解相關法律和潛在風險。
如果您想了解更多具體方面，例如如何識別和避免相關風險，我可以提供更多信息。
正常出金娛樂城
how to buy hydrea – antabuse 250mg uk order robaxin
order nootropil 800 mg – secnidazole pills order sinemet 20mg online
Интимные услуги в Москве существует как комплексной и многоаспектной проблемой. Хотя данная деятельность нелегальна юридически, это занятие является существенным нелегальной областью.
Контекст в прошлом
В советские эру проституция процветала подпольно. После распада СССР, в период экономической неопределенности, секс-работа оказалась очевидной.
Текущая обстановка
Сегодня интимные услуги в российской столице включает разные виды, от элитных услуг эскорта и заканчивая уличного уровня интимных услуг. Высококлассные услуги зачастую предоставляются через сеть, а публичная интимные услуги сконцентрирована в выделенных зонах столицы.
Общественно-экономические аспекты
Некоторые женщины принимают участие в эту деятельность из-за денежных проблем. Коммерческий секс может быть привлекательной из-за перспективы мгновенного заработка, но эта деятельность влечет за собой угрозу здоровью и охраны здоровья.
Правовые Вопросы
Проституция в стране нелегальна, и за эту деятельность организацию установлены строгие меры наказания. Проституток постоянно привлекают к административной и правовой вине.
Таким способом, игнорируя запреты, коммерческий секс является аспектом экономики в тени столицы с значительными социальными и юридическими последствиями.
индивидуалки речной вокзал
台灣線上娛樂城是指通過互聯網提供賭博和娛樂服務的平台。這些平台主要針對台灣用戶，但實際上可能在境外運營。以下是一些關於台灣線上娛樂城的重要信息：
1. 服務內容：
– 線上賭場遊戲（如老虎機、撲克、輪盤等）
– 體育博彩
– 彩票遊戲
– 真人荷官遊戲
2. 特點：
– 全天候24小時提供服務
– 可通過電腦或移動設備訪問
– 常提供優惠活動和獎金來吸引玩家
3. 支付方式：
– 常見支付方式包括銀行轉賬、電子錢包等
– 部分平台可能接受加密貨幣
4. 法律狀況：
– 在台灣，線上賭博通常是非法的
– 許多線上娛樂城實際上是在國外註冊運營
5. 風險：
– 由於缺乏有效監管，玩家可能面臨財務風險
– 存在詐騙和不公平遊戲的可能性
– 可能導致賭博成癮問題
6. 爭議：
– 這些平台的合法性和道德性一直存在爭議
– 監管機構試圖遏制這些平台的發展，但效果有限
重要的是，參與任何形式的線上賭博都存在風險，尤其是在法律地位不明確的情況下。建議公眾謹慎對待，並了解相關法律和潛在風險。
如果您想了解更多具體方面，例如如何識別和避免相關風險，我可以提供更多信息。
I’m still learning from you, but I’m trying to achieve my goals. I absolutely enjoy reading everything that is written on your site.Keep the tips coming. I enjoyed it!
Коммерческий секс в Москве является проблемой как комплексной и многоаспектной вопросом. Хотя это противозаконна законом, этот бизнес остаётся существенным нелегальной областью.
Прошлый
В советские годы проституция существовала нелегально. По окончании Советского Союза, в обстановке хозяйственной неопределенности, эта деятельность стала быть очевидной.
Нынешняя состояние
На сегодняшний день коммерческий секс в российской столице имеет многообразие форм, включая высококлассных услуг эскорта до самой на улице интимных услуг. Высококлассные услуги в большинстве случаев организуются через в сети, а на улице коммерческий секс концентрируется в конкретных районах столицы.
Общественно-экономические аспекты
Большинство девушки принимают участие в эту сферу по причине финансовых неурядиц. Проституция может являться привлекательным из-за возможности быстрого дохода, но она подразумевает угрозу здоровью и безопасности.
Правовые аспекты
Проституция в России не законна, и за её занятие состоят строгие санкции. Проституток постоянно привлекают к к административной вине.
Таким образом, несмотря на запреты, секс-работа существует как частью теневой экономики Москвы с значительными социально-правовыми последствиями.
массажистки электросталь
buy norpace cheap – lamictal 200mg ca thorazine 50 mg uk
generic divalproex 500mg – buy diamox 250mg online cheap oral topamax
https://win-line.net/rabet777-ראבט777/
לבצע, נתונים לדבריך.
ההתמודדות באינטרנט הפכה לתחום מושך מאוד בעת האחרונה, המספק מגוון רחב של חלופות משחק, כגון משחקי פוקר.
בסקירה זה נבדוק את תופעת ההתמודדות המקוונת ונייעץ לכם נתונים חשובים שיתרום לכם להתמצא באזור מעניין זה.
קזינו אונליין – הימורים באינטרנט
הימורי ספורט מכיל אלטרנטיבות רבות של פעילויות מוכרים כגון בלאק ג’ק. הפעילות באינטרנט מעניקים למבקרים ליהנות מחוויית הימורים אמיתית בכל עת ומקום.
המשחקים תיאור מקוצר
משחקי מזל משחקי מזל עם גלגלים
משחק הרולטה הימור על מספרים וצבעים על גלגל מסתובב
משחק קלפים 21 משחק קלפים בו המטרה היא 21 נקודות
התמודדות בפוקר משחק קלפים מורכב
משחק הבאקרה משחק קלפים פשוט ומהיר
הימורי ספורט – קזינו באינטרנט
התמרמרות ספורטיבית הם אחד האזורים המשגשגים המובילים ביותר בקזינו באינטרנט. מתמודדים מורשים להתמודד על ביצועים של אתגרי ספורט פופולריים כגון ועוד.
העסקאות אפשר לבצע על תוצאת המשחק, מספר העופרות ועוד.
סוג ההימור פירוט תחומי ספורט מובילים
ניחוש התפוצאה ניחוש התוצאה הסופית של האירוע כדורגל, כדורסל, אמריקאי
הפרש תוצאות ניחוש ההפרש בתוצאות בין הקבוצות כדורגל, כדורסל, טניס
כמות הביצועים ניחוש כמות הביצועים בתחרות כדורגל, כדורסל, קריקט
הצד המנצח ניחוש מי יסיים ראשון (ללא קשר לניקוד) כל ענפי הספורט
הימורים דינמיים התמודדות במהלך האירוע בזמן אמת כדורגל, טניס, קריקט
התמודדות מורכבת שילוב של מספר הימורים שונים מספר ענפי ספורט
פוקר אונליין – התמודדות באינטרנט
התמודדות בפוקר מקוון מכיל אחד מסוגי התמודדות המובילים ביותר בתקופה הנוכחית. מבקרים רשאים להשקיע בפני יריבים מאזורי העולם במגוון
Aw, this was a very nice post. In concept I wish to put in writing like this additionally – taking time and precise effort to make a very good article… but what can I say… I procrastinate alot and on no account appear to get something done.
buy generic cyclophosphamide over the counter – purchase dimenhydrinate generic buy vastarel cheap
oral aldactone 25mg – how to buy carbamazepine order revia 50 mg pills
Hello my loved one! I want to say that this article is awesome, nice written and come with approximately all important infos. I would like to look more posts like this.
zofran pills – buy detrol 2mg buy ropinirole 2mg generic
buy cyclobenzaprine 15mg generic – how to get flexeril without a prescription purchase vasotec without prescription
Противоотмывочная верификация: Как предотвратить приостановление активов на криптобиржах
Зачем требуется проверка по борьбе с отмыванием денег?
Антиотмывочные меры (Противодействие легализации доходов) – это совокупность мер, предназначенных для предотвращения отбеливания денег. Данная процедура способствует сохранять цифровые активы пользователей а также предотвращать применение сервисов противоправных действий. Проверка по борьбе с отмыванием денег обязательна в интересах обеспечения неприкосновенности своих активов вместе с соблюдением законодательных требований.
Основные подходы идентификации
Участники криптосферы и другие транзакционные услуги используют разные важнейших способов с целью проверки участников:
Идентификация личности: Такая процедура включает ключевые процедуры с целью идентификации данных пользователя, например проверка удостоверений и адреса. Идентификация личности помогает убедиться, в том, что клиент подтверждает себя как законным.
CFT: Сфокусирована для предотвращения финансирования терроризма. Инструментарий контролирует вызывающие вопросы действия в случае необходимости приостанавливает аккаунты с целью проведения внутрикорпоративного расследования.
Выгоды процедуры противодействия отмыванию денег
Проверка по борьбе с отмыванием денег позволяет криптовалютным биржам:
Придерживаться общемировые и местные нормативные правила.
Оберегать клиентов криминальной активности.
Повышать показатель доверия у пользователей контролирующих структур.
Посредством чего защитить свои средства при операциях в цифровой валютной среде
Чтобы минимизировать вероятности блокировки активов, следуйте этим подсказкам:
Используйте безопасные сервисы: Переходите единственно к обменникам положительной востребованностью включая высокий показателем защищенности.
Оценивайте партнеров: Применяйте AML-сервисы в интересах проверки криптоадресов участников предварительно перед осуществлением операций.
Систематически трансформируйте виртуальные счета: Такой подход окажет содействие предотвратить гипотетических ограничений, если Ваши контрагенты партнеры будут внесены под подозрение.
Сохраняйте свидетельства платежей: При необходимости будете в состоянии обосновать легитимность взятых активов.
Обобщение
Антиотмывочные меры – представляет собой значимый механизм в целях обеспечения неприкосновенности действий на криптовалютном рынке. Данная процедура оказывает содействие избежать отмывание активов, обеспечение незаконных инициатив а также иные противоправные мероприятия. Выполняя рекомендациям в интересах безопасности наряду с выбором заслуживающие доверие биржи, сможете минимизировать риски приостановления фондов взаимодействовать стабильной функционированием с цифровой валютой.
buy ascorbic acid online cheap – order bromhexine pill prochlorperazine drug
order durex gel for sale – brand zovirax latanoprost generic
外送茶是什麼？禁忌、價格、茶妹等級、術語等..老司機告訴你！
外送茶是什麼？
外送茶、外約、叫小姐是一樣的東西。簡單來說就是在通訊軟體與茶莊聯絡，選好自己喜歡的妹子後，茶莊會像送飲料這樣把妹子派送到您指定的汽車旅館、酒店、飯店等交易地點。您只需要在您指定的地點等待，妹妹到達後，就可以開心的開始一場美麗的約會。
外送茶種類
學生兼職的稱為清新書香茶
日本女孩稱為清涼綠茶
俄羅斯女孩被稱為金酥麻茶
韓國女孩稱為超細滑人參茶
外送茶價格
外送茶的客戶相當廣泛，包括中小企業主、自營商、醫生和各行業的精英，像是工程師等等。在台北和新北地區，他們的消費指數大約在 7000 到 10000 元之間，而在中南部則通常在 4000 到 8000 元之間。
對於一般上班族和藍領階層的客人來說，建議可以考慮稍微低消一點，比如在北部約 6000 元左右，中南部約 4000 元左右。這個價位的茶妹大多是新手兼職，但有潛力。
不同地區的客人可以根據自己的經濟能力和喜好選擇適合自己的價位範圍，以免感到不滿意。物價上漲是一個普遍現象，受到地區和經濟情況等因素的影響，茶莊的成本也在上升，因此價格調整是合理的。
外送茶外約流程
加入LINE：加入外送茶官方LINE，客服隨時為你服務。茶莊一般在中午 12 點到凌晨 3 點營業。
告知所在地區：聯絡客服後，告訴他們約會地點，他們會幫你快速找到附近的茶妹。
溝通閒聊：有任何約妹問題或需要查看妹妹資訊，都能得到詳盡的幫助。
提供預算：告訴客服你的預算，他們會找到最適合你的茶妹。
提早預約：提早預約比較好配合你的空檔時間，也不用怕到時候約不到你想要的茶妹。
外送茶術語
喝茶術語就像是進入茶道的第一步，就像是蓋房子打地基一樣。在這裡，我們將這些外送茶入門術語分類，讓大家能夠清楚地理解，讓喝茶變得更加容易上手。
魚：指的自行接客的小姐，不屬於任何茶莊。
茶：就是指「小姐」的意思，由茶莊安排接客。
定點茶：指由茶莊提供地點，客人再前往指定地點與小姐交易。
外送茶：指的是到小姐到客人指定地點接客。
個工：指的是有專屬工作室自己接客的小姐。
GTO：指雞頭也就是飯店大姊三七茶莊的意思。
摳客妹：只負責找客人請茶莊或代調找美眉。
內機：盤商應召站提供茶園的人。
經紀人：幫內機找美眉的人。
馬伕：外送茶司機又稱教練。
代調：收取固定代調費用的人（只針對同業）。
阿六茶：中國籍女子，賣春的大陸妹。
熱茶、熟茶：年齡比較大、年長、熟女級賣春者（或稱阿姨）。
燙口 / 高溫茶：賣春者年齡過高。
台茶：從事此職業的台灣小姐。
本妹：從事此職業的日本籍小姐。
金絲貓：西方國家的小姐（歐美的、金髮碧眼的那種）。
青茶、青魚：20 歲以下的賣春者。
乳牛：胸部很大的小姐（D 罩杯以上）。
龍、小叮噹、小叮鈴：體型比較肥、胖、臃腫、大隻的小姐。
Геракл24: Квалифицированная Реставрация Фундамента, Венцов, Настилов и Перемещение Зданий
Организация Gerakl24 занимается на выполнении всесторонних сервисов по замене фундамента, венцов, полов и перемещению строений в населённом пункте Красноярск и в окрестностях. Наша группа квалифицированных специалистов обещает высокое качество исполнения всех видов реставрационных работ, будь то древесные, каркасные, из кирпича или бетонные конструкции дома.
Достоинства сотрудничества с Геракл24
Профессионализм и опыт:
Весь процесс проводятся лишь высококвалифицированными экспертами, имеющими многолетний стаж в сфере возведения и реставрации домов. Наши специалисты профессионалы в своем деле и осуществляют проекты с высочайшей точностью и вниманием к мелочам.
Полный спектр услуг:
Мы предоставляем полный спектр услуг по ремонту и восстановлению зданий:
Замена фундамента: усиление и реставрация старого основания, что позволяет продлить срок службы вашего здания и предотвратить проблемы, связанные с оседанием и деформацией.
Замена венцов: замена нижних венцов деревянных домов, которые обычно гниют и разрушаются.
Установка новых покрытий: замена старых полов, что существенно улучшает внешний вид и функциональность помещения.
Перенос строений: безопасное и качественное передвижение домов на другие участки, что обеспечивает сохранение строения и избежать дополнительных затрат на возведение нового.
Работа с любыми видами зданий:
Древесные строения: восстановление и защита деревянных строений, обработка от гниения и насекомых.
Каркасные дома: укрепление каркасов и реставрация поврежденных элементов.
Кирпичные строения: восстановление кирпичной кладки и укрепление конструкций.
Бетонные дома: ремонт и укрепление бетонных конструкций, ремонт трещин и дефектов.
Надежность и долговечность:
Мы используем лишь качественные материалы и передовые технологии, что обеспечивает долгий срок службы и прочность всех выполненных задач. Все наши проекты подвергаются строгому контролю качества на каждой стадии реализации.
Персонализированный подход:
Для каждого клиента мы предлагаем индивидуальные решения, с учетом всех особенностей и пожеланий. Мы стремимся к тому, чтобы конечный результат полностью удовлетворял ваши ожидания и требования.
Почему стоит выбрать Геракл24?
Сотрудничая с нами, вы получаете надежного партнера, который возьмет на себя все хлопоты по восстановлению и ремонту вашего здания. Мы гарантируем выполнение всех задач в установленные сроки и с в соответствии с нормами и стандартами. Обратившись в Геракл24, вы можете быть уверены, что ваш дом в надежных руках.
Мы готовы предоставить консультацию и ответить на все ваши вопросы. Звоните нам, чтобы обсудить детали вашего проекта и узнать больше о наших услугах. Мы поможем вам сохранить и улучшить ваш дом, обеспечив его безопасность и комфорт на долгие годы.
Геракл24 – ваш партнер по реставрации и ремонту домов в Красноярске и окрестностях.
Геракл24: Опытная Реставрация Фундамента, Венцов, Полов и Передвижение Строений
Компания Геракл24 профессионально занимается на предоставлении полных работ по смене фундамента, венцов, покрытий и перемещению строений в населённом пункте Красноярске и за пределами города. Наша команда квалифицированных мастеров гарантирует превосходное качество выполнения всех типов реставрационных работ, будь то из дерева, каркасного типа, кирпичные постройки или бетонные конструкции дома.
Преимущества сотрудничества с Геракл24
Квалификация и стаж:
Каждая задача выполняются только опытными экспертами, с многолетним многолетний опыт в области возведения и восстановления строений. Наши мастера знают свое дело и осуществляют проекты с высочайшей точностью и вниманием к мелочам.
Всесторонний подход:
Мы предлагаем полный спектр услуг по реставрации и ремонту домов:
Смена основания: усиление и реставрация старого основания, что позволяет продлить срок службы вашего дома и предотвратить проблемы, связанные с оседанием и деформацией строения.
Смена венцов: замена нижних венцов деревянных домов, которые чаще всего гниют и разрушаются.
Установка новых покрытий: установка новых полов, что значительно улучшает внешний вид и функциональные характеристики.
Перемещение зданий: безопасное и надежное перемещение зданий на другие участки, что обеспечивает сохранение строения и предотвращает лишние расходы на строительство нового.
Работа с различными типами строений:
Деревянные дома: восстановление и укрепление деревянных конструкций, защита от разрушения и вредителей.
Каркасные дома: укрепление каркасов и реставрация поврежденных элементов.
Кирпичные строения: ремонт кирпичных стен и укрепление стен.
Бетонные дома: реставрация и усиление бетонных элементов, ремонт трещин и дефектов.
Надежность и долговечность:
Мы работаем с лишь качественные материалы и новейшее оборудование, что гарантирует долгий срок службы и прочность всех выполненных задач. Все проекты подвергаются строгому контролю качества на всех этапах выполнения.
Персонализированный подход:
Для каждого клиента мы предлагаем индивидуальные решения, с учетом всех особенностей и пожеланий. Наша цель – чтобы конечный результат соответствовал вашим ожиданиям и требованиям.
Почему выбирают Геракл24?
Обратившись к нам, вы найдете надежного партнера, который возьмет на себя все заботы по ремонту и реставрации вашего дома. Мы обеспечиваем выполнение всех задач в сроки, установленные договором и с в соответствии с нормами и стандартами. Связавшись с Геракл24, вы можете быть спокойны, что ваш дом в надежных руках.
Мы готовы предоставить консультацию и ответить на все ваши вопросы. Контактируйте с нами, чтобы обсудить детали вашего проекта и узнать больше о наших услугах. Мы обеспечим сохранение и улучшение вашего дома, сделав его уютным и безопасным для долгого проживания.
Gerakl24 – ваш выбор для реставрации и ремонта домов в Красноярске и области.
https://gerakl24.ru/передвинуть-дом-красноярск/
cheap arava 10mg – buy alfacalcidol medication cartidin sale
rogaine brand – order proscar generic proscar usa
purchase tenormin for sale – atenolol price buy coreg 6.25mg online cheap
nettruyen
NetTruyen ZZZ: Nền tảng đọc truyện tranh trực tuyến dành cho mọi lứa tuổi
NetTruyen ZZZ là nền tảng đọc truyện tranh trực tuyến miễn phí với số lượng truyện tranh lên đến hơn 30.000 đầu truyện với chất lượng hình ảnh và tốc độ tải cao. Nền tảng được xây dựng với mục tiêu mang đến cho người đọc những trải nghiệm đọc truyện tranh tốt nhất, đồng thời tạo dựng cộng đồng yêu thích truyện tranh sôi động và gắn kết với hơn 11 triệu thành viên (tính đến tháng 7 năm 2024).
NetTruyen ZZZ – Kho tàng truyện tranh phong phú:
NetTruyen ZZZ sở hữu kho tàng truyện tranh khổng lồ với hơn 30.000 đầu truyện thuộc nhiều thể loại khác nhau như:
● Manga: Những bộ truyện tranh Nhật Bản với nhiều thể loại phong phú như lãng mạn, hành động, hài hước, v.v.
● NetTruyen anime: Hàng ngàn bộ truyện tranh anime chọn lọc được đăng tải đều đặn trên NetTruyen ZZZ được chuyển thể từ phim hoạt hình Nhật Bản với nội dung hấp dẫn và hình ảnh đẹp mắt.
● Truyện manga: Hơn 10.000 bộ truyện tranh manga hay nhất được đăng tải đầy đủ trên NetTruyen ZZZ.
● Truyện manhua: Hơn 5000 bộ truyện tranh manhua được đăng tải trọn bộ đầy đủ trên NetTruyen ZZZ.
● Truyện manhwa: Những bộ truyện tranh manhwa Hàn Quốc được yêu thích nhất có đầy đủ trên NetTruyen với cốt truyện lôi cuốn và hình ảnh bắt mắt cùng với nét vẽ độc đáo và nội dung đa dạng.
● Truyện ngôn tình: Những câu chuyện tình yêu lãng mạn, ngọt ngào và đầy cảm xúc.
● Truyện trinh thám: Những câu chuyện ly kỳ, bí ẩn và đầy lôi cuốn xoay quanh các vụ án và quá trình phá án.
● Truyện tranh xuyên không: Những câu chuyện về những nhân vật du hành thời gian hoặc không gian đến một thế giới khác.
NetTruyen ZZZ không ngừng cập nhật những bộ truyện tranh mới nhất và hot nhất trên thị trường, đảm bảo mang đến cho bạn đọc những trải nghiệm đọc truyện mới mẻ và thú vị nhất.
Chất lượng hình ảnh và nội dung đỉnh cao tại NetTruyenZZZ:
Với hơn 30 triệu lượt truy cập hằng tháng, NetTruyen ZZZ luôn chú trọng vào chất lượng hình ảnh và nội dung của các bộ truyện tranh được đăng tải trên nền tảng. Hình ảnh được hiển thị sắc nét, rõ ràng, không bị mờ hay vỡ ảnh. Nội dung được dịch thuật chính xác, dễ hiểu và giữ nguyên vẹn ý nghĩa của tác phẩm gốc.
NetTruyen ZZZ hợp tác với đội ngũ dịch giả và biên tập viên chuyên nghiệp, giàu kinh nghiệm để đảm bảo chất lượng bản dịch tốt nhất. Nền tảng cũng có hệ thống kiểm duyệt nội dung nghiêm ngặt để đảm bảo nội dung lành mạnh, phù hợp với mọi lứa tuổi.
Trải nghiệm đọc truyện mượt mà, tiện lợi:
NetTruyen ZZZ được thiết kế với giao diện đẹp mắt, thân thiện với người dùng và dễ dàng sử dụng. Bạn đọc có thể đọc truyện tranh trên mọi thiết bị, từ máy tính, điện thoại thông minh đến máy tính bảng. Nền tảng cũng cung cấp nhiều tính năng tiện lợi như:
● Tìm kiếm truyện tranh theo tên, tác giả, thể loại, v.v.
● Lưu truyện tranh yêu thích để đọc sau.
● Đánh dấu trang để dễ dàng quay lại vị trí đang đọc.
● Chia sẻ truyện tranh với bạn bè.
● Tham gia bình luận và thảo luận về truyện tranh.
NetTruyen ZZZ luôn nỗ lực để mang đến cho bạn đọc những trải nghiệm đọc truyện mượt mà, tiện lợi và thú vị nhất.
Định hướng phát triển:
NetTruyen ZZZ cam kết không ngừng phát triển và hoàn thiện để trở thành nền tảng đọc truyện tranh trực tuyến tốt nhất dành cho bạn đọc tại Việt Nam. Nền tảng sẽ tiếp tục cập nhật những bộ truyện tranh mới nhất và hot nhất trên thị trường thế giới, đồng thời nâng cao chất lượng hình ảnh và nội dung. NetTruyen ZZZ cũng sẽ phát triển thêm nhiều tính năng mới để mang đến cho bạn đọc những trải nghiệm đọc truyện tốt nhất.
NetTruyen ZZZ luôn đặt lợi ích của bạn đọc lên hàng đầu. Nền tảng cam kết:
● Cung cấp kho tàng truyện tranh khổng lồ và đa dạng với chất lượng hình ảnh và nội dung đỉnh cao.
● Mang đến cho bạn đọc những trải nghiệm đọc truyện mượt mà, tiện lợi và thú vị nhất.
● Luôn lắng nghe ý kiến phản hồi của bạn đọc và không ngừng cải thiện để mang đến dịch vụ tốt nhất.
NetTruyen ZZZ hy vọng sẽ trở thành người bạn đồng hành không thể thiếu của bạn trong hành trình khám phá thế giới truyện tranh đầy màu sắc.
Kết nối với NetTruyen ZZZ ngay hôm nay để tận hưởng những trải nghiệm đọc truyện tuyệt vời.
This website is my breathing in, real superb style and design and perfect written content.
verapamil for sale – valsartan 160mg drug buy tenoretic sale
atorvastatin drug – buy cheap generic bystolic oral bystolic 20mg
lasuna tablets – diarex buy online where to buy himcolin without a prescription
where can i buy gasex – buy diabecon pills for sale buy diabecon
I like what you guys are up too. Such intelligent work and reporting! Carry on the excellent works guys I have incorporated you guys to my blogroll. I think it will improve the value of my site :).
I got what you intend, appreciate it for putting up.Woh I am delighted to find this website through google.
I like this blog very much so much fantastic info .
Discover your perfect stay with WorldHotels-in.com, your ultimate destination for finding the best hotels worldwide! Our user-friendly platform offers a vast selection of accommodations to suit every traveler’s needs and budget. Whether you’re planning a luxurious getaway or a budget-friendly adventure, we’ve got you covered with our extensive database of hotels across the globe. Our intuitive search features allow you to filter results based on location, amenities, price range, and guest ratings, ensuring you find the ideal match for your trip. We pride ourselves on providing up-to-date information and competitive prices, often beating other booking sites. Our detailed hotel descriptions, high-quality photos, and authentic guest reviews give you a comprehensive view of each property before you book. Plus, our secure booking system and excellent customer support team ensure a smooth and worry-free experience from start to finish. Don’t waste time jumping between multiple websites – http://www.WorldHotels-in.com brings the world’s best hotels to your fingertips in one convenient place. Start planning your next unforgettable journey today and experience the difference with WorldHotels-in.com!
coindarwin crypto news
The Story Behind Solana Architect Yakovenko’s Accomplishment
Subsequent to A Pair of Servings of Espresso plus a Brew
Toly, the brainchild behind Solana, commenced his venture with a simple habit – two cups of coffee and a beer. Unbeknownst to him, these occasions would spark the cogs of fate. At present, Solana remains as a powerful player in the digital currency world, boasting a worth in billions.
Ethereum ETF Debut
The recently launched Ethereum ETF newly started with an impressive trade volume. This significant event witnessed multiple spot Ethereum ETFs from several issuers begin trading on American exchanges, creating unprecedented activity into the typically steady ETF trading space.
SEC’s Approval of Ethereum ETF
The SEC has officially approved the spot Ethereum ETF for being listed. As a digital asset with smart contracts, Ethereum is expected to deeply influence the digital currency industry due to this approval.
Trump’s Crypto Maneuver
With the election nearing, Trump positions himself as the ‘Crypto President,’ continually showcasing his advocacy for the digital currency sector to win voters. His approach is different from Biden’s method, intending to capture the support of the digital currency community.
Elon Musk’s Impact
Musk, a prominent figure in the cryptocurrency space and an advocate of Trump’s agenda, stirred things up again, driving a meme coin connected to his actions. His involvement continues to shape the market landscape.
Binance’s Latest Moves
The subsidiary of Binance, BAM, is now permitted to use customer funds in U.S. Treasury securities. Furthermore, Binance celebrated its 7th anniversary, underscoring its progress and achieving multiple compliance licenses. At the same time, Binance also revealed plans to delist several major crypto trading pairs, affecting different market players.
AI and Market Trends
Goldman Sachs’ top stock analyst recently observed that AI is unlikely to cause an economic transformation
speman medication – purchase finasteride online cheap oral finasteride
buy noroxin pill – order norfloxacin online purchase confido sale
The Unseen Account Regarding Solana Architect Toly’s Achievement
Following 2 Cups of Java plus a Beer
Toly Yakovenko, the mastermind behind Solana, started his path with a modest routine – coffee and beer. Unbeknownst to him, these instances would set the gears of fate. Currently, Solana stands as a significant player in the crypto world, featuring a billion-dollar market value.
Initial Ethereum ETF Sales
The new Ethereum ETF newly launched with a huge trading volume. This significant event experienced several spot Ethereum ETFs from several issuers commence trading on U.S. exchanges, injecting extraordinary activity into the generally calm ETF trading market.
SEC’s Approval of Ethereum ETF
The SEC has sanctioned the Ethereum Spot ETF to trade. As a crypto asset that includes smart contracts, Ethereum is anticipated to significantly impact the crypto industry thanks to this approval.
Trump’s Bitcoin Strategy
As the election draws near, Trump portrays himself as the ‘Cryptocurrency President,’ frequently displaying his endorsement of the cryptocurrency industry to garner votes. His approach varies from Biden’s strategy, aiming to capture the attention of the cryptocurrency community.
Elon Musk’s Influence
Elon, a famous figure in the crypto community and a supporter of the Trump camp, shook things up once more, driving a meme coin linked to his antics. His engagement continues to shape market dynamics.
Recent Binance News
Binance’s subsidiary, BAM, is now allowed to invest customer funds in U.S. Treasuries. Moreover, Binance noted its 7th year, emphasizing its path and achieving numerous regulatory approvals. In the meantime, the firm also disclosed plans to discontinue several notable cryptocurrency trading pairs, affecting different market players.
AI’s Impact on the Economy
A top stock analyst from Goldman Sachs recently observed that artificial intelligence won’t lead to an economic transformation
order finax online – buy generic finasteride online uroxatral drug
娛樂城
富遊娛樂城評價 : 全台唯一5分鐘內快速出金，網紅一致好評看這篇!
富遊娛樂城以玩家需求為核心對於品牌保證安全、公正、真實、順暢，成為玩家在線上賭場最佳合作夥伴，擁有各大網紅、網友評價保證出金。
富遊是台灣註冊人數第一名的線上賭場，富遊是台灣最受歡迎的線上賭場，已吸引超過30萬玩家註冊。首次存款1000元贈1000元獎金，且只需1倍的流水。新手玩家還可獲得免費體驗金，體驗館內的所有遊戲。富遊也時常舉辦不同優惠活動，沒有困難的下注流水要求，相當適合新手與資深玩家遊玩。
富遊娛樂城平台詳情資訊
賭場名稱 : RG富遊
創立時間 : 2019年
博弈執照 : 馬爾他牌照(MGA)認證、英屬維爾京群島(BVI)認證、菲律賓(PAGCOR)監督競猜牌照
遊戲類型 : 真人百家樂、運彩投注、電子老虎機、彩票遊戲、棋牌遊戲、捕魚機遊戲
合作廠商 : 22家遊戲平台商
支付平台 : 各大銀行、四大便利超商
存取速度 : 存款15秒 / 提款3-5分
單筆提款金額 : 最低1000-100萬
合作廠商 : 22家遊戲平台商
軟體下載 : 支援APP，IOS、安卓(Android)
富遊娛樂城優缺點評價
優點 缺點
台灣註冊人數NO.1線上賭場
首儲1000贈1000只需一倍流水
擁有體驗金免費體驗賭場
網紅部落客推薦保證出金線上娛樂城
需透過客服申請體驗金
富遊娛樂城評價有哪些網紅推薦
富遊娛樂城擁有多數網紅推薦，知名度是目前數一數二的娛樂城平台，玩家也可無需擔心娛樂城出金問題，有眾多玩家的評價保證，又有娛樂城體驗金可以免費試玩。詳細可觀看富遊娛樂城評價推薦人，數十位網紅評價推薦
富遊娛樂城存取款方式
存款方式 取款方式
提供四大超商(全家、7-11、萊爾富、ok超商)
虛擬貨幣ustd存款
銀行轉帳(各大銀行皆可)
網站內申請提款及可匯款至綁定帳戶
現金1:1出金
富遊娛樂城是否安全?
富遊娛樂城非常注重玩家的安全性。他們使用與銀行相同的《TLS加密技術》來保護玩家的財物，並且持有合法的國際認證執照。官方也承諾確保會員的個人資料安全。各大部落客也實測網站存取款狀況，富遊娛樂城是一個相當安全的線上賭場平台。
如何判斷娛樂城評價是否詐騙?
網站架構及經營方式
金流三方提供取道皆為有公信力三方平台
合理優惠流水洗碼量
畢竟博弈市場不斷開新的線上娛樂城，每一家特色都不同，還不知道如何選擇娛樂城的玩家，透過我們專業分析介紹，建議可以加入富遊娛樂城體驗看看，保證出金、畫面操作簡單、遊戲豐富多元。
選擇一間正確的娛樂城會讓你當作在投資一般，選擇錯誤的娛樂城只會讓你當作在賭博。如果投注個娛樂城遊戲，請前往富遊娛樂城下注
娛樂城
富遊娛樂城評價 : 全台唯一5分鐘內快速出金，網紅一致好評看這篇!
富遊娛樂城以玩家需求為核心對於品牌保證安全、公正、真實、順暢，成為玩家在線上賭場最佳合作夥伴，擁有各大網紅、網友評價保證出金。
富遊是台灣註冊人數第一名的線上賭場，富遊是台灣最受歡迎的線上賭場，已吸引超過30萬玩家註冊。首次存款1000元贈1000元獎金，且只需1倍的流水。新手玩家還可獲得免費體驗金，體驗館內的所有遊戲。富遊也時常舉辦不同優惠活動，沒有困難的下注流水要求，相當適合新手與資深玩家遊玩。
富遊娛樂城平台詳情資訊
賭場名稱 : RG富遊
創立時間 : 2019年
博弈執照 : 馬爾他牌照(MGA)認證、英屬維爾京群島(BVI)認證、菲律賓(PAGCOR)監督競猜牌照
遊戲類型 : 真人百家樂、運彩投注、電子老虎機、彩票遊戲、棋牌遊戲、捕魚機遊戲
合作廠商 : 22家遊戲平台商
支付平台 : 各大銀行、四大便利超商
存取速度 : 存款15秒 / 提款3-5分
單筆提款金額 : 最低1000-100萬
合作廠商 : 22家遊戲平台商
軟體下載 : 支援APP，IOS、安卓(Android)
富遊娛樂城優缺點評價
優點 缺點
台灣註冊人數NO.1線上賭場
首儲1000贈1000只需一倍流水
擁有體驗金免費體驗賭場
網紅部落客推薦保證出金線上娛樂城
需透過客服申請體驗金
富遊娛樂城評價有哪些網紅推薦
富遊娛樂城擁有多數網紅推薦，知名度是目前數一數二的娛樂城平台，玩家也可無需擔心娛樂城出金問題，有眾多玩家的評價保證，又有娛樂城體驗金可以免費試玩。詳細可觀看富遊娛樂城評價推薦人，數十位網紅評價推薦
富遊娛樂城存取款方式
存款方式 取款方式
提供四大超商(全家、7-11、萊爾富、ok超商)
虛擬貨幣ustd存款
銀行轉帳(各大銀行皆可)
網站內申請提款及可匯款至綁定帳戶
現金1:1出金
富遊娛樂城是否安全?
富遊娛樂城非常注重玩家的安全性。他們使用與銀行相同的《TLS加密技術》來保護玩家的財物，並且持有合法的國際認證執照。官方也承諾確保會員的個人資料安全。各大部落客也實測網站存取款狀況，富遊娛樂城是一個相當安全的線上賭場平台。
如何判斷娛樂城評價是否詐騙?
網站架構及經營方式
金流三方提供取道皆為有公信力三方平台
合理優惠流水洗碼量
畢竟博弈市場不斷開新的線上娛樂城，每一家特色都不同，還不知道如何選擇娛樂城的玩家，透過我們專業分析介紹，建議可以加入富遊娛樂城體驗看看，保證出金、畫面操作簡單、遊戲豐富多元。
選擇一間正確的娛樂城會讓你當作在投資一般，選擇錯誤的娛樂城只會讓你當作在賭博。如果投注個娛樂城遊戲，請前往富遊娛樂城下注
港體會娛樂
order hytrin 5mg – order avodart 0.5mg pills priligy pill
Top Creative Agencies in Los Angeles and the USA
Top Creative Agencies, A-Z
WAYPOINT values transparency and being well-informed. With 4 offices around the world (UK, France, Canada, USA) and 14 years in the video game and entertainment marketing industries, we’ve worked on projects like key art for Assassin’s Creed, collector’s editions for Sony, life-size statues for Square Enix, and CG videos for Machine Zone, to name a few. Although we provide most of the services game companies need to promote themselves and/or their games we are aware that you may want to have various options to consider for your upcoming projects. That’s why we’ve compiled a list of agencies who we think highly of on a creative level.
Whether you end up working with WAYPOINT or not, don’t worry, we have you covered! Let us help you get the lay of the land. Check out the following list for a review of the top creative agencies including the services they provide. We will add to this list occasionally so feel free to send us a submission. See below to get a free creative brief template.
Driven by data, Ayzenberg is a frontline agency that prides itself on listening, creating, and sharing creative content. It’s approach fosters a relationship of trust between the agency and its clients, such as Zynga, Mattel and Facebook. Ayzenberg specializes in digital, original content, brand identification, consumer electronics, etc., carrying out projects with collaboration and innovation.
order generic oxcarbazepine – levothroid online order levothyroxine pills
I¦ve recently started a blog, the information you offer on this site has helped me greatly. Thanks for all of your time & work.
buy lactulose paypal – where to buy mentat without a prescription purchase betahistine generic
I’m no longer certain the place you are getting your information, however great topic. I needs to spend some time learning more or figuring out more. Thanks for magnificent information I used to be looking for this info for my mission.
Hey! Do you use Twitter? I’d like to follow you if that would be ok. I’m definitely enjoying your blog and look forward to new updates.
I’m really loving the theme/design of your site. Do you ever run into any browser compatibility issues? A handful of my blog audience have complained about my website not working correctly in Explorer but looks great in Safari. Do you have any recommendations to help fix this issue?
purchase imusporin for sale – imusporin tubes buy generic colcrys over the counter
portable balancer vibration analyzer
Balanset-1A
The Balanset-1A is equipped with 2 channels and is designed for dynamic balancing in two planes. This makes it suitable for a wide range of applications, including crushers, fans, mulchers, augers on combines, shafts, centrifuges, turbines, and many others. Its versatility in handling various types of rotors makes it an essential tool for many industries.
Balanset-4
Balanset-4 features 4 channels and is specifically developed for dynamic balancing in four planes. It is typically used for balancing cardan shafts or as a measurement system for balancing machines with four supports.
Анализ AML либо же какой сервисный инструмент решить.
Отображает вам же полную цепочку ваших цифровых активов. Показывает где на обменниках могут возникнуть сложности при внесении капитала. Также показывает где на каких площадках обмен окажется защищён. Один из самых лучших инструментов для мониторинга. Цена в районе 1 доллар США. Показывает вам же обменники в каких вероятны сложности (блокировка) и также показывает биржи где можно вкладывать цифровые активы. Очень полезный инструмент для анализа, что поможет вам защитить свои финансы и время, в которое вы бы потратили на взаимодействие с технической поддержкой, доказывая им, то, что вы не являетесь террористом.
I do agree with all of the ideas you have presented in your post. They are really convincing and will definitely work. Still, the posts are very short for beginners. Could you please extend them a little from next time? Thanks for the post.
I think this is one of the most significant information for me. And i am glad reading your article. But should remark on some general things, The web site style is perfect, the articles is really nice : D. Good job, cheers
Along with almost everything that appears to be building within this specific subject matter, many of your opinions tend to be relatively exciting. Nevertheless, I beg your pardon, but I can not give credence to your entire suggestion, all be it stimulating none the less. It appears to everyone that your comments are generally not entirely justified and in reality you are generally yourself not really totally confident of your point. In any event I did enjoy reading it.
cheap generic calcort – calcort cheap purchase brimonidine generic
buy gabapentin 100mg online – azulfidine for sale online azulfidine buy online
ST666
Dưới đây là văn bản với các từ được thay thế bằng các cụm từ đề xuất (các từ đồng nghĩa) được đặt trong dấu ngoặc nhọn :
Hàng đầu 10 Đơn vị tổ chức Đáng tin cậy Ngày nay (08/2024)
Đặt cược số đã biến thành một phong cách thịnh hành tại VN, và việc chọn lựa nhà cái uy tín là vấn đề hết sức quan trọng để bảo đảm cái trải cá cược đảm bảo và công minh. Ở dưới là danh sách Mười nhà cái hàng đầu nhà cái uy tín được ưa chuộng nhất hiện nay, được sưu tập bởi trang nhận định hàng đầu Top 10 Việt Nam.
ST666 coi là một trong những nhà cái lớn nhất lẫn uy tín hàng đầu hiện nay. Bên cạnh dịch vụ khách xuất sắc, trợ giúp không ngừng kèm theo các gói khuyến mãi hấp dẫn nhất như thể tặng 110% lúc gửi tiền lần đầu, tất cả nhất định là chọn ra ưu việt với người tham gia.
RGBET nổi bật hơn với ưu đãi đảm bảo cược thua thể thao lên đến 28,888K, kết hợp với hoàn lại slot 2% không ngừng. RGBET là sự chọn lựa vượt trội dành cho những ai thích thú chơi game thể thao và trò chơi đánh bạc.
KUBET được biết đến kèm theo kỹ thuật bảo mật ưu việt và nền tảng độc nhất, yểm trợ đảm bảo tối đa thông tin người tham gia. Nhà cái này đưa ra đầy đủ chương trình khuyến khích đặc sắc như thể nạp lần kế tiếp, khuyến mãi 50%.
BET365 chính là nhà cái chơi game thể thao ưu việt trên châu Á, nổi bật kèm theo các tỷ lệ kèo châu Á, tài xỉu và live thể thao. Đây là tuyển chọn ưu việt dành cho những ai thích thú đặt cược thể thao.
FUN88 không chỉ mỗi cung ứng tỷ suất thưởng hấp dẫn nhất song cũng cung cấp đầy đủ ưu đãi ưu đãi riêng biệt tương tự như thưởng 108K Freebet và mã đặt cược thể thao SABA nhận được 10,888K.
New88 thu hút được người tham gia với các ưu đãi giảm giá hấp dẫn nhất như trả lại 2% không hạn chế và mưa phần thưởng liên tục. Chúng tượng trưng cho một trong các nhà cái hiện đang thu hút nhiều sự quan tâm xuất phát từ cộng đồng chơi game.
AE888 vượt trội với gói trao 120% lần khởi đầu gửi tiền đá gà
Vâng, tôi sẽ tiếp tục từ đoạn cuối của văn bản:
AE888 nổi bật hơn bên cạnh ưu đãi trao 120% lần đầu nạp đấu gà và các chương trình ưu đãi hấp dẫn khác biệt. Đây đại diện cho nhà cái độc quyền cung cấp sảnh SV388.
FI88 lôi cuốn người sử dụng với mức bồi thường ưu việt kết hợp với các gói thưởng tạo tài khoản hấp dẫn. Tất cả tượng trưng cho chọn ra tuyệt vời đối với những người ưa chuộng trò chơi bài và trò chơi đánh bạc.
F8BET nổi bật bên cạnh ưu đãi trao tạo tài khoản khởi đầu lên đến 8,888,888 VNĐ kết hợp với cùng với nhà phân phối phần thưởng 60%. Nó tượng trưng cho nhà cái đáng tin tưởng đối với mọi người muốn thu lợi qua cá cược online.
FB88 chính là một trong một trong những nhà cái đáng tin tưởng hàng đầu hiện nay bên cạnh các chương trình khuyến khích hấp dẫn nhất như hoàn trả cược xâu 100% và ưu đãi 150% nếu tham gia vào khu vực nổ hũ.
5 Tiêu Chí Đánh Giá Nhà Cái Uy Tín
Các trò chơi tuyệt vời: Được cung cấp từ các đơn vị phát triển hàng đầu, đảm nhận kết cục không thể dự đoán và không xuất hiện sự can thiệp.
Chăm sóc hỗ trợ khách hàng: Nhóm CSKH tuyệt vời, yểm trợ liên tục thông qua nhiều phương tiện.
Trao vượt trội: Tỷ lệ ưu đãi lôi cuốn và thuận tiện thực hiện, đơn giản lấy ra.
Bảo đảm đảm bảo: Công nghệ an toàn tiên tiến, bảo vệ giữ gìn thông tin người sử dụng.
Chống gian lận: Áp dụng chiến lược ngăn chặn gian lận rõ ràng, đảm bảo quyền lợi người sử dụng.
Nếu bạn có vài câu hỏi nào trải nghiệm đánh bạc, xin kiểm tra mục FAQ tại Trang web uy tín hàng đầu để tìm hiểu chi tiết hơn về các nhà cái kết hợp với ưu đãi mà họ sở hữu.
besifloxacin uk – buy generic sildamax order sildamax
ทดลаёаё‡а№ЂаёҐа№€аё™аёЄаёҐа№‡аёаё• pg
купить права категория б
Даркнет, искони стал знаменит как область, внутри которой разрешено купить практически разнообразные товары наряду с опции, не исключая схожие, что присутствуют за рамками юриспруденции.
Ключевым примером таких криминальных услуг является шанс получить права категории B согласно общемировой градации — класс “В”).
Многие субъектов, заинтересованные обойти стандартных тестирований или пренебречь нормы, анализируют способность получить документы категории “В” в даркнете.
При этом схожая получение связана посредством обширными вызовами и законодательными итогами, могущие стать значительно сложнее, чем всего лишь безуспешная операция.
купить карту с балансом
Подпольный интернет, сокрытая область онлайн-пространства, прославлен с имеющимися подпольными рынками, на которых имеются продукты и предложения, которые не удастся приобрести легальным путем.
Примером подобных услуг являются банковские карты с балансом, что выставляются на продажу злоумышленниками по тарифам, существенно дешевле их номинальной цены.
Среди ряда людей, стремящихся быстро обогатиться, возможность купить пластиковую карту с остатком на подпольном рынке может выглядеть выгодной.
Однако за подобными покупками таятся значительные проблемы и нормативные исходы, в отношении которых очень важно осведомляться.
Каким способом осуществляются предложения о продаже по достанию пластиковых карт с остатком?
На подпольном рынке можно найти большое число предложений по продаже пластиковых карт с балансом. Подобные карты могут быть в виде авансовыми, а также ассоциированными с банковскими счетами, и на которых, как утверждается, заранее внесены деньги.
Обычно реализаторы сообщают, будто бы пластиковая карта включает определенную количество, которые разрешено тратить на покупок и снятия денежных средств из денежных средств из банкоматов.
Расценка на такие пластиковые карты может варьироваться в соответствии с от объявленного баланса и вида платёжной карты. Например, банковскую карту с деньгами $5000 вполне могут реализовывать за $500, что это заметно менее реальной стоимости.
game tặng 100k trải nghiệm
Dưới đây là văn bản với các từ được thay thế bằng các cụm từ đề xuất (các từ đồng nghĩa) được đặt trong dấu ngoặc nhọn :
Tốt nhất 10 Nhà khai thác Đáng tin cậy nhất Hiện tại (08/2024)
Đặt cược số đã biến thành một trào lưu thịnh hành tại Việt, và việc chọn lựa nhà cái đáng tin tưởng là điều vô cùng cần thiết để đảm đương cái trải đặt cược bảo đảm và công bằng. Bên dưới là danh sách 10 ông lớn nhà cái uy tín nhất hiện nay, được phổ biến bởi trang nhận định hàng đầu Top10VN.
ST666 được xem là một trong những nhà cái lớn nhất lẫn đáng tin tưởng nhất hiện tại. Cùng với chăm sóc khách hàng xuất sắc, yểm trợ 24/7 kết hợp các dịch vụ giảm giá đặc sắc như thưởng 110% nếu ký quỹ lần ban đầu, chúng quả quyết là sự chọn lựa hàng đầu dành cho khách hàng.
RGBET nổi bật hơn bên cạnh dịch vụ đảm bảo lỗ thể thao đến 28,888K, kết hợp với bồi thường máy đánh bạc 2% không ngừng. RGBET đại diện cho lựa chọn hoàn hảo dành cho những ai yêu thích chơi game thể thao và trò chơi đánh bạc.
KUBET được biết đến cùng với công nghệ an toàn cao và nền tảng độc nhất, yểm trợ bảo đảm hoàn toàn chi tiết người tham gia. Nhà cái này đưa ra đầy đủ dịch vụ giảm giá đặc sắc như thể tạo tài khoản lần thứ hai, khuyến mãi 50%.
BET365 tượng trưng cho nhà cái đặt cược thể thao hàng đầu trong khu vực châu Á, nổi trội với các kèo châu Á, cược tài xỉu và live thể thao. Chúng tượng trưng cho chọn ra hoàn hảo đối với những người mê mẩn cá cược thể thao.
FUN88 không chỉ mỗi cung ứng mức tặng đặc sắc song cũng đưa ra đa dạng gói khuyến khích vượt trội như thể ưu đãi 108K Freebet và mã voucher cá cược thể thao SABA đến 10,888K.
New88 thu hút được người chơi kèm theo các dịch vụ giảm giá hấp dẫn nhất như thể hoàn lại 2% vô hạn và tặng quà tặng liên tục. Đây đại diện cho một trong những nhà cái vừa thu hút đầy đủ sự quan tâm đến từ cộng đồng cá cược.
AE888 vượt trội với gói ưu đãi 120% lần đầu nạp đá gà
Vâng, tôi sẽ tiếp tục từ đoạn cuối của văn bản:
AE888 nổi bật hơn kèm theo gói trao 120% lần đầu tiên tạo tài khoản đấu gà và các gói khuyến khích hấp dẫn nhất khác. Nó chính là nhà cái chuyên dụng đưa ra khu vực SV388.
FI88 thu hút người tham gia bên cạnh tỷ lệ bồi thường cao kết hợp với các chương trình thưởng tạo tài khoản đặc sắc. Chúng đại diện cho sự chọn lựa hoàn hảo cho tất cả thích thú trò chơi bài và game slot.
F8BET vượt trội cùng với gói tặng ký quỹ đầu nhận được 8,888,888 VNĐ cùng với với đại lý phần thưởng 60%. Đây đại diện cho nhà cái đáng tin cậy đối với mọi người muốn thu lợi qua chơi game online.
FB88 đại diện cho một trong một trong những nhà cái đáng tin được ưa chuộng nhất hiện nay cùng với các gói khuyến mãi hấp dẫn như hoàn trả cược liên tiếp 100% và trao 150% lúc góp mặt khu vực jackpot.
5 Tiêu Chí Đánh Giá Nhà Cái Uy Tín
Game tuyệt vời: Được phát hành do các nhà sản xuất uy tín nhất, đảm đương kết quả may rủi và không xuất hiện sự ảnh hưởng.
Phục vụ chăm sóc người chơi: Tập thể chăm sóc người chơi tuyệt vời, yểm trợ quanh ngày sử dụng nhiều kênh liên lạc.
Tặng hấp dẫn nhất: Mức trao hấp dẫn và dễ dàng thực hiện, đơn giản rút ra.
Đảm bảo bảo đảm: Hệ thống an toàn tiên tiến, bảo vệ an toàn thông tin khách hàng.
Chống gian lận: Có biện pháp bảo vệ khỏi gian lận rõ ràng, giữ gìn quyền lợi người tham gia.
Nếu bạn có những câu hỏi liên quan đến thực hiện đặt cược, vui lòng kiểm tra đoạn FAQ trên Trang web top 10 nhằm tìm hiểu thêm trong các nhà cái lẫn ưu đãi mà họ cung cấp.
карты с пин кодом с деньгами
Даркнет, скрытая сегмент глобальной сети, известен своими подпольными рынками, где предлагаются объекты и услуги, что нельзя достать легальным путем.
Примером этих предложений представляют собой банковские карты с остатком, которые предлагаются преступниками по ценам, существенно меньшие их номинальной стоимости приобретения.
Для большинства людей, заинтересованных в быстро получить прибыль, предложение приобрести карту с денежными средствами на подпольном рынке может восприниматься заманчивой.
Но за такими транзакциями таятся большие риски и юридические последствия, в отношении которых необходимо быть в курсе.
Каким образом осуществляются объявления по достанию пластиковых карт с балансом?
На подпольном рынке можно найти большое количество объявлений по сбыту карт с остатком. Такие банковские карты могут быть в виде авансовыми, а также связанными к банковским счетам, и на которых, как сообщается, ранее внесены финансовые средства
Чаще всего поставщики декларируют, что якобы карта содержит фиксированную количество, что именно можно применять в качестве приобретений а также изъятия денежных средств с использованием банкоматов.
Тариф на данные пластиковые карты может быть разной в соответствии с по заявленного остатка и с разновидности платёжной карты. Как пример, карту с балансом $5000 вполне могут предложить за $500, что и заметно ниже номинала.
Подпольный интернет, скрытая область онлайн-пространства, известен с их черными рынками, на которых имеются услуги и сервисы, которые именно не удастся получить открыто.
Одно из этих предложений являются платёжные карты с денежными средствами, которые именно выставляются на продажу нарушителями за стоимость, намного более дешевле их номинальной стоимости.
Среди ряда потребителей, намеревающихся быстро обогатиться, идея достать карту с балансом в даркнете может восприниматься привлекательной.
Вместе с тем за подобными операциями кроются существенные угрозы и правовые итоги, касательно которых необходимо иметь представление.
Как действуют объявления по получению платёжных карт с денежными средствами?
На теневом рынке предлагаются большое число предложений о продаже по продаже пластиковых карт с остатком. Данные платёжные карты могут быть в виде авансовыми, так и привязанными к банковским счетам, и где, как утверждается, предварительно зачислены денежные средства.
Типично продавцы утверждают, будто бы платёжная карта обладает фиксированную величину, которые именно разрешено применять для оплаты товаров и услуг или получения наличности посредством банкоматов.
Расценка на такие пластиковые карты может быть разной в соответствии с от декларированного остатка наряду с категории карты. Так, банковскую карту с деньгами $5000 могут продавать по цене $500, что именно существенно меньше номинальной стоимости.
Объявления по приобретению данных пластиковых карт зачастую дополняются “гарантиями” от имени реализаторов, которые ими декларируют, что карта обязательно станет функционировать, и гарантируют содействие в случае возникновения проблем. Но в реальности аналогичные “”заверения” не так много ценность в мире подпольного рынка, где операции проводятся без раскрытия личности, при этом приобретающий практически абсолютно ничем не обеспечен гарантиями.
Объявления по получению таких пластиковых карт зачастую включают “”обещаниями” от источников, которые ими утверждают, что фактически карта непременно окажется показывать работоспособность, и дают помощь при наступления неполадок. Тем не менее на самом деле подобные “”обещания” мало что ценность в сфере подпольного рынка, в пределах которого сделки заключаются конфиденциально, при этом приобретающий в действительности каким-либо образом не застрахован.
Dưới đây là văn bản với các từ được thay thế bằng các cụm từ đề xuất (các từ đồng nghĩa) được đặt trong dấu ngoặc nhọn :
Đỉnh 10 Nhà cái Đáng tin cậy Hiện tại (08/2024)
Đặt cược trực tuyến đã trở thành một xu hướng rất phổ biến tại VN, và việc tuyển chọn nhà cái đáng tin tưởng là chuyện hết sức cần thiết để bảo đảm trải nghiệm cá cược an toàn và không thiên vị. Dưới đây là danh sách 10 ông lớn nhà cái đáng tin cậy nhất ngày nay, được tổng hợp bởi trang đánh giá hàng đầu Danh sách 10 ông lớn.
ST666 nhận định là một trong những nhà cái lớn và đáng tin cậy hàng đầu hiện nay. Với hỗ trợ người sử dụng chuyên nghiệp, yểm trợ không ngừng lẫn với các ưu đãi khuyến mãi hấp dẫn nhất như trao 110% đương nạp lần khởi đầu, tất cả quả quyết là lựa chọn hàng đầu dành cho người chơi.
RGBET nổi bật cùng với ưu đãi bảo hiểm thua lỗ thể thao tới 28,888K, kết hợp với trả lại trò chơi đánh bạc 2% hàng ngày. RGBET đại diện cho sự chọn lựa hoàn hảo với những người ưa chuộng chơi game thể thao và trò chơi đánh bạc.
KUBET được biết đến kèm theo kỹ thuật bảo vệ hàng đầu và máy chủ riêng, trợ giúp bảo đảm tối đa chi tiết người chơi. Nhà cái này đưa ra đa dạng dịch vụ khuyến khích hấp dẫn nhất như nạp lần hai, khuyến mãi 50%.
BET365 là nhà cái chơi game thể thao ưu việt trong các nước châu Á, nổi bật hơn bên cạnh các odds châu Á, cược tài xỉu và phát sóng trực tiếp thể thao. Chúng đại diện cho chọn ra hoàn hảo đối với những ai ưa chuộng cá cược thể thao.
FUN88 không chỉ là sở hữu mức độ tặng đặc sắc song cũng sở hữu rất nhiều chương trình khuyến mãi vượt trội giống như ưu đãi 108K Freebet và mã đặt cược thể thao SABA nhận được 10,888K.
New88 thu hút được người sử dụng cùng với các dịch vụ khuyến khích đặc sắc giống như hoàn trả 2% không giới hạn và ưu đãi quà tặng mỗi ngày. Nó là một trong các nhà cái vừa hấp dẫn rất nhiều sự quan tâm của người chơi đánh bạc.
AE888 vượt trội bên cạnh gói ưu đãi 120% lần khởi đầu ký quỹ đá gà
Vâng, tôi sẽ tiếp tục từ đoạn cuối của văn bản:
AE888 nổi bật hơn bên cạnh dịch vụ thưởng 120% lần đầu tiên gửi tiền trận gà và các chương trình ưu đãi hấp dẫn đặc biệt. Nó là nhà cái chuyên biệt cung ứng sảnh SV388.
FI88 thu hút người chơi kèm theo tỷ suất bồi thường vượt trội bên cạnh các dịch vụ ưu đãi tạo tài khoản hấp dẫn nhất. Chúng đại diện cho lựa chọn vượt trội với những ai thích thú game bài và trò chơi đánh bạc.
F8BET vượt trội bên cạnh gói ưu đãi tạo tài khoản khởi đầu nhận được 8,888,888 VNĐ cùng với với người quản lý tiền thưởng 60%. Tất cả đại diện cho nhà cái đáng tin tưởng cho tất cả muốn tăng thu nhập từ đánh bạc trực tuyến.
FB88 tượng trưng cho một trong một trong những nhà cái đáng tin tưởng nhất bây giờ với các dịch vụ ưu đãi lôi cuốn tương tự như bồi thường cược nhiều ván 100% và ưu đãi 150% khi tham gia vào sảnh chơi trò chơi may rủi.
5 Tiêu Chí Đánh Giá Nhà Cái Uy Tín
Các sản phẩm game chất lượng: Được phát hành bởi các nhà cung cấp nổi tiếng, đảm nhận kết cục không thể dự đoán và không có sự can thiệp.
Chăm sóc hỗ trợ khách hàng: Đội ngũ chăm sóc khách hàng tuyệt vời, yểm trợ liên tục sử dụng rất nhiều phương tiện.
Ưu đãi hấp dẫn nhất: Tỷ suất ưu đãi hấp dẫn và dễ dàng thực hiện, dễ dàng rút vốn.
Bảo vệ không rủi ro: Kỹ thuật bảo vệ tiên tiến, bảo vệ bảo vệ thông tin cá nhân người chơi.
Ngăn ngừa gian lận: Thực hiện chiến lược chống gian lận minh bạch, giữ gìn tài sản người chơi.
Nếu bạn có những thắc mắc liên quan đến hoạt động cá cược, hãy tham khảo phần FAQ được cung cấp trên Trang web uy tín hàng đầu với mục đích tìm hiểu chi tiết hơn về các nhà cái cùng với sản phẩm mà họ cung cấp.
даркнет тг
Развитие мессенджеров, таких как Тelegram, посетители андеграунда нашли новые методы контакта. Telegram, известный своей концепцией конфиденциальности и навыком создания закрытых чатов, превратился известным среди тех, кто добивается конфиденциальность и защищенность.
При указанных группах разрешено получить предложения про продаже наркотиков, поддельных материалов, вооруженных средств и разнообразных нелегальных артикулов. Некоторые группы помимо этого предлагают сведения о способах попасть на теневым интернет-ресурсам, о применении безопасного обозревателя либо о приемах обеспечения анонимность при интернете.
Как правило эти сообщества ограничены, и с целью доступа на данные нужно приглашение либо же выполнение установленных условий.
В сравнении с скрытых веб-узлов, закрытые каналы при мессенджере удобнее для пользования и не нуждаются установки особого ПО. Клиенты могут проникать в материалам и предложениям непосредственно с использованием Телеграм, что процесс преобразует подобные группы существенно открытыми к большого количества пользователей. Тем не менее, как и в случае при даркнет-сайтами, задействование подобных групп сопряжено с существенными рисками.
AML check online
AML Checks – is a essential method employed by organizations and commercial players to verify the fact companies are not engaging with persons or companies engaged in unlawful transactions.
Such algorithm encompasses verifying the data of buyers through numerous records, among which prohibition inventories, high-level officials (PEP) inventories and additional control lists. Within the environment of cryptocurrencies, AML screening systems help identify and reduce probabilities associated with possible financial crimes activities.
In the course of executing AML screening, performers often analyze the listed criteria:
Customer Identity – verifying the credentials of the individual or organization engaged in the transfer, with the aim to that they do not included in any monitoring lists.
Transaction Characteristics – examining and analyzing transfer schemes for detection of certain doubtful having is likely to indirectly indicate financial crimes.
Blockchain Analysis – employing crypto asset tracing means in order to identify the flows of decentralized money and determine any connections to unlawful activities.
Anti-Money Laundering checks is not a single activity. It serves as a regular algorithm which helps verify that enterprises uphold compatible with rules and do not unintentionally engage in criminal practices. Regular Anti-Money Laundering monitoring online procedures ensure enterprises to update customer data and stay informed about potential fluctuations in their risk assessment.
The Functions of Anti-Money Laundering Check Online Tools
Anti-Money Laundering analysis online systems act as tools that provide automated AML screening systems. These services crucially important for enterprises acting in the decentralized finance area, where the risk of dealing with unlawful resources is higher because of the anonymous nature of decentralized money.
апл центр москва
probenecid order online – buy carbamazepine 400mg pill tegretol 200mg without prescription
purchase celecoxib generic – celebrex brand order indomethacin 75mg
Профессиональный сервисный центр по ремонту сотовых телефонов, смартфонов и мобильных устройств.
Мы предлагаем: ремонт сотовых телефонов рядом
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту сотовых телефонов, смартфонов и мобильных устройств.
Мы предлагаем: мастер по ремонту телефонов
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
It is perfect time to make some plans for the future and it’s time to be happy. I’ve read this post and if I could I wish to suggest you some interesting things or tips. Perhaps you could write next articles referring to this article. I desire to read even more things about it!
Профессиональный сервисный центр по ремонту квадрокоптеров и радиоуправляемых дронов.
Мы предлагаем:квадрокоптеры сервис
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
colospa cost – order colospa generic order cilostazol 100 mg sale
order diclofenac pill – order generic diclofenac order aspirin 75 mg generic
Профессиональный сервисный центр по ремонту ноутбуков и компьютеров.дронов.
Мы предлагаем:починить ноутбук в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
I’d incessantly want to be update on new content on this web site, saved to fav! .
Some really wonderful info , Glad I observed this.
priligy dapoxetine 60mg Nice and simple
замена венцов красноярск
Если осуществляется смена обвязки, то деревянный венец либо освобождается от напряжения и выполняется демонтаж с заменой, поскольку чтобы заменить подъём строения не превышает 10 см сантиметров, которое не выступает значительным даже для внутренней оформления.
нижняя балка или венец из листвяка более надежнее и успешно доказал свою надежность благодаря своей крепостью и сопротивляемостью к разрушению. Тем не менее, ее обязательно нужно обработать при помощи антибактериального препарата, как и другие перекладины.
Наше предприятие занимается не только ремонтом объектов, а также улучшением полов. Наши заказчики зачастую оформляют заказ на утепленные полы и перекрытия с тепловой термоизоляцией мы Комплектуем заказчика комплектующими и предоставляем специальные расценки.
наш телефон +7(391)29-29-699
VPS разнообразные серверы, скорость сети 1000mb,
выгодные стоимость
Большой диапазон настроек по любым нужды. Вы можете подобрать наилучший тариф, исходя из ваших нужд
Облачные серверы AMD EPYC — Сделайте ваш хостинг
Cloud-серверы Intel Gold
Обычные серверы, Аренда обычного сервера
Hi-CPU серверы
Выделенные серверы — аренда высокопроизводительных выделенных серверов
Высокопроизводительные серверы работающие на топовых процессоров AMD EPYC. Частота процессора до 3.4-4 ГГц. Надежная скорость сети к сети интернет
Круглосуточная техническая помощь. Наши специалисты всегда готовы моментально оказать помощь в любой ситуации., множество серверов — означает
Защита от дегенератов — доступны все сайты — интернет без цензуры
– Готовые шаблоны для сервиса WireGuard VPN, Outline VPN, 3X-UI VPN, Marzban VPN, IPsec VPN, OpenVPN
– Фиксированная стоимость в долларах США
– Оплата с карты РФ, криптовалютой, иностранной картой с использованием Stripe
Гибкая система оплаты. Мы предоставляем различные удобные способы оплаты, включая в себя кредитные карты, цифровые кошельки и цифровую валюту, с действующими скидками до 20%
Привлекательные цены. Тарифы наших сервисов ниже на 10-15 процентов, чем у аналогов, и при этом мы оказываем высококлассные услуги
Нет сбоев, стабильная и надежная эксплуатация безупречная.
ремонт apple watch
Замена венцов красноярск
Тогда, когда реализуется демонтаж с заменой венцов, в таком случае деревянная балка или освобождается от веса и выполняется демонтаж и монтаж, поскольку для проведения замены подъём не больше 10 см сантиметров, которое не выступает существенным даже для внутренних частей оформления.
нижний брус из лиственных существенно долговечней и успешно подтвердил свою надежность благодаря своей устойчивостью и стойкостью к разложению. Несмотря на это, данную балку точно следует обработать путем использования антибактериального раствора, наряду с и прочие балки.
Наша организация занимается не лишь ремонтом конструкций, но и обновлением основания пола. Потребители часто запрашивают утепленные полы с термической теплозащитой наши специалисты Укомплектовываем клиента материалами и обеспечиваем особые скидки.
Профессиональный сервисный центр по ремонту планетов в том числе Apple iPad.
Мы предлагаем: срочный ремонт айпада
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Когда реализуется замена нижних брёвен, в таком случае деревянный венец либо разгружается от напряжения и осуществляется смена, поскольку при замене поднятие не превышает 10-ти сантиметров, которое не выступает значительным включая для внутренностей обустройства.
нижняя балка или венец из лиственных пород более долговечно и надёжно и хорошо доказал свою надежность своей устойчивостью и сопротивляемостью к порче. При этом, данную балку обязательно необходимо обеспечивать защиту путем использования антибактериального средства, аналогично и другие стропила.
Наша компания занимается не только реконструкцией объектов, дополнительно улучшением полов. Клиенты зачастую оформляют заказ на теплые полы с тепловой термоизоляцией наша компания Обеспечиваем заявку материаллом и гарантируем специальные расценки.
Если вы искали где отремонтировать сломаную технику, обратите внимание – техпрофи
Профессиональный сервисный центр по ремонту радиоуправляемых устройства – квадрокоптеры, дроны, беспилостники в том числе Apple iPad.
Мы предлагаем: ремонт квадрокоптеров
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту ноутбуков и компьютеров.дронов.
Мы предлагаем:ремонт ноутбуков смартфонов
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем:сервис центры бытовой техники петербург
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Если вы искали где отремонтировать сломаную технику, обратите внимание – сервис центр в екатеринбурге
Если вы искали где отремонтировать сломаную технику, обратите внимание – ремонт бытовой техники
Если осуществляется замена венцов, тогда бревно или разгружается от нагрузки и происходит смена, поскольку для проведения замены поднятие не более 10 см сантиметров, что и не является существенным включая для внутренней отделки.
нижние брёвна или брус из лиственных более долговечнее и успешно показал свою надежность благодаря обладанию крепостью и стойкостью к порче. Тем не менее, ее обязательно необходимо защищать с помощью биоцидного раствора, наряду с и все остальные опоры.
Наша организация специализируется не исключительно восстановлением объектов, но и обновлением полов. Заказчики нередко запрашивают теплые полы и перекрытия с тепловой теплоизоляцией мы Обеспечиваем клиента материалами и гарантируем выгодные цены.
Если реализуется демонтаж с заменой нижних венцов, тогда брус или разгружается от нагрузки и осуществляется демонтаж и монтаж, так как при замене поднятие не выше десяти сантиметров, которое не является критичным даже для внутреннего отделки.
нижние брёвна или брус из лиственных пород более надежнее и эффективно подтвердил себя благодаря обладанию прочностью и нечувствительностью к разрушению. Тем не менее, ее также следует обработать путем использования противогрибкового средства, аналогично и другие перекладины.
Мы работает не только реконструкцией сооружений, но и улучшением полов. Наши заказчики зачастую оформляют заказ на теплые полы и перекрытия с термической теплозащитой наш персонал Укомплектовываем заказ материалами и предоставляем специальные расценки.
plinko
Digital casino platforms present an exhilarating range of gaming options, numerous of these these days integrate crypto as a method of payment. Of the most popular sites, BC Casino, Fortune Panda Casino, Axe Casino, and Bitkingz are getting more attention, whereas Bitstarz Casino is notable with numerous awards. Cloud Bet Casino is known for its status as a regulated crypto casino, providing security for players and fairness, meanwhile Fairspin as well as Mbit Casino deliver a broad selection of cryptocurrency games.
When it comes to dice-based games, cryptocurrency casinos for example BTC Dice bring an exhilarating experience, allowing gamblers to gamble with Bitcoin and other digital currencies such as Ether, LTC, DOGE, Binance Coin, and USDT.
For casino enthusiasts, deciding on the right provider matters. Thunderkick Casino, Play’n Go, Red Tiger, Quick Spin, Pragmatic, Playtech Casino, Nolimit City, NetEnt Casino, ELK Studios, and Microgaming are listed among the top game developers renowned for their unique slot games, high-quality graphics, and user-friendly interfaces.
Casino streaming has become an exciting style for gamblers to participate in casino games. Famous streamers such as Classy Beef, Roshtein, Labowsky, DeuceAce, and X-Posed stream their gameplay, commonly sharing big wins and sharing tips on top strategies for virtual casino gaming.
Additionally, services like BC Game Casino, Bitkingz Casino, and Rocketpot Casino also include Plinko-style games, a favorite game with basic rules but a high chance for high payouts.
Understanding gaming responsibility, cashback options, and anonymous gaming in virtual casinos is necessary for users aiming to enhance their gambling journey. Deciding on a secure wallet, looking for no-registration-required casinos, and learning strategies for games such as Aviator helps players stay informed while playing the excitement of the game.
Если вы искали где отремонтировать сломаную технику, обратите внимание – профи тех сервис новосибирск
срочный ремонт телефонов москва
Профессиональный сервисный центр по ремонту Apple iPhone в Москве.
Мы предлагаем: сервисный центр iphone в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту источников бесперебойного питания.
Мы предлагаем: ремонт источников бесперебойного питания
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
hyperliquid
ремонт телевизоров недорого
Если вы искали где отремонтировать сломаную технику, обратите внимание – профи ремонт
Если вы искали где отремонтировать сломаную технику, обратите внимание – профи тех сервис челябинск
плинко казино
Online casinos present an exhilarating array of games, a majority of them these days feature virtual currency as a transaction method. Of the best services, BC Game Casino, Fortune Panda Casino, Axe, and Bitkingz are becoming popular, whereas Bitstarz Casino shines through several awards. Cloud Bet Casino is recognized as being a licensed cryptocurrency casino, ensuring security for players and fair play, while Fairspin and Mbit deliver a large range of crypto-friendly games.
Regarding dice-based games, crypto casinos such as BTC Dice provide an exciting gambling experience, permitting gamblers to stake using Bitcoin and alternative cryptos including Ethereum, LTC, Dogecoin, Binance Coin, and Tether USD.
To online gambling enthusiasts, picking the best provider is important. Thunderkick, Play and Go, Red Tiger, Quickspin, Pragmatic Play, Playtech, Nolimit City Gaming, NetEnt, ELK Studio Games, and Microgaming are among the top game developers recognized for their creative slot games, high-quality graphics, and intuitive interfaces.
Casino streaming is now a popular way for players to engage with virtual casinos. Popular streamers for example Classy Beef, Roshtein Casino, Labowsky, Deuce Ace, and X-Posed share their gambling moments, often displaying large victories and offering tips on winning strategies for virtual casino gaming.
Additionally, platforms like BC Casino, Bitkingz, and Rocketpot Casino also feature Plinko games, a popular game with basic rules with large possibilities for huge rewards.
Comprehending responsible gaming, cashback options, and anonymous play in virtual casinos is important for players aiming to enhance their experience. Picking the right wallet, choosing no-sign-in platforms, and acquiring tactics for titles like Aviator allows players stay informed as they enjoy the thrill of casino gaming.
mestinon brand – imitrex 50mg sale imuran usa
hyperliquid
Профессиональный сервисный центр по ремонту варочных панелей и индукционных плит.
Мы предлагаем: сервис варочных панелей
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем:сервисные центры в екатеринбурге
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
buy rumalaya sale – shallaki canada endep 50mg pill
vibration analysis
The Significance of Vibrations Regulation Tools in Mechanical Systems
In industrial environments, machines as well as spinning equipment constitute the support of output. Yet, an of the highly prevalent problems which might impede the operation and lifetime is vibrations. Vibrations can bring about an variety of complications, from lowered accuracy as well as performance to increased erosion, in the end causing expensive downtime and fixes. This is the point where vibration management systems is vital.
Why Vibration Management is Necessary
Resonance within industrial equipment might result in several detrimental consequences:
Lowered Operational Productivity: Excessive oscillation might cause imbalances and imbalance, decreasing the effectiveness in the machinery. This can result in delayed output times and elevated energy consumption.
Greater Erosion: Constant oscillation increases the wear and tear in mechanical parts, resulting in more frequent maintenance as well as a possibility for unanticipated unexpected breakdowns. Such a scenario doesn’t merely increases production expenses as well as shortens the longevity in the equipment.
Security Concerns: Uncontrolled oscillation might present significant dangers both to the machinery and the equipment and the operators. In, severe cases, this may lead to cataclysmic equipment failure, jeopardizing operators along with leading to considerable devastation to the facility.
Accuracy and Quality Challenges: For sectors where demand high precision, for example industrial sectors as well as aerospace, resonance can lead to flaws during the production process, producing flawed products and greater waste.
Affordable Alternatives towards Oscillation Control
Investing in the vibration management systems proves not just necessary but a prudent choice for any business any industry that uses machines. The offered advanced vibration management systems work to built to remove oscillation in any machine as well as rotating equipment, ensuring seamless as well as effective performance.
Something that sets our systems from others is its its economic value. It is recognized that the value of affordability in the competitive market of today, thus our offerings include top-tier vibration regulation systems at costs that are reasonable.
Opting for our equipment, you are not just securing your machinery and boosting its efficiency as well as putting investment into the enduring success of your business.
Conclusion
Vibration management is an essential aspect in ensuring the efficiency, protection, along with lifetime of your industrial equipment. Using our economical vibration control equipment, you can ensure your operations run smoothly, all goods maintain top quality, and your workers remain safe. Never let oscillation undermine your business—make an investment in the proper tools now.
плинко казино
Digital gambling sites deliver an exhilarating array of gaming options, several of these these days incorporate cryptocurrency as a way to pay. Of the top casinos, BC Game Casino, Fortune Panda Casino, Axe, and Kingz Casino are growing in popularity, although Bit Starz stands out with numerous awards. Cloud Bet Casino is known for its status as a regulated crypto casino, guaranteeing player security and fair play, meanwhile Fair Spin Casino as well as MB Casino offer a wide range of crypto-compatible games.
Regarding casino dice games, virtual currency casinos like Bitcoin Dice provide a thrilling experience, permitting bettors to stake on Bitcoin and alternative cryptos for example ETH, LTC, DOGE, Binance Token, and USDT.
For casino enthusiasts, deciding on a reliable provider is important. Thunderkick Gaming, Play’n Go Casino, Red Tiger Gaming, Quickspin, Pragmatic Play Casino, Playtech Casino, NLC, NetEnt Casino, ELK, and MG Casino are among the best providers famous for their innovative slots, engaging graphics, and user-friendly interfaces.
Casino streams is now a new thrilling way for players to interact in casino games. Top streamers such as Classy Beef, Roshtein Casino, David Labowsky, DeuceAce, and X-Posed stream their gameplay, often displaying massive jackpots and providing tips on the best strategies for online gaming.
Additionally, sites like BC Game Casino, Bitkingz Casino, and Rocketpot Casino also feature Plinko bets, a widely played game with straightforward mechanics but a high chance for massive payouts.
Understanding responsible gambling, rebate offers, and playing anonymously in online crypto casinos is crucial for players aiming to enhance their gambling journey. Picking the best crypto wallet, choosing no-sign-in platforms, and learning strategies for games such as Aviator Casino Game enables users keep up-to-date while playing the excitement of the game.
ремонт фотоаппаратов в москве
hyperliquid
замена венцов красноярск
В случае если выполняется замена венцов, тогда деревянный венец также разгружается от веса и происходит демонтаж с заменой, так как чтобы заменить поднятие не более 10 см сантиметров, которое не является значительным в том числе для внутреннего отделки.
нижние брёвна или брус из лиственных существенно долговечнее и хорошо показал себя благодаря своей прочностью и стойкостью к порче. Однако, ее также точно нужно обработать через применение биоцидного состава, как и все опоры.
Мы специализируется не только перестройкой сооружений, дополнительно обновлением основания пола. Потребители часто запрашивают теплые полы и перекрытия с термической теплозащитой наши специалисты Обеспечиваем заказ всем необходимым для работы и обеспечиваем индивидуальные скидки.
volante de equilibrado con cesta de embrague
Dicho girador de nivelacion con recipiente de embrague constituye un procedimiento fundamental para asegurar el operacion ideal del propulsor y la transferencia de un automotor. El desequilibrio en la mencionada parte llega a provocar sacudidas, sonido, desgaste acelerado de los componentes e llegando a fallos. Anteriormente, el balanceo se ejecutaba luego de sacar el volante del motor, no obstante las desarrollos actuales facilitan ejecutar este metodo de forma directa en el transporte, lo que ahorra tiempo y costos.
Cual es el Desequilibrio?
El desajuste representa una situacion en la en la cual la peso de un elemento giratorio (en el presente caso, el rotativo de balanceo con cesta de embrague) se ubica de forma asimetrica en funcion de su eje de revolucion. Esta situacion produce cargas centrifugas que en consecuencia provocan sacudidas.
Principales causas del Desajuste del Girador de Balanceo con Canasto de Embrague:
Irregularidades de manufactura y ensamblaje: Aun minimas desviaciones en la estructura de los piezas podrian provocar falta de equilibrio.
Deterioro y averias: El funcionamiento prolongado, el temperatura elevada y los danos mecanicos pueden cambiar la peso y conducir en desajuste.
Instalacion o arreglo inadecuada: Una ensamblaje inadecuada de la canasto de embrague o arreglos inadecuados tambien podrian provocar desajuste.
Если вы искали где отремонтировать сломаную технику, обратите внимание – ремонт бытовой техники в челябинске
volante de equilibrado con cesta de embrague
Este volante de balanceo con recipiente de embrague representa un metodo critico para verificar el desempeno perfecto del motor y la transferencia de un vehiculo pesado. El falta de equilibrio en la presente pieza podria generar vibraciones, sonido, desgaste acelerado de los elementos e llegando a fallos. En el pasado, el equilibrado se realizaba luego de quitar el volador del motor, pero las tecnologias recientes posibilitan efectuar dicho procedimiento de manera directa en el vehiculo, lo cual reduce duracion y dinero.
Como se entiende el Desequilibrio?
El falta de equilibrio es una circunstancia en la que la masa de un cuerpo rotativo (en este escenario, el volador de nivelacion con compartimento de embrague) se ubica de manera desequilibrada en relacion con su punto de rotacion de movimiento circular. Esta situacion causa tensiones centrifugas que originan sacudidas.
Causas fundamentales del Desbalance del Rotativo de Equilibrado con Compartimento de Embrague:
Inexactitudes de produccion y union: Aun pequenas diferencias en la geometria de los elementos llegan a originar falta de equilibrio.
Desgaste y averias: El uso prolongado, el temperatura elevada y los desperfectos mecanicos llegan a alterar la cantidad y resultar en falta de equilibrio.
Colocacion o arreglo inadecuada: Una ensamblaje inapropiada de la compartimento de embrague o arreglos incorrectos tambien llegan a provocar desequilibrio.
slot853 login
slot853
Профессиональный сервисный центр по ремонту фото техники от зеркальных до цифровых фотоаппаратов.
Мы предлагаем: ремонт цифрового фотоаппарата
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
娛樂城推薦與優惠詳解
在現今的娛樂世界中，線上娛樂城已成為眾多玩家的首選。無論是喜歡真人遊戲、老虎機還是體育賽事，每個玩家都能在娛樂城中找到自己的樂趣。以下是一些熱門的娛樂城及其優惠活動，幫助您在選擇娛樂平台時做出明智的決定。
各大熱門娛樂城介紹
1. 富遊娛樂城
富遊娛樂城以其豐富的遊戲選擇和慷慨的優惠活動吸引了大量玩家。新會員只需註冊即可免費獲得體驗金 $168，無需儲值即可輕鬆試玩。此外，富遊娛樂城還提供首存禮金 100% 獎勵，最高可領取 $1000。
2. AT99娛樂城
AT99娛樂城以高品質的遊戲體驗和優秀的客戶服務聞名。該平台提供各種老虎機和真人遊戲，並定期推出新遊戲，讓玩家保持新鮮感。
3. BCR娛樂城
BCR娛樂城是一個新興的平台，專注於提供豐富的體育賽事投注選項。無論是足球、籃球還是其他體育賽事，BCR都能為玩家提供即時的投注體驗。
熱門遊戲推薦
WM真人視訊百家樂
WM真人視訊百家樂是許多玩家的首選，該遊戲提供了真實的賭場體驗，並且玩法簡單，容易上手。
戰神賽特老虎機
戰神賽特老虎機以其獨特的主題和豐富的獎勵機制，成為老虎機愛好者的最愛。該遊戲結合了古代戰神的故事背景，讓玩家在遊戲過程中感受到無窮的樂趣。
最新優惠活動
富遊娛樂城註冊送體驗金
富遊娛樂城新會員獨享 $168 體驗金，無需儲值即可享受全場遊戲，讓您無壓力地體驗不同遊戲的魅力。
VIP 日日返水無上限
富遊娛樂城為 VIP 會員提供無上限的返水優惠，最高可達 0.7%。此活動讓玩家在遊戲的同時，還能享受額外的回饋。
結論
選擇合適的娛樂城不僅能為您的遊戲體驗增色不少，還能通過各種優惠活動獲得更多的利益。無論是新會員還是資深玩家，都能在這些推薦的娛樂城中找到適合自己的遊戲和活動。立即註冊並體驗這些優質娛樂平台，享受無限的遊戲樂趣！
Если вы искали где отремонтировать сломаную технику, обратите внимание – выездной ремонт бытовой техники в краснодаре
Профессиональный сервисный центр по ремонту планшетов в Москве.
Мы предлагаем: отремонтировать планшет
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем:сервис центры бытовой техники новосибирск
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Если вы искали где отремонтировать сломаную технику, обратите внимание – ремонт техники в казани
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: ремонт крупногабаритной техники в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
buy baclofen 25mg generic – purchase piroxicam online cheap feldene 20mg oral
Профессиональный сервисный центр по ремонту видео техники а именно видеокамер.
Мы предлагаем: ремонт профессиональных видеокамер
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
娛樂城推薦與優惠詳解
在現今的娛樂世界中，線上娛樂城已成為眾多玩家的首選。無論是喜歡真人遊戲、老虎機還是體育賽事，每個玩家都能在娛樂城中找到自己的樂趣。以下是一些熱門的娛樂城及其優惠活動，幫助您在選擇娛樂平台時做出明智的決定。
各大熱門娛樂城介紹
1. 富遊娛樂城
富遊娛樂城以其豐富的遊戲選擇和慷慨的優惠活動吸引了大量玩家。新會員只需註冊即可免費獲得體驗金 $168，無需儲值即可輕鬆試玩。此外，富遊娛樂城還提供首存禮金 100% 獎勵，最高可領取 $1000。
2. AT99娛樂城
AT99娛樂城以高品質的遊戲體驗和優秀的客戶服務聞名。該平台提供各種老虎機和真人遊戲，並定期推出新遊戲，讓玩家保持新鮮感。
3. BCR娛樂城
BCR娛樂城是一個新興的平台，專注於提供豐富的體育賽事投注選項。無論是足球、籃球還是其他體育賽事，BCR都能為玩家提供即時的投注體驗。
熱門遊戲推薦
WM真人視訊百家樂
WM真人視訊百家樂是許多玩家的首選，該遊戲提供了真實的賭場體驗，並且玩法簡單，容易上手。
戰神賽特老虎機
戰神賽特老虎機以其獨特的主題和豐富的獎勵機制，成為老虎機愛好者的最愛。該遊戲結合了古代戰神的故事背景，讓玩家在遊戲過程中感受到無窮的樂趣。
最新優惠活動
富遊娛樂城註冊送體驗金
富遊娛樂城新會員獨享 $168 體驗金，無需儲值即可享受全場遊戲，讓您無壓力地體驗不同遊戲的魅力。
VIP 日日返水無上限
富遊娛樂城為 VIP 會員提供無上限的返水優惠，最高可達 0.7%。此活動讓玩家在遊戲的同時，還能享受額外的回饋。
結論
選擇合適的娛樂城不僅能為您的遊戲體驗增色不少，還能通過各種優惠活動獲得更多的利益。無論是新會員還是資深玩家，都能在這些推薦的娛樂城中找到適合自己的遊戲和活動。立即註冊並體驗這些優質娛樂平台，享受無限的遊戲樂趣！
娛樂城推薦與優惠詳解
在現今的娛樂世界中，線上娛樂城已成為眾多玩家的首選。無論是喜歡真人遊戲、老虎機還是體育賽事，每個玩家都能在娛樂城中找到自己的樂趣。以下是一些熱門的娛樂城及其優惠活動，幫助您在選擇娛樂平台時做出明智的決定。
各大熱門娛樂城介紹
1. 富遊娛樂城
富遊娛樂城以其豐富的遊戲選擇和慷慨的優惠活動吸引了大量玩家。新會員只需註冊即可免費獲得體驗金 $168，無需儲值即可輕鬆試玩。此外，富遊娛樂城還提供首存禮金 100% 獎勵，最高可領取 $1000。
2. AT99娛樂城
AT99娛樂城以高品質的遊戲體驗和優秀的客戶服務聞名。該平台提供各種老虎機和真人遊戲，並定期推出新遊戲，讓玩家保持新鮮感。
3. BCR娛樂城
BCR娛樂城是一個新興的平台，專注於提供豐富的體育賽事投注選項。無論是足球、籃球還是其他體育賽事，BCR都能為玩家提供即時的投注體驗。
熱門遊戲推薦
WM真人視訊百家樂
WM真人視訊百家樂是許多玩家的首選，該遊戲提供了真實的賭場體驗，並且玩法簡單，容易上手。
戰神賽特老虎機
戰神賽特老虎機以其獨特的主題和豐富的獎勵機制，成為老虎機愛好者的最愛。該遊戲結合了古代戰神的故事背景，讓玩家在遊戲過程中感受到無窮的樂趣。
最新優惠活動
富遊娛樂城註冊送體驗金
富遊娛樂城新會員獨享 $168 體驗金，無需儲值即可享受全場遊戲，讓您無壓力地體驗不同遊戲的魅力。
VIP 日日返水無上限
富遊娛樂城為 VIP 會員提供無上限的返水優惠，最高可達 0.7%。此活動讓玩家在遊戲的同時，還能享受額外的回饋。
結論
選擇合適的娛樂城不僅能為您的遊戲體驗增色不少，還能通過各種優惠活動獲得更多的利益。無論是新會員還是資深玩家，都能在這些推薦的娛樂城中找到適合自己的遊戲和活動。立即註冊並體驗這些優質娛樂平台，享受無限的遊戲樂趣！
Если вы искали где отремонтировать сломаную технику, обратите внимание – профи услуги
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервисные центры в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Если вы искали где отремонтировать сломаную технику, обратите внимание – ремонт бытовой техники
Если вы искали где отремонтировать сломаную технику, обратите внимание – профи ремонт
buy cheap generic diclofenac – purchase nimotop pill buy nimodipine online cheap
target88
target88
Профессиональный сервисный центр по ремонту стиральных машин с выездом на дом по Москве.
Мы предлагаем: ремонт стиральных машин сервисный центр москва
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: ремонт бытовой техники в казани
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Пеларгонии видовые: прекрасный выбор для твоего квартиры и огорода
Если вы подбираете цветы, которые станут радовать тебя своей внешним видом и ароматом, вместе с тем не требуя трудного ухода, разновидности герани — превосходный выбор. Этих цветы обладают неповторимыми характеристиками, которые делают их лидерами среди эстетических цветов.
Почему элитные пеларгонии?
Простота и легкость в уходе
Пеларгонии не запрашивают специальных условий для роста и быстро приспосабливаются к различным температурным режимам. Они идеально процветают как в жилище, так и на свежем воздухе. Не беспокойтесь о прихотливых цветах — герани требуется лишь увлажнять по степени исчезновения влаги почвы и наслаждаться их цветением.
Насыщенные и многообразные оттенки
Любой разновидность пеларгоний обладает свои исключительные оттенки и внешность. Разновидности, например как, Ю Полонез, впечатляют насыщенными оттенками и выразительными бутонами. Это растения, которые немедленно притягивают интерес и вносят яркие нотки в разном месте.
Приятный аромат, придающий комфорт
Пеларгонии не просто декорируют дом — они наполняют его нежным, незаметным запахом. Этот естественный благоухание способствует сформировать атмосферу спокойствия и спокойствия, а также работает как естественный репеллент для вредителей.
Длительное цветение
Сортовые герани продолжают долго радовать взоры своим цветением в течение нескольких недель. Люди будут радоваться их процветанием с начала теплого периода и до поздней сезона. Такое продолжительное процветание — уникальное свойство среди эстетических растений.
Идеальный выбор для различного пространства
Герани универсальны — их можно разводить как в контейнерах на оконных рамах, так и в на участке. Компактные растения, например ЮВ Кардинал, прекрасно выглядят в эстетичных контейнерах, а разновидности, как Магнус, превратятся в декорацией участка.
Для чего необходимо выбрать именно пеларгонии?
Этих цветы — не только элемент интерьера. Они существенно выделяются по сравнению с других видов из-за своей неприхотливости, красоте и длительному процветанию. Их насыщенные тона создают уникальную окружение, будь то в помещении или на садовом участке. Пеларгонии — это прекрасный сочетание внешнего вида и удобства.
Выбирайте пеларгонии — создайте в своем окружении эстетику без лишних трудностей!
Если вы искали где отремонтировать сломаную технику, обратите внимание – ремонт техники в перми
blackpanth
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: ремонт бытовой техники в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Если вы искали где отремонтировать сломаную технику, обратите внимание – тех профи
target88
target88
Профессиональный сервисный центр по ремонту игровых консолей Sony Playstation, Xbox, PSP Vita с выездом на дом по Москве.
Мы предлагаем: профессиональный ремонт игровых консолей
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту компьютерных видеокарт по Москве.
Мы предлагаем: ремонт видеокарт в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту фототехники в Москве.
Мы предлагаем: ремонт фотоаппаратов вспышек
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Подробнее на сайте сервисного центра remont-vspyshek-realm.ru
Профессиональный сервисный центр по ремонту компьютероной техники в Москве.
Мы предлагаем: ремонт компьютеров срочно
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту фото техники от зеркальных до цифровых фотоаппаратов.
Мы предлагаем: проектор ремонт
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Хочу поделиться опытом покупки в одном интернет-магазине сантехники. Решил обновить ванную комнату и искал место, где можно найти широкий выбор раковин и ванн. Этот магазин приятно удивил своим ассортиментом и сервисом. Там есть всё: от классических чугунных ванн до современных акриловых моделей.
Если вам нужна раковины цена , то это точно туда. Цены конкурентные, а качество товаров подтверждено сертификатами. Консультанты помогли с выбором, ответили на все вопросы. Доставка пришла вовремя, и установка прошла без проблем. Остался очень доволен покупкой и сервисом.
Профессиональный сервисный центр по ремонту компьютерных блоков питания в Москве.
Мы предлагаем: ремонт блоков питания
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Мой телефон перестал заряжаться, и я не знал, что делать. По совету друга обратился в этот сервисный центр. Мастера быстро нашли проблему и устранили её. Теперь мой телефон снова в строю! Рекомендую всем: ремонт мобильных телефонов в москве.
<a href=”https://remont-kondicionerov-wik.ru”>надежный сервис ремонта кондиционеров</a>
ремонт техники профи в самаре
Казино Kometa: Идеальный Шанс для Виртуальных Развлечений
В сфере цифровых казино Казино Kometa получило известность благодаря широкому ассортименту развлечений, щедрым бонусам и отличному обслуживанию. Эта система привлекает интерес клиентов во всех странах своими уникальными возможностями и частыми акциями. В этой статье мы проанализируем, почему Kometa является высоко оцениваемой площадок для азартных игр.
Преимущества Kometa
Одним из ключевых факторов, выделяющих Казино Kometa, является внимание на удовольствие клиентов. Платформа предлагает более 1000 развлечений, среди которых все найдет что-то по душе. Это предлагает традиционные игры, так и новые развлечения с уникальными опциями. Бонусом является то, что Kometa Casino обеспечивает постоянную помощь пользователей, создавая комфортное и надежное среду.
Ключевые особенности Kometa:
Год основания: 2024
Лицензия: Curacao
Количество игр: Огромное количество
Техподдержка: Постоянная чат и электронная почта
Мобильная версия: Доступно
Способы оплаты: Visa
Надежность: Шифрование SSL
Приветственные бонусы
Одним из главных плюсов Kometa являются щедрые приветственные бонусы для новых игроков. После входа на сайт пользователи могут воспользоваться к эксклюзивным промоакциям, что позволяет начать развлечение с небольшими вложениями. Эти поощрения создают благоприятные условия для новичков, создавая условия повысить свои успех с самого первого захода.
Большое количество развлечений
Казино Kometa гарантирует большое количество слотов на любой вкус. Пользователи могут играть традиционными играми, настольными играми, а также живыми играми. Благодаря передовым технологиям графики и музыкальному фону, любой пользователь может полностью погрузиться в игровой процесс.
Регулярные акции и мероприятия
Для игроков сайт постоянно проводит события и соревнования с выгодными наградами. Турниры проводятся каждый месяц, создавая развлечения более захватывающим и насыщенным. Это создает условия пользователям не только получать удовольствие от развлечениями, но и зарабатывать призы и выигрыши.
Зачем выбирать
Kometa — это идеальное сочетание множества развлечений, отличной поддержки и надежной системы. Система выделяется своим вниманием к пользователям и постоянным стремлением совершенствовать опыт пользователей. Неважно, новичок или профи, все сможет выбрать в Казино Kometa развлечение, которое сделает его пребывание на сайте интересным и приятным.
Присоединяйтесь к Казино Kometa и играйте с удовольствием адреналином и захватывающими играми каждый день!
Expression of MMPs is induced by growth factors like epithelial growth factors EGFs and receptor tyrosine kinase RTKs such as EGF receptor EGFR involving PI3K phosphatidylinositol 3 kinase and NF ОєB nuclear factor kappa light chain enhancer of activated B cells signaling cascades Sen Rhee Van den Steen et al can you buy priligy in usa
Профессиональный сервисный центр по ремонту компьютероной техники в Москве.
Мы предлагаем: ремонт стационарных компьютеров
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту камер видео наблюдения по Москве.
Мы предлагаем: ремонт систем видеонаблюдения
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервис центры бытовой техники нижний новгород
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
purchase mobic pills – toradol 10mg oral buy generic toradol over the counter
Онлайн-казино Kometa: Превосходный Выбор для Онлайн Азартных игр
В сфере виртуальных казино Kometa Casino завоевало признание благодаря широкому ассортименту слотов, выгодным поощрениям и первоклассному сервису. Эта система привлекает интерес пользователей во всех странах своими уникальными возможностями и частыми промо. В представленной описании мы обсудим, почему Казино Kometa является одной из лучших площадок для азартных игр.
Преимущества Kometa
Одним из ключевых факторов, отличающих Казино Kometa, является ориентация на потребности клиентов. Платформа гарантирует огромное количество слотов, среди которых любой сможет выбрать игру. Это предлагает привычные автоматы, а также современные развлечения с уникальными опциями. Плюсом является то, что Казино Kometa предлагает круглосуточную помощь клиентов, обеспечивая приятное и надежное среду.
Ключевые особенности Kometa Casino:
Год основания: 2024
Сертификация: Curacao
Ассортимент: Более 1000
Техподдержка: Постоянная чат и email
Мобильный доступ: Доступно
Способы оплаты: Mastercard
Безопасность: Шифрование SSL
Стартовые поощрения
Одним из главных плюсов Kometa считаются щедрые акции для новичков для новых игроков. После создания аккаунта игроки имеют право на к особым промоакциям, чем могут стартовать с меньшими затратами. Эти поощрения гарантируют благоприятные условия для начинающих, давая возможность улучшить свои шансы на победу с самого первого захода.
Огромный выбор игр
Kometa Casino предлагает широкий выбор слотов на любой вкус. Клиенты могут наслаждаться традиционными играми, настольными играми, а также играми с живыми дилерами. Благодаря отличной графике визуальных эффектов и звуковому сопровождению, любой пользователь может глубоко войти в игровой процесс.
Регулярные акции и мероприятия
Для каждого клиента система часто проводит турниры и соревнования с ценными призами. Акции проводятся каждый месяц, что делает развлечения интересным и захватывающим. Это позволяет игрокам не только играть слотами, но и зарабатывать дополнительные бонусы и призы.
Зачем выбирать
Kometa Casino — это идеальное сочетание широкого ассортимента, надежного сервиса и защищенной платформы. Система выделяется своим заботой о клиентах и постоянным стремлением совершенствовать развлечения. Без учета опыта, все откроет в Kometa то, что сделает его время на платформе увлекательным и комфортным.
Вступайте в Kometa и наслаждайтесь яркими эмоциями и захватывающими играми всегда!
Компания «Кинематика»: Надежные продукты для динамической сбалансированности и технической диагностики промышленных устройств
Предприятие «Кинематика» специализируется на изготовлении и изготовлении прецизионных приборов для технической балансировки и контроля техники. Продукция компании эксплуатируется для ремонта и налаживания разнообразных агрегатов, включая воздуходувки, шредеры, шарнирные валы, передаточные механизмы и станки для металла.
Основополагающие изделия компании:
1. Арбаланс устройство — компактный виброметр-балансировщик
Инструмент предназначен для динамической балансировки техники в заводской сборке в штатных подшипниках. Арбаланс обеспечивает отличные результаты балансировки с небольшими затратами. Среди его ключевых преимуществ:
Система автоматизированного анализа: работает автономно.
Спектральная диагностика: находят неполадки.
Измерение по двум плоскостям: даёт возможность фиксировать колебания параллельно в двух направлениях, повышая производительность процесса.
Цена: 84000 руб.
2. Модуль Балком-1А — компактный вибродиагностический прибор
Балком-1А разработан для балансировки валов в штатных подшипниках. Отличительной чертой является удобство эксплуатации и автоматический расчет. Также устройство оснащено:
Два канала измерения вибрации.
Спектральная диагностика для контроля состояния оборудования.
Цена: 73 тыс. руб.
3. Модуль Балком-2 — измерительная станция для станций балансировки
Балком-2 эксплуатируется в измерительных станциях для измерения вибраций. Он гарантирует надежность сбалансированности устройств и других механизмов в производстве.
Цена: от 90 000 руб. до 95 тыс. руб. в зависимости от сборки.
4. Система Балком-4 — для балансировки в нескольких плоскостях составных валов
Система Балком-4 разработан для сбалансированности карданных систем и внедряется в системах производства. Этот система предлагает высокую точность и надежность при многоплоскостной сбалансированности.
Цена: от 100000 руб. до 126000 руб..
Современные технологии мониторинга и технической диагностики
Предприятие «Кинематика» также разрабатывает системы для постоянного контроля состояния оборудования. Эти комплексы работают на бесконтактные датчики для виброизмерений и других показателей. Например, модуль Реконт даёт возможность контролировать механизмы редукторов по параметрам кинематической точности и оборудованию вращения.
балансировка центрифуги
Фирма «Кинематика»: Профессиональные продукты для производственной балансировки и технической диагностики техники
Компания ООО «Кинематика» фокусируется на проектировании и изготовлении высокоточных инструментов для технической балансировки и контроля техники. Продукция компании востребована для ремонта и техобслуживания различных промышленных устройств, включая воздуходувки, шредеры, валовые системы, передаточные механизмы и прецизионные станки.
Основополагающие продукты компании:
1. Модуль Арбаланс — мобильный система вибродиагностики
Система создан для динамической балансировки техники в заводской сборке в собственных узлах. Arbalance предлагает отличные результаты производственных процессов с сокращёнными издержками. Основные его преимущества:
Автоматизированная система расчета: работает автономно.
Анализ спектра вибрации: обнаруживают неисправности.
Двухканальная система: даёт возможность фиксировать вибрационные колебания параллельно в двух направлениях, повышая производительность процесса.
Цена: 84 000 руб.
2. Балансировочный прибор Балком-1А — компактный балансировочный виброметр
Система Балком-1А создан для балансировки вращательных механизмов в системных подшипниках. Ключевым преимуществом является простота использования и автоматизированный процесс расчета. Система дополнена:
Измерение вибрации в двух каналах.
Спектральный анализ для технической диагностики технического состояния оборудования.
Цена: 73 000 руб.
3. Balcom-2 — прибор для измерений для балансировочных станков
Балком-2 используется в балансировочных станках для измерения вибраций. Он даёт эффективность точного уравновешивания вращательных механизмов и прочих устройств в промышленности.
Цена: от 90 000 руб. до 95 тыс. руб. в зависимости от устройства.
4. Модуль Балком-4 — для балансировки в различных плоскостях карданных механизмов
Прибор Балком-4 применяется для балансировки составных карданных валов и используется в индустриальных установках. Этот устройство обеспечивает надежные результаты и надежность при многоплоскостной балансировке.
Цена: от 100000 руб. до 126000 руб..
Передовые системы отслеживания и проверки
Компания «Кинематика» также проектирует решения для беспрерывного отслеживания техники. Эти приборы применяют бесконтактными сенсорами для виброизмерений и различных параметров. Например, модуль Реконт позволяет отслеживать редукторы по точности работы механизмов и скорости вращения.
Профессиональный сервисный центр по ремонту кнаручных часов от советских до швейцарских в Москве.
Мы предлагаем: ремонт наручных часов
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Если вы искали где отремонтировать сломаную технику, обратите внимание – ремонт бытовой техники в тюмени
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервисные центры по ремонту техники в перми
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
сервисный центр кондиционеров
Профессиональный сервисный центр по ремонту парогенераторов в Москве.
Мы предлагаем: парогенератор сайт по ремонту
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Если вы искали где отремонтировать сломаную технику, обратите внимание – профи волгоград
Kometa casino online
Онлайн-казино Kometa: Лучший Вариант для Онлайн Азартных игр
В мире виртуальных казино Казино Kometa получило популярность благодаря разнообразию игр, выгодным поощрениям и отличному обслуживанию. Эта платформа захватывает внимание клиентов по всему миру своими особенными возможностями и регулярными акциями. В этой статье мы проанализируем, почему Kometa Casino считается одной из лучших площадок для азартных игр.
Преимущества Kometa Casino
Одним из ключевых факторов, отличающих Казино Kometa, является фокус на потребности пользователей. Платформа предоставляет свыше тысячи развлечений, среди которых все сможет выбрать игру. Это могут быть традиционные автоматы, и еще новые игры с инновационными функциями. Приятным дополнением является то, что Казино Kometa предлагает 24/7 помощь клиентов, гарантируя удобное и безопасное окружение.
Ключевые особенности Kometa Casino:
Дата запуска: 2024
Сертификация: Curacao
Выбор игр: Огромное количество
Техподдержка: Круглосуточная чат и email
Поддержка мобильных устройств: Имеется
Способы оплаты: Mastercard
Защита: Защита данных
Стартовые поощрения
Одной из главных особенностей Казино Kometa считаются привлекательные акции для новичков для новых игроков. Сразу после регистрации пользователи могут воспользоваться к особым бонусам, что дает возможность начать игру с небольшими вложениями. Эти поощрения гарантируют выгодные шансы для новых пользователей, давая возможность улучшить свои возможности выиграть с самого начала.
Широкий ассортимент игр
Kometa Casino гарантирует огромное разнообразие развлечений на все предпочтения. Клиенты могут играть классическими слотами, играми за столом, а также живыми играми. Благодаря передовым технологиям визуального сопровождения и аудио, любой пользователь может полностью погрузиться в процесс игры.
Постоянные события и турниры
Для каждого клиента система постоянно организует турниры и конкурсы с ценными призами. Мероприятия запускаются регулярно, придавая развлечения увлекательным и насыщенным. Это создает условия клиентам не только наслаждаться развлечениями, но и получать дополнительные бонусы и награды.
Почему Kometa Casino?
Kometa Casino — это оптимальное объединение множества развлечений, качественного обслуживания и защищенной платформы. Система выделяется своим фокусом на клиентах и постоянным стремлением совершенствовать игровой опыт. Неважно, новичок или профи, любой сможет выбрать в Kometa нечто, что позволит его время на платформе интересным и удобным.
Становитесь частью Kometa Casino и играйте с удовольствием яркими эмоциями и интересными развлечениями всегда!
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервисные центры в красноярске
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Если вы искали где отремонтировать сломаную технику, обратите внимание – сервис центр в уфе
brand omnicef 300mg – cleocin medication
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем:сервисные центры в ростове на дону
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
JILI SLOT GAMES: Sự Lựa Chọn Hàng Đầu Cho Các Tín Đồ Casino Trực Tuyến
JILI Casino là một nhà phát hành game nổi tiếng với nhiều năm kinh nghiệm trong ngành công nghiệp giải trí trực tuyến. Tại JILI, chúng tôi cam kết mang đến cho người chơi những trải nghiệm độc đáo và đẳng cấp, thông qua việc đổi mới không ngừng và cải thiện chất lượng từng sản phẩm. Những giá trị cốt lõi của chúng tôi không chỉ dừng lại ở việc tạo ra các trò chơi xuất sắc, mà còn tập trung vào việc cung cấp các tính năng vượt trội để đáp ứng nhu cầu của người chơi trên toàn cầu.
Sự Đa Dạng Trong Các Trò Chơi Slot
JILI nổi tiếng với loạt trò chơi slot đa dạng và hấp dẫn. Từ các slot game cổ điển đến những trò chơi với giao diện hiện đại và tính năng độc đáo, JILI Slot luôn đem đến cho người chơi những phút giây giải trí tuyệt vời. Các trò chơi được thiết kế với đồ họa sống động, âm thanh chân thực và những vòng quay thú vị, đảm bảo rằng người chơi sẽ luôn bị cuốn hút.
Ưu Điểm Nổi Bật Của JILI Casino
Đổi mới và sáng tạo: Mỗi trò chơi tại JILI Casino đều mang đến sự mới mẻ với lối chơi hấp dẫn và giao diện bắt mắt.
Chất lượng cao: JILI không ngừng cải tiến để đảm bảo mỗi sản phẩm đều đạt chất lượng tốt nhất, từ trải nghiệm người chơi đến tính năng trò chơi.
Nền tảng đa dạng: JILI Casino cung cấp nhiều loại game khác nhau, từ slot, bắn cá đến các trò chơi truyền thống, phù hợp với mọi sở thích của người chơi.
Chương Trình Khuyến Mại JILI
JILI Casino không chỉ nổi bật với chất lượng game mà còn thu hút người chơi bởi các chương trình khuyến mại hấp dẫn. Người chơi có thể tham gia vào nhiều sự kiện, từ khuyến mãi nạp tiền, hoàn trả đến các chương trình tri ân dành riêng cho thành viên VIP. Những ưu đãi này không chỉ tăng cơ hội chiến thắng mà còn mang lại giá trị cộng thêm cho người chơi.
Nổ Hủ City Và Các Trò Chơi Hấp Dẫn Khác
JILI không chỉ có slot games mà còn cung cấp nhiều thể loại game đa dạng khác như bắn cá, bài và nhiều trò chơi giải trí khác. Nổi bật trong số đó là Nổ Hủ City – nơi người chơi có thể thử vận may và giành được những giải thưởng lớn. Sự kết hợp giữa lối chơi dễ hiểu và các tính năng độc đáo của Nổ Hủ City chắc chắn sẽ mang lại những khoảnh khắc giải trí đầy thú vị.
Tham Gia JILI Casino Ngay Hôm Nay
Với sự đa dạng về trò chơi, các tính năng vượt trội và những chương trình khuyến mại hấp dẫn, JILI Casino là sự lựa chọn không thể bỏ qua cho những ai yêu thích trò chơi trực tuyến. Hãy truy cập trang web chính thức của JILI ngay hôm nay để trải nghiệm thế giới giải trí không giới hạn và giành lấy những phần thưởng hấp dẫn từ các trò chơi của chúng tôi!
娛樂城推薦
DB娛樂遊戲中心：最佳線上娛樂平台評價介紹
DB賭場，前身為PM娛樂城，於2023年徹底更名為【DB多寶遊戲】。這場品牌更新的階段，DB娛樂平台進一步專注於帶來多元的線上娛樂體驗，為玩家帶來更廣泛的遊戲類型與全新的遊戲服務。無論是百家樂、體育博彩還是其他常見遊戲，DB遊戲平台都能滿足玩家的期待。
多寶遊戲的誕生與發展 在亞洲娛樂市場中，DB娛樂網站飛速壯大，成為大量玩家的熱門選擇平台之一。隨著PM機構的品牌重塑，DB多寶遊戲聚焦於提升客戶體驗，並努力構建一個穩定、方便且公正的遊戲氛圍。從娛樂項目到交易系統，DB娛樂城都追求卓越，為玩家呈現首選的線上賭場體驗。
DB賭場的遊戲項目與優勢
百家樂遊戲 DB遊戲平台最為著名的是其豐富的百家樂玩法。平台提供多個版本的百家樂，包括常見百家樂和無佣金百家樂，滿足多樣化玩家的需求。透過實時荷官的同步互動，玩家可以體驗身臨其境的賭場體驗。
體育博彩 作為一個全面平台，DB賭場還呈現各類運動項目的投注服務。從足球賽事、籃球賽事到網球比賽等受歡迎賽事，玩家都可以隨時隨地參與體育博彩，享受比賽的快感與投注的樂趣。
促銷活動與獎金 DB娛樂城定期推出豐富的促銷優惠，為新舊會員呈現各種折扣與獎金。這些優惠不僅提高了遊戲的趣味性，還為玩家推動更多賺取紅利的選項。
DB賭場的口碑與亮點 在2024年的最新賭場排行榜中，DB娛樂網站獲得了優秀評價，並且因其多樣的遊戲選擇、快捷的提款效率和廣泛的促銷活動而廣受玩家喜愛。
https://generous-freesia-dc4vlg.mystrikingly.com/blog/b50ae6fc2dd
сервисный центре предлагает ремонт телевизоров на дому в москве недорого – ремонт телевизора москва
https://medium.com/@nsw5288/%EB%B9%84%EC%95%84%EA%B7%B8%EB%9D%BC-2%EC%95%8C-%EB%A8%B9%EC%9C%BC%EB%A9%B4-1058234842f0
Howdy! This is my first comment here so I just wanted to give a quick shout out and tell you I genuinely enjoy reading through your posts. Can you suggest any other blogs/websites/forums that go over the same topics? Thanks for your time!
https://pdx.eater.com/venue/46809/khun-pic-s-bahn-thai
cheap trihexyphenidyl online – purchase emulgel online cheap purchase emulgel cheap
Сервисный центр предлагает ремонт планшетов oysters недорого ремонт планшета oysters на дому
https://medium.com/@dqvchristopherwhite824/%EB%84%A4%EC%9D%B4%EB%B2%84-%EC%95%84%EC%9D%B4%EB%94%94-%EC%83%9D%EC%84%B1-%EC%8B%9C-%EC%A3%BC%EC%9D%98%ED%95%B4%EC%95%BC-%ED%95%A0-%EC%82%AC%ED%95%AD-1e7ff7203c15
Сервисный центр предлагает ремонт плоттера flora выездной ремонт плоттеров flora
купить строительную бытовку
Купить бытовку распашонку (лмдф) 184 900? (в т.ч. НДС)
Аренда бытовки распашонки (лмдф)
9 000? в месяц (в т.ч. НДС)
Внешний размер контейнера 5850х2400х2400(в).
Каркас стальной, верхняя и нижняя рама из промышленных сложногнутых профилей различной конфигурации, ширина верхнего пояса 160 мм, нижнего 120 мм, стойки стальные гнутые шестигранные 150х100 мм.
Кровля – лист стальной оцинкованный 0,5 мм, соединенный двойным стоячим фальцем по всей дине контейнера.
Стены каркасные из бруса 40х100, снаружи профилированный оцинкованный лист С-8.
Два окна ПВХ 900х1100(в) с поворотно-откидной створкой.
Если вы искали где отремонтировать сломаную технику, обратите внимание – профи ремонт
jili
JILI SLOT GAMES: Sự Lựa Chọn Hàng Đầu Cho Các Tín Đồ Casino Trực Tuyến
JILI Casino là một nhà phát hành game nổi tiếng với nhiều năm kinh nghiệm trong ngành công nghiệp giải trí trực tuyến. Tại JILI, chúng tôi cam kết mang đến cho người chơi những trải nghiệm độc đáo và đẳng cấp, thông qua việc đổi mới không ngừng và cải thiện chất lượng từng sản phẩm. Những giá trị cốt lõi của chúng tôi không chỉ dừng lại ở việc tạo ra các trò chơi xuất sắc, mà còn tập trung vào việc cung cấp các tính năng vượt trội để đáp ứng nhu cầu của người chơi trên toàn cầu.
Sự Đa Dạng Trong Các Trò Chơi Slot
JILI nổi tiếng với loạt trò chơi slot đa dạng và hấp dẫn. Từ các slot game cổ điển đến những trò chơi với giao diện hiện đại và tính năng độc đáo, JILI Slot luôn đem đến cho người chơi những phút giây giải trí tuyệt vời. Các trò chơi được thiết kế với đồ họa sống động, âm thanh chân thực và những vòng quay thú vị, đảm bảo rằng người chơi sẽ luôn bị cuốn hút.
Ưu Điểm Nổi Bật Của JILI Casino
Đổi mới và sáng tạo: Mỗi trò chơi tại JILI Casino đều mang đến sự mới mẻ với lối chơi hấp dẫn và giao diện bắt mắt.
Chất lượng cao: JILI không ngừng cải tiến để đảm bảo mỗi sản phẩm đều đạt chất lượng tốt nhất, từ trải nghiệm người chơi đến tính năng trò chơi.
Nền tảng đa dạng: JILI Casino cung cấp nhiều loại game khác nhau, từ slot, bắn cá đến các trò chơi truyền thống, phù hợp với mọi sở thích của người chơi.
Chương Trình Khuyến Mại JILI
JILI Casino không chỉ nổi bật với chất lượng game mà còn thu hút người chơi bởi các chương trình khuyến mại hấp dẫn. Người chơi có thể tham gia vào nhiều sự kiện, từ khuyến mãi nạp tiền, hoàn trả đến các chương trình tri ân dành riêng cho thành viên VIP. Những ưu đãi này không chỉ tăng cơ hội chiến thắng mà còn mang lại giá trị cộng thêm cho người chơi.
Nổ Hủ City Và Các Trò Chơi Hấp Dẫn Khác
JILI không chỉ có slot games mà còn cung cấp nhiều thể loại game đa dạng khác như bắn cá, bài và nhiều trò chơi giải trí khác. Nổi bật trong số đó là Nổ Hủ City – nơi người chơi có thể thử vận may và giành được những giải thưởng lớn. Sự kết hợp giữa lối chơi dễ hiểu và các tính năng độc đáo của Nổ Hủ City chắc chắn sẽ mang lại những khoảnh khắc giải trí đầy thú vị.
Tham Gia JILI Casino Ngay Hôm Nay
Với sự đa dạng về trò chơi, các tính năng vượt trội và những chương trình khuyến mại hấp dẫn, JILI Casino là sự lựa chọn không thể bỏ qua cho những ai yêu thích trò chơi trực tuyến. Hãy truy cập trang web chính thức của JILI ngay hôm nay để trải nghiệm thế giới giải trí không giới hạn và giành lấy những phần thưởng hấp dẫn từ các trò chơi của chúng tôi!
https://ko.anotepad.com/note/read/xrjfbcsf
https://hypothes.is/users/shepparduvg897
https://naveridbuy.exblog.jp/35859439/
https://umber-iris-dd3cm2.mystrikingly.com/blog/056c14d890b
https://ameblo.jp/naveridbuy/entry-12866332500.html
http://hawkee.com/profile/7310536/
Профессиональный сервисный центр по ремонту компьютеров и ноутбуков в Москве.
Мы предлагаем: ремонт ноутбуков apple москва
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
https://hallbook.com.br/blogs/313105/%EB%B9%84%EC%95%84%EA%B7%B8%EB%9D%BC-%EC%A0%9C%EB%84%A4%EB%A6%AD-%EC%A0%9C%ED%92%88-%EA%B0%80%EA%B2%A9%EA%B3%BC-%ED%9A%A8%EA%B3%BC-%EB%B9%84%EA%B5%90
https://gajweor.pixnet.net/blog/post/162189334
娛樂城
DB娛樂遊戲中心：最優線上娛樂網站評價介紹
DB娛樂城，前身為PM遊戲平台，於2023年全面更名為【DB多寶遊戲】。這場品牌轉型的階段，DB娛樂平台進而專注於推動綜合性的線上遊戲體驗，為玩家推動更豐富的遊戲選擇與革新的娛樂服務。無論是百家樂遊戲、運動投注還是其他流行遊戲，DB娛樂平台都能迎合玩家的期待。
多寶品牌的發展與發展 在亞洲賭場市場中，DB娛樂城迅速發展，成為眾多玩家的首要選擇平台之一。隨著PM機構的品牌更名，DB多寶遊戲致力於提升使用者體驗，並努力打造一個可靠、快速且公平的遊戲氛圍。從遊戲內容到支付方式，DB娛樂網站一直專注於卓越，為玩家呈現最佳的線上體驗。
DB娛樂網站的娛樂內容與亮點
百家樂遊戲 DB賭場最為著名的是其多元的百家樂項目。平台推出多個版本的百家樂，包括傳統百家樂和無佣金百家樂，符合不同玩家的需求。透過真人荷官的現場互動，玩家可以獲得逼真的現場氣氛。
體育博彩 作為一個多元化賭場，DB遊戲平台還呈現各類運動項目的博彩服務。從球賽、籃球遊戲到網球遊戲等流行體育項目，玩家都可以隨時隨地進行體育博彩，體驗賽事的刺激與投注的樂趣。
促銷活動與獎金 DB娛樂城定期推出廣泛的促銷方案，為新舊玩家推動各種福利與回饋。這些活動不僅提升了遊戲的趣味性，還為玩家推動更多贏取福利的機會。
DB賭場的評價與優勢 在2024年的最新線上娛樂平台排行榜中，DB娛樂城獲得了卓越評價，並且因其多樣的遊戲選擇、快捷的提款效率和廣泛的促銷活動而獲得玩家喜愛。
https://umber-iris-dd3cm2.mystrikingly.com/blog/1df903b065e
Купить бытовку под столовую 149 900? (в т.ч. НДС)
Аренда бытовок под столовую
8 000? в месяц (в т.ч. НДС)
внешний размер 6000х2400х2500(в);
окно ПВХ с поворотно-откидной створкой;
утепленные пол, потолок, стены;
отделка потолка панелями ПВХ;
отделка стен ДВП, линолеум на полу;
https://xn--w7-hs1izvv81cmb366re3s.mystrikingly.com/blog/ae4602cdfdc
https://telegra.ph/%EB%84%A4%EC%9D%B4%EB%B2%84-%EC%95%84%EC%9D%B4%EB%94%94-%EA%B1%B0%EB%9E%98-%EC%82%AC%EA%B8%B0-%EC%98%88%EB%B0%A9%EC%9D%84-%EC%9C%84%ED%95%9C-%ED%8C%81-09-20
https://viastoer.blogspot.com/2024/09/blog-post_60.html
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервисные центры в тюмени
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
jili city
JILI SLOT GAMES: Sự Lựa Chọn Hàng Đầu Cho Các Tín Đồ Casino Trực Tuyến
JILI Casino là một nhà phát hành game nổi tiếng với nhiều năm kinh nghiệm trong ngành công nghiệp giải trí trực tuyến. Tại JILI, chúng tôi cam kết mang đến cho người chơi những trải nghiệm độc đáo và đẳng cấp, thông qua việc đổi mới không ngừng và cải thiện chất lượng từng sản phẩm. Những giá trị cốt lõi của chúng tôi không chỉ dừng lại ở việc tạo ra các trò chơi xuất sắc, mà còn tập trung vào việc cung cấp các tính năng vượt trội để đáp ứng nhu cầu của người chơi trên toàn cầu.
Sự Đa Dạng Trong Các Trò Chơi Slot
JILI nổi tiếng với loạt trò chơi slot đa dạng và hấp dẫn. Từ các slot game cổ điển đến những trò chơi với giao diện hiện đại và tính năng độc đáo, JILI Slot luôn đem đến cho người chơi những phút giây giải trí tuyệt vời. Các trò chơi được thiết kế với đồ họa sống động, âm thanh chân thực và những vòng quay thú vị, đảm bảo rằng người chơi sẽ luôn bị cuốn hút.
Ưu Điểm Nổi Bật Của JILI Casino
Đổi mới và sáng tạo: Mỗi trò chơi tại JILI Casino đều mang đến sự mới mẻ với lối chơi hấp dẫn và giao diện bắt mắt.
Chất lượng cao: JILI không ngừng cải tiến để đảm bảo mỗi sản phẩm đều đạt chất lượng tốt nhất, từ trải nghiệm người chơi đến tính năng trò chơi.
Nền tảng đa dạng: JILI Casino cung cấp nhiều loại game khác nhau, từ slot, bắn cá đến các trò chơi truyền thống, phù hợp với mọi sở thích của người chơi.
Chương Trình Khuyến Mại JILI
JILI Casino không chỉ nổi bật với chất lượng game mà còn thu hút người chơi bởi các chương trình khuyến mại hấp dẫn. Người chơi có thể tham gia vào nhiều sự kiện, từ khuyến mãi nạp tiền, hoàn trả đến các chương trình tri ân dành riêng cho thành viên VIP. Những ưu đãi này không chỉ tăng cơ hội chiến thắng mà còn mang lại giá trị cộng thêm cho người chơi.
Nổ Hủ City Và Các Trò Chơi Hấp Dẫn Khác
JILI không chỉ có slot games mà còn cung cấp nhiều thể loại game đa dạng khác như bắn cá, bài và nhiều trò chơi giải trí khác. Nổi bật trong số đó là Nổ Hủ City – nơi người chơi có thể thử vận may và giành được những giải thưởng lớn. Sự kết hợp giữa lối chơi dễ hiểu và các tính năng độc đáo của Nổ Hủ City chắc chắn sẽ mang lại những khoảnh khắc giải trí đầy thú vị.
Tham Gia JILI Casino Ngay Hôm Nay
Với sự đa dạng về trò chơi, các tính năng vượt trội và những chương trình khuyến mại hấp dẫn, JILI Casino là sự lựa chọn không thể bỏ qua cho những ai yêu thích trò chơi trực tuyến. Hãy truy cập trang web chính thức của JILI ngay hôm nay để trải nghiệm thế giới giải trí không giới hạn và giành lấy những phần thưởng hấp dẫn từ các trò chơi của chúng tôi!
https://naveridbuy.exblog.jp/35658975/
DB娛樂平台：首選線上賭場評價介紹
DB遊戲平台，前身為PM娛樂網站，於2023年徹底更名為【DB多寶遊戲】。這次品牌更新的階段，DB娛樂平台進一步專注於帶來多元的線上賭場體驗，為玩家推動更廣泛的遊戲類型與創新的娛樂選項。無論是百家樂、運動博彩還是其他常見遊戲，DB遊戲平台都能迎合玩家的偏好。
多寶品牌的發展與發展 在亞洲線上娛樂市場中，DB娛樂網站快速發展，成為許多玩家的首選平台之一。隨著PM集團的品牌轉型，DB多寶遊戲專注於提升用戶體驗，並聚焦於構建一個穩定、便捷且合規的遊戲氛圍。從娛樂項目到交易系統，DB遊戲平台一直專注於卓越，為玩家帶來最佳的線上體驗。
DB賭場的遊戲類型與優勢
百家樂遊戲 DB娛樂城最為廣受歡迎的是其豐富的百家樂項目。平台提供多個版本的莊家遊戲，包括常見百家樂和免佣百家樂，滿足各類玩家的偏好。透過真人荷官的實時互動，玩家可以體驗身臨其境的遊戲氛圍。
體育博彩 作為一個多功能平台，DB娛樂網站還推出各類體育遊戲的投注服務。從球賽、籃球賽事到網球賽事等熱門賽事，玩家都可以隨處參與體育博彩，獲得賽事的緊張感與下注的刺激。
促銷活動與獎金 DB賭場定期推出豐富的促銷方案，為新舊會員呈現各種折扣與獎勵。這些優惠不僅提高了遊戲的刺激感，還為玩家帶來更多贏得紅利的可能性。
DB遊戲平台的評價與特點 在2024年的最新賭場排行榜中，DB娛樂網站獲得了極高評價，並且因其多樣的遊戲選擇、快捷的提款效率和持續的促銷活動而廣受玩家喜愛。
https://obedient-flamingo-dc4vl0.mystrikingly.com/blog/a030fd68b51
의사항해당 사이비아그라 구매 – 파워맨트는 영문 사이트이기 비아그라 구매 – 파워맨때문에 구입에 어려움이비아그라 구매 – 파워맨 있을
Профессиональный сервисный центр по ремонту кондиционеров в Москве.
Мы предлагаем: ремонт кондиционеров в москве цена
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту моноблоков в Москве.
Мы предлагаем: замена экрана моноблока
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
купить строительную бытовку
Купить офисный модуль 349 900? (в т.ч. НДС)
Аренда офисных модулей
9 000? в месяц (в т.ч. НДС)
Внешний размер контейнера 6055х2435х2750(в)
Окно ПВХ 1000х1200 с поворотно-откидной створкой
Ветро, гидро, пароизоляция – пленка ПВХ
Окраска металлокаркаса грунт-эмалью 3в1
Каркас стальной, верхняя и нижняя рама из промышленных сложногнутых профилей различной конфигурации, ширина верхнего пояса 210 мм, нижнего 180 мм, стойки стальные гнутые шестигранные 150х180 мм
https://ebony-raccoon-dc4vlj.mystrikingly.com/blog/61d56ceb8ea
https://inky-onion-dc4vlq.mystrikingly.com/blog/33da14ec78d
Профессиональный сервисный центр по ремонту планшетов в том числе Apple iPad.
Мы предлагаем: сервисный центр айпад в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
https://medium.com/@nsw5288/%EB%B9%84%EC%95%84%EA%B7%B8%EB%9D%BC-%EA%B5%AC%EB%A7%A4%EC%9D%98-%EC%98%AC%EB%B0%94%EB%A5%B8-%EC%A0%88%EC%B0%A8%EC%99%80-%EB%8B%A8%EA%B3%84-24facec76c89
https://funny-lion-dc4vln.mystrikingly.com/blog/f70eeb6f544
Backlinks – three steps
1: Stage – backlinks to the site in blogs and comments
Step 2: Backlinks via website redirects
3: Stage – Placement of the site on the sites of the analyzer,
example:
https://backlinkstop.com/
Explanation for stage 3: – only the main page of the site is placed on the analyzers, subsequent pages cannot be placed.
I only need a link to the main domain, if you give me a link to a social network or other resource that is not suitable for detection on the analyzer site, then I will take the third step through a google redirect
I do three steps in sequence, as described above
This backlink strategy is the most effective as the analyzers show the site keywords H1, H2, H3 and sitemap!!!
Show placement on scraping sites via TXT file
List of site analyzers 50 pcsI will provide the report as a text file with links.
order generic deltasone – elimite for sale online buy cheap permethrin
buy isotretinoin without prescription – deltasone 5mg oral buy deltasone 5mg generic
Профессиональный сервисный центр по ремонту посудомоечных машин с выездом на дом в Москве.
Мы предлагаем: ремонт посудомоечных машин на дому в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
rtpkantorbola
Kantorbola adalah situs gaming online terbaik di indonesia , kunjungi situs RTP kantor bola untuk mendapatkan informasi akurat rtp diatas 95% . Kunjungi juga link alternatif kami di kantorbola77 dan kantorbola99 .
https://lilac-grape-dc4vlw.mystrikingly.com/blog/1003365ca1d
https://ameblo.jp/naveridbuy/entry-12865279211.html
https://xn--oy2bo9bg4imgm5ikup.mystrikingly.com/blog/a9c260bf7b3
기에는 약의 상태를 알비아그라 구매 사이트려주는 상태창이 있다.비아그라 구매 사이트 상태창을 통해 약물을비아그라 구매 사이트 볼 수
Сервисный центр предлагает ремонт принтера polaroid на дому ремонт принтера polaroid рядом
https://ebony-lemon-dc4vlj.mystrikingly.com/blog/6cf18ce2985
Профессиональный сервисный центр по ремонту МФУ в Москве.
Мы предлагаем: где отремонтировать мфу в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
https://viastoer.blogspot.com/2024/09/blog-post_70.html
Kantorbola adalah situs gaming online terbaik di indonesia , kunjungi situs RTP kantor bola untuk mendapatkan informasi akurat rtp diatas 95% . Kunjungi juga link alternatif kami di kantorbola77 dan kantorbola99 .
I got this web site from my pal who informed me about this website and now this time I am browsing this web site and reading very informative articles at this place.
https://en.wikipedia.org/wiki/Nottingham_High_School
Профессиональный сервисный центр по ремонту принтеров в Москве.
Мы предлагаем: починить принтер москва
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
https://salmon-peach-dd3cm8.mystrikingly.com/blog/dfb5adc9b33
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем:сервис центры бытовой техники уфа
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
https://salmon-peach-dd3cm8.mystrikingly.com/blog/c327bc79164
https://umber-iris-dd3cm2.mystrikingly.com/blog/056c14d890b
https://gentle-heron-dc4vlr.mystrikingly.com/blog/e381c570ddc
kantorbola
Kantorbola adalah situs gaming online terbaik di indonesia , kunjungi situs RTP kantor bola untuk mendapatkan informasi akurat rtp diatas 95% . Kunjungi juga link alternatif kami di kantorbola77 dan kantorbola99 .
Профессиональный сервисный центр по ремонту плоттеров в Москве.
Мы предлагаем: ремонт плоттеров в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту объективов в Москве.
Мы предлагаем: объектив ремонт
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту серверов в Москве.
Мы предлагаем: цены на ремонт серверов
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
order betamethasone 20 gm online cheap – how to get differin without a prescription order monobenzone sale
permethrin order online – buy generic tretinoin cream retin cost
Профессиональный сервисный центр по ремонту сетевых хранилищ в Москве.
Мы предлагаем: ремонт сетевых хранилищ в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр по ремонту сигвеев в Москве.
Мы предлагаем: надежный сервис ремонта сигвеев
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Сервисный центр предлагает ремонт hp probook 455 g1 в москве ремонт hp probook 455 g1 цены
Профессиональный сервисный центр по ремонту автомагнитол в Москве.
Мы предлагаем: сервис центр ремонта магнитол
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
вывод из запоя ростовская область https://www.vyvod-iz-zapoya-rostov15.ru .
принудительный вывод из запоя ростов принудительный вывод из запоя ростов .
Профессиональный сервисный центр по ремонту планшетов в Москве.
Мы предлагаем: ремонт планшетов в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
вывод из запоя в ростове на дону вывод из запоя в ростове на дону .
вызов нарколога на дом круглосуточно https://narkolog-na-dom-krasnodar15.ru .
В магазине сейфов предлагают купить сейф москва сейфы простые
nhà cái
Nếu bạn là một người đam mê cá cược và yêu thích sự hấp dẫn của những con số, thì sảnh lô đề RGbet chính là điểm đến lý tưởng cho bạn. Tôi đã có cơ hội trải nghiệm tại đây và muốn chia sẻ một số ấn tượng cũng như kinh nghiệm của mình.
RGbet nổi bật với mức tỷ lệ trả thưởng cực kỳ hấp dẫn. Trong quá trình chơi, tôi nhận thấy rằng nhà cái này không chỉ cung cấp nhiều loại hình cược mà còn có những mức cược linh hoạt, phù hợp với mọi nhu cầu của người chơi. Bạn có thể bắt đầu với số tiền nhỏ và dần dần tăng lên khi đã nắm bắt được các quy luật và cách thức hoạt động của trò chơi. Sự đa dạng trong các tùy chọn cược giúp cho trải nghiệm chơi không bị nhàm chán, từ cược lô, đề đến các loại cược khác.
Giao diện của RGbet rất thân thiện, dễ dàng điều hướng. Ngay cả khi bạn là người mới, bạn vẫn có thể nhanh chóng tìm thấy những thông tin cần thiết và bắt đầu đặt cược chỉ trong vài phút. Tôi đặc biệt ấn tượng với hệ thống đổi thưởng siêu tốc của nhà cái. Sau khi trúng thưởng, quá trình rút tiền diễn ra rất nhanh chóng và minh bạch. Tôi đã nhận được tiền thưởng trong tài khoản của mình chỉ sau vài phút, điều này thực sự tạo cảm giác yên tâm và tin tưởng cho người chơi.
Một điểm đáng chú ý khác là dịch vụ chăm sóc khách hàng của RGbet. Đội ngũ hỗ trợ luôn sẵn sàng 24/7, giúp tôi giải quyết mọi thắc mắc nhanh chóng và hiệu quả. Chỉ cần một tin nhắn, tôi đã có thể nhận được câu trả lời rõ ràng và hữu ích.
Ngoài ra, để tăng cơ hội trúng thưởng, tôi cũng muốn chia sẻ một vài mẹo nhỏ. Đầu tiên, hãy luôn theo dõi các thống kê và xu hướng của những con số để đưa ra quyết định cược hợp lý. Thứ hai, hãy đặt ra ngân sách cho mỗi lần chơi để tránh việc chi tiêu quá đà. Cuối cùng, đừng quên tham gia các chương trình khuyến mãi và ưu đãi mà RGbet thường xuyên tổ chức; đây là cơ hội tuyệt vời để gia tăng cơ hội thắng lớn.
Tóm lại, RGbet thực sự là một nhà cái lô đề uy tín với nhiều lợi thế vượt trội. Nếu bạn đang tìm kiếm một sân chơi lô đề an toàn, hấp dẫn và đổi thưởng nhanh chóng, đừng ngần ngại tham gia ngay hôm nay! Chắc chắn rằng bạn sẽ có những trải nghiệm thú vị và có cơ hội trúng thưởng lớn tại đây.
Профессиональный сервисный центр по ремонту электросамокатов в Москве.
Мы предлагаем: ремонт электросамокатов на дому с выездом мастера
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
вывод из запоя ростовская область http://www.vyvod-iz-zapoya-rostov17.ru .
rgbet
RGBET: Trang Chủ Cá Cược Uy Tín và Đa Dạng Tại Việt Nam
RGBET đã khẳng định vị thế của mình là một trong những nhà cái hàng đầu tại châu Á và Việt Nam, với đa dạng các dịch vụ cá cược và trò chơi hấp dẫn. Nhà cái này nổi tiếng với việc cung cấp môi trường cá cược an toàn, uy tín và luôn mang lại trải nghiệm tuyệt vời cho người chơi.
Các Loại Hình Cá Cược Tại RGBET
RGBET cung cấp các loại hình cá cược phong phú bao gồm:
Bắn Cá: Một trò chơi đầy kịch tính và thú vị, phù hợp với những người chơi muốn thử thách khả năng săn bắn và nhận về những phần thưởng giá trị.
Thể Thao: Nơi người chơi có thể tham gia đặt cược vào các trận đấu thể thao đa dạng, từ bóng đá, bóng rổ, đến các sự kiện thể thao quốc tế với tỷ lệ cược hấp dẫn.
Game Bài: Đây là một sân chơi dành cho những ai yêu thích các trò chơi bài như tiến lên miền Nam, phỏm, xì dách, và mậu binh. Các trò chơi được phát triển kỹ lưỡng, đem lại cảm giác chân thực và thú vị.
Nổ Hũ: Trò chơi slot với cơ hội trúng Jackpot cực lớn, luôn thu hút sự chú ý của người chơi. Nổ Hũ RGBET là sân chơi hoàn hảo cho những ai muốn thử vận may và giành lấy những phần thưởng khủng.
Lô Đề: Với tỷ lệ trả thưởng cao và nhiều tùy chọn cược, RGBET là nơi lý tưởng cho những người đam mê lô đề.
Tính Năng Nổi Bật Của RGBET
Một trong những điểm nổi bật của RGBET là giao diện thân thiện, dễ sử dụng và hệ thống bảo mật tiên tiến giúp bảo vệ thông tin người chơi. Ngoài ra, nhà cái này còn hỗ trợ các hình thức nạp rút tiền tiện lợi thông qua nhiều kênh khác nhau như OVO, Gopay, Dana, và các chuỗi cửa hàng như Indomaret và Alfamart.
Khuyến Mãi và Dịch Vụ Chăm Sóc Khách Hàng
RGBET không chỉ nổi bật với các trò chơi đa dạng, mà còn cung cấp nhiều chương trình khuyến mãi hấp dẫn như bonus chào mừng, cashback, và các phần thưởng hàng ngày. Đặc biệt, dịch vụ chăm sóc khách hàng của RGBET hoạt động 24/7 với đội ngũ chuyên nghiệp, sẵn sàng hỗ trợ người chơi qua nhiều kênh liên lạc.
Kết Luận
Với những ưu điểm nổi bật về dịch vụ, bảo mật, và trải nghiệm người dùng, RGBET xứng đáng là nhà cái hàng đầu mà người chơi nên lựa chọn khi tham gia vào thế giới cá cược trực tuyến.
Профессиональный сервисный центр сколько стоит ремонт телефона ремонт телефонов цены
rgbet
Trong bối cảnh ngành công nghiệp cá cược trực tuyến ngày càng phát triển, việc lựa chọn một nhà cái uy tín trở nên vô cùng quan trọng đối với những người đam mê cá cược.Nhà cái RGBET nổi lên như một sự lựa chọn hàng đầu đáng để bạn quan tâm, hứa hẹn mang đến cho bạn một trải nghiệm cá cược an toàn, công bằng và thú vị. Từ các trò chơi cá cược đa dạng, dịch vụ chăm sóc khách hàng tận tình đến tỷ lệ cược cạnh tranh, Rgbet sở hữu nhiều ưu điểm vượt trội khiến bạn không thể bỏ qua.Hãy cùng khám phá những lý do tại sao bạn cần quan tâm đến nhà cái Rgbet và tại sao đây nên là lựa chọn hàng đầu của bạn trong thế giới cá cược trực tuyến.
rgbet
RGBET đã nhanh chóng khẳng định vị trí của mình trong ngành công nghiệp cá cược trực tuyến, trở thành một trong những nhà cái hàng đầu đáng để người chơi quan tâm. Dưới đây là một số lý do tại sao RGBET lại nổi bật và trở thành lựa chọn lý tưởng cho những ai đam mê cá cược:
1. Sự Đa Dạng Về Trò Chơi
RGBET cung cấp một loạt các trò chơi cá cược đa dạng, từ cá cược thể thao, casino trực tuyến, đến các trò chơi như slots, poker và các game bài phổ biến. Điều này mang lại cho người chơi nhiều lựa chọn để giải trí và tận hưởng niềm vui khi tham gia cá cược.
2. Dịch Vụ Khách Hàng Chuyên Nghiệp
Một trong những điểm mạnh của RGBET là dịch vụ chăm sóc khách hàng chu đáo, hỗ trợ người chơi 24/7. Bất kể thời gian hay vấn đề gì phát sinh, người chơi luôn có thể nhận được sự hỗ trợ kịp thời, giúp giải quyết các thắc mắc và đảm bảo trải nghiệm cá cược suôn sẻ.
3. Tỷ Lệ Cược Cạnh Tranh
RGBET nổi tiếng với việc cung cấp tỷ lệ cược vô cùng hấp dẫn và cạnh tranh, giúp người chơi có thêm cơ hội thắng lớn. Điều này là điểm hấp dẫn đối với những ai muốn tìm kiếm giá trị tốt nhất từ các khoản cược của mình.
4. Sự Công Bằng và An Toàn
RGBET cam kết mang đến cho người chơi môi trường cá cược minh bạch và an toàn. Hệ thống bảo mật cao cấp đảm bảo rằng thông tin cá nhân và tài khoản của người chơi luôn được bảo vệ.
5. Ưu Đãi và Khuyến Mại
RGBET thường xuyên tung ra các chương trình khuyến mại và ưu đãi đặc biệt dành cho cả người chơi mới và người chơi lâu năm. Đây là một cách tuyệt vời để người chơi có thêm động lực tham gia và tận hưởng nhiều phần thưởng giá trị.
Kết Luận
Nếu bạn đang tìm kiếm một nhà cái uy tín với dịch vụ chuyên nghiệp, trò chơi đa dạng và môi trường cá cược an toàn, RGBET là sự lựa chọn hoàn hảo. Với các ưu điểm vượt trội và những cam kết về chất lượng, RGBET hứa hẹn sẽ mang đến cho bạn những trải nghiệm cá cược trực tuyến đáng nhớ.
В магазине сейфов предлагают взломостойкий сейф 2 класса сейфы второго класса
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: ремонт бытовой техники в волгограде
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
rgbet
rgbet
Тут делают продвижение seo медицинских сайтов seo. медицинских. сайтов
Тут делают продвижение создание сайта под ключ для медицинского учреждения создание сайта клиники
sexy sex sexy sex .
вывод из запоя цена краснодар вывод из запоя цена краснодар .
anonymous viewing of instagram stories anonymous viewing of instagram stories .
нарколог на дом срочно нарколог на дом срочно .
вызов нарколога на дом цена вызов нарколога на дом цена .
В магазине сейфов предлагают взломостойкие сейфы цена взломостойкий сейф
Nếu bạn là một người đam mê cá cược và yêu thích sự hấp dẫn của những con số, thì sảnh lô đề RGbet chính là điểm đến lý tưởng cho bạn. Tôi đã có cơ hội trải nghiệm tại đây và muốn chia sẻ một số ấn tượng cũng như kinh nghiệm của mình.
RGbet nổi bật với mức tỷ lệ trả thưởng cực kỳ hấp dẫn. Trong quá trình chơi, tôi nhận thấy rằng nhà cái này không chỉ cung cấp nhiều loại hình cược mà còn có những mức cược linh hoạt, phù hợp với mọi nhu cầu của người chơi. Bạn có thể bắt đầu với số tiền nhỏ và dần dần tăng lên khi đã nắm bắt được các quy luật và cách thức hoạt động của trò chơi. Sự đa dạng trong các tùy chọn cược giúp cho trải nghiệm chơi không bị nhàm chán, từ cược lô, đề đến các loại cược khác.
Giao diện của RGbet rất thân thiện, dễ dàng điều hướng. Ngay cả khi bạn là người mới, bạn vẫn có thể nhanh chóng tìm thấy những thông tin cần thiết và bắt đầu đặt cược chỉ trong vài phút. Tôi đặc biệt ấn tượng với hệ thống đổi thưởng siêu tốc của nhà cái. Sau khi trúng thưởng, quá trình rút tiền diễn ra rất nhanh chóng và minh bạch. Tôi đã nhận được tiền thưởng trong tài khoản của mình chỉ sau vài phút, điều này thực sự tạo cảm giác yên tâm và tin tưởng cho người chơi.
Một điểm đáng chú ý khác là dịch vụ chăm sóc khách hàng của RGbet. Đội ngũ hỗ trợ luôn sẵn sàng 24/7, giúp tôi giải quyết mọi thắc mắc nhanh chóng và hiệu quả. Chỉ cần một tin nhắn, tôi đã có thể nhận được câu trả lời rõ ràng và hữu ích.
Ngoài ra, để tăng cơ hội trúng thưởng, tôi cũng muốn chia sẻ một vài mẹo nhỏ. Đầu tiên, hãy luôn theo dõi các thống kê và xu hướng của những con số để đưa ra quyết định cược hợp lý. Thứ hai, hãy đặt ra ngân sách cho mỗi lần chơi để tránh việc chi tiêu quá đà. Cuối cùng, đừng quên tham gia các chương trình khuyến mãi và ưu đãi mà RGbet thường xuyên tổ chức; đây là cơ hội tuyệt vời để gia tăng cơ hội thắng lớn.
Tóm lại, RGbet thực sự là một nhà cái lô đề uy tín với nhiều lợi thế vượt trội. Nếu bạn đang tìm kiếm một sân chơi lô đề an toàn, hấp dẫn và đổi thưởng nhanh chóng, đừng ngần ngại tham gia ngay hôm nay! Chắc chắn rằng bạn sẽ có những trải nghiệm thú vị và có cơ hội trúng thưởng lớn tại đây.
DJ88 adalah situs game deposit pulsa terbaik di Indonesia yang menawarkan pengalaman bermain game online yang lengkap dan mudah. Hanya dengan satu ID, pemain dapat mengakses berbagai jenis permainan yang tersedia di platform ini, memberikan kenyamanan dan variasi permainan yang tak tertandingi.
Sebagai situs game online berlisensi resmi dari PAGCOR (Philippine Amusement and Gaming Corporation), DJ88 menjamin keamanan dan kenyamanan para penggunanya. Dengan dukungan server hosting yang cepat serta sistem keamanan canggih berbasis enkripsi terkini, DJ88 memberikan rasa aman dalam menjaga privasi dan data penggunanya. Tampilan situs yang modern dan intuitif juga memastikan pengalaman bermain yang menyenangkan dan mudah diakses oleh semua kalangan.
Salah satu keunggulan DJ88 adalah kemudahan dalam melakukan deposit pulsa, baik melalui XL maupun Telkomsel, dengan potongan yang lebih rendah dibandingkan situs lainnya. Hal ini menjadikan DJ88 sebagai salah satu situs game online pulsa terbesar di Indonesia. Tidak hanya itu, pengguna juga dapat melakukan deposit melalui berbagai platform E-commerce resmi seperti OVO, Gopay, Dana, atau bahkan melalui minimarket seperti Indomaret dan Alfamart.
DJ88 dikenal sebagai agen game online terpercaya yang selalu menempatkan kepercayaan pengguna sebagai prioritas utama. Dengan berbagai upaya menjaga reputasi dan memberikan layanan terbaik, DJ88 telah menjadi pilihan utama bagi pemain game online di Indonesia.
Platform ini menawarkan berbagai macam permainan online yang dapat diakses kapan saja dan di mana saja, tanpa perlu repot bepergian. DJ88 juga menyediakan game live dengan host cantik yang berinteraksi secara real-time melalui kamera, memberikan pengalaman bermain yang lebih menarik dan interaktif.
Selain pilihan permainan yang beragam, DJ88 juga menyediakan berbagai promo menarik seperti welcome bonus 20%, bonus deposit harian, hingga cashback, yang tentunya menambah keseruan bermain. Promo ini dirancang agar pemain dapat menikmati keuntungan lebih dari setiap permainan.
DJ88 juga unggul dalam layanan pelanggan. Dengan tim customer service yang profesional, ramah, dan siap membantu 24 jam non-stop melalui berbagai platform seperti Live Chat, WhatsApp, dan media sosial, DJ88 memastikan setiap pertanyaan dan masalah pengguna dapat diselesaikan dengan cepat dan tepat.
Dengan segala keunggulan yang ditawarkan, DJ88 menjadi situs game online pulsa pilihan terbaik di Indonesia. Bergabunglah sekarang dan nikmati berbagai keuntungan dari DJ88!
RGBET: Trang Chủ Cá Cược Uy Tín và Đa Dạng Tại Việt Nam
RGBET đã khẳng định vị thế của mình là một trong những nhà cái hàng đầu tại châu Á và Việt Nam, với đa dạng các dịch vụ cá cược và trò chơi hấp dẫn. Nhà cái này nổi tiếng với việc cung cấp môi trường cá cược an toàn, uy tín và luôn mang lại trải nghiệm tuyệt vời cho người chơi.
Các Loại Hình Cá Cược Tại RGBET
RGBET cung cấp các loại hình cá cược phong phú bao gồm:
Bắn Cá: Một trò chơi đầy kịch tính và thú vị, phù hợp với những người chơi muốn thử thách khả năng săn bắn và nhận về những phần thưởng giá trị.
Thể Thao: Nơi người chơi có thể tham gia đặt cược vào các trận đấu thể thao đa dạng, từ bóng đá, bóng rổ, đến các sự kiện thể thao quốc tế với tỷ lệ cược hấp dẫn.
Game Bài: Đây là một sân chơi dành cho những ai yêu thích các trò chơi bài như tiến lên miền Nam, phỏm, xì dách, và mậu binh. Các trò chơi được phát triển kỹ lưỡng, đem lại cảm giác chân thực và thú vị.
Nổ Hũ: Trò chơi slot với cơ hội trúng Jackpot cực lớn, luôn thu hút sự chú ý của người chơi. Nổ Hũ RGBET là sân chơi hoàn hảo cho những ai muốn thử vận may và giành lấy những phần thưởng khủng.
Lô Đề: Với tỷ lệ trả thưởng cao và nhiều tùy chọn cược, RGBET là nơi lý tưởng cho những người đam mê lô đề.
Tính Năng Nổi Bật Của RGBET
Một trong những điểm nổi bật của RGBET là giao diện thân thiện, dễ sử dụng và hệ thống bảo mật tiên tiến giúp bảo vệ thông tin người chơi. Ngoài ra, nhà cái này còn hỗ trợ các hình thức nạp rút tiền tiện lợi thông qua nhiều kênh khác nhau như OVO, Gopay, Dana, và các chuỗi cửa hàng như Indomaret và Alfamart.
Khuyến Mãi và Dịch Vụ Chăm Sóc Khách Hàng
RGBET không chỉ nổi bật với các trò chơi đa dạng, mà còn cung cấp nhiều chương trình khuyến mãi hấp dẫn như bonus chào mừng, cashback, và các phần thưởng hàng ngày. Đặc biệt, dịch vụ chăm sóc khách hàng của RGBET hoạt động 24/7 với đội ngũ chuyên nghiệp, sẵn sàng hỗ trợ người chơi qua nhiều kênh liên lạc.
Kết Luận
Với những ưu điểm nổi bật về dịch vụ, bảo mật, và trải nghiệm người dùng, RGBET xứng đáng là nhà cái hàng đầu mà người chơi nên lựa chọn khi tham gia vào thế giới cá cược trực tuyến.
Тут делают продвижение медицинский seo seo медицинских сайтов
Тут делают продвижение разработка мед сайтов создание сайта для клиники
Trong bối cảnh ngành công nghiệp cá cược trực tuyến ngày càng phát triển, việc lựa chọn một nhà cái uy tín trở nên vô cùng quan trọng đối với những người đam mê cá cược.Nhà cái RGBET nổi lên như một sự lựa chọn hàng đầu đáng để bạn quan tâm, hứa hẹn mang đến cho bạn một trải nghiệm cá cược an toàn, công bằng và thú vị. Từ các trò chơi cá cược đa dạng, dịch vụ chăm sóc khách hàng tận tình đến tỷ lệ cược cạnh tranh, Rgbet sở hữu nhiều ưu điểm vượt trội khiến bạn không thể bỏ qua.Hãy cùng khám phá những lý do tại sao bạn cần quan tâm đến nhà cái Rgbet và tại sao đây nên là lựa chọn hàng đầu của bạn trong thế giới cá cược trực tuyến.
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервис центры бытовой техники воронеж
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Профессиональный сервисный центр ремонт телефонов москва рядом ремонт платы телефона
metronidazole over the counter – buy cenforce 50mg generic cenforce 50mg price
Тут делают продвижение seo медицинских сайтов seo медицинских сайтов
Тут делают продвижение разработка медицинского сайта разработка медицинских сайтов
Тут делают продвижение разработка медицинского сайта разработка медицинских сайтов
rgbet
Nếu bạn là một người đam mê cá cược và yêu thích sự hấp dẫn của những con số, thì sảnh lô đề RGbet chính là điểm đến lý tưởng cho bạn. Tôi đã có cơ hội trải nghiệm tại đây và muốn chia sẻ một số ấn tượng cũng như kinh nghiệm của mình.
RGbet nổi bật với mức tỷ lệ trả thưởng cực kỳ hấp dẫn. Trong quá trình chơi, tôi nhận thấy rằng nhà cái này không chỉ cung cấp nhiều loại hình cược mà còn có những mức cược linh hoạt, phù hợp với mọi nhu cầu của người chơi. Bạn có thể bắt đầu với số tiền nhỏ và dần dần tăng lên khi đã nắm bắt được các quy luật và cách thức hoạt động của trò chơi. Sự đa dạng trong các tùy chọn cược giúp cho trải nghiệm chơi không bị nhàm chán, từ cược lô, đề đến các loại cược khác.
Giao diện của RGbet rất thân thiện, dễ dàng điều hướng. Ngay cả khi bạn là người mới, bạn vẫn có thể nhanh chóng tìm thấy những thông tin cần thiết và bắt đầu đặt cược chỉ trong vài phút. Tôi đặc biệt ấn tượng với hệ thống đổi thưởng siêu tốc của nhà cái. Sau khi trúng thưởng, quá trình rút tiền diễn ra rất nhanh chóng và minh bạch. Tôi đã nhận được tiền thưởng trong tài khoản của mình chỉ sau vài phút, điều này thực sự tạo cảm giác yên tâm và tin tưởng cho người chơi.
Một điểm đáng chú ý khác là dịch vụ chăm sóc khách hàng của RGbet. Đội ngũ hỗ trợ luôn sẵn sàng 24/7, giúp tôi giải quyết mọi thắc mắc nhanh chóng và hiệu quả. Chỉ cần một tin nhắn, tôi đã có thể nhận được câu trả lời rõ ràng và hữu ích.
Ngoài ra, để tăng cơ hội trúng thưởng, tôi cũng muốn chia sẻ một vài mẹo nhỏ. Đầu tiên, hãy luôn theo dõi các thống kê và xu hướng của những con số để đưa ra quyết định cược hợp lý. Thứ hai, hãy đặt ra ngân sách cho mỗi lần chơi để tránh việc chi tiêu quá đà. Cuối cùng, đừng quên tham gia các chương trình khuyến mãi và ưu đãi mà RGbet thường xuyên tổ chức; đây là cơ hội tuyệt vời để gia tăng cơ hội thắng lớn.
Tóm lại, RGbet thực sự là một nhà cái lô đề uy tín với nhiều lợi thế vượt trội. Nếu bạn đang tìm kiếm một sân chơi lô đề an toàn, hấp dẫn và đổi thưởng nhanh chóng, đừng ngần ngại tham gia ngay hôm nay! Chắc chắn rằng bạn sẽ có những trải nghiệm thú vị và có cơ hội trúng thưởng lớn tại đây.
Профессиональный сервисный центр по ремонту моноблоков iMac в Москве.
Мы предлагаем: ремонт imac москва
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
RGBET: Trang Chủ Cá Cược Uy Tín và Đa Dạng Tại Việt Nam
RGBET đã khẳng định vị thế của mình là một trong những nhà cái hàng đầu tại châu Á và Việt Nam, với đa dạng các dịch vụ cá cược và trò chơi hấp dẫn. Nhà cái này nổi tiếng với việc cung cấp môi trường cá cược an toàn, uy tín và luôn mang lại trải nghiệm tuyệt vời cho người chơi.
Các Loại Hình Cá Cược Tại RGBET
RGBET cung cấp các loại hình cá cược phong phú bao gồm:
Bắn Cá: Một trò chơi đầy kịch tính và thú vị, phù hợp với những người chơi muốn thử thách khả năng săn bắn và nhận về những phần thưởng giá trị.
Thể Thao: Nơi người chơi có thể tham gia đặt cược vào các trận đấu thể thao đa dạng, từ bóng đá, bóng rổ, đến các sự kiện thể thao quốc tế với tỷ lệ cược hấp dẫn.
Game Bài: Đây là một sân chơi dành cho những ai yêu thích các trò chơi bài như tiến lên miền Nam, phỏm, xì dách, và mậu binh. Các trò chơi được phát triển kỹ lưỡng, đem lại cảm giác chân thực và thú vị.
Nổ Hũ: Trò chơi slot với cơ hội trúng Jackpot cực lớn, luôn thu hút sự chú ý của người chơi. Nổ Hũ RGBET là sân chơi hoàn hảo cho những ai muốn thử vận may và giành lấy những phần thưởng khủng.
Lô Đề: Với tỷ lệ trả thưởng cao và nhiều tùy chọn cược, RGBET là nơi lý tưởng cho những người đam mê lô đề.
Tính Năng Nổi Bật Của RGBET
Một trong những điểm nổi bật của RGBET là giao diện thân thiện, dễ sử dụng và hệ thống bảo mật tiên tiến giúp bảo vệ thông tin người chơi. Ngoài ra, nhà cái này còn hỗ trợ các hình thức nạp rút tiền tiện lợi thông qua nhiều kênh khác nhau như OVO, Gopay, Dana, và các chuỗi cửa hàng như Indomaret và Alfamart.
Khuyến Mãi và Dịch Vụ Chăm Sóc Khách Hàng
RGBET không chỉ nổi bật với các trò chơi đa dạng, mà còn cung cấp nhiều chương trình khuyến mãi hấp dẫn như bonus chào mừng, cashback, và các phần thưởng hàng ngày. Đặc biệt, dịch vụ chăm sóc khách hàng của RGBET hoạt động 24/7 với đội ngũ chuyên nghiệp, sẵn sàng hỗ trợ người chơi qua nhiều kênh liên lạc.
Kết Luận
Với những ưu điểm nổi bật về dịch vụ, bảo mật, và trải nghiệm người dùng, RGBET xứng đáng là nhà cái hàng đầu mà người chơi nên lựa chọn khi tham gia vào thế giới cá cược trực tuyến.
free sx movies free sx movies .
как вывести из запоя против воли как вывести из запоя против воли .
ST666 – Trang Chủ Cá Cược Chính Thức Tại Việt Nam
ST666 là một trong những nhà cái cá cược hàng đầu châu Á, nổi bật với dịch vụ đa dạng và hệ thống game đổi thưởng hấp dẫn. Với nhiều năm kinh nghiệm trong lĩnh vực cá cược trực tuyến, ST666 đã xây dựng được uy tín và niềm tin từ hàng triệu người chơi trên khắp khu vực.
Hệ Thống Game Đổi Thưởng ST666
Tại ST666, người chơi có thể trải nghiệm nhiều loại hình giải trí khác nhau, bao gồm:
Bắn cá: Một trong những trò chơi được ưa chuộng nhất, mang lại trải nghiệm bắn súng dưới nước độc đáo và hấp dẫn.
Thể thao: Cung cấp cược thể thao từ các giải đấu lớn nhỏ trên toàn thế giới với tỷ lệ cược hấp dẫn.
Xổ số: Trò chơi đơn giản, dễ chơi với cơ hội nhận thưởng lớn.
Game bài: Đa dạng các trò chơi bài như poker, baccarat, và nhiều thể loại khác.
Nổ hũ: Trò chơi đầy kịch tính với các phần thưởng cực lớn.
Live Casino: Người chơi có thể tham gia các sòng bài trực tuyến với dealer thật qua hình thức phát trực tiếp, mang lại cảm giác như đang ngồi tại sòng bài thực sự.
Giao Diện Hiện Đại & Bảo Mật Tuyệt Đối
ST666 không chỉ nổi bật với hệ thống game phong phú mà còn thu hút người chơi nhờ vào giao diện hiện đại, thân thiện. Thiết kế trang web đẹp mắt, dễ sử dụng giúp người chơi dễ dàng thao tác và tận hưởng các trò chơi mà không gặp khó khăn.
Đặc biệt, hệ thống bảo mật của ST666 luôn được đánh giá cao. Tất cả các giao dịch và thông tin cá nhân của người chơi đều được bảo vệ bằng công nghệ mã hóa tiên tiến, đảm bảo an toàn tuyệt đối cho người dùng.
Ưu Đãi Hấp Dẫn & Tỷ Lệ Đổi Thưởng Cao
ST666 luôn mang đến cho người chơi nhiều khuyến mãi hấp dẫn. Người chơi có thể nhận được 280k miễn phí khi đăng nhập hàng ngày, cùng với hàng loạt các chương trình ưu đãi khác, như thưởng nạp đầu, khuyến mãi hoàn tiền, và nhiều sự kiện đặc biệt dành cho các thành viên thân thiết.
Bên cạnh đó, tỷ lệ đổi thưởng tại ST666 luôn cao hơn so với nhiều nhà cái khác, mang lại cơ hội thắng lớn cho người chơi.
Tải App ST666
Để thuận tiện hơn trong việc trải nghiệm, ST666 đã phát triển ứng dụng dành riêng cho di động. Người chơi có thể dễ dàng tải app ST666 về máy và tham gia cá cược bất cứ lúc nào, bất cứ nơi đâu, mà không cần phải truy cập qua trình duyệt web.
Kết Luận
ST666 là lựa chọn lý tưởng cho những ai yêu thích cá cược và muốn tìm kiếm một nhà cái đáng tin cậy. Với hệ thống game đa dạng, giao diện hiện đại, bảo mật tốt và nhiều khuyến mãi hấp dẫn, ST666 chắc chắn sẽ mang lại cho người chơi những trải nghiệm tuyệt vời và đáng nhớ.
Câu lạc bộ bóng đá AS Roma
ST666 tự hào là đối tác tài trợ hàng đầu của câu lạc bộ bóng đá AS Roma – một biểu tượng vĩ đại trong làng bóng đá Ý. AS Roma không chỉ là đội bóng nổi tiếng với lịch sử thi đấu ấn tượng mà còn là đối tác quan trọng trong các hợp đồng hợp tác với ST666. Với sự hợp tác này, AS Roma đã hỗ trợ nhà cái ST666 thông qua những khoản đầu tư triệu đô, giúp phát triển mạnh mẽ mảng thể thao trực tuyến và mở ra cơ hội lớn cho người chơi cá cược tại thị trường quốc tế.
Câu lạc bộ bóng đá Bayern Munich
ST666 cũng vinh dự là nhà tài trợ hàng đầu của câu lạc bộ bóng đá Bayern Munich – một đội bóng nổi tiếng không chỉ ở Đức mà còn trên toàn thế giới. Với lịch sử vô địch lẫy lừng và sự thống trị tại các giải đấu quốc tế, Bayern Munich đã trở thành biểu tượng lớn trong lòng người hâm mộ. Sự hợp tác giữa ST666 và Bayern Munich không chỉ dừng lại ở việc tài trợ mà còn góp phần nâng cao trải nghiệm của người chơi thông qua cải tiến hệ thống giao dịch tài chính, giúp quy trình nạp rút tiền của bet thủ trở nên thuận tiện và nhanh chóng hơn.
Câu lạc bộ bóng đá Porto
Không thể không nhắc đến câu lạc bộ bóng đá Porto, nơi ST666 hân hạnh trở thành đối tác tài trợ hàng đầu. Porto không chỉ là biểu tượng của sự sáng tạo và thành công trong làng bóng đá Bồ Đào Nha mà còn hỗ trợ ST666 trong các thủ tục xin giấy phép và chứng nhận tại châu Âu và Philippines. Sự hợp tác này đã mang lại giá trị lớn cho ST666 khi mở rộng quy mô hoạt động ra nhiều khu vực và thị trường mới.
Câu lạc bộ bóng đá Arsenal
Trong làng bóng đá Anh, câu lạc bộ bóng đá Arsenal là biểu tượng của sự tinh tế và phong cách. ST666 rất tự hào khi trở thành nhà tài trợ chính của Arsenal, giúp nhà cái này không chỉ nâng cao vị thế mà còn mở rộng thị trường cá cược bóng đá toàn cầu. Arsenal đã đóng vai trò quan trọng trong việc hỗ trợ ST666 phát triển hệ thống cá cược, từ đó mang lại trải nghiệm tốt nhất cho người chơi.
Câu lạc bộ bóng đá Sevilla
Cuối cùng, câu lạc bộ bóng đá Sevilla – biểu tượng của sự khát vọng và thành công trong bóng đá Tây Ban Nha, cũng đã trở thành đối tác quan trọng của ST666. Sevilla không chỉ góp phần thúc đẩy ST666 về mặt thương mại mà còn cung cấp công nghệ bảo mật hàng đầu, đảm bảo rằng thông tin cá nhân, tài khoản và các giao dịch của người chơi đều được bảo vệ một cách tối ưu.
Điểm vượt trội của ST666 so với các đối thủ cạnh tranh khác
Sự hợp tác chiến lược giữa ST666 và các câu lạc bộ bóng đá hàng đầu không chỉ nâng cao vị thế của ST666 trên thị trường, mà còn mang lại những lợi ích vượt trội cho người chơi. Những điểm mạnh này bao gồm:
Hệ thống bảo mật tiên tiến: ST666 đã được Sevilla hỗ trợ trong việc nâng cấp công nghệ bảo mật, đảm bảo mọi giao dịch và thông tin người dùng đều an toàn.
Hệ thống nạp rút tiện lợi: Sự hợp tác với Bayern Munich giúp ST666 cải tiến hệ thống giao dịch tài chính, mang lại trải nghiệm nạp rút nhanh chóng và hiệu quả cho người chơi.
Mở rộng thị trường và dịch vụ: Nhờ sự hỗ trợ từ Arsenal và AS Roma, ST666 đã thành công trong việc mở rộng hệ thống cá cược bóng đá và tiếp cận thêm nhiều người chơi trên toàn thế giới.
ST666 không chỉ là một nhà cái hàng đầu mà còn là một đối tác đáng tin cậy của các câu lạc bộ bóng đá danh tiếng, luôn cam kết mang lại dịch vụ tốt nhất và trải nghiệm tối ưu cho người chơi.
вывод из запоя на дому вывод из запоя на дому .
property for rent in nigeria
We are a leading real estate consultancy company in Nigeria. Our integrated real estate services include facility management, portfolio management, real estate consultancy, property management, office renovation, property sales and rental, interior design, office decoration, real estate turnkey project, property refurbishment and sales.
st666 bóng đá
Câu lạc bộ bóng đá AS Roma
ST666 tự hào là đối tác tài trợ hàng đầu của câu lạc bộ bóng đá AS Roma – một biểu tượng vĩ đại trong làng bóng đá Ý. AS Roma không chỉ là đội bóng nổi tiếng với lịch sử thi đấu ấn tượng mà còn là đối tác quan trọng trong các hợp đồng hợp tác với ST666. Với sự hợp tác này, AS Roma đã hỗ trợ nhà cái ST666 thông qua những khoản đầu tư triệu đô, giúp phát triển mạnh mẽ mảng thể thao trực tuyến và mở ra cơ hội lớn cho người chơi cá cược tại thị trường quốc tế.
Câu lạc bộ bóng đá Bayern Munich
ST666 cũng vinh dự là nhà tài trợ hàng đầu của câu lạc bộ bóng đá Bayern Munich – một đội bóng nổi tiếng không chỉ ở Đức mà còn trên toàn thế giới. Với lịch sử vô địch lẫy lừng và sự thống trị tại các giải đấu quốc tế, Bayern Munich đã trở thành biểu tượng lớn trong lòng người hâm mộ. Sự hợp tác giữa ST666 và Bayern Munich không chỉ dừng lại ở việc tài trợ mà còn góp phần nâng cao trải nghiệm của người chơi thông qua cải tiến hệ thống giao dịch tài chính, giúp quy trình nạp rút tiền của bet thủ trở nên thuận tiện và nhanh chóng hơn.
Câu lạc bộ bóng đá Porto
Không thể không nhắc đến câu lạc bộ bóng đá Porto, nơi ST666 hân hạnh trở thành đối tác tài trợ hàng đầu. Porto không chỉ là biểu tượng của sự sáng tạo và thành công trong làng bóng đá Bồ Đào Nha mà còn hỗ trợ ST666 trong các thủ tục xin giấy phép và chứng nhận tại châu Âu và Philippines. Sự hợp tác này đã mang lại giá trị lớn cho ST666 khi mở rộng quy mô hoạt động ra nhiều khu vực và thị trường mới.
Câu lạc bộ bóng đá Arsenal
Trong làng bóng đá Anh, câu lạc bộ bóng đá Arsenal là biểu tượng của sự tinh tế và phong cách. ST666 rất tự hào khi trở thành nhà tài trợ chính của Arsenal, giúp nhà cái này không chỉ nâng cao vị thế mà còn mở rộng thị trường cá cược bóng đá toàn cầu. Arsenal đã đóng vai trò quan trọng trong việc hỗ trợ ST666 phát triển hệ thống cá cược, từ đó mang lại trải nghiệm tốt nhất cho người chơi.
Câu lạc bộ bóng đá Sevilla
Cuối cùng, câu lạc bộ bóng đá Sevilla – biểu tượng của sự khát vọng và thành công trong bóng đá Tây Ban Nha, cũng đã trở thành đối tác quan trọng của ST666. Sevilla không chỉ góp phần thúc đẩy ST666 về mặt thương mại mà còn cung cấp công nghệ bảo mật hàng đầu, đảm bảo rằng thông tin cá nhân, tài khoản và các giao dịch của người chơi đều được bảo vệ một cách tối ưu.
Điểm vượt trội của ST666 so với các đối thủ cạnh tranh khác
Sự hợp tác chiến lược giữa ST666 và các câu lạc bộ bóng đá hàng đầu không chỉ nâng cao vị thế của ST666 trên thị trường, mà còn mang lại những lợi ích vượt trội cho người chơi. Những điểm mạnh này bao gồm:
Hệ thống bảo mật tiên tiến: ST666 đã được Sevilla hỗ trợ trong việc nâng cấp công nghệ bảo mật, đảm bảo mọi giao dịch và thông tin người dùng đều an toàn.
Hệ thống nạp rút tiện lợi: Sự hợp tác với Bayern Munich giúp ST666 cải tiến hệ thống giao dịch tài chính, mang lại trải nghiệm nạp rút nhanh chóng và hiệu quả cho người chơi.
Mở rộng thị trường và dịch vụ: Nhờ sự hỗ trợ từ Arsenal và AS Roma, ST666 đã thành công trong việc mở rộng hệ thống cá cược bóng đá và tiếp cận thêm nhiều người chơi trên toàn thế giới.
ST666 không chỉ là một nhà cái hàng đầu mà còn là một đối tác đáng tin cậy của các câu lạc bộ bóng đá danh tiếng, luôn cam kết mang lại dịch vụ tốt nhất và trải nghiệm tối ưu cho người chơi.
вывод из запоя на дому краснодар круглосуточно вывод из запоя на дому краснодар круглосуточно .
вывод из запоя цена вывод из запоя цена .
각종 디비 판매
ST666 – Lựa Chọn Hàng Đầu Trong Thế Giới Cá Cược Trực Tuyến
Trong thời đại mà ngành công nghiệp cá cược trực tuyến đang bùng nổ, việc chọn một nhà cái uy tín là yếu tố quan trọng để đảm bảo trải nghiệm chơi an toàn và đáng tin cậy. ST666 nhanh chóng khẳng định vị thế của mình trên thị trường với những dịch vụ chất lượng và hệ thống bảo mật cao cấp, mang lại trải nghiệm cá cược công bằng, thú vị và an toàn.
Hệ Thống Trò Chơi Đa Dạng
ST666 cung cấp một danh mục trò chơi cá cược đa dạng, đáp ứng mọi nhu cầu và sở thích của người chơi. Từ thể thao, bắn cá, game bài, cho đến xổ số và live casino, tất cả đều được tối ưu hóa để mang lại cảm giác hứng thú cho người tham gia. Đặc biệt, với Live Casino, người chơi sẽ được trải nghiệm cá cược với các dealer thật thông qua hình thức phát trực tiếp, tạo cảm giác như đang tham gia tại các sòng bài thực tế.
Tỷ Lệ Cược Cạnh Tranh
Một trong những ưu điểm nổi bật của ST666 chính là tỷ lệ cược cực kỳ cạnh tranh, giúp người chơi tối ưu hóa lợi nhuận của mình. Các trận đấu thể thao được cập nhật liên tục với tỷ lệ cược hấp dẫn, tạo cơ hội chiến thắng lớn cho những ai yêu thích cá cược thể thao.
Bảo Mật An Toàn Tuyệt Đối
Yếu tố bảo mật luôn là một trong những tiêu chí hàng đầu khi chọn nhà cái cá cược. ST666 sử dụng công nghệ mã hóa hiện đại để bảo vệ thông tin cá nhân và các giao dịch tài chính của người chơi, đảm bảo mọi dữ liệu luôn được bảo mật tuyệt đối. Người chơi hoàn toàn có thể yên tâm khi tham gia cá cược tại đây.
Chăm Sóc Khách Hàng Chuyên Nghiệp
Dịch vụ chăm sóc khách hàng của ST666 luôn sẵn sàng hỗ trợ 24/7 qua nhiều kênh khác nhau như Live Chat, WhatsApp, Facebook, đảm bảo giải đáp mọi thắc mắc và xử lý các vấn đề nhanh chóng. Đội ngũ nhân viên tại đây được đào tạo chuyên nghiệp, tận tâm và chu đáo, luôn đặt lợi ích của khách hàng lên hàng đầu.
Ưu Đãi Hấp Dẫn
ST666 không chỉ nổi bật với các sản phẩm cá cược mà còn thu hút người chơi bởi các chương trình khuyến mãi hấp dẫn. Người chơi có thể nhận được nhiều ưu đãi như 280k miễn phí khi đăng nhập hàng ngày, cùng các chương trình thưởng nạp và hoàn tiền liên tục, giúp tối đa hóa cơ hội chiến thắng.
Lý Do ST666 Là Lựa Chọn Hàng Đầu
Sự kết hợp hoàn hảo giữa giao diện hiện đại, hệ thống trò chơi đa dạng, dịch vụ khách hàng tận tâm và tỷ lệ cược cạnh tranh đã giúp ST666 trở thành một trong những nhà cái cá cược trực tuyến uy tín hàng đầu tại Việt Nam. Đối với những ai đang tìm kiếm một nhà cái an toàn và chuyên nghiệp, ST666 chắc chắn sẽ là lựa chọn không thể bỏ qua.
Kết Luận
Với những ưu điểm vượt trội, ST666 xứng đáng là địa chỉ cá cược uy tín và an toàn cho tất cả người chơi. Đăng ký ngay hôm nay để trải nghiệm hệ thống cá cược đẳng cấp và nhận những ưu đãi hấp dẫn từ ST666!
buy augmentin 375mg sale – how to get clavulanate without a prescription order levothroid pills
st666
Nhà cái ST666 được biết đến là sân chơi uy tín cung cấp các sản phẩm trò chơi cực kỳ đa dạng và chất lượng. Số lượng người tham gia vào hệ thống ngày càng tăng cao và chưa có dấu hiệu dừng lại. Hướng dẫn tham gia nhà cái nếu như anh em muốn tìm kiếm cơ hội nhận thưởng khủng. Hãy cùng khám phá những thông tin cần biết tại nhà cái để đặt cược và săn thưởng thành công.
вывод из запоя наркологом http://www.vyvod-iz-zapoya-ekaterinburg16.ru/ .
эко кожа цена эко кожа цена .
ST666 – Lựa Chọn Hàng Đầu Trong Thế Giới Cá Cược Trực Tuyến
Trong thời đại mà ngành công nghiệp cá cược trực tuyến đang bùng nổ, việc chọn một nhà cái uy tín là yếu tố quan trọng để đảm bảo trải nghiệm chơi an toàn và đáng tin cậy. ST666 nhanh chóng khẳng định vị thế của mình trên thị trường với những dịch vụ chất lượng và hệ thống bảo mật cao cấp, mang lại trải nghiệm cá cược công bằng, thú vị và an toàn.
Hệ Thống Trò Chơi Đa Dạng
ST666 cung cấp một danh mục trò chơi cá cược đa dạng, đáp ứng mọi nhu cầu và sở thích của người chơi. Từ thể thao, bắn cá, game bài, cho đến xổ số và live casino, tất cả đều được tối ưu hóa để mang lại cảm giác hứng thú cho người tham gia. Đặc biệt, với Live Casino, người chơi sẽ được trải nghiệm cá cược với các dealer thật thông qua hình thức phát trực tiếp, tạo cảm giác như đang tham gia tại các sòng bài thực tế.
Tỷ Lệ Cược Cạnh Tranh
Một trong những ưu điểm nổi bật của ST666 chính là tỷ lệ cược cực kỳ cạnh tranh, giúp người chơi tối ưu hóa lợi nhuận của mình. Các trận đấu thể thao được cập nhật liên tục với tỷ lệ cược hấp dẫn, tạo cơ hội chiến thắng lớn cho những ai yêu thích cá cược thể thao.
Bảo Mật An Toàn Tuyệt Đối
Yếu tố bảo mật luôn là một trong những tiêu chí hàng đầu khi chọn nhà cái cá cược. ST666 sử dụng công nghệ mã hóa hiện đại để bảo vệ thông tin cá nhân và các giao dịch tài chính của người chơi, đảm bảo mọi dữ liệu luôn được bảo mật tuyệt đối. Người chơi hoàn toàn có thể yên tâm khi tham gia cá cược tại đây.
Chăm Sóc Khách Hàng Chuyên Nghiệp
Dịch vụ chăm sóc khách hàng của ST666 luôn sẵn sàng hỗ trợ 24/7 qua nhiều kênh khác nhau như Live Chat, WhatsApp, Facebook, đảm bảo giải đáp mọi thắc mắc và xử lý các vấn đề nhanh chóng. Đội ngũ nhân viên tại đây được đào tạo chuyên nghiệp, tận tâm và chu đáo, luôn đặt lợi ích của khách hàng lên hàng đầu.
Ưu Đãi Hấp Dẫn
ST666 không chỉ nổi bật với các sản phẩm cá cược mà còn thu hút người chơi bởi các chương trình khuyến mãi hấp dẫn. Người chơi có thể nhận được nhiều ưu đãi như 280k miễn phí khi đăng nhập hàng ngày, cùng các chương trình thưởng nạp và hoàn tiền liên tục, giúp tối đa hóa cơ hội chiến thắng.
Lý Do ST666 Là Lựa Chọn Hàng Đầu
Sự kết hợp hoàn hảo giữa giao diện hiện đại, hệ thống trò chơi đa dạng, dịch vụ khách hàng tận tâm và tỷ lệ cược cạnh tranh đã giúp ST666 trở thành một trong những nhà cái cá cược trực tuyến uy tín hàng đầu tại Việt Nam. Đối với những ai đang tìm kiếm một nhà cái an toàn và chuyên nghiệp, ST666 chắc chắn sẽ là lựa chọn không thể bỏ qua.
Kết Luận
Với những ưu điểm vượt trội, ST666 xứng đáng là địa chỉ cá cược uy tín và an toàn cho tất cả người chơi. Đăng ký ngay hôm nay để trải nghiệm hệ thống cá cược đẳng cấp và nhận những ưu đãi hấp dẫn từ ST666!
сайт вакансий казахстан сайт вакансий казахстан .
работа с ежедневной оплатой алматы для мужчин работа с ежедневной оплатой алматы для мужчин .
магазин сейфов предлагает купить сейф 3 класса сейфы 3 класс взломостойкости
работа в астане с ежедневной оплатой для женщин работа в астане с ежедневной оплатой для женщин .
ST666 – Lựa Chọn Hàng Đầu Trong Thế Giới Cá Cược Trực Tuyến
Trong thời đại mà ngành công nghiệp cá cược trực tuyến đang bùng nổ, việc chọn một nhà cái uy tín là yếu tố quan trọng để đảm bảo trải nghiệm chơi an toàn và đáng tin cậy. ST666 nhanh chóng khẳng định vị thế của mình trên thị trường với những dịch vụ chất lượng và hệ thống bảo mật cao cấp, mang lại trải nghiệm cá cược công bằng, thú vị và an toàn.
Hệ Thống Trò Chơi Đa Dạng
ST666 cung cấp một danh mục trò chơi cá cược đa dạng, đáp ứng mọi nhu cầu và sở thích của người chơi. Từ thể thao, bắn cá, game bài, cho đến xổ số và live casino, tất cả đều được tối ưu hóa để mang lại cảm giác hứng thú cho người tham gia. Đặc biệt, với Live Casino, người chơi sẽ được trải nghiệm cá cược với các dealer thật thông qua hình thức phát trực tiếp, tạo cảm giác như đang tham gia tại các sòng bài thực tế.
Tỷ Lệ Cược Cạnh Tranh
Một trong những ưu điểm nổi bật của ST666 chính là tỷ lệ cược cực kỳ cạnh tranh, giúp người chơi tối ưu hóa lợi nhuận của mình. Các trận đấu thể thao được cập nhật liên tục với tỷ lệ cược hấp dẫn, tạo cơ hội chiến thắng lớn cho những ai yêu thích cá cược thể thao.
Bảo Mật An Toàn Tuyệt Đối
Yếu tố bảo mật luôn là một trong những tiêu chí hàng đầu khi chọn nhà cái cá cược. ST666 sử dụng công nghệ mã hóa hiện đại để bảo vệ thông tin cá nhân và các giao dịch tài chính của người chơi, đảm bảo mọi dữ liệu luôn được bảo mật tuyệt đối. Người chơi hoàn toàn có thể yên tâm khi tham gia cá cược tại đây.
Chăm Sóc Khách Hàng Chuyên Nghiệp
Dịch vụ chăm sóc khách hàng của ST666 luôn sẵn sàng hỗ trợ 24/7 qua nhiều kênh khác nhau như Live Chat, WhatsApp, Facebook, đảm bảo giải đáp mọi thắc mắc và xử lý các vấn đề nhanh chóng. Đội ngũ nhân viên tại đây được đào tạo chuyên nghiệp, tận tâm và chu đáo, luôn đặt lợi ích của khách hàng lên hàng đầu.
Ưu Đãi Hấp Dẫn
ST666 không chỉ nổi bật với các sản phẩm cá cược mà còn thu hút người chơi bởi các chương trình khuyến mãi hấp dẫn. Người chơi có thể nhận được nhiều ưu đãi như 280k miễn phí khi đăng nhập hàng ngày, cùng các chương trình thưởng nạp và hoàn tiền liên tục, giúp tối đa hóa cơ hội chiến thắng.
Lý Do ST666 Là Lựa Chọn Hàng Đầu
Sự kết hợp hoàn hảo giữa giao diện hiện đại, hệ thống trò chơi đa dạng, dịch vụ khách hàng tận tâm và tỷ lệ cược cạnh tranh đã giúp ST666 trở thành một trong những nhà cái cá cược trực tuyến uy tín hàng đầu tại Việt Nam. Đối với những ai đang tìm kiếm một nhà cái an toàn và chuyên nghiệp, ST666 chắc chắn sẽ là lựa chọn không thể bỏ qua.
Kết Luận
Với những ưu điểm vượt trội, ST666 xứng đáng là địa chỉ cá cược uy tín và an toàn cho tất cả người chơi. Đăng ký ngay hôm nay để trải nghiệm hệ thống cá cược đẳng cấp và nhận những ưu đãi hấp dẫn từ ST666!
Over 7 years in development, the Rollga Method™ combines trigger points, acupressure points, fascial lines, meridians, and techniques like ART (Active Release Technique), MAT (Muscle Activation Technique), RPR (Reflexive Performance Reset) and others to optimize one’s health thru a new system of self care.
Download the Rollga App to learn about & tap into all that Rollga has to offer!
Nhà cái ST666 được biết đến là sân chơi uy tín cung cấp các sản phẩm trò chơi cực kỳ đa dạng và chất lượng. Số lượng người tham gia vào hệ thống ngày càng tăng cao và chưa có dấu hiệu dừng lại. Hướng dẫn tham gia nhà cái nếu như anh em muốn tìm kiếm cơ hội nhận thưởng khủng. Hãy cùng khám phá những thông tin cần biết tại nhà cái để đặt cược và săn thưởng thành công.
Профессиональный сервисный центр где отремонтировать телефон сервис телефонов
Профессиональный сервисный центр по ремонту сотовых телефонов в Москве.
Мы предлагаем: ремонт смартфонов рядом
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Сервисный центр предлагает починка квадрокоптеров betafpv выездной ремонт квадрокоптеров betafpv
покупку франшизы https://franshizy12.ru .
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервисные центры в челябинске
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
быстрый вывод из запоя в стационаре быстрый вывод из запоя в стационаре .
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервис центры бытовой техники барнаул
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
https://унарзана.рф/
комета сайт kometa casino
Kometa Casino: Превосходный вариант для ценителей азартных игр
Если вы увлекаетесь ставками и выбираете платформу, что дает доступ к большой ассортимент слотов и игр с живыми дилерами, а к тому же большие бонусы, Казино Kometa — это то место, на котором вас ждут яркие эмоции. Попробуем рассмотрим, что выделяет Kometa Casino таким особенным и почему клиенты выбирают этом сайте для своих развлечений.
### Основные характеристики Kometa Casino
Казино Kometa — это всемирная игровая платформа, которая была запущена в 2024 году и сейчас уже получила внимание игроков по глобально. Вот основные черты, которые отличают данную платформу:
Черта Детали
Год создания 2024-й
Охват Международная
Число игр Свыше 1000
Регистрация Кюрасао
Мобильная Версия Присутствует
Методы платежей Visa, Mastercard, Skrill
Служба поддержки 24 часа в сутки
Приветственные бонусы Щедрые бонусы
Защита данных SSL Шифрование
### Почему выбирают Казино Kometa?
#### Программа лояльности
Одним из самых привлекательных фишек Kometa Casino становится уникальная программа лояльности. Чем больше вы играете, тем выше ваши бонусы. Программа включает семи уровней:
– **Уровень 1 — Земля**: Кэшбек 3% от затрат за 7 дней.
– **Уровень 2 — Луна**: Кэшбек 5% на ставки от 5 000 до 10 000 RUB.
– **Уровень 3 — Венера**: Возврат 7% при ставках на сумму от 10 001 до 50 000 рублей.
– **Марс (уровень 4)**: 8% бонуса при ставках от 50 001 до 150 000 ?.
– **Юпитер (уровень 5)**: Кэшбек 10% при ставках свыше 150 000 рублей.
– **Уровень 6 — Сатурн**: 11% кэшбек.
– **Уран (уровень 7)**: 12% кэшбек максимум 12%.
#### Постоянные бонусы
Для сохранения высокого уровня азарта, Kometa Casino предлагает бонусы каждую неделю, кэшбек и фриспины для новичков. Регулярные вознаграждения помогают сохранять интерес на каждой стадии игры.
#### Широкий выбор игр
Более 1000 игр, включая слоты, настольные развлечения и живое казино, создают Казино Kometa сайтом, где каждый найдет подходящее развлечение. Вы можете наслаждаться как классическими слотами, так и новейшими играми от ведущих провайдеров. Прямые дилеры создают играм ощущение реального казино, воссоздавая дух казино.
Начните массовую индексацию ссылок в Google прямо cейчас!
Быстрая индексация ссылок имеет ключевое значение для успеха вашего онлайн-бизнеса. Чем быстрее поисковые системы обнаружат и проиндексируют ваши ссылки, тем быстрее вы сможете привлечь новую аудиторию и повысить позиции вашего сайта в результатах поиска.
Не теряйте времени! Начните пользоваться нашим сервисом для ускоренной индексации внешних ссылок в Google и Yandex. Зарегистрируйтесь сегодня и получите первые результаты уже завтра. Ваш успех в ваших руках!
бесплатные фриспины за регистрацию без депозита
вывод из запоя в наркологическом стационаре http://www.vyvod-iz-zapoya-sochi15.ru/ .
Профессиональный сервисный центр по ремонту сотовых телефонов в Москве.
Мы предлагаем: ремонт телефонов москва дешево
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Over 7 years in development, the Rollga Method™ combines trigger points, acupressure points, fascial lines, meridians, and techniques like ART (Active Release Technique), MAT (Muscle Activation Technique), RPR (Reflexive Performance Reset) and others to optimize one’s health thru a new system of self care.
Download the Rollga App to learn about & tap into all that Rollga has to offer!
buy cozaar cheap – buy cozaar online cheap cheap cephalexin 500mg
https://otkazov-net.ru/
일본배대지
이용 안내 및 주요 정보
배송대행 이용방법
배송대행은 해외에서 구매한 상품을 중간지점(배대지)에 보내고, 이를 통해 한국으로 배송받는 서비스입니다. 먼저, 회원가입을 진행하고, 해당 배대지 주소를 이용해 상품을 주문한 후, 배송대행 신청서를 작성하여 배송 정보를 입력합니다. 모든 과정은 웹사이트를 통해 관리되며, 필요한 경우 고객센터를 통해 지원을 받을 수 있습니다.
구매대행 이용방법
구매대행은 해외 쇼핑몰에서 직접 구매가 어려운 경우, 대행 업체가 대신 구매해주는 서비스입니다. 고객이 원하는 상품 정보를 제공하면, 구매대행 신청서를 작성하고 대행료와 함께 결제하면 업체가 구매를 완료해줍니다. 이후 상품이 배대지로 도착하면 배송대행 절차를 통해 상품을 수령할 수 있습니다.
배송비용 안내
배송비용은 상품의 무게, 크기, 배송 지역에 따라 다르며, 계산기는 웹사이트에서 제공됩니다. 부피무게가 큰 제품이나 특수 제품은 추가 비용이 발생할 수 있습니다. 항공과 해운에 따른 요금 차이도 고려해야 합니다.
부가서비스
추가 포장 서비스, 검역 서비스, 폐기 서비스 등이 제공되며, 필요한 경우 신청서를 작성하여 서비스 이용이 가능합니다. 파손 위험이 있는 제품의 경우 포장 보완 서비스를 신청하는 것이 좋습니다.
관/부가세 안내
수입된 상품에 대한 관세와 부가세는 상품의 종류와 가격에 따라 부과됩니다. 이를 미리 확인하고, 추가 비용을 예상하여 계산하는 것이 중요합니다.
수입금지 품목
가스제품(히터), 폭발물, 위험물 등은 수입이 금지된 품목에 속합니다. 항공 및 해상 운송이 불가하니, 반드시 해당 품목을 확인 후 주문해야 합니다.
폐기/검역 안내
검역이 필요한 상품이나 폐기가 필요한 경우, 사전에 관련 부가서비스를 신청해야 합니다. 해당 사항에 대해 미리 안내받고 처리할 수 있도록 주의해야 합니다.
교환/반품 안내
교환 및 반품 절차는 상품을 배송받은 후 7일 이내에 신청이 가능합니다. 단, 일부 상품은 교환 및 반품이 제한될 수 있으니 사전에 정책을 확인하는 것이 좋습니다.
재고관리 시스템
재고관리는 배대지에서 보관 중인 상품의 상태를 실시간으로 확인할 수 있는 시스템입니다. 재고 신청을 통해 상품의 상태를 확인하고, 필요한 경우 배송 또는 폐기 요청을 할 수 있습니다.
노데이타 처리방법
노데이타 상태의 상품은 배송 추적이 어려운 경우 발생합니다. 이런 경우 고객센터를 통해 문의하고 문제를 해결해야 합니다.
소비세환급 및 Q&A
일본에서 상품을 구매할 때 적용된 소비세를 환급받을 수 있는 서비스입니다. 해당 신청서는 구체적인 절차에 따라 작성하고 제출해야 합니다. Q&A를 통해 자주 묻는 질문을 확인하고, 추가 문의 사항은 고객센터에 연락해 해결할 수 있습니다.
고객지원
고객센터는 1:1 문의, 카카오톡 상담 등을 통해 서비스 이용 중 발생하는 문제나 문의사항을 해결할 수 있도록 지원합니다.
서비스 관련 공지사항
파손이 쉬운 제품의 경우, 추가 포장 보완을 반드시 요청해야 합니다.
가스제품(히터)은 통관이 불가하므로 구매 전 확인 바랍니다.
항공 운송 비용이 대폭 인하되었습니다.
1win bet apk download https://www.1winapkdownload1win.com .
Профессиональный сервисный центр отремонтировать телефон починка телефонов
Профессиональный сервисный центр по ремонту сотовых телефонов в Москве.
Мы предлагаем: ремонт ноутбуков дешево
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
купить диплом нового образца в самаре orik-diploms.ru .
이용 안내 및 주요 정보
배송대행 이용방법
배송대행은 해외에서 구매한 상품을 중간지점(배대지)에 보내고, 이를 통해 한국으로 배송받는 서비스입니다. 먼저, 회원가입을 진행하고, 해당 배대지 주소를 이용해 상품을 주문한 후, 배송대행 신청서를 작성하여 배송 정보를 입력합니다. 모든 과정은 웹사이트를 통해 관리되며, 필요한 경우 고객센터를 통해 지원을 받을 수 있습니다.
구매대행 이용방법
구매대행은 해외 쇼핑몰에서 직접 구매가 어려운 경우, 대행 업체가 대신 구매해주는 서비스입니다. 고객이 원하는 상품 정보를 제공하면, 구매대행 신청서를 작성하고 대행료와 함께 결제하면 업체가 구매를 완료해줍니다. 이후 상품이 배대지로 도착하면 배송대행 절차를 통해 상품을 수령할 수 있습니다.
배송비용 안내
배송비용은 상품의 무게, 크기, 배송 지역에 따라 다르며, 계산기는 웹사이트에서 제공됩니다. 부피무게가 큰 제품이나 특수 제품은 추가 비용이 발생할 수 있습니다. 항공과 해운에 따른 요금 차이도 고려해야 합니다.
부가서비스
추가 포장 서비스, 검역 서비스, 폐기 서비스 등이 제공되며, 필요한 경우 신청서를 작성하여 서비스 이용이 가능합니다. 파손 위험이 있는 제품의 경우 포장 보완 서비스를 신청하는 것이 좋습니다.
관/부가세 안내
수입된 상품에 대한 관세와 부가세는 상품의 종류와 가격에 따라 부과됩니다. 이를 미리 확인하고, 추가 비용을 예상하여 계산하는 것이 중요합니다.
수입금지 품목
가스제품(히터), 폭발물, 위험물 등은 수입이 금지된 품목에 속합니다. 항공 및 해상 운송이 불가하니, 반드시 해당 품목을 확인 후 주문해야 합니다.
폐기/검역 안내
검역이 필요한 상품이나 폐기가 필요한 경우, 사전에 관련 부가서비스를 신청해야 합니다. 해당 사항에 대해 미리 안내받고 처리할 수 있도록 주의해야 합니다.
교환/반품 안내
교환 및 반품 절차는 상품을 배송받은 후 7일 이내에 신청이 가능합니다. 단, 일부 상품은 교환 및 반품이 제한될 수 있으니 사전에 정책을 확인하는 것이 좋습니다.
재고관리 시스템
재고관리는 배대지에서 보관 중인 상품의 상태를 실시간으로 확인할 수 있는 시스템입니다. 재고 신청을 통해 상품의 상태를 확인하고, 필요한 경우 배송 또는 폐기 요청을 할 수 있습니다.
노데이타 처리방법
노데이타 상태의 상품은 배송 추적이 어려운 경우 발생합니다. 이런 경우 고객센터를 통해 문의하고 문제를 해결해야 합니다.
소비세환급 및 Q&A
일본에서 상품을 구매할 때 적용된 소비세를 환급받을 수 있는 서비스입니다. 해당 신청서는 구체적인 절차에 따라 작성하고 제출해야 합니다. Q&A를 통해 자주 묻는 질문을 확인하고, 추가 문의 사항은 고객센터에 연락해 해결할 수 있습니다.
고객지원
고객센터는 1:1 문의, 카카오톡 상담 등을 통해 서비스 이용 중 발생하는 문제나 문의사항을 해결할 수 있도록 지원합니다.
서비스 관련 공지사항
파손이 쉬운 제품의 경우, 추가 포장 보완을 반드시 요청해야 합니다.
가스제품(히터)은 통관이 불가하므로 구매 전 확인 바랍니다.
항공 운송 비용이 대폭 인하되었습니다.
일본배대지
이용 안내 및 주요 정보
배송대행 이용방법
배송대행은 해외에서 구매한 상품을 중간지점(배대지)에 보내고, 이를 통해 한국으로 배송받는 서비스입니다. 먼저, 회원가입을 진행하고, 해당 배대지 주소를 이용해 상품을 주문한 후, 배송대행 신청서를 작성하여 배송 정보를 입력합니다. 모든 과정은 웹사이트를 통해 관리되며, 필요한 경우 고객센터를 통해 지원을 받을 수 있습니다.
구매대행 이용방법
구매대행은 해외 쇼핑몰에서 직접 구매가 어려운 경우, 대행 업체가 대신 구매해주는 서비스입니다. 고객이 원하는 상품 정보를 제공하면, 구매대행 신청서를 작성하고 대행료와 함께 결제하면 업체가 구매를 완료해줍니다. 이후 상품이 배대지로 도착하면 배송대행 절차를 통해 상품을 수령할 수 있습니다.
배송비용 안내
배송비용은 상품의 무게, 크기, 배송 지역에 따라 다르며, 계산기는 웹사이트에서 제공됩니다. 부피무게가 큰 제품이나 특수 제품은 추가 비용이 발생할 수 있습니다. 항공과 해운에 따른 요금 차이도 고려해야 합니다.
부가서비스
추가 포장 서비스, 검역 서비스, 폐기 서비스 등이 제공되며, 필요한 경우 신청서를 작성하여 서비스 이용이 가능합니다. 파손 위험이 있는 제품의 경우 포장 보완 서비스를 신청하는 것이 좋습니다.
관/부가세 안내
수입된 상품에 대한 관세와 부가세는 상품의 종류와 가격에 따라 부과됩니다. 이를 미리 확인하고, 추가 비용을 예상하여 계산하는 것이 중요합니다.
수입금지 품목
가스제품(히터), 폭발물, 위험물 등은 수입이 금지된 품목에 속합니다. 항공 및 해상 운송이 불가하니, 반드시 해당 품목을 확인 후 주문해야 합니다.
폐기/검역 안내
검역이 필요한 상품이나 폐기가 필요한 경우, 사전에 관련 부가서비스를 신청해야 합니다. 해당 사항에 대해 미리 안내받고 처리할 수 있도록 주의해야 합니다.
교환/반품 안내
교환 및 반품 절차는 상품을 배송받은 후 7일 이내에 신청이 가능합니다. 단, 일부 상품은 교환 및 반품이 제한될 수 있으니 사전에 정책을 확인하는 것이 좋습니다.
재고관리 시스템
재고관리는 배대지에서 보관 중인 상품의 상태를 실시간으로 확인할 수 있는 시스템입니다. 재고 신청을 통해 상품의 상태를 확인하고, 필요한 경우 배송 또는 폐기 요청을 할 수 있습니다.
노데이타 처리방법
노데이타 상태의 상품은 배송 추적이 어려운 경우 발생합니다. 이런 경우 고객센터를 통해 문의하고 문제를 해결해야 합니다.
소비세환급 및 Q&A
일본에서 상품을 구매할 때 적용된 소비세를 환급받을 수 있는 서비스입니다. 해당 신청서는 구체적인 절차에 따라 작성하고 제출해야 합니다. Q&A를 통해 자주 묻는 질문을 확인하고, 추가 문의 사항은 고객센터에 연락해 해결할 수 있습니다.
고객지원
고객센터는 1:1 문의, 카카오톡 상담 등을 통해 서비스 이용 중 발생하는 문제나 문의사항을 해결할 수 있도록 지원합니다.
서비스 관련 공지사항
파손이 쉬운 제품의 경우, 추가 포장 보완을 반드시 요청해야 합니다.
가스제품(히터)은 통관이 불가하므로 구매 전 확인 바랍니다.
항공 운송 비용이 대폭 인하되었습니다.
instagram online stories viewer https://anstoriesviewer.com .
вывод из запоя стационар вывод из запоя стационар .
insta viewer insta viewer .
скачать комета kometa casino
Kometa Casino: Лучший выбор для фанатов игр на удачу
В случае если вы интересуетесь азартными играми и рассматриваете площадку, которая предлагает широкий ассортимент игровых автоматов и игр с живыми дилерами, а плюс большие бонусы, Казино Kometa — это то место, где вы найдете незабываемый опыт. Попробуем рассмотрим, какие факторы превращает данное казино уникальным и по каким причинам посетители выбирают его для игры.
### Ключевые черты Казино Kometa
Казино Kometa — это глобальная игровая платформа, которая была основана в 2024-м и уже сейчас привлекла интерес клиентов по всему миру. Вот основные черты, которые сравнивают с другими этот сайт:
Функция Описание
Год Основания 2024-й
География Доступа Всемирная
Число игр Больше тысячи
Регистрация Кюрасао
Поддержка мобильных Доступна
Способы Оплаты Популярные платежные системы
Техподдержка 24/7 Чат и Email
Приветственные бонусы Акции и бонусы
Безопасность Шифрование SSL
### Что привлекает в Казино Kometa?
#### Программа лояльности
Одним из интересных особенностей Kometa Casino является система бонусов. Чем больше вы играете, тем больше ваши вознаграждения. Система состоит из многоуровневую систему:
– **Уровень 1 — Земля**: Кэшбек 3% 3% от затрат за 7 дней.
– **Луна (уровень 2)**: Возврат 5% при ставках от 5 000 до 10 000 рублей.
– **Венера (уровень 3)**: 7% возврата при ставках на сумму от 10 001 до 50 000 ?.
– **Уровень 4 — Марс**: 8% кэшбек при ставках от 50 001 до 150 000 ?.
– **Юпитер (уровень 5)**: 10% возврата при общей ставке свыше 150 000 рублей.
– **Сатурн (уровень 6)**: Возврат 11%.
– **Уровень 7 — Уран**: Максимальный возврат максимум 12%.
#### Акции и возврат средств
С целью удержания высокого уровня азарта, Kometa Casino предоставляет еженедельные бонусы, возврат средств и фриспины для всех новых игроков. Регулярные вознаграждения помогают поддерживать азарт на в процессе игры.
#### Большое количество развлечений
Огромное количество развлечений, включая автоматы, настольные игры и лайв-игры, превращают Kometa Casino местом, где вы найдете игру по душе. Каждый может играть стандартными автоматами, а также новинками от известных разработчиков. Живые дилеры придают атмосфере настоящее казино, формируя атмосферу азартного дома.
Сервисный центр предлагает ремонт toshiba satellite l650 цены ремонт toshiba satellite l650
purchase cleocin pill – indomethacin over the counter purchase indomethacin generic
Как получить диплом о среднем образовании в Москве и других городах
ironway.ru/forum/viewtopic.php?f=5&t=47746
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервис центры бытовой техники москва
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Пошаговая инструкция по официальной покупке диплома о высшем образовании
Профессиональный сервисный центр по ремонту духовых шкафов в Москве.
Мы предлагаем: ремонт духовых шкафов в москве на дому
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Cách Tối Đa Hóa Tiền Thưởng Tại RGBET
META title: Cách tối ưu hóa tiền thưởng trên RGBET
META description: Học cách tối đa hóa tiền thưởng của bạn trên RGBET bằng các mẹo và chiến lược cá cược hiệu quả nhất.
Giới thiệu
Tiền thưởng là cơ hội tuyệt vời để tăng cơ hội thắng lớn mà không phải bỏ ra nhiều vốn. RGBET cung cấp rất nhiều loại khuyến mãi hấp dẫn, hãy cùng khám phá cách tối ưu hóa chúng!
1. Đọc kỹ điều kiện khuyến mãi
Mỗi chương trình thưởng đều có điều kiện riêng, bạn cần đọc kỹ để đảm bảo không bỏ lỡ cơ hội.
2. Đặt cược theo mức yêu cầu
Để nhận thưởng, hãy đảm bảo rằng số tiền cược của bạn đạt yêu cầu tối thiểu.
3. Tận dụng tiền thưởng nạp đầu tiên
Đây là cơ hội để bạn có thêm vốn ngay từ đầu. Hãy lựa chọn mức nạp phù hợp với ngân sách.
4. Theo dõi khuyến mãi hàng tuần
RGBET liên tục đưa ra các chương trình khuyến mãi hàng tuần. Đừng bỏ lỡ cơ hội nhận thêm tiền thưởng!
5. Sử dụng điểm VIP
Khi bạn đạt mức VIP, điểm thưởng có thể được chuyển thành tiền mặt, giúp bạn tối ưu hóa lợi nhuận.
Kết luận
Biết cách tận dụng tiền thưởng không chỉ giúp bạn có thêm tiền cược mà còn tăng cơ hội thắng lớn.
купить диплом морские landik-diploms.ru .
rgbet
Cách Tối Đa Hóa Tiền Thưởng Tại RGBET
META title: Cách tối ưu hóa tiền thưởng trên RGBET
META description: Học cách tối đa hóa tiền thưởng của bạn trên RGBET bằng các mẹo và chiến lược cá cược hiệu quả nhất.
Giới thiệu
Tiền thưởng là cơ hội tuyệt vời để tăng cơ hội thắng lớn mà không phải bỏ ra nhiều vốn. RGBET cung cấp rất nhiều loại khuyến mãi hấp dẫn, hãy cùng khám phá cách tối ưu hóa chúng!
1. Đọc kỹ điều kiện khuyến mãi
Mỗi chương trình thưởng đều có điều kiện riêng, bạn cần đọc kỹ để đảm bảo không bỏ lỡ cơ hội.
2. Đặt cược theo mức yêu cầu
Để nhận thưởng, hãy đảm bảo rằng số tiền cược của bạn đạt yêu cầu tối thiểu.
3. Tận dụng tiền thưởng nạp đầu tiên
Đây là cơ hội để bạn có thêm vốn ngay từ đầu. Hãy lựa chọn mức nạp phù hợp với ngân sách.
4. Theo dõi khuyến mãi hàng tuần
RGBET liên tục đưa ra các chương trình khuyến mãi hàng tuần. Đừng bỏ lỡ cơ hội nhận thêm tiền thưởng!
5. Sử dụng điểm VIP
Khi bạn đạt mức VIP, điểm thưởng có thể được chuyển thành tiền mặt, giúp bạn tối ưu hóa lợi nhuận.
Kết luận
Biết cách tận dụng tiền thưởng không chỉ giúp bạn có thêm tiền cược mà còn tăng cơ hội thắng lớn.
Tại Sao Nên Chọn RGBET Là Nền Tảng Cá Cược Trực Tuyến Hàng Đầu
META title: Vì sao RGBET là nền tảng cá cược tốt nhất cho người chơi Việt Nam
META description: Tìm hiểu những lý do RGBET là lựa chọn hàng đầu cho người chơi Việt Nam với giao diện hiện đại, khuyến mãi hấp dẫn và nạp rút nhanh chóng.
Giới thiệu
RGBET không chỉ là một trang cá cược trực tuyến thông thường. Với những tính năng nổi bật và các chương trình khuyến mãi hấp dẫn, đây là một trong những nền tảng được người chơi Việt Nam tin tưởng nhất.
1. Giao diện thân thiện
Giao diện của RGBET dễ sử dụng, thích hợp cho cả người mới và người chơi lâu năm.
2. Khuyến mãi hấp dẫn
Nền tảng này cung cấp nhiều chương trình khuyến mãi như thưởng nạp đầu, cashback, và chương trình VIP.
3. Nạp và rút tiền nhanh chóng
RGBET hỗ trợ nhiều phương thức thanh toán an toàn và nhanh chóng, từ ngân hàng nội địa đến ví điện tử.
4. Hỗ trợ khách hàng 24/7
RGBET có đội ngũ hỗ trợ luôn sẵn sàng giải đáp mọi thắc mắc của người chơi mọi lúc.
Kết luận
RGBET không chỉ đem lại trải nghiệm cá cược tuyệt vời mà còn đảm bảo sự tiện lợi và uy tín cho người chơi.
Сервисный центр предлагает качественый ремонт парогенераторов beko мастерские ремонта парогенераторов beko
download 1win apk http://www.1wincotedivoireapk.com .
Официальная покупка школьного аттестата с упрощенным обучением в Москве
instagram profile [url=http://www.anonimviewer.com]instagram profile[/url] .
1win apk ios telecharger1winci.com .
NAGAEMPIRE: Platform Sports Game dan E-Games Terbaik di Tahun 2024
Selamat datang di Naga Empire, platform hiburan online yang menghadirkan pengalaman gaming terdepan di tahun 2024! Kami bangga menawarkan sports game, permainan kartu, dan berbagai fitur unggulan yang dirancang untuk memberikan Anda kesenangan dan keuntungan maksimal.
Keunggulan Pendaftaran dengan E-Wallet dan QRIS
Kami memprioritaskan kemudahan dan kecepatan dalam pengalaman bermain Anda:
Pendaftaran dengan E-Wallet: Daftarkan akun Anda dengan mudah menggunakan e-wallet favorit. Proses pendaftaran sangat cepat, memungkinkan Anda langsung memulai petualangan gaming tanpa hambatan.
QRIS Auto Proses dalam 1 Detik: Transaksi Anda diproses instan hanya dalam 1 detik dengan teknologi QRIS, memastikan pembayaran dan deposit berjalan lancar tanpa gangguan.
Sports Game dan Permainan Kartu Terbaik di Tahun 2024
Naga Empire menawarkan berbagai pilihan game menarik:
Sports Game Terlengkap: Dari taruhan olahraga hingga fantasy sports, kami menyediakan sensasi taruhan olahraga dengan kualitas terbaik.
Kartu Terbaik di 2024: Nikmati permainan kartu klasik hingga variasi modern dengan grafis yang menakjubkan, memberikan pengalaman bermain yang tak terlupakan.
Permainan Terlengkap dan Toto Terlengkap
Kami memiliki koleksi permainan yang sangat beragam:
Permainan Terlengkap: Temukan berbagai pilihan permainan seperti slot mesin, kasino, hingga permainan berbasis keterampilan, semua tersedia di Naga Empire.
Toto Terlengkap: Layanan Toto Online kami menawarkan pilihan taruhan yang lengkap dengan odds yang kompetitif, memberikan pengalaman taruhan yang optimal.
Bonus Melimpah dan Turnover Terendah
Bonus Melimpah: Dapatkan bonus mulai dari bonus selamat datang, bonus setoran, hingga promosi eksklusif. Kami selalu memberikan nilai lebih pada setiap taruhan Anda.
Turnover Terendah: Dengan turnover rendah, Anda dapat meraih kemenangan lebih mudah dan meningkatkan keuntungan dari setiap permainan.
Naga Empire adalah tempat yang tepat bagi Anda yang mencari pengalaman gaming terbaik di tahun 2024. Bergabunglah sekarang dan rasakan sensasi kemenangan di platform yang paling komprehensif!
вывод из запоя цена ростов вывод из запоя цена ростов .
Быстрая покупка диплома старого образца: возможные риски
silich.ru/forum/member.php?u=4810
Полезный сервис быстрого загона ссылок сайта в индексация поисковой системы – индексация в гугл
топ франшиз топ франшиз .
Полезные советы по безопасной покупке диплома о высшем образовании
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
voprosnek.flybb.ru/viewtopic.php?f=2&t=293
актуальное зеркало kometa casino
Казино Kometa: Превосходный выбор для ценителей игр на удачу
Когда вы интересуетесь ставками и ищете площадку, что дает доступ к огромный выбор игровых автоматов и лайв-игр, а плюс выгодные предложения, Kometa Casino — это тот сайт, где вы найдете незабываемые впечатления. Попробуем узнаем, какие факторы делает данное казино таким особенным и почему посетители выбирают этой платформе для своих развлечений.
### Ключевые черты Казино Kometa
Kometa Casino — это глобальная казино, которая была основана в 2024-м и уже сейчас завоевала признание клиентов по всему миру. Вот основные моменты, которые отличают Kometa Casino:
Функция Детали
Год Основания 2024-й
География Доступа Всемирная
Объем игр Более 1000
Сертификация Кюрасао
Поддержка мобильных Присутствует
Методы платежей Visa, Mastercard, Skrill
Техподдержка Круглосуточная поддержка
Бонусы и Акции Приветственные бонусы и Еженедельные выигрыши
Защита данных SSL защита
### Зачем играют в Kometa Casino?
#### Система поощрений
Одной из интересных функций Kometa Casino считается поощрительная программа. Чем больше ставок, тем больше ваши вознаграждения. Программа включает многоуровневую систему:
– **Уровень 1 — Земля**: Кэшбек 3% 3% от потраченных средств за 7 дней.
– **Уровень 2 — Луна**: 5% кэшбек на ставки от 5 000 до 10 000 ?.
– **Венера (уровень 3)**: Кэшбек 7% при игре от 10 001 до 50 000 ?.
– **Марс (уровень 4)**: 8% кэшбек при ставках от 50 001 до 150 000 рублей.
– **Уровень 5 — Юпитер**: 10% возврата при общей ставке свыше 150 000 RUB.
– **Уровень 6 — Сатурн**: Возврат 11%.
– **Уран (уровень 7)**: Максимальный возврат до 12%.
#### Акции и возврат средств
Для сохранения высокого уровня азарта, Kometa Casino проводит бонусы каждую неделю, возврат средств и фриспины для всех новых игроков. Постоянные подарки способствуют поддерживать азарт на протяжении всей игры.
#### Большое количество развлечений
Свыше тысячи игр, включая автоматы, настольные развлечения и лайв-игры, превращают Kometa Casino площадкой, где любой найдет развлечение на вкус. Вы можете наслаждаться как классическими слотами, и современными слотами от ведущих провайдеров. Дилеры в реальном времени придают играм еще больше реализма, формируя атмосферу азартного дома.
ответственность за купленный диплом arusak-diploms.ru .
Сколько стоит диплом высшего и среднего образования и как его получить?
เกมสล็อตออนไลน์
สล็อต888 เป็นหนึ่งในแพลตฟอร์มเกมสล็อตออนไลน์ที่ได้รับความนิยมสูงสุดในปัจจุบัน โดยมีความโดดเด่นด้วยการให้บริการเกมสล็อตที่หลากหลายและมีคุณภาพ รวมถึงฟีเจอร์ที่ช่วยให้ผู้เล่นสามารถเพลิดเพลินกับการเล่นได้อย่างเต็มที่ ในบทความนี้ เราจะมาพูดถึงฟีเจอร์และจุดเด่นของสล็อต888 ที่ทำให้เว็บไซต์นี้ได้รับความนิยมเป็นอย่างมาก
ฟีเจอร์เด่นของ PG สล็อต888
ระบบฝากถอนเงินอัตโนมัติที่รวดเร็ว สล็อต888 ให้บริการระบบฝากถอนเงินแบบอัตโนมัติที่สามารถทำรายการได้ทันที ไม่ต้องรอนาน ไม่ว่าจะเป็นการฝากหรือถอนก็สามารถทำได้ภายในไม่กี่วินาที รองรับการใช้งานผ่านทรูวอลเล็ทและช่องทางอื่น ๆ โดยไม่มีขั้นต่ำในการฝากถอน
รองรับทุกอุปกรณ์ ทุกแพลตฟอร์ม ไม่ว่าคุณจะเล่นจากอุปกรณ์ใดก็ตาม สล็อต888 รองรับทั้งคอมพิวเตอร์ แท็บเล็ต และสมาร์ทโฟน ไม่ว่าจะเป็นระบบ iOS หรือ Android คุณสามารถเข้าถึงเกมสล็อตได้ทุกที่ทุกเวลาเพียงแค่มีอินเทอร์เน็ต
โปรโมชั่นและโบนัสมากมาย สำหรับผู้เล่นใหม่และลูกค้าประจำ สล็อต888 มีโปรโมชั่นต้อนรับ รวมถึงโบนัสพิเศษ เช่น ฟรีสปินและโบนัสเครดิตเพิ่ม ทำให้การเล่นเกมสล็อตกับเราเป็นเรื่องสนุกและมีโอกาสทำกำไรมากยิ่งขึ้น
ความปลอดภัยสูงสุด เรื่องความปลอดภัยเป็นสิ่งที่สล็อต888 ให้ความสำคัญเป็นอย่างยิ่ง เราใช้เทคโนโลยีการเข้ารหัสข้อมูลขั้นสูงเพื่อปกป้องข้อมูลส่วนบุคคลของลูกค้า ระบบฝากถอนเงินยังมีมาตรการรักษาความปลอดภัยที่เข้มงวด ทำให้ลูกค้ามั่นใจในการใช้บริการกับเรา
ทดลองเล่นสล็อตฟรี
สล็อต888 ยังมีบริการให้ผู้เล่นสามารถทดลองเล่นสล็อตได้ฟรี ซึ่งเป็นโอกาสที่ดีในการทดลองเล่นเกมต่าง ๆ ที่มีอยู่บนเว็บไซต์ เช่น Phoenix Rises, Dream Of Macau, Ways Of Qilin, Caishens Wins และเกมยอดนิยมอื่น ๆ ที่มีกราฟิกสวยงามและรูปแบบการเล่นที่น่าสนใจ
ไม่ว่าจะเป็นเกมแนวผจญภัย เช่น Rise Of Apollo, Dragon Hatch หรือเกมที่มีธีมแห่งความมั่งคั่งอย่าง Crypto Gold, Fortune Tiger, Lucky Piggy ทุกเกมได้รับการออกแบบมาเพื่อสร้างประสบการณ์การเล่นที่น่าจดจำและเต็มไปด้วยความสนุกสนาน
บทสรุป
สล็อต888 เป็นแพลตฟอร์มที่ครบเครื่องเรื่องเกมสล็อตออนไลน์ ด้วยฟีเจอร์ที่ทันสมัย โปรโมชั่นที่น่าสนใจ และระบบรักษาความปลอดภัยที่เข้มงวด ทำให้คุณมั่นใจได้ว่าการเล่นกับสล็อต888 จะเป็นประสบการณ์ที่ปลอดภัยและเต็มไปด้วยความสนุก
Как оказалось, купить диплом кандидата наук не так уж и сложно
hustlacrips.forumex.ru/viewtopic.php?f=9&t=262
купить диплом о высшем образовании в россии [url=https://russa-diploms.ru/]russa-diploms.ru[/url] .
Где и как купить диплом о высшем образовании без лишних рисков
нью ретро казино [url=www.newretrocasino-casino2.ru]нью ретро казино[/url] .
1win apk ios xn--tlcharger1win-bhbb.com .
автоматические карнизы для штор заказать elektrokarniz-dlya-shtor11.ru .
เกมสล็อตออนไลน์
สล็อต888 เป็นหนึ่งในแพลตฟอร์มเกมสล็อตออนไลน์ที่ได้รับความนิยมสูงสุดในปัจจุบัน โดยมีความโดดเด่นด้วยการให้บริการเกมสล็อตที่หลากหลายและมีคุณภาพ รวมถึงฟีเจอร์ที่ช่วยให้ผู้เล่นสามารถเพลิดเพลินกับการเล่นได้อย่างเต็มที่ ในบทความนี้ เราจะมาพูดถึงฟีเจอร์และจุดเด่นของสล็อต888 ที่ทำให้เว็บไซต์นี้ได้รับความนิยมเป็นอย่างมาก
ฟีเจอร์เด่นของ PG สล็อต888
ระบบฝากถอนเงินอัตโนมัติที่รวดเร็ว สล็อต888 ให้บริการระบบฝากถอนเงินแบบอัตโนมัติที่สามารถทำรายการได้ทันที ไม่ต้องรอนาน ไม่ว่าจะเป็นการฝากหรือถอนก็สามารถทำได้ภายในไม่กี่วินาที รองรับการใช้งานผ่านทรูวอลเล็ทและช่องทางอื่น ๆ โดยไม่มีขั้นต่ำในการฝากถอน
รองรับทุกอุปกรณ์ ทุกแพลตฟอร์ม ไม่ว่าคุณจะเล่นจากอุปกรณ์ใดก็ตาม สล็อต888 รองรับทั้งคอมพิวเตอร์ แท็บเล็ต และสมาร์ทโฟน ไม่ว่าจะเป็นระบบ iOS หรือ Android คุณสามารถเข้าถึงเกมสล็อตได้ทุกที่ทุกเวลาเพียงแค่มีอินเทอร์เน็ต
โปรโมชั่นและโบนัสมากมาย สำหรับผู้เล่นใหม่และลูกค้าประจำ สล็อต888 มีโปรโมชั่นต้อนรับ รวมถึงโบนัสพิเศษ เช่น ฟรีสปินและโบนัสเครดิตเพิ่ม ทำให้การเล่นเกมสล็อตกับเราเป็นเรื่องสนุกและมีโอกาสทำกำไรมากยิ่งขึ้น
ความปลอดภัยสูงสุด เรื่องความปลอดภัยเป็นสิ่งที่สล็อต888 ให้ความสำคัญเป็นอย่างยิ่ง เราใช้เทคโนโลยีการเข้ารหัสข้อมูลขั้นสูงเพื่อปกป้องข้อมูลส่วนบุคคลของลูกค้า ระบบฝากถอนเงินยังมีมาตรการรักษาความปลอดภัยที่เข้มงวด ทำให้ลูกค้ามั่นใจในการใช้บริการกับเรา
ทดลองเล่นสล็อตฟรี
สล็อต888 ยังมีบริการให้ผู้เล่นสามารถทดลองเล่นสล็อตได้ฟรี ซึ่งเป็นโอกาสที่ดีในการทดลองเล่นเกมต่าง ๆ ที่มีอยู่บนเว็บไซต์ เช่น Phoenix Rises, Dream Of Macau, Ways Of Qilin, Caishens Wins และเกมยอดนิยมอื่น ๆ ที่มีกราฟิกสวยงามและรูปแบบการเล่นที่น่าสนใจ
ไม่ว่าจะเป็นเกมแนวผจญภัย เช่น Rise Of Apollo, Dragon Hatch หรือเกมที่มีธีมแห่งความมั่งคั่งอย่าง Crypto Gold, Fortune Tiger, Lucky Piggy ทุกเกมได้รับการออกแบบมาเพื่อสร้างประสบการณ์การเล่นที่น่าจดจำและเต็มไปด้วยความสนุกสนาน
บทสรุป
สล็อต888 เป็นแพลตฟอร์มที่ครบเครื่องเรื่องเกมสล็อตออนไลน์ ด้วยฟีเจอร์ที่ทันสมัย โปรโมชั่นที่น่าสนใจ และระบบรักษาความปลอดภัยที่เข้มงวด ทำให้คุณมั่นใจได้ว่าการเล่นกับสล็อต888 จะเป็นประสบการณ์ที่ปลอดภัยและเต็มไปด้วยความสนุก
Профессиональный сервисный центр по ремонту сотовых телефонов в Москве.
Мы предлагаем: ремонт ноутбука адреса и цены
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
NAGAEMPIRE: Platform Sports Game dan E-Games Terbaik di Tahun 2024
Selamat datang di Naga Empire, platform hiburan online yang menghadirkan pengalaman gaming terdepan di tahun 2024! Kami bangga menawarkan sports game, permainan kartu, dan berbagai fitur unggulan yang dirancang untuk memberikan Anda kesenangan dan keuntungan maksimal.
Keunggulan Pendaftaran dengan E-Wallet dan QRIS
Kami memprioritaskan kemudahan dan kecepatan dalam pengalaman bermain Anda:
Pendaftaran dengan E-Wallet: Daftarkan akun Anda dengan mudah menggunakan e-wallet favorit. Proses pendaftaran sangat cepat, memungkinkan Anda langsung memulai petualangan gaming tanpa hambatan.
QRIS Auto Proses dalam 1 Detik: Transaksi Anda diproses instan hanya dalam 1 detik dengan teknologi QRIS, memastikan pembayaran dan deposit berjalan lancar tanpa gangguan.
Sports Game dan Permainan Kartu Terbaik di Tahun 2024
Naga Empire menawarkan berbagai pilihan game menarik:
Sports Game Terlengkap: Dari taruhan olahraga hingga fantasy sports, kami menyediakan sensasi taruhan olahraga dengan kualitas terbaik.
Kartu Terbaik di 2024: Nikmati permainan kartu klasik hingga variasi modern dengan grafis yang menakjubkan, memberikan pengalaman bermain yang tak terlupakan.
Permainan Terlengkap dan Toto Terlengkap
Kami memiliki koleksi permainan yang sangat beragam:
Permainan Terlengkap: Temukan berbagai pilihan permainan seperti slot mesin, kasino, hingga permainan berbasis keterampilan, semua tersedia di Naga Empire.
Toto Terlengkap: Layanan Toto Online kami menawarkan pilihan taruhan yang lengkap dengan odds yang kompetitif, memberikan pengalaman taruhan yang optimal.
Bonus Melimpah dan Turnover Terendah
Bonus Melimpah: Dapatkan bonus mulai dari bonus selamat datang, bonus setoran, hingga promosi eksklusif. Kami selalu memberikan nilai lebih pada setiap taruhan Anda.
Turnover Terendah: Dengan turnover rendah, Anda dapat meraih kemenangan lebih mudah dan meningkatkan keuntungan dari setiap permainan.
Naga Empire adalah tempat yang tepat bagi Anda yang mencari pengalaman gaming terbaik di tahun 2024. Bergabunglah sekarang dan rasakan sensasi kemenangan di platform yang paling komprehensif!
купить диплом морские landik-diploms.ru .
st666
ST666 – Nhà Cái Uy Tín Với Nhiều Khuyến Mãi Hấp Dẫn
ST666 là một trong những sòng bài trực tuyến uy tín nhất, mang đến cho các thành viên nhiều chương trình khuyến mãi đa dạng và hấp dẫn. Chúng tôi luôn hy vọng rằng những ưu đãi đặc biệt này sẽ mang lại trải nghiệm cá cược tuyệt vời cho tất cả thành viên của mình.
Khuyến Mãi Nạp Đầu Thưởng 100%
NO.1: Thưởng 100% lần nạp đầu tiên Thông thường, các khuyến mãi nạp tiền lần đầu đi kèm với yêu cầu vòng cược rất cao, thường từ 20 vòng trở lên. Tuy nhiên, ST666 hiểu rằng người chơi thường đắn đo khi quyết định nạp tiền vào sòng bài trực tuyến. Do đó, chúng tôi chỉ yêu cầu 8 vòng cược, cho phép người chơi rút tiền một cách nhanh chóng trong vòng 5 phút.
Thưởng 100% khi Đăng Nhập ST666
NO.2: Thưởng 16% mỗi ngày ST666 mang đến cho bạn một ưu đãi không thể bỏ lỡ. Mỗi khi bạn nạp tiền vào tài khoản hàng ngày, bạn sẽ được nhận thêm 16% số tiền nạp. Đây là cơ hội tuyệt vời dành cho những ai yêu thích cá cược trực tuyến và muốn gia tăng cơ hội chiến thắng của mình.
Bảo Hiểm Hoàn 10% Mỗi Ngày
NO.3: Bảo hiểm hoàn tiền 10% ST666 không chỉ hỗ trợ người chơi trong những lần may mắn mà còn luôn đồng hành khi bạn không gặp may. Chương trình khuyến mãi “bảo hiểm hoàn tiền 10% tổng tiền nạp mỗi ngày” là cách chúng tôi khích lệ và động viên tinh thần game thủ, giúp bạn tiếp tục hành trình chinh phục các thử thách cá cược.
Giới Thiệu Bạn Bè Thưởng 999K
NO.4: Giới thiệu bạn bè – Thưởng 999K Chương trình “Giới thiệu bạn bè” của ST666 giúp bạn có cơ hội cá cược cùng bạn bè và người thân. Không những vậy, bạn còn có thể nhận được phần thưởng lên đến 999K khi giới thiệu người bạn của mình tham gia ST666. Đây chính là một ưu đãi tuyệt vời giúp bạn vừa có thêm người đồng hành, vừa nhận được thưởng hấp dẫn.
Đăng Nhập Nhận Ngay 280K
NO.5: Điểm danh nhận thưởng 280K Nếu bạn là thành viên thường xuyên của ST666, hãy đừng quên nhấp vào hộp quà hàng ngày để điểm danh. Chỉ cần đăng nhập liên tục trong 7 ngày, cơ hội nhận thưởng 280K sẽ thuộc về bạn!
Kết Luận
ST666 luôn nỗ lực không ngừng để mang lại những chương trình khuyến mãi hấp dẫn và thiết thực nhất cho người chơi. Dù bạn là người mới hay đã gắn bó lâu năm với nền tảng, ST666 cam kết cung cấp trải nghiệm cá cược tốt nhất, an toàn và công bằng. Hãy tham gia ngay để không bỏ lỡ các cơ hội tuyệt vời từ ST666!
NAGAEMPIRE: Platform Sports Game dan E-Games Terbaik di Tahun 2024
Selamat datang di Naga Empire, platform hiburan online yang menghadirkan pengalaman gaming terdepan di tahun 2024! Kami bangga menawarkan sports game, permainan kartu, dan berbagai fitur unggulan yang dirancang untuk memberikan Anda kesenangan dan keuntungan maksimal.
Keunggulan Pendaftaran dengan E-Wallet dan QRIS
Kami memprioritaskan kemudahan dan kecepatan dalam pengalaman bermain Anda:
Pendaftaran dengan E-Wallet: Daftarkan akun Anda dengan mudah menggunakan e-wallet favorit. Proses pendaftaran sangat cepat, memungkinkan Anda langsung memulai petualangan gaming tanpa hambatan.
QRIS Auto Proses dalam 1 Detik: Transaksi Anda diproses instan hanya dalam 1 detik dengan teknologi QRIS, memastikan pembayaran dan deposit berjalan lancar tanpa gangguan.
Sports Game dan Permainan Kartu Terbaik di Tahun 2024
Naga Empire menawarkan berbagai pilihan game menarik:
Sports Game Terlengkap: Dari taruhan olahraga hingga fantasy sports, kami menyediakan sensasi taruhan olahraga dengan kualitas terbaik.
Kartu Terbaik di 2024: Nikmati permainan kartu klasik hingga variasi modern dengan grafis yang menakjubkan, memberikan pengalaman bermain yang tak terlupakan.
Permainan Terlengkap dan Toto Terlengkap
Kami memiliki koleksi permainan yang sangat beragam:
Permainan Terlengkap: Temukan berbagai pilihan permainan seperti slot mesin, kasino, hingga permainan berbasis keterampilan, semua tersedia di Naga Empire.
Toto Terlengkap: Layanan Toto Online kami menawarkan pilihan taruhan yang lengkap dengan odds yang kompetitif, memberikan pengalaman taruhan yang optimal.
Bonus Melimpah dan Turnover Terendah
Bonus Melimpah: Dapatkan bonus mulai dari bonus selamat datang, bonus setoran, hingga promosi eksklusif. Kami selalu memberikan nilai lebih pada setiap taruhan Anda.
Turnover Terendah: Dengan turnover rendah, Anda dapat meraih kemenangan lebih mudah dan meningkatkan keuntungan dari setiap permainan.
Naga Empire adalah tempat yang tepat bagi Anda yang mencari pengalaman gaming terbaik di tahun 2024. Bergabunglah sekarang dan rasakan sensasi kemenangan di platform yang paling komprehensif!
rgbet77
Bạn đang tìm kiếm những trò chơi hot nhất và thú vị nhất tại sòng bạc trực tuyến? RGBET tự hào giới thiệu đến bạn nhiều trò chơi cá cược đặc sắc, bao gồm Baccarat trực tiếp, máy xèng, cá cược thể thao, xổ số và bắn cá, mang đến cho bạn cảm giác hồi hộp đỉnh cao của sòng bạc! Dù bạn yêu thích các trò chơi bài kinh điển hay những máy xèng đầy kịch tính, RGBET đều có thể đáp ứng mọi nhu cầu giải trí của bạn.
RGBET Trò Chơi của Chúng Tôi
Bạn đang tìm kiếm những trò chơi hot nhất và thú vị nhất tại sòng bạc trực tuyến? RGBET tự hào giới thiệu đến bạn nhiều trò chơi cá cược đặc sắc, bao gồm Baccarat trực tiếp, máy xèng, cá cược thể thao, xổ số và bắn cá, mang đến cảm giác hồi hộp đỉnh cao của sòng bạc! Dù bạn yêu thích các trò chơi bài kinh điển hay những máy xèng đầy kịch tính, RGBET đều có thể đáp ứng mọi nhu cầu giải trí của bạn.
RGBET Trò Chơi Đa Dạng
Thể thao: Cá cược thể thao đa dạng với nhiều môn từ bóng đá, tennis đến thể thao điện tử.
Live Casino: Trải nghiệm Baccarat, Roulette, và các trò chơi sòng bài trực tiếp với người chia bài thật.
Nổ hũ: Tham gia các trò chơi nổ hũ với tỷ lệ trúng cao và cơ hội thắng lớn.
Lô đề: Đặt cược lô đề với tỉ lệ cược hấp dẫn.
Bắn cá: Bắn cá RGBET mang đến cảm giác chân thực và hấp dẫn với đồ họa tuyệt đẹp.
RGBET – Máy Xèng Hấp Dẫn Nhất
Khám phá các máy xèng độc đáo tại RGBET với nhiều chủ đề khác nhau và tỷ lệ trả thưởng cao. Những trò chơi nổi bật bao gồm:
RGBET Super Ace
RGBET Đế Quốc Hoàng Kim
RGBET Pharaoh Treasure
RGBET Quyền Vương
RGBET Chuyên Gia Săn Rồng
RGBET Jackpot Fishing
Vì sao nên chọn RGBET?
RGBET không chỉ cung cấp hàng loạt trò chơi đa dạng mà còn mang đến một hệ thống cá cược an toàn và chuyên nghiệp, đảm bảo mọi quyền lợi của người chơi:
Tốc độ nạp tiền nhanh chóng: Chuyển khoản tại RGBET chỉ mất vài phút và tiền sẽ vào tài khoản ngay lập tức, giúp bạn không bỏ lỡ bất kỳ cơ hội nào.
Game đổi thưởng phong phú: Từ cá cược thể thao đến slot game, RGBET cung cấp đầy đủ trò chơi giúp bạn tận hưởng mọi phút giây thư giãn.
Bảo mật tuyệt đối: Với công nghệ mã hóa tiên tiến, tài khoản và tiền vốn của bạn sẽ luôn được bảo vệ một cách an toàn.
Hỗ trợ đa nền tảng: Bạn có thể chơi trên mọi thiết bị, từ máy tính, điện thoại di động (iOS/Android), đến nền tảng H5.
Tải Ứng Dụng RGBET và Nhận Khuyến Mãi Lớn
Hãy tham gia RGBET ngay hôm nay để tận hưởng thế giới giải trí không giới hạn với các trò chơi thể thao, thể thao điện tử, casino trực tuyến, xổ số, và slot game. Quét mã QR và tải ứng dụng RGBET trên điện thoại để trải nghiệm game tốt hơn và nhận nhiều khuyến mãi hấp dẫn!
Tham gia RGBET để bắt đầu cuộc hành trình cá cược đầy thú vị ngay hôm nay!
st666
ST666 – Nhà Cái Uy Tín Với Nhiều Khuyến Mãi Hấp Dẫn
ST666 là một trong những sòng bài trực tuyến uy tín nhất, mang đến cho các thành viên nhiều chương trình khuyến mãi đa dạng và hấp dẫn. Chúng tôi luôn hy vọng rằng những ưu đãi đặc biệt này sẽ mang lại trải nghiệm cá cược tuyệt vời cho tất cả thành viên của mình.
Khuyến Mãi Nạp Đầu Thưởng 100%
NO.1: Thưởng 100% lần nạp đầu tiên Thông thường, các khuyến mãi nạp tiền lần đầu đi kèm với yêu cầu vòng cược rất cao, thường từ 20 vòng trở lên. Tuy nhiên, ST666 hiểu rằng người chơi thường đắn đo khi quyết định nạp tiền vào sòng bài trực tuyến. Do đó, chúng tôi chỉ yêu cầu 8 vòng cược, cho phép người chơi rút tiền một cách nhanh chóng trong vòng 5 phút.
Thưởng 100% khi Đăng Nhập ST666
NO.2: Thưởng 16% mỗi ngày ST666 mang đến cho bạn một ưu đãi không thể bỏ lỡ. Mỗi khi bạn nạp tiền vào tài khoản hàng ngày, bạn sẽ được nhận thêm 16% số tiền nạp. Đây là cơ hội tuyệt vời dành cho những ai yêu thích cá cược trực tuyến và muốn gia tăng cơ hội chiến thắng của mình.
Bảo Hiểm Hoàn 10% Mỗi Ngày
NO.3: Bảo hiểm hoàn tiền 10% ST666 không chỉ hỗ trợ người chơi trong những lần may mắn mà còn luôn đồng hành khi bạn không gặp may. Chương trình khuyến mãi “bảo hiểm hoàn tiền 10% tổng tiền nạp mỗi ngày” là cách chúng tôi khích lệ và động viên tinh thần game thủ, giúp bạn tiếp tục hành trình chinh phục các thử thách cá cược.
Giới Thiệu Bạn Bè Thưởng 999K
NO.4: Giới thiệu bạn bè – Thưởng 999K Chương trình “Giới thiệu bạn bè” của ST666 giúp bạn có cơ hội cá cược cùng bạn bè và người thân. Không những vậy, bạn còn có thể nhận được phần thưởng lên đến 999K khi giới thiệu người bạn của mình tham gia ST666. Đây chính là một ưu đãi tuyệt vời giúp bạn vừa có thêm người đồng hành, vừa nhận được thưởng hấp dẫn.
Đăng Nhập Nhận Ngay 280K
NO.5: Điểm danh nhận thưởng 280K Nếu bạn là thành viên thường xuyên của ST666, hãy đừng quên nhấp vào hộp quà hàng ngày để điểm danh. Chỉ cần đăng nhập liên tục trong 7 ngày, cơ hội nhận thưởng 280K sẽ thuộc về bạn!
Kết Luận
ST666 luôn nỗ lực không ngừng để mang lại những chương trình khuyến mãi hấp dẫn và thiết thực nhất cho người chơi. Dù bạn là người mới hay đã gắn bó lâu năm với nền tảng, ST666 cam kết cung cấp trải nghiệm cá cược tốt nhất, an toàn và công bằng. Hãy tham gia ngay để không bỏ lỡ các cơ hội tuyệt vời từ ST666!
купить аттестат в твери купить аттестат в твери .
купить диплом психолога москва server-diploms.ru .
Приобретение школьного аттестата с официальным упрощенным обучением в Москве
купить диплом доставка man-diploms.ru .
Как купить диплом о высшем образовании с минимальными рисками
tihiy-don.su/2024/10/20/vash-diplom-bez-hlopot.html
Tether TRC20 Transaction Verification and AML (Anti-Money Laundering) Practices
As digital assets like Tether TRC20 rise in usage for fast and inexpensive payments, the need for protection and adherence with AML regulations expands. Here’s how to verify Tether TRON-based transfers and ensure they’re not linked to unlawful actions.
What is USDT TRC20?
TRON-based USDT is a digital currency on the TRON network, pegged in accordance with the American dollar. Known for its cheap transfers and velocity, it is frequently employed for international transactions. Checking transfers is important to prevent connections to illicit transfers or other criminal activities.
Verifying TRON-based USDT Payments
TRX Explorer — This blockchain viewer permits individuals to track and validate USDT TRC20 transactions using a wallet address or transfer code.
Supervising — Experienced players can track suspicious behaviors such as large or fast transactions to identify irregular actions.
AML and Criminal Crypto
AML (AML) rules help stop illicit financial activity in digital assets. Platforms like Chain Analysis and Elliptic enable companies and trading platforms to identify and stop criminal crypto, which signifies capital tied to illegal activities.
Solutions for Adherence
TRX Explorer — To validate USDT TRC20 transaction information.
Chainalysis and Elliptic — Employed by exchanges to guarantee AML adherence and follow unlawful operations.
Summary
Guaranteeing safe and legal TRON-based USDT transfers is critical. Services like TRONSCAN and Anti-Money Laundering solutions support guard participants from interacting with dirty cryptocurrency, promoting a secure and lawful crypto environment.
Полезные советы по безопасной покупке диплома о высшем образовании
Профессиональный сервисный центр по ремонту моноблоков iMac в Москве.
Мы предлагаем: ремонт imac с гарантией
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
вывод из запоя на дому ростов-на-дону вывод из запоя на дому ростов-на-дону .
Полезная информация на сайте. Все что вы хоте знать об интернете полезный сервис
Можно ли купить аттестат о среднем образовании? Основные рекомендации
order provigil 100mg sale – buy phenergan generic pill meloset 3mg
нью ретро казино нью ретро казино .
สล็อต888
สล็อต888 เป็นหนึ่งในแพลตฟอร์มเกมสล็อตออนไลน์ที่ได้รับความนิยมสูงสุดในปัจจุบัน โดยมีความโดดเด่นด้วยการให้บริการเกมสล็อตที่หลากหลายและมีคุณภาพ รวมถึงฟีเจอร์ที่ช่วยให้ผู้เล่นสามารถเพลิดเพลินกับการเล่นได้อย่างเต็มที่ ในบทความนี้ เราจะมาพูดถึงฟีเจอร์และจุดเด่นของสล็อต888 ที่ทำให้เว็บไซต์นี้ได้รับความนิยมเป็นอย่างมาก
ฟีเจอร์เด่นของ PG สล็อต888
ระบบฝากถอนเงินอัตโนมัติที่รวดเร็ว สล็อต888 ให้บริการระบบฝากถอนเงินแบบอัตโนมัติที่สามารถทำรายการได้ทันที ไม่ต้องรอนาน ไม่ว่าจะเป็นการฝากหรือถอนก็สามารถทำได้ภายในไม่กี่วินาที รองรับการใช้งานผ่านทรูวอลเล็ทและช่องทางอื่น ๆ โดยไม่มีขั้นต่ำในการฝากถอน
รองรับทุกอุปกรณ์ ทุกแพลตฟอร์ม ไม่ว่าคุณจะเล่นจากอุปกรณ์ใดก็ตาม สล็อต888 รองรับทั้งคอมพิวเตอร์ แท็บเล็ต และสมาร์ทโฟน ไม่ว่าจะเป็นระบบ iOS หรือ Android คุณสามารถเข้าถึงเกมสล็อตได้ทุกที่ทุกเวลาเพียงแค่มีอินเทอร์เน็ต
โปรโมชั่นและโบนัสมากมาย สำหรับผู้เล่นใหม่และลูกค้าประจำ สล็อต888 มีโปรโมชั่นต้อนรับ รวมถึงโบนัสพิเศษ เช่น ฟรีสปินและโบนัสเครดิตเพิ่ม ทำให้การเล่นเกมสล็อตกับเราเป็นเรื่องสนุกและมีโอกาสทำกำไรมากยิ่งขึ้น
ความปลอดภัยสูงสุด เรื่องความปลอดภัยเป็นสิ่งที่สล็อต888 ให้ความสำคัญเป็นอย่างยิ่ง เราใช้เทคโนโลยีการเข้ารหัสข้อมูลขั้นสูงเพื่อปกป้องข้อมูลส่วนบุคคลของลูกค้า ระบบฝากถอนเงินยังมีมาตรการรักษาความปลอดภัยที่เข้มงวด ทำให้ลูกค้ามั่นใจในการใช้บริการกับเรา
ทดลองเล่นสล็อตฟรี
สล็อต888 ยังมีบริการให้ผู้เล่นสามารถทดลองเล่นสล็อตได้ฟรี ซึ่งเป็นโอกาสที่ดีในการทดลองเล่นเกมต่าง ๆ ที่มีอยู่บนเว็บไซต์ เช่น Phoenix Rises, Dream Of Macau, Ways Of Qilin, Caishens Wins และเกมยอดนิยมอื่น ๆ ที่มีกราฟิกสวยงามและรูปแบบการเล่นที่น่าสนใจ
ไม่ว่าจะเป็นเกมแนวผจญภัย เช่น Rise Of Apollo, Dragon Hatch หรือเกมที่มีธีมแห่งความมั่งคั่งอย่าง Crypto Gold, Fortune Tiger, Lucky Piggy ทุกเกมได้รับการออกแบบมาเพื่อสร้างประสบการณ์การเล่นที่น่าจดจำและเต็มไปด้วยความสนุกสนาน
บทสรุป
สล็อต888 เป็นแพลตฟอร์มที่ครบเครื่องเรื่องเกมสล็อตออนไลน์ ด้วยฟีเจอร์ที่ทันสมัย โปรโมชั่นที่น่าสนใจ และระบบรักษาความปลอดภัยที่เข้มงวด ทำให้คุณมั่นใจได้ว่าการเล่นกับสล็อต888 จะเป็นประสบการณ์ที่ปลอดภัยและเต็มไปด้วยความสนุก
Всё о покупке аттестата о среднем образовании: полезные советы
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
tadalive.com/blog/366957/kupit-diplom-546453uvpt
Официальное получение диплома техникума с упрощенным обучением в Москве
вывод из запоя ростовская область http://www.vyvod-iz-zapoya-rostov117.ru .
crotamiton order online – how to get eurax without a prescription buy aczone paypal
USDT TRC20 Payment Check and Financial Crime Prevention (AML) Practices
As cryptocurrencies like Tether TRC20 gain popularity for fast and low-cost transfers, the demand for protection and conformance with financial crime prevention regulations grows. Here’s how to check USDT TRC20 payments and confirm they’re not linked to illegal actions.
What does it mean USDT TRC20?
TRON-based USDT is a digital currency on the TRX ledger, pegged in correspondence with the American dollar. Recognized for its minimal costs and velocity, it is commonly utilized for cross-border payments. Verifying transactions is essential to avoid links to illicit transfers or other criminal acts.
Verifying USDT TRC20 Transfers
TRX Explorer — This blockchain viewer permits individuals to monitor and validate Tether TRC20 transfers using a account ID or transfer code.
Tracking — Experienced users can track unusual patterns such as large or fast transfers to identify unusual behavior.
AML and Criminal Crypto
AML (AML) regulations support stop illegal financial activity in crypto markets. Platforms like Chainalysis and Elliptic allow enterprises and trading platforms to find and block criminal crypto, which means funds connected to unlawful operations.
Tools for Compliance
TRONSCAN — To check TRON-based USDT transfer data.
Chain Analysis and Elliptic — Utilized by exchanges to guarantee Anti-Money Laundering conformance and follow illegal actions.
Summary
Making sure secure and legitimate TRON-based USDT transfers is critical. Tools like TRX Explorer and AML tools assist shield participants from involving with criminal crypto, supporting a safe and lawful digital market.
Профессиональный сервисный центр по ремонту бытовой техники с выездом на дом.
Мы предлагаем: сервисные центры по ремонту техники в перми
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
เล่นบาคาร่าแบบรวดเร็วทันใจกับสปีดบาคาร่า
ถ้าคุณเป็นแฟนตัวยงของเกมไพ่บาคาร่า คุณอาจจะเคยชินกับการรอคอยในแต่ละรอบการเดิมพัน และรอจนดีลเลอร์แจกไพ่ในแต่ละตา แต่คุณรู้หรือไม่ว่า ตอนนี้คุณไม่ต้องรออีกต่อไปแล้ว เพราะ SA Gaming ได้พัฒนาเกมบาคาร่าโหมดใหม่ขึ้นมา เพื่อให้ประสบการณ์การเล่นของคุณน่าตื่นเต้นยิ่งขึ้น!
ที่ SA Gaming คุณสามารถเลือกเล่นไพ่บาคาร่าในโหมดที่เรียกว่า สปีดบาคาร่า (Speed Baccarat) โหมดนี้มีคุณสมบัติพิเศษและข้อดีที่น่าสนใจมากมาย:
ระยะเวลาการเดิมพันสั้นลง — คุณไม่จำเป็นต้องรอนานอีกต่อไป ในโหมดสปีดบาคาร่า คุณจะมีเวลาเพียง 12 วินาทีในการวางเดิมพัน ทำให้เกมแต่ละรอบจบได้รวดเร็ว โดยเกมในแต่ละรอบจะใช้เวลาเพียง 20 วินาทีเท่านั้น
ผลตอบแทนต่อผู้เล่นสูง (RTP) — เกมสปีดบาคาร่าให้ผลตอบแทนต่อผู้เล่นสูงถึง 4% ซึ่งเป็นมาตรฐานความเป็นธรรมที่ผู้เล่นสามารถไว้วางใจได้
การเล่นเกมที่รวดเร็วและน่าตื่นเต้น — ระยะเวลาที่สั้นลงทำให้เกมแต่ละรอบดำเนินไปอย่างรวดเร็ว ทันใจ เพิ่มความสนุกและความตื่นเต้นในการเล่น ทำให้ประสบการณ์การเล่นของคุณยิ่งสนุกมากขึ้น
กลไกและรูปแบบการเล่นยังคงเหมือนเดิม — แม้ว่าระยะเวลาจะสั้นลง แต่กลไกและกฎของการเล่น ยังคงเหมือนกับบาคาร่าสดปกติทุกประการ เพียงแค่ปรับเวลาให้เล่นได้รวดเร็วและสะดวกขึ้นเท่านั้น
นอกจากสปีดบาคาร่าแล้ว ที่ SA Gaming ยังมีโหมด No Commission Baccarat หรือบาคาร่าแบบไม่เสียค่าคอมมิชชั่น ซึ่งจะช่วยให้คุณสามารถเพลิดเพลินไปกับการเล่นได้โดยไม่ต้องกังวลเรื่องค่าคอมมิชชั่นเพิ่มเติม
เล่นบาคาร่ากับ SA Gaming คุณจะได้รับประสบการณ์การเล่นที่สนุก ทันสมัย และตรงใจมากที่สุด!
Быстрое обучение и получение диплома магистра – возможно ли это?
climat-cold.ru/forum/user/4169
Bạn đang tìm kiếm những trò chơi hot nhất và thú vị nhất tại sòng bạc trực tuyến? RGBET tự hào giới thiệu đến bạn nhiều trò chơi cá cược đặc sắc, bao gồm Baccarat trực tiếp, máy xèng, cá cược thể thao, xổ số và bắn cá, mang đến cho bạn cảm giác hồi hộp đỉnh cao của sòng bạc! Dù bạn yêu thích các trò chơi bài kinh điển hay những máy xèng đầy kịch tính, RGBET đều có thể đáp ứng mọi nhu cầu giải trí của bạn.
RGBET Trò Chơi của Chúng Tôi
Bạn đang tìm kiếm những trò chơi hot nhất và thú vị nhất tại sòng bạc trực tuyến? RGBET tự hào giới thiệu đến bạn nhiều trò chơi cá cược đặc sắc, bao gồm Baccarat trực tiếp, máy xèng, cá cược thể thao, xổ số và bắn cá, mang đến cảm giác hồi hộp đỉnh cao của sòng bạc! Dù bạn yêu thích các trò chơi bài kinh điển hay những máy xèng đầy kịch tính, RGBET đều có thể đáp ứng mọi nhu cầu giải trí của bạn.
RGBET Trò Chơi Đa Dạng
Thể thao: Cá cược thể thao đa dạng với nhiều môn từ bóng đá, tennis đến thể thao điện tử.
Live Casino: Trải nghiệm Baccarat, Roulette, và các trò chơi sòng bài trực tiếp với người chia bài thật.
Nổ hũ: Tham gia các trò chơi nổ hũ với tỷ lệ trúng cao và cơ hội thắng lớn.
Lô đề: Đặt cược lô đề với tỉ lệ cược hấp dẫn.
Bắn cá: Bắn cá RGBET mang đến cảm giác chân thực và hấp dẫn với đồ họa tuyệt đẹp.
RGBET – Máy Xèng Hấp Dẫn Nhất
Khám phá các máy xèng độc đáo tại RGBET với nhiều chủ đề khác nhau và tỷ lệ trả thưởng cao. Những trò chơi nổi bật bao gồm:
RGBET Super Ace
RGBET Đế Quốc Hoàng Kim
RGBET Pharaoh Treasure
RGBET Quyền Vương
RGBET Chuyên Gia Săn Rồng
RGBET Jackpot Fishing
Vì sao nên chọn RGBET?
RGBET không chỉ cung cấp hàng loạt trò chơi đa dạng mà còn mang đến một hệ thống cá cược an toàn và chuyên nghiệp, đảm bảo mọi quyền lợi của người chơi:
Tốc độ nạp tiền nhanh chóng: Chuyển khoản tại RGBET chỉ mất vài phút và tiền sẽ vào tài khoản ngay lập tức, giúp bạn không bỏ lỡ bất kỳ cơ hội nào.
Game đổi thưởng phong phú: Từ cá cược thể thao đến slot game, RGBET cung cấp đầy đủ trò chơi giúp bạn tận hưởng mọi phút giây thư giãn.
Bảo mật tuyệt đối: Với công nghệ mã hóa tiên tiến, tài khoản và tiền vốn của bạn sẽ luôn được bảo vệ một cách an toàn.
Hỗ trợ đa nền tảng: Bạn có thể chơi trên mọi thiết bị, từ máy tính, điện thoại di động (iOS/Android), đến nền tảng H5.
Tải Ứng Dụng RGBET và Nhận Khuyến Mãi Lớn
Hãy tham gia RGBET ngay hôm nay để tận hưởng thế giới giải trí không giới hạn với các trò chơi thể thao, thể thao điện tử, casino trực tuyến, xổ số, và slot game. Quét mã QR và tải ứng dụng RGBET trên điện thoại để trải nghiệm game tốt hơn và nhận nhiều khuyến mãi hấp dẫn!
Tham gia RGBET để bắt đầu cuộc hành trình cá cược đầy thú vị ngay hôm nay!
Быстрое обучение и получение диплома магистра – возможно ли это?
new retro казино http://newretrocasino-casino3.ru .
เกมบาคาร่า
เล่นบาคาร่าแบบรวดเร็วทันใจกับสปีดบาคาร่า
ถ้าคุณเป็นแฟนตัวยงของเกมไพ่บาคาร่า คุณอาจจะเคยชินกับการรอคอยในแต่ละรอบการเดิมพัน และรอจนดีลเลอร์แจกไพ่ในแต่ละตา แต่คุณรู้หรือไม่ว่า ตอนนี้คุณไม่ต้องรออีกต่อไปแล้ว เพราะ SA Gaming ได้พัฒนาเกมบาคาร่าโหมดใหม่ขึ้นมา เพื่อให้ประสบการณ์การเล่นของคุณน่าตื่นเต้นยิ่งขึ้น!
ที่ SA Gaming คุณสามารถเลือกเล่นไพ่บาคาร่าในโหมดที่เรียกว่า สปีดบาคาร่า (Speed Baccarat) โหมดนี้มีคุณสมบัติพิเศษและข้อดีที่น่าสนใจมากมาย:
ระยะเวลาการเดิมพันสั้นลง — คุณไม่จำเป็นต้องรอนานอีกต่อไป ในโหมดสปีดบาคาร่า คุณจะมีเวลาเพียง 12 วินาทีในการวางเดิมพัน ทำให้เกมแต่ละรอบจบได้รวดเร็ว โดยเกมในแต่ละรอบจะใช้เวลาเพียง 20 วินาทีเท่านั้น
ผลตอบแทนต่อผู้เล่นสูง (RTP) — เกมสปีดบาคาร่าให้ผลตอบแทนต่อผู้เล่นสูงถึง 4% ซึ่งเป็นมาตรฐานความเป็นธรรมที่ผู้เล่นสามารถไว้วางใจได้
การเล่นเกมที่รวดเร็วและน่าตื่นเต้น — ระยะเวลาที่สั้นลงทำให้เกมแต่ละรอบดำเนินไปอย่างรวดเร็ว ทันใจ เพิ่มความสนุกและความตื่นเต้นในการเล่น ทำให้ประสบการณ์การเล่นของคุณยิ่งสนุกมากขึ้น
กลไกและรูปแบบการเล่นยังคงเหมือนเดิม — แม้ว่าระยะเวลาจะสั้นลง แต่กลไกและกฎของการเล่น ยังคงเหมือนกับบาคาร่าสดปกติทุกประการ เพียงแค่ปรับเวลาให้เล่นได้รวดเร็วและสะดวกขึ้นเท่านั้น
นอกจากสปีดบาคาร่าแล้ว ที่ SA Gaming ยังมีโหมด No Commission Baccarat หรือบาคาร่าแบบไม่เสียค่าคอมมิชชั่น ซึ่งจะช่วยให้คุณสามารถเพลิดเพลินไปกับการเล่นได้โดยไม่ต้องกังวลเรื่องค่าคอมมิชชั่นเพิ่มเติม
เล่นบาคาร่ากับ SA Gaming คุณจะได้รับประสบการณ์การเล่นที่สนุก ทันสมัย และตรงใจมากที่สุด!
download instagram stories download instagram stories .
где купить диплом в рязани landik-diploms.ru .
ST666 – Nhà Cái Uy Tín Với Nhiều Khuyến Mãi Hấp Dẫn
ST666 là một trong những sòng bài trực tuyến uy tín nhất, mang đến cho các thành viên nhiều chương trình khuyến mãi đa dạng và hấp dẫn. Chúng tôi luôn hy vọng rằng những ưu đãi đặc biệt này sẽ mang lại trải nghiệm cá cược tuyệt vời cho tất cả thành viên của mình.
Khuyến Mãi Nạp Đầu Thưởng 100%
NO.1: Thưởng 100% lần nạp đầu tiên Thông thường, các khuyến mãi nạp tiền lần đầu đi kèm với yêu cầu vòng cược rất cao, thường từ 20 vòng trở lên. Tuy nhiên, ST666 hiểu rằng người chơi thường đắn đo khi quyết định nạp tiền vào sòng bài trực tuyến. Do đó, chúng tôi chỉ yêu cầu 8 vòng cược, cho phép người chơi rút tiền một cách nhanh chóng trong vòng 5 phút.
Thưởng 100% khi Đăng Nhập ST666
NO.2: Thưởng 16% mỗi ngày ST666 mang đến cho bạn một ưu đãi không thể bỏ lỡ. Mỗi khi bạn nạp tiền vào tài khoản hàng ngày, bạn sẽ được nhận thêm 16% số tiền nạp. Đây là cơ hội tuyệt vời dành cho những ai yêu thích cá cược trực tuyến và muốn gia tăng cơ hội chiến thắng của mình.
Bảo Hiểm Hoàn 10% Mỗi Ngày
NO.3: Bảo hiểm hoàn tiền 10% ST666 không chỉ hỗ trợ người chơi trong những lần may mắn mà còn luôn đồng hành khi bạn không gặp may. Chương trình khuyến mãi “bảo hiểm hoàn tiền 10% tổng tiền nạp mỗi ngày” là cách chúng tôi khích lệ và động viên tinh thần game thủ, giúp bạn tiếp tục hành trình chinh phục các thử thách cá cược.
Giới Thiệu Bạn Bè Thưởng 999K
NO.4: Giới thiệu bạn bè – Thưởng 999K Chương trình “Giới thiệu bạn bè” của ST666 giúp bạn có cơ hội cá cược cùng bạn bè và người thân. Không những vậy, bạn còn có thể nhận được phần thưởng lên đến 999K khi giới thiệu người bạn của mình tham gia ST666. Đây chính là một ưu đãi tuyệt vời giúp bạn vừa có thêm người đồng hành, vừa nhận được thưởng hấp dẫn.
Đăng Nhập Nhận Ngay 280K
NO.5: Điểm danh nhận thưởng 280K Nếu bạn là thành viên thường xuyên của ST666, hãy đừng quên nhấp vào hộp quà hàng ngày để điểm danh. Chỉ cần đăng nhập liên tục trong 7 ngày, cơ hội nhận thưởng 280K sẽ thuộc về bạn!
Kết Luận
ST666 luôn nỗ lực không ngừng để mang lại những chương trình khuyến mãi hấp dẫn và thiết thực nhất cho người chơi. Dù bạn là người mới hay đã gắn bó lâu năm với nền tảng, ST666 cam kết cung cấp trải nghiệm cá cược tốt nhất, an toàn và công bằng. Hãy tham gia ngay để không bỏ lỡ các cơ hội tuyệt vời từ ST666!
instagram profile instagram profile .
Пошаговая инструкция по официальной покупке диплома о высшем образовании
Реально ли приобрести диплом стоматолога? Основные этапы
купить диплом ссср а высшем цена prema-diploms.ru .
เกมบาคาร่า
เล่นบาคาร่าแบบรวดเร็วทันใจกับสปีดบาคาร่า
ถ้าคุณเป็นแฟนตัวยงของเกมไพ่บาคาร่า คุณอาจจะเคยชินกับการรอคอยในแต่ละรอบการเดิมพัน และรอจนดีลเลอร์แจกไพ่ในแต่ละตา แต่คุณรู้หรือไม่ว่า ตอนนี้คุณไม่ต้องรออีกต่อไปแล้ว เพราะ SA Gaming ได้พัฒนาเกมบาคาร่าโหมดใหม่ขึ้นมา เพื่อให้ประสบการณ์การเล่นของคุณน่าตื่นเต้นยิ่งขึ้น!
ที่ SA Gaming คุณสามารถเลือกเล่นไพ่บาคาร่าในโหมดที่เรียกว่า สปีดบาคาร่า (Speed Baccarat) โหมดนี้มีคุณสมบัติพิเศษและข้อดีที่น่าสนใจมากมาย:
ระยะเวลาการเดิมพันสั้นลง — คุณไม่จำเป็นต้องรอนานอีกต่อไป ในโหมดสปีดบาคาร่า คุณจะมีเวลาเพียง 12 วินาทีในการวางเดิมพัน ทำให้เกมแต่ละรอบจบได้รวดเร็ว โดยเกมในแต่ละรอบจะใช้เวลาเพียง 20 วินาทีเท่านั้น
ผลตอบแทนต่อผู้เล่นสูง (RTP) — เกมสปีดบาคาร่าให้ผลตอบแทนต่อผู้เล่นสูงถึง 4% ซึ่งเป็นมาตรฐานความเป็นธรรมที่ผู้เล่นสามารถไว้วางใจได้
การเล่นเกมที่รวดเร็วและน่าตื่นเต้น — ระยะเวลาที่สั้นลงทำให้เกมแต่ละรอบดำเนินไปอย่างรวดเร็ว ทันใจ เพิ่มความสนุกและความตื่นเต้นในการเล่น ทำให้ประสบการณ์การเล่นของคุณยิ่งสนุกมากขึ้น
กลไกและรูปแบบการเล่นยังคงเหมือนเดิม — แม้ว่าระยะเวลาจะสั้นลง แต่กลไกและกฎของการเล่น ยังคงเหมือนกับบาคาร่าสดปกติทุกประการ เพียงแค่ปรับเวลาให้เล่นได้รวดเร็วและสะดวกขึ้นเท่านั้น
นอกจากสปีดบาคาร่าแล้ว ที่ SA Gaming ยังมีโหมด No Commission Baccarat หรือบาคาร่าแบบไม่เสียค่าคอมมิชชั่น ซึ่งจะช่วยให้คุณสามารถเพลิดเพลินไปกับการเล่นได้โดยไม่ต้องกังวลเรื่องค่าคอมมิชชั่นเพิ่มเติม
เล่นบาคาร่ากับ SA Gaming คุณจะได้รับประสบการณ์การเล่นที่สนุก ทันสมัย และตรงใจมากที่สุด!
USDT TRON-based Transaction Check and Financial Crime Prevention (AML) Methods
As digital assets like USDT TRON-based increase in popularity for fast and affordable payments, the requirement for security and compliance with AML regulations increases. Here’s how to review Tether TRC20 payments and guarantee they’re not related to unlawful operations.
What is TRON-based USDT?
TRON-based USDT is a stablecoin on the TRON network, pegged in accordance with the USD. Recognized for its minimal costs and velocity, it is commonly utilized for international payments. Checking transactions is crucial to avoid links to money laundering or other illegal acts.
Checking USDT TRC20 Payments
TRONSCAN — This blockchain viewer enables individuals to track and check Tether TRON-based transfers using a public address or transaction ID.
Supervising — Experienced users can track anomalous patterns such as high-volume or quick transactions to identify unusual behavior.
AML and Illicit Funds
AML (AML) rules assist block illicit financial activity in cryptocurrency. Platforms like Chain Analysis and Elliptic allow enterprises and trading platforms to detect and stop illicit funds, which refers to money related to criminal actions.
Solutions for Adherence
TRX Explorer — To verify TRON-based USDT payment details.
Chain Analysis and Elliptic Solutions — Used by trading platforms to ensure Anti-Money Laundering conformance and track illicit activities.
Conclusion
Making sure secure and legal USDT TRC20 payments is critical. Platforms like TRONSCAN and Anti-Money Laundering tools support guard traders from engaging with criminal crypto, supporting a secure and regulated cryptocurrency space.
диплом на заказ server-diploms.ru .
Официальная покупка аттестата о среднем образовании в Москве и других городах
Рекомендации по безопасной покупке диплома о высшем образовании
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
Как купить диплом о высшем образовании с минимальными рисками
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
купить диплом в москве о высшем образовании купить диплом в москве о высшем образовании .
Сломался телефон, думал покупать новый, но решил попробовать отремонтировать. Обратился в этот сервисный центр и не пожалел. Профессионалы своего дела быстро восстановили мой телефон. Рекомендую посетить их сайт: ремонт сенсорных телефонов.
пансионат для пожилых с альцгеймера пансионат для пожилых с альцгеймера .
Всё, что нужно знать о покупке аттестата о среднем образовании
sharecovid19story.com/viewtopic.php?t=1258891
Официальная покупка аттестата о среднем образовании в Москве и других городах
mediasafar.com/create-blog/
Профессиональный сервисный центр по ремонту компьютеров и ноутбуков в Москве.
Мы предлагаем: ремонт мак в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
заказать диплом russa-diploms.ru .
купить диплом о среднем специальном образовании в москве купить диплом о среднем специальном образовании в москве .
можно купить диплом врача orik-diploms.ru .
Всё о покупке аттестата о среднем образовании: полезные советы
Сервисный центр предлагает ремонт материнских плат ecs в москве центр ремонта материнской платы ecs
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
купить программу 1с торговля купить программу 1с торговля .
Легальные способы покупки диплома о среднем полном образовании
Официальная покупка диплома вуза с сокращенной программой в Москве
tadalive.com/blog/370623/kupit-diplom-360231viol
пансионат для престарелых в береговом http://xn—–6kcacwibu7aeobnlkrcglni7eyhud.xn--p1ai .
дом престарелых в любимовке дом престарелых в любимовке .
вывод из запоя в наркологическом стационаре https://vyvod-iz-zapoya-sochi15.ru/ .
RGBET Trang Chủ Và Câu Chuyện Thương Hiệu
Ra đời vào năm 2010 tại Đài Loan, RGBET nhanh chóng trở thành một trang cá cược chất lượng hàng đầu khu vực Châu Á. Nhà cái được cấp phép hoạt động hợp pháp bởi công ty giải trí trực tuyến hợp pháp được ủy quyền và giám sát theo giấy phép Malta của Châu Âu – MGA. Và chịu sự giám sát chặt chẽ của tổ chức PAGCOR và BIV.
RGBET trang chủ cung cấp cho người chơi đa dạng các thể loại cược đặc sắc như: thể thao, đá gà, xổ số, nổ hũ, casino trực tuyến. Dịch vụ CSKH luôn hoạt động 24/7. Với chứng chỉ công nghệ GEOTRUST, nhà cái đảm bảo an toàn cho mọi giao dịch của khách hàng. APP RG thiết kế tối ưu giải quyết mọi vấn đề của người dùng IOS và Android.
Là một nhà cái đến từ đất nước công nghệ, nhà cái luôn không ngừng xây dựng và nâng cấp hệ thống game và dịch vụ hoàn hảo. Mọi giao dịch nạp rút được tự động hoá cho phép người chơi hoàn tất giao dịch chỉ với 2 phút vô cùng nhanh chóng
RGBET Lớn Nhất Uy Tín Nhất – Giá Trị Cốt Lõi
Nhà Cái RG Và Mục Tiêu Thương Hiệu
Giá trị cốt lõi mà RGBET mong muốn hướng đến đó chính là không ngừng hoàn thiện để đem đến một hệ thống chất lượng, công bằng và an toàn. Nâng cao sự hài lòng của người chơi, đẩy mạnh hoạt động chống gian lận và lừa đảo. RG luôn cung cấp hệ thống kèo nhà cái đặc sắc, cùng các sự kiện – giải đấu hàng đầu và tỷ lệ cược cạnh tranh đáp ứng mọi nhu cầu khách hàng.
Thương hiệu cá cược RGBET cam kết đem lại cho người chơi môi trường cá cược công bằng, văn minh và lành mạnh. Đây là nguồn động lực to lớn giúp nhà cái thực tế hóa các hoạt động của mình.
RGBET Có Tầm Nhìn Và Sứ Mệnh
Đổi mới và sáng tạo là yếu tố cốt lõi giúp đạt được mục tiêu dưới sự chuyển mình mạnh mẽ của công nghệ. Tầm nhìn và sứ mệnh của RGBET là luôn tìm tòi những điều mới lạ, đột phá mạnh mẽ, vượt khỏi giới hạn bản thân, đương đầu với thử thách để đem đến cho khách hàng sản phẩm hoàn thiện nhất.
Chúng tôi luôn sẵn sàng tiếp thu ý kiến và nâng cao bản thân mỗi ngày để tạo ra sân chơi bổ ích, uy tín và chuyên nghiệp cho người chơi. Để có thể trở thành nhà cái phù hợp với mọi khách hàng.
Khái Niệm Giá Trị Cốt Lõi Nhà Cái RGBET
Giá trị cốt lõi của nhà cái RG luôn gắn kết chặt chẽ với nhau giữa 5 khái niệm: Chính trực, chuyên nghiệp, an toàn, đổi mới, công nghệ.
Chính Trực
Mọi quy luật, cách thức của trò chơi đều được nhà cái cung cấp công khai, minh bạch và chi tiết. Mỗi tựa game hoạt động đều phải chịu sự giám sát kỹ lưỡng bởi các cơ quan tổ chức có tiếng về sự an toàn và minh bạch của nó.
Chuyên Nghiệp
Các hoạt động tại RGBET trang chủ luôn đề cao sự chuyên nghiệp lên hàng đầu. Từ giao diện đến chất lượng sản phẩm luôn được trau chuốt tỉ mỉ từng chi tiết. Thế giới giải trí được xây dựng theo văn hóa Châu Á, phù hợp với đại đa số thị phần khách Việt.
An Toàn
RG lớn nhất uy tín nhất luôn ưu tiên sử dụng công nghệ mã hóa hiện đại nhất để đảm bảo an toàn, riêng tư cho toàn bộ thông tin của người chơi. Đơn vị cam kết nói không với hành vi gian lận và mua bán, trao đổi thông tin cá nhân bất hợp pháp.
Đổi Mới
Nhà cái luôn theo dõi và bắt kịp xu hướng thời đại, liên tục bổ sung các sản phẩm mới, phương thức cá cược mới và các ưu đãi độc lạ, mang đến những trải nghiệm thú vị cho người chơi.
Công Nghệ
RGBET trang chủ tập trung xây dựng một giao diện game sắc nét, sống động cùng tốc độ tải nhanh chóng. Ứng dụng RGBET giải nén ít dung lượng phù hợp với mọi hệ điều hành và cấu hình, tăng khả năng sử dụng của khách hàng.
RGBET Khẳng Định Giá Trị Thương Hiệu
Hoạt động hợp pháp với đầy đủ giấy phép, chứng chỉ an toàn đạt tiêu chuẩn quốc tế
Hệ thống game đa màu sắc, đáp ứng được mọi nhu cầu người chơi
Chính sách bảo mật RG hiện đại và đảm bảo an toàn cho người chơi cá cược
Bắt tay hợp tác với nhiều đơn vị phát hành game uy tín, chất lượng thế giới
Giao dịch nạp rút RG cấp tốc, nhanh gọn, bảo mật an toàn
Kèo nhà cái đa dạng với bảng tỷ lệ kèo cao, hấp dẫn
Dịch Vụ RGBET Casino Online
Dịch vụ khách hàng
Đội ngũ CSKH RGBET luôn hoạt động thường trực 24/7. Nhân viên được đào tạo chuyên sâu luôn giải đáp tất cả các khó khăn của người chơi về các vấn đề tài khoản, khuyến mãi, giao dịch một cách nhanh chóng và chuẩn xác. Hạn chế tối đa làm ảnh hưởng đến quá trình trải nghiệm của khách hàng.
Đa dạng trò chơi
Với sự nhạy bén trong cập nhật xu thế, nhà cái RGBET đã dành nhiều thời gian phân tích nhu cầu khách hàng, đem đến một kho tàng game chất lượng với đa dạng thể loại từ RG casino online, thể thao, nổ hũ, game bài, đá gà, xổ số.
Khuyến mãi hấp dẫn
RGBET trang chủ liên tục cập nhật và thay đổi các sự kiện ưu đãi đầy hấp dẫn và độc đáo. Mọi thành viên bất kể là người chơi mới, người chơi cũ hay hội viên VIP đều có cơ hội được hưởng ưu đãi đặc biệt từ nhà cái.
Giao dịch linh hoạt, tốc độ
Thương hiệu RGBET luôn chú tâm đến hệ thống giao dịch. Nhà cái cung cấp dịch vụ nạp rút nhanh chóng với đa dạng phương thức như thẻ cào, ví điện tử, ngân hàng điện tử, ngân hàng trực tiếp. Mọi hoạt động đều được bảo mật tuyệt đối bởi công nghệ mã hóa tiên tiến.
App cá độ RGBET
App cá độ RGBET là một ứng dụng cho phép người chơi đăng nhập RG nhanh chóng, đồng thời các thao tác đăng ký RG trên app cũng được tối ưu và trở nên đơn giản hơn. Tham gia cá cược RG bằng app cá độ, người chơi sẽ có 1 trải nghiệm cá cược tuyệt vời và thú vị.
RGBET Có Chứng Nhận Cá Cược Quốc Tế
Nhà cái RGBET hoạt động hợp pháp dưới sự cấp phép của hai tổ chức thế giới là PAGCOR và MGA, tính minh bạch và công bằng luôn được giám sát gắt gao bởi BIV. Khi tham gia cược tại đây, người chơi sẽ được đảm bảo quyền và lợi ích hợp pháp của mình.
Việc sở hữu các chứng nhận quốc tế còn cho thấy nguồn tài chính ổn định, dồi dào của RGBET. Điều này cho thấy việc một nhà cái được công nhận bởi các cơ quan quốc tế không phải là một chuyện dễ.
Theo quy định nhà cái RGBET, chỉ người chơi từ đủ 18 tuổi trở lên mới có thể tham gia cá cược tại RGBET
MGA (Malta Gaming Authority)
Tổ chức MGA đảm bảo tính vẹn toàn và ổn định của các trò chơi. Có các chính sách bảo vệ nguồn tài chính và quyền lợi của người chơi. Chứng nhận một nhà cái hoạt động có đầy đủ pháp lý, tuân thủ nghiêm chỉnh luật cờ bạc.
Chứng nhận Quần đảo Virgin Vương quốc Anh (BIV)
Tổ chứng chứng nhận nhà cái có đầy đủ tài chính để hoạt động kinh doanh cá cược. Với nguồn ngân sách dồi dào, ổn định nhà cái bảo đảm tính thanh khoản cho người chơi, mọi quyền lợi sẽ không bị xâm phạm.
Giấy Phép PAGCOR
Tổ chức cấp giấy phép cho nhà cái hoạt động đạt chuẩn theo tiêu chuẩn quốc tế. Cho phép nhà cái tổ chức cá cược một cách hợp pháp, không bị rào cản. Có chính sách ngăn chặn mọi trò chơi có dấu hiệu lừa đảo, duy trì sự minh bạch, công bằng.
Nhà Cái RGBET Phát Triển Công Nghệ
Nhà cái RGBET hỗ trợ trên nhiều thiết bị : IOS, Android, APP, WEB, Html5
RG và Trách Nhiệm Xã Hội
RGBET RichGame không đơn thuần là một trang cá cược giải trí mà nhà cái còn thể hiện rõ tính trách nhiệm xã hội của mình. Đơn vị luôn mong muốn người chơi tham gia cá cược phải có trách nhiệm với bản thân, gia đình và cả xã hội. Mọi hoạt động diễn ra tại RGBET trang chủ nói riêng hay bất kỳ trang web khác, người chơi phải thật sự bình tĩnh và lý trí, đừng để bản thân rơi vào “cạm bẫy của cờ bạc”.
RGBET RichGame với chính sách nghiêm cấm mọi hành vi xâm phạm thông tin cá nhân và gian lận nhằm tạo ra một môi trường cá cược công bằng, lành mạnh. Nhà cái khuyến cáo mọi cá nhân chưa đủ 18 tuổi không nên đăng ký RG và tham gia vào bất kỳ hoạt động cá cược nào.
sa gaming
ค่าย SA Gaming เป็น บริษัท เกม บาคาร่า ออนไลน์ ที่ได้รับการยอมรับ ใน ระดับสากล ว่าเป็น เจ้าตลาด ในการให้บริการ บริการ คาสิโนออนไลน์ โดยเฉพาะในด้าน เกมไพ่ บาคาร่า ซึ่งเป็น เกม ที่ ผู้คน สนใจเล่นกัน อย่างกว้างขวาง ใน คาสิโนจริง และ ออนไลน์ ด้วย รูปแบบการเล่น ที่ ง่าย การเลือกเดิมพัน เพียง ฝั่ง ฝั่งผู้เล่น หรือ แบงค์เกอร์ และ เปอร์เซ็นต์การชนะ ที่ ค่อนข้างสูง ทำให้ เกมพนันบาคาร่า ได้รับ ความสนใจ อย่างมากใน ช่วงหลายปีที่ผ่านมา โดยเฉพาะใน บ้านเรา
หนึ่งในรูปแบบการเล่น ยอดนิยมที่ SA Gaming นำเสนอ คือ สปีดบาคาร่า ซึ่ง ให้โอกาสผู้เล่นที่ ต้องการ ความรวดเร็ว และ การคิดไว สามารถ เดิมพันได้อย่างรวดเร็ว นอกจากนี้ยังมีโหมด ไม่มีค่าคอมมิชชั่น ซึ่งเป็น แบบ ที่ ไม่มีค่าคอมมิชชั่นเพิ่ม เมื่อชนะ การแทง ฝั่งเจ้ามือ ทำให้ โหมดนี้ ได้รับ ความคุ้มค่า จาก ผู้เล่น ที่มองหา ผลประโยชน์ ในการ เดิมพัน
เกมไพ่พนัน ของ เอสเอ เกมมิ่ง ยัง ถูกพัฒนา ให้มี กราฟฟิค ร่วมกับ ระบบเสียง ที่ สมจริง จำลองบรรยากาศ ที่ น่าตื่นเต้น เหมือนอยู่ใน คาสิโนใหญ่ พร้อมกับ ฟังก์ชัน ที่ทำให้ ผู้เล่น สามารถเลือก วิธีแทง ที่ แตกต่างกัน ไม่ว่าจะเป็น การเดิมพัน ตามกลยุทธ์ ของตน หรือการ ใช้กลยุทธ์ ให้ชนะ นอกจากนี้ยังมี ดีลเลอร์ไลฟ์ ที่ ควบคุมเกม ในแต่ละ ห้อง ทำให้ เกม มี ความน่าสนใจ มากยิ่งขึ้น
ด้วย ความยืดหยุ่น ใน การเสี่ยงโชค และ การเล่นที่ง่าย ในการ เล่น เอสเอ เกมมิ่ง ได้ สร้างสรรค์ เกมไพ่ ที่ เหมาะสมกับ ทุก กลุ่ม ของผู้เล่น ตั้งแต่ ผู้เล่นมือใหม่ ไปจนถึง นักเดิมพัน มืออาชีพ
Всё, что нужно знать о покупке аттестата о среднем образовании
сервис ремонт телефонов
Вопросы и ответы: можно ли быстро купить диплом старого образца?
1001viktorina.ru/forum/viewtopic.php?f=19&t=1724&sid=6b18cfc2323e9afa70c7b68a3dce8207
RGBET Trang Chủ Và Câu Chuyện Thương Hiệu
Ra đời vào năm 2010 tại Đài Loan, RGBET nhanh chóng trở thành một trang cá cược chất lượng hàng đầu khu vực Châu Á. Nhà cái được cấp phép hoạt động hợp pháp bởi công ty giải trí trực tuyến hợp pháp được ủy quyền và giám sát theo giấy phép Malta của Châu Âu – MGA. Và chịu sự giám sát chặt chẽ của tổ chức PAGCOR và BIV.
RGBET trang chủ cung cấp cho người chơi đa dạng các thể loại cược đặc sắc như: thể thao, đá gà, xổ số, nổ hũ, casino trực tuyến. Dịch vụ CSKH luôn hoạt động 24/7. Với chứng chỉ công nghệ GEOTRUST, nhà cái đảm bảo an toàn cho mọi giao dịch của khách hàng. APP RG thiết kế tối ưu giải quyết mọi vấn đề của người dùng IOS và Android.
Là một nhà cái đến từ đất nước công nghệ, nhà cái luôn không ngừng xây dựng và nâng cấp hệ thống game và dịch vụ hoàn hảo. Mọi giao dịch nạp rút được tự động hoá cho phép người chơi hoàn tất giao dịch chỉ với 2 phút vô cùng nhanh chóng
RGBET Lớn Nhất Uy Tín Nhất – Giá Trị Cốt Lõi
Nhà Cái RG Và Mục Tiêu Thương Hiệu
Giá trị cốt lõi mà RGBET mong muốn hướng đến đó chính là không ngừng hoàn thiện để đem đến một hệ thống chất lượng, công bằng và an toàn. Nâng cao sự hài lòng của người chơi, đẩy mạnh hoạt động chống gian lận và lừa đảo. RG luôn cung cấp hệ thống kèo nhà cái đặc sắc, cùng các sự kiện – giải đấu hàng đầu và tỷ lệ cược cạnh tranh đáp ứng mọi nhu cầu khách hàng.
Thương hiệu cá cược RGBET cam kết đem lại cho người chơi môi trường cá cược công bằng, văn minh và lành mạnh. Đây là nguồn động lực to lớn giúp nhà cái thực tế hóa các hoạt động của mình.
RGBET Có Tầm Nhìn Và Sứ Mệnh
Đổi mới và sáng tạo là yếu tố cốt lõi giúp đạt được mục tiêu dưới sự chuyển mình mạnh mẽ của công nghệ. Tầm nhìn và sứ mệnh của RGBET là luôn tìm tòi những điều mới lạ, đột phá mạnh mẽ, vượt khỏi giới hạn bản thân, đương đầu với thử thách để đem đến cho khách hàng sản phẩm hoàn thiện nhất.
Chúng tôi luôn sẵn sàng tiếp thu ý kiến và nâng cao bản thân mỗi ngày để tạo ra sân chơi bổ ích, uy tín và chuyên nghiệp cho người chơi. Để có thể trở thành nhà cái phù hợp với mọi khách hàng.
Khái Niệm Giá Trị Cốt Lõi Nhà Cái RGBET
Giá trị cốt lõi của nhà cái RG luôn gắn kết chặt chẽ với nhau giữa 5 khái niệm: Chính trực, chuyên nghiệp, an toàn, đổi mới, công nghệ.
Chính Trực
Mọi quy luật, cách thức của trò chơi đều được nhà cái cung cấp công khai, minh bạch và chi tiết. Mỗi tựa game hoạt động đều phải chịu sự giám sát kỹ lưỡng bởi các cơ quan tổ chức có tiếng về sự an toàn và minh bạch của nó.
Chuyên Nghiệp
Các hoạt động tại RGBET trang chủ luôn đề cao sự chuyên nghiệp lên hàng đầu. Từ giao diện đến chất lượng sản phẩm luôn được trau chuốt tỉ mỉ từng chi tiết. Thế giới giải trí được xây dựng theo văn hóa Châu Á, phù hợp với đại đa số thị phần khách Việt.
An Toàn
RG lớn nhất uy tín nhất luôn ưu tiên sử dụng công nghệ mã hóa hiện đại nhất để đảm bảo an toàn, riêng tư cho toàn bộ thông tin của người chơi. Đơn vị cam kết nói không với hành vi gian lận và mua bán, trao đổi thông tin cá nhân bất hợp pháp.
Đổi Mới
Nhà cái luôn theo dõi và bắt kịp xu hướng thời đại, liên tục bổ sung các sản phẩm mới, phương thức cá cược mới và các ưu đãi độc lạ, mang đến những trải nghiệm thú vị cho người chơi.
Công Nghệ
RGBET trang chủ tập trung xây dựng một giao diện game sắc nét, sống động cùng tốc độ tải nhanh chóng. Ứng dụng RGBET giải nén ít dung lượng phù hợp với mọi hệ điều hành và cấu hình, tăng khả năng sử dụng của khách hàng.
RGBET Khẳng Định Giá Trị Thương Hiệu
Hoạt động hợp pháp với đầy đủ giấy phép, chứng chỉ an toàn đạt tiêu chuẩn quốc tế
Hệ thống game đa màu sắc, đáp ứng được mọi nhu cầu người chơi
Chính sách bảo mật RG hiện đại và đảm bảo an toàn cho người chơi cá cược
Bắt tay hợp tác với nhiều đơn vị phát hành game uy tín, chất lượng thế giới
Giao dịch nạp rút RG cấp tốc, nhanh gọn, bảo mật an toàn
Kèo nhà cái đa dạng với bảng tỷ lệ kèo cao, hấp dẫn
Dịch Vụ RGBET Casino Online
Dịch vụ khách hàng
Đội ngũ CSKH RGBET luôn hoạt động thường trực 24/7. Nhân viên được đào tạo chuyên sâu luôn giải đáp tất cả các khó khăn của người chơi về các vấn đề tài khoản, khuyến mãi, giao dịch một cách nhanh chóng và chuẩn xác. Hạn chế tối đa làm ảnh hưởng đến quá trình trải nghiệm của khách hàng.
Đa dạng trò chơi
Với sự nhạy bén trong cập nhật xu thế, nhà cái RGBET đã dành nhiều thời gian phân tích nhu cầu khách hàng, đem đến một kho tàng game chất lượng với đa dạng thể loại từ RG casino online, thể thao, nổ hũ, game bài, đá gà, xổ số.
Khuyến mãi hấp dẫn
RGBET trang chủ liên tục cập nhật và thay đổi các sự kiện ưu đãi đầy hấp dẫn và độc đáo. Mọi thành viên bất kể là người chơi mới, người chơi cũ hay hội viên VIP đều có cơ hội được hưởng ưu đãi đặc biệt từ nhà cái.
Giao dịch linh hoạt, tốc độ
Thương hiệu RGBET luôn chú tâm đến hệ thống giao dịch. Nhà cái cung cấp dịch vụ nạp rút nhanh chóng với đa dạng phương thức như thẻ cào, ví điện tử, ngân hàng điện tử, ngân hàng trực tiếp. Mọi hoạt động đều được bảo mật tuyệt đối bởi công nghệ mã hóa tiên tiến.
App cá độ RGBET
App cá độ RGBET là một ứng dụng cho phép người chơi đăng nhập RG nhanh chóng, đồng thời các thao tác đăng ký RG trên app cũng được tối ưu và trở nên đơn giản hơn. Tham gia cá cược RG bằng app cá độ, người chơi sẽ có 1 trải nghiệm cá cược tuyệt vời và thú vị.
RGBET Có Chứng Nhận Cá Cược Quốc Tế
Nhà cái RGBET hoạt động hợp pháp dưới sự cấp phép của hai tổ chức thế giới là PAGCOR và MGA, tính minh bạch và công bằng luôn được giám sát gắt gao bởi BIV. Khi tham gia cược tại đây, người chơi sẽ được đảm bảo quyền và lợi ích hợp pháp của mình.
Việc sở hữu các chứng nhận quốc tế còn cho thấy nguồn tài chính ổn định, dồi dào của RGBET. Điều này cho thấy việc một nhà cái được công nhận bởi các cơ quan quốc tế không phải là một chuyện dễ.
Theo quy định nhà cái RGBET, chỉ người chơi từ đủ 18 tuổi trở lên mới có thể tham gia cá cược tại RGBET
MGA (Malta Gaming Authority)
Tổ chức MGA đảm bảo tính vẹn toàn và ổn định của các trò chơi. Có các chính sách bảo vệ nguồn tài chính và quyền lợi của người chơi. Chứng nhận một nhà cái hoạt động có đầy đủ pháp lý, tuân thủ nghiêm chỉnh luật cờ bạc.
Chứng nhận Quần đảo Virgin Vương quốc Anh (BIV)
Tổ chứng chứng nhận nhà cái có đầy đủ tài chính để hoạt động kinh doanh cá cược. Với nguồn ngân sách dồi dào, ổn định nhà cái bảo đảm tính thanh khoản cho người chơi, mọi quyền lợi sẽ không bị xâm phạm.
Giấy Phép PAGCOR
Tổ chức cấp giấy phép cho nhà cái hoạt động đạt chuẩn theo tiêu chuẩn quốc tế. Cho phép nhà cái tổ chức cá cược một cách hợp pháp, không bị rào cản. Có chính sách ngăn chặn mọi trò chơi có dấu hiệu lừa đảo, duy trì sự minh bạch, công bằng.
Nhà Cái RGBET Phát Triển Công Nghệ
Nhà cái RGBET hỗ trợ trên nhiều thiết bị : IOS, Android, APP, WEB, Html5
RG và Trách Nhiệm Xã Hội
RGBET RichGame không đơn thuần là một trang cá cược giải trí mà nhà cái còn thể hiện rõ tính trách nhiệm xã hội của mình. Đơn vị luôn mong muốn người chơi tham gia cá cược phải có trách nhiệm với bản thân, gia đình và cả xã hội. Mọi hoạt động diễn ra tại RGBET trang chủ nói riêng hay bất kỳ trang web khác, người chơi phải thật sự bình tĩnh và lý trí, đừng để bản thân rơi vào “cạm bẫy của cờ bạc”.
RGBET RichGame với chính sách nghiêm cấm mọi hành vi xâm phạm thông tin cá nhân và gian lận nhằm tạo ra một môi trường cá cược công bằng, lành mạnh. Nhà cái khuyến cáo mọi cá nhân chưa đủ 18 tuổi không nên đăng ký RG và tham gia vào bất kỳ hoạt động cá cược nào.
Официальная покупка диплома вуза с упрощенной программой обучения
RGBET Trang Chủ Và Câu Chuyện Thương Hiệu
Ra đời vào năm 2010 tại Đài Loan, RGBET nhanh chóng trở thành một trang cá cược chất lượng hàng đầu khu vực Châu Á. Nhà cái được cấp phép hoạt động hợp pháp bởi công ty giải trí trực tuyến hợp pháp được ủy quyền và giám sát theo giấy phép Malta của Châu Âu – MGA. Và chịu sự giám sát chặt chẽ của tổ chức PAGCOR và BIV.
RGBET trang chủ cung cấp cho người chơi đa dạng các thể loại cược đặc sắc như: thể thao, đá gà, xổ số, nổ hũ, casino trực tuyến. Dịch vụ CSKH luôn hoạt động 24/7. Với chứng chỉ công nghệ GEOTRUST, nhà cái đảm bảo an toàn cho mọi giao dịch của khách hàng. APP RG thiết kế tối ưu giải quyết mọi vấn đề của người dùng IOS và Android.
Là một nhà cái đến từ đất nước công nghệ, nhà cái luôn không ngừng xây dựng và nâng cấp hệ thống game và dịch vụ hoàn hảo. Mọi giao dịch nạp rút được tự động hoá cho phép người chơi hoàn tất giao dịch chỉ với 2 phút vô cùng nhanh chóng
RGBET Lớn Nhất Uy Tín Nhất – Giá Trị Cốt Lõi
Nhà Cái RG Và Mục Tiêu Thương Hiệu
Giá trị cốt lõi mà RGBET mong muốn hướng đến đó chính là không ngừng hoàn thiện để đem đến một hệ thống chất lượng, công bằng và an toàn. Nâng cao sự hài lòng của người chơi, đẩy mạnh hoạt động chống gian lận và lừa đảo. RG luôn cung cấp hệ thống kèo nhà cái đặc sắc, cùng các sự kiện – giải đấu hàng đầu và tỷ lệ cược cạnh tranh đáp ứng mọi nhu cầu khách hàng.
Thương hiệu cá cược RGBET cam kết đem lại cho người chơi môi trường cá cược công bằng, văn minh và lành mạnh. Đây là nguồn động lực to lớn giúp nhà cái thực tế hóa các hoạt động của mình.
RGBET Có Tầm Nhìn Và Sứ Mệnh
Đổi mới và sáng tạo là yếu tố cốt lõi giúp đạt được mục tiêu dưới sự chuyển mình mạnh mẽ của công nghệ. Tầm nhìn và sứ mệnh của RGBET là luôn tìm tòi những điều mới lạ, đột phá mạnh mẽ, vượt khỏi giới hạn bản thân, đương đầu với thử thách để đem đến cho khách hàng sản phẩm hoàn thiện nhất.
Chúng tôi luôn sẵn sàng tiếp thu ý kiến và nâng cao bản thân mỗi ngày để tạo ra sân chơi bổ ích, uy tín và chuyên nghiệp cho người chơi. Để có thể trở thành nhà cái phù hợp với mọi khách hàng.
Khái Niệm Giá Trị Cốt Lõi Nhà Cái RGBET
Giá trị cốt lõi của nhà cái RG luôn gắn kết chặt chẽ với nhau giữa 5 khái niệm: Chính trực, chuyên nghiệp, an toàn, đổi mới, công nghệ.
Chính Trực
Mọi quy luật, cách thức của trò chơi đều được nhà cái cung cấp công khai, minh bạch và chi tiết. Mỗi tựa game hoạt động đều phải chịu sự giám sát kỹ lưỡng bởi các cơ quan tổ chức có tiếng về sự an toàn và minh bạch của nó.
Chuyên Nghiệp
Các hoạt động tại RGBET trang chủ luôn đề cao sự chuyên nghiệp lên hàng đầu. Từ giao diện đến chất lượng sản phẩm luôn được trau chuốt tỉ mỉ từng chi tiết. Thế giới giải trí được xây dựng theo văn hóa Châu Á, phù hợp với đại đa số thị phần khách Việt.
An Toàn
RG lớn nhất uy tín nhất luôn ưu tiên sử dụng công nghệ mã hóa hiện đại nhất để đảm bảo an toàn, riêng tư cho toàn bộ thông tin của người chơi. Đơn vị cam kết nói không với hành vi gian lận và mua bán, trao đổi thông tin cá nhân bất hợp pháp.
Đổi Mới
Nhà cái luôn theo dõi và bắt kịp xu hướng thời đại, liên tục bổ sung các sản phẩm mới, phương thức cá cược mới và các ưu đãi độc lạ, mang đến những trải nghiệm thú vị cho người chơi.
Công Nghệ
RGBET trang chủ tập trung xây dựng một giao diện game sắc nét, sống động cùng tốc độ tải nhanh chóng. Ứng dụng RGBET giải nén ít dung lượng phù hợp với mọi hệ điều hành và cấu hình, tăng khả năng sử dụng của khách hàng.
RGBET Khẳng Định Giá Trị Thương Hiệu
Hoạt động hợp pháp với đầy đủ giấy phép, chứng chỉ an toàn đạt tiêu chuẩn quốc tế
Hệ thống game đa màu sắc, đáp ứng được mọi nhu cầu người chơi
Chính sách bảo mật RG hiện đại và đảm bảo an toàn cho người chơi cá cược
Bắt tay hợp tác với nhiều đơn vị phát hành game uy tín, chất lượng thế giới
Giao dịch nạp rút RG cấp tốc, nhanh gọn, bảo mật an toàn
Kèo nhà cái đa dạng với bảng tỷ lệ kèo cao, hấp dẫn
Dịch Vụ RGBET Casino Online
Dịch vụ khách hàng
Đội ngũ CSKH RGBET luôn hoạt động thường trực 24/7. Nhân viên được đào tạo chuyên sâu luôn giải đáp tất cả các khó khăn của người chơi về các vấn đề tài khoản, khuyến mãi, giao dịch một cách nhanh chóng và chuẩn xác. Hạn chế tối đa làm ảnh hưởng đến quá trình trải nghiệm của khách hàng.
Đa dạng trò chơi
Với sự nhạy bén trong cập nhật xu thế, nhà cái RGBET đã dành nhiều thời gian phân tích nhu cầu khách hàng, đem đến một kho tàng game chất lượng với đa dạng thể loại từ RG casino online, thể thao, nổ hũ, game bài, đá gà, xổ số.
Khuyến mãi hấp dẫn
RGBET trang chủ liên tục cập nhật và thay đổi các sự kiện ưu đãi đầy hấp dẫn và độc đáo. Mọi thành viên bất kể là người chơi mới, người chơi cũ hay hội viên VIP đều có cơ hội được hưởng ưu đãi đặc biệt từ nhà cái.
Giao dịch linh hoạt, tốc độ
Thương hiệu RGBET luôn chú tâm đến hệ thống giao dịch. Nhà cái cung cấp dịch vụ nạp rút nhanh chóng với đa dạng phương thức như thẻ cào, ví điện tử, ngân hàng điện tử, ngân hàng trực tiếp. Mọi hoạt động đều được bảo mật tuyệt đối bởi công nghệ mã hóa tiên tiến.
App cá độ RGBET
App cá độ RGBET là một ứng dụng cho phép người chơi đăng nhập RG nhanh chóng, đồng thời các thao tác đăng ký RG trên app cũng được tối ưu và trở nên đơn giản hơn. Tham gia cá cược RG bằng app cá độ, người chơi sẽ có 1 trải nghiệm cá cược tuyệt vời và thú vị.
RGBET Có Chứng Nhận Cá Cược Quốc Tế
Nhà cái RGBET hoạt động hợp pháp dưới sự cấp phép của hai tổ chức thế giới là PAGCOR và MGA, tính minh bạch và công bằng luôn được giám sát gắt gao bởi BIV. Khi tham gia cược tại đây, người chơi sẽ được đảm bảo quyền và lợi ích hợp pháp của mình.
Việc sở hữu các chứng nhận quốc tế còn cho thấy nguồn tài chính ổn định, dồi dào của RGBET. Điều này cho thấy việc một nhà cái được công nhận bởi các cơ quan quốc tế không phải là một chuyện dễ.
Theo quy định nhà cái RGBET, chỉ người chơi từ đủ 18 tuổi trở lên mới có thể tham gia cá cược tại RGBET
MGA (Malta Gaming Authority)
Tổ chức MGA đảm bảo tính vẹn toàn và ổn định của các trò chơi. Có các chính sách bảo vệ nguồn tài chính và quyền lợi của người chơi. Chứng nhận một nhà cái hoạt động có đầy đủ pháp lý, tuân thủ nghiêm chỉnh luật cờ bạc.
Chứng nhận Quần đảo Virgin Vương quốc Anh (BIV)
Tổ chứng chứng nhận nhà cái có đầy đủ tài chính để hoạt động kinh doanh cá cược. Với nguồn ngân sách dồi dào, ổn định nhà cái bảo đảm tính thanh khoản cho người chơi, mọi quyền lợi sẽ không bị xâm phạm.
Giấy Phép PAGCOR
Tổ chức cấp giấy phép cho nhà cái hoạt động đạt chuẩn theo tiêu chuẩn quốc tế. Cho phép nhà cái tổ chức cá cược một cách hợp pháp, không bị rào cản. Có chính sách ngăn chặn mọi trò chơi có dấu hiệu lừa đảo, duy trì sự minh bạch, công bằng.
Nhà Cái RGBET Phát Triển Công Nghệ
Nhà cái RGBET hỗ trợ trên nhiều thiết bị : IOS, Android, APP, WEB, Html5
RG và Trách Nhiệm Xã Hội
RGBET RichGame không đơn thuần là một trang cá cược giải trí mà nhà cái còn thể hiện rõ tính trách nhiệm xã hội của mình. Đơn vị luôn mong muốn người chơi tham gia cá cược phải có trách nhiệm với bản thân, gia đình và cả xã hội. Mọi hoạt động diễn ra tại RGBET trang chủ nói riêng hay bất kỳ trang web khác, người chơi phải thật sự bình tĩnh và lý trí, đừng để bản thân rơi vào “cạm bẫy của cờ bạc”.
RGBET RichGame với chính sách nghiêm cấm mọi hành vi xâm phạm thông tin cá nhân và gian lận nhằm tạo ra một môi trường cá cược công bằng, lành mạnh. Nhà cái khuyến cáo mọi cá nhân chưa đủ 18 tuổi không nên đăng ký RG và tham gia vào bất kỳ hoạt động cá cược nào.
вывод из запоя цены сочи вывод из запоя цены сочи .
Официальное получение диплома техникума с упрощенным обучением в Москве
investicos.com/uncategorized/kupit-diplom-389359nnwy
Ремонт Дома Алматы – ТОО “Ваш-Ремонт” помжет Вам от идеи до реализации. Надежно, качественно и в срок. Мы предлагаем полный спектр услуг: от дизайна интерьера до отделочных работ любой сложности. Доверьте свой ремонт опытным специалистам и получите идеальный результат.
Приобретение диплома ПТУ с сокращенной программой обучения в Москве
купить диплом в ухте prema-diploms.ru .
Если вы искали где отремонтировать сломаную технику, обратите внимание – выездной ремонт бытовой техники в екатеринбурге
Полезные советы по безопасной покупке диплома о высшем образовании
turservisnews.ru/page/2
купить диплом в пензе server-diploms.ru .
Легальная покупка диплома о среднем образовании в Москве и регионах
Как получить диплом техникума официально и без лишних проблем
Всё, что нужно знать о покупке аттестата о среднем образовании
купить диплом в анжеро-судженске man-diploms.ru .
Как официально приобрести аттестат 11 класса с минимальными затратами времени
вывод из запоя цены сочи вывод из запоя цены сочи .
Реально ли приобрести диплом стоматолога? Основные шаги
the-trifecta-network.mn.co/posts/70000415
Удивительно, но купить диплом кандидата наук оказалось не так сложно
купить диплом физрука landik-diploms.ru .
Легальная покупка диплома ПТУ с сокращенной программой обучения
Стоимость дипломов высшего и среднего образования и процесс их получения
Приобретение школьного аттестата с официальным упрощенным обучением в Москве
aloha4d
капельница от запоя нижний новгород капельница от запоя нижний новгород .
вывод запой нижний https://snyatie-zapoya-na-domu15.ru .
капельница от запоя цена snyatie-zapoya-na-domu16.ru .
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
erudio.global/blog/index.php?entryid=37659
Как оказалось, купить диплом кандидата наук не так уж и сложно
gokong88
купить диплом в владикавказе orik-diploms.ru .
RGBET – Hướng Dẫn Truy Cập Nhà Cái RGBet Chính Thức Mới Nhất 2024
Cảnh Báo Về Các Trang Web Giả Mạo RGBET.INFO
Kính gửi quý khách hàng và người dùng thân mến,
Chúng tôi, đại diện chính thức của co], muốn thông báo về một số trang web giả mạo, đặc biệt là rgbet.info, đang mạo danh RGBet nhằm đánh lừa người dùng. Chúng tôi khẳng định rằng rgbet.info không có bất kỳ liên kết nào với RGBet chính thức, và việc truy cập vào các trang này có thể gây nguy cơ cho thông tin cá nhân cũng như tài khoản của bạn.
Việc giả mạo thương hiệu RGBet đã ảnh hưởng không nhỏ đến uy tín của chúng tôi và tiềm ẩn nguy cơ cho khách hàng. Những trang web này thường sẽ yêu cầu người dùng cung cấp thông tin nhạy cảm như số tài khoản ngân hàng, mật khẩu, hoặc các thông tin cá nhân khác, dễ dẫn đến mất mát tài sản hoặc dữ liệu cá nhân.
Cách Nhận Biết Liên Kết Chính Thức Của RGBet
Để đảm bảo sự an toàn tuyệt đối khi tham gia RGBet, khách hàng nên xác nhận rằng mình chỉ đang truy cập trang web RGBet thông qua liên kết chính thức tại co]. Đây là kênh duy nhất mà RGBet cung cấp để đảm bảo tính bảo mật, an toàn cho người dùng và tránh những rủi ro không đáng có. RGBet không bao giờ chuyển hướng người dùng đến trang web bên thứ ba như da88 hoặc các trang tương tự, và chúng tôi khuyến cáo bạn không nên tin tưởng những trang này.
Hướng Dẫn Và Hỗ Trợ Chính Thức Từ RGBet
RGBet luôn cố gắng hỗ trợ tốt nhất cho khách hàng thông qua các kênh liên lạc chính thức. Mọi thắc mắc, yêu cầu hỗ trợ hoặc vấn đề gặp phải khi truy cập có thể được giải đáp bởi đội ngũ hỗ trợ của chúng tôi. Vui lòng chỉ liên hệ thông qua các phương thức chính thức tại co] để đảm bảo thông tin được bảo mật.
Kính mong quý khách hàng luôn cảnh giác và lựa chọn RGBet một cách an toàn và thông minh để có trải nghiệm tuyệt vời nhất.
Trân trọng,
Đại Diện RGBet
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
w98804oc.beget.tech/2024/10/15/diplom-za-razumnye-dengi-i-minimalnoe-vremya.html
Легальная покупка школьного аттестата с упрощенной программой обучения
etoprosto.ru/ru/forum/?category=5&action=topic
ค่าย SA Gaming เป็น ค่าย เกม ไพ่บาคาร่า ออนไลน์ ที่ได้รับการยอมรับอย่างกว้างขวาง ใน ระดับสากล ว่าเป็น เจ้าตลาด ในการให้บริการ เกม คาสิโนออนไลน์ โดยเฉพาะในด้าน เกมไพ่ บาคาร่า ซึ่งเป็น เกม ที่ นักเล่น สนใจเล่นกัน อย่างแพร่หลาย ใน คาสิโนทั่วไป และ เว็บไซต์ ด้วย ลักษณะการเล่น ที่ สะดวก การเลือกเดิมพัน เพียง ฝั่ง ฝั่งผู้เล่น หรือ เจ้ามือ และ โอกาสชนะ ที่ ค่อนข้างสูง ทำให้ บาคาร่า ได้รับ ความนิยม อย่างมากใน ช่วงหลายปีนี้ โดยเฉพาะใน บ้านเรา
หนึ่งในวิธีการเล่น ยอดนิยมที่ SA Gaming เสนอ คือ Speed Baccarat ซึ่ง ให้โอกาสผู้เล่นที่ ต้องการ การตัดสินใจเร็ว และ การคิดไว สามารถ เดิมพันได้อย่างรวดเร็ว นอกจากนี้ยังมีโหมด ไม่มีค่าคอมมิชชั่น ซึ่งเป็น แบบ ที่ ไม่มีค่าคอมมิชชั่นเพิ่ม เมื่อชนะ การเดิมพัน ฝั่งเจ้ามือ ทำให้ โหมดนี้ ได้รับ ความนิยมมาก จาก ผู้เล่น ที่มองหา ความคุ้มค่า ในการ เสี่ยงโชค
เกมไพ่บาคาร่า ของ SA Gaming ยัง ได้รับการพัฒนา ให้มี กราฟฟิค ร่วมกับ เสียง ที่ เรียลไทม์ สร้างบรรยากาศ ที่ น่าตื่นเต้น เหมือนกับอยู่ใน คาสิโนจริง พร้อมกับ ฟังก์ชัน ที่ทำให้ นักเล่น สามารถเลือก วิธีแทง ที่ มีให้เลือกมากมาย ไม่ว่าจะเป็น การเดิมพัน ตามกลยุทธ์ ของตนเอง หรือการ พึ่งกลยุทธ์ ให้ชนะ นอกจากนี้ยังมี ดีลเลอร์จริง ที่ คอยดำเนินเกม ในแต่ละ โต๊ะ ทำให้ เกม มี ความน่าตื่นเต้น มากยิ่งขึ้น
ด้วย วิธี ใน การเสี่ยงโชค และ ความง่าย ในการ ใช้บริการ SA Gaming ได้ สร้างสรรค์ เกมไพ่ ที่ ตอบโจทย์ ทุก ชนิด ของผู้เล่น ตั้งแต่ นักเล่นมือใหม่ ไปจนถึง นักเดิมพัน มืออาชีพ
Как правильно купить диплом колледжа и пту в России, подводные камни
Официальная покупка диплома ПТУ с упрощенной программой обучения
hoki1881
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
rgbet
RGBET là nhà cái hàng đầu trong lĩnh vực cá cược trực tuyến, đem đến cho người chơi tại Việt Nam trải nghiệm giải trí đẳng cấp với nhiều lựa chọn hấp dẫn. RGBET không chỉ cung cấp các môn thể thao phổ biến như bóng đá, bóng rổ, hay quần vợt mà còn mở rộng với các trò chơi sòng bạc, xổ số và đặc biệt là cá cược eSports.
Lưu Ý Quan Trọng về Trang RGBET
Hiện nay, một số trang web giả mạo RGBET nhằm mục đích lừa đảo, gây rủi ro cho người chơi. Đặc biệt, trang rgbet.info không có liên kết chính thức với RGBET. Để bảo vệ thông tin cá nhân, khách hàng nên truy cập trang chính thức của RGBET tại rgbet.co và tránh các nguồn không uy tín.
Lợi Ích Khi Tham Gia RGBET
RGBET cung cấp rất nhiều chương trình khuyến mãi hấp dẫn dành cho người chơi, đặc biệt trong tháng 10 với chương trình “Mỗi Ngày Đăng Nhập, Nhận Ngay Quà Hot”. Ngoài ra, RGBET hỗ trợ nhiều tính năng cá cược thể thao trực tiếp với tỷ lệ cược hấp dẫn, giúp người chơi tận hưởng trọn vẹn từng trận đấu.
Đa Dạng Lựa Chọn Cá Cược và Trò Chơi Sòng Bạc
Sòng bạc trực tuyến: Bao gồm các trò chơi phổ biến như Baccarat, Roulette, và Blackjack.
Thể thao ảo và eSports: Người chơi có thể đặt cược các giải đấu lớn và thỏa sức với trò chơi thể thao ảo.
Trò chơi máy đánh bạc: Với hàng loạt trò chơi máy đánh bạc chủ đề như “Kho Báu Aztec” hay “Aladdin & Cây Đèn Thần,” RGBET đáp ứng nhu cầu giải trí đa dạng của người chơi.
Bảo Mật và Pháp Lý
RGBET là một trong số ít các nhà cái được cấp phép bởi cơ quan quản lý uy tín, đảm bảo tiêu chuẩn bảo mật và minh bạch.
Tham gia RGBET ngay để khám phá thế giới cá cược trực tuyến chuyên nghiệp và bảo đảm!
Можно ли быстро купить диплом старого образца и в чем подвох?
prema-diploms.ru
capecitabine drug – buy naprosyn generic buy danocrine without prescription
Аттестат школы купить официально с упрощенным обучением в Москве
investicos.com/uncategorized/kupit-diplom-702736ebeq
купить диплом о среднем образовании в астрахани prema-diploms.ru .
Как получить диплом техникума с упрощенным обучением в Москве официально
hoki1881
gokong88
RGBET – Hướng Dẫn Truy Cập Nhà Cái RGBet Chính Thức Mới Nhất 2024
Cảnh Báo Về Các Trang Web Giả Mạo RGBET.INFO
Kính gửi quý khách hàng và người dùng thân mến,
Chúng tôi, đại diện chính thức của [rgbet.co], muốn thông báo về một số trang web giả mạo, đặc biệt là rgbet.info, đang mạo danh RGBet nhằm đánh lừa người dùng. Chúng tôi khẳng định rằng rgbet.info không có bất kỳ liên kết nào với RGBet chính thức, và việc truy cập vào các trang này có thể gây nguy cơ cho thông tin cá nhân cũng như tài khoản của bạn.
Việc giả mạo thương hiệu RGBet đã ảnh hưởng không nhỏ đến uy tín của chúng tôi và tiềm ẩn nguy cơ cho khách hàng. Những trang web này thường sẽ yêu cầu người dùng cung cấp thông tin nhạy cảm như số tài khoản ngân hàng, mật khẩu, hoặc các thông tin cá nhân khác, dễ dẫn đến mất mát tài sản hoặc dữ liệu cá nhân.
Cách Nhận Biết Liên Kết Chính Thức Của RGBet
Để đảm bảo sự an toàn tuyệt đối khi tham gia RGBet, khách hàng nên xác nhận rằng mình chỉ đang truy cập trang web RGBet thông qua liên kết chính thức tại [rgbet.co]. Đây là kênh duy nhất mà RGBet cung cấp để đảm bảo tính bảo mật, an toàn cho người dùng và tránh những rủi ro không đáng có. RGBet không bao giờ chuyển hướng người dùng đến trang web bên thứ ba như da88 hoặc các trang tương tự, và chúng tôi khuyến cáo bạn không nên tin tưởng những trang này.
Hướng Dẫn Và Hỗ Trợ Chính Thức Từ RGBet
RGBet luôn cố gắng hỗ trợ tốt nhất cho khách hàng thông qua các kênh liên lạc chính thức. Mọi thắc mắc, yêu cầu hỗ trợ hoặc vấn đề gặp phải khi truy cập có thể được giải đáp bởi đội ngũ hỗ trợ của chúng tôi. Vui lòng chỉ liên hệ thông qua các phương thức chính thức tại [rgbet.co] để đảm bảo thông tin được bảo mật.
Kính mong quý khách hàng luôn cảnh giác và lựa chọn RGBet một cách an toàn và thông minh để có trải nghiệm tuyệt vời nhất.
Trân trọng,
Đại Diện RGBet
aloha4d
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
graph.org/Kupit-diplom-za-3-dnya-EHto-realno-10-14
Купить диплом ВУЗа России
kyc-diplom.com/diplom-articles/kupit-diplom-vuza-rossii.html
истинный запой http://vyvod-iz-zapoya-v-sankt-peterburge15.ru .
где купить диплом в оренбурге russa-diploms.ru .
вывод из запоя цены санкт-петербург https://www.azithromycinum.ru .
RGBET – Hướng Dẫn Truy Cập Nhà Cái RGBet Chính Thức Mới Nhất 2024
Cảnh Báo Về Các Trang Web Giả Mạo RGBET.INFO
Kính gửi quý khách hàng và người dùng thân mến,
Chúng tôi, đại diện chính thức của co], muốn thông báo về một số trang web giả mạo, đặc biệt là rgbet.info, đang mạo danh RGBet nhằm đánh lừa người dùng. Chúng tôi khẳng định rằng rgbet.info không có bất kỳ liên kết nào với RGBet chính thức, và việc truy cập vào các trang này có thể gây nguy cơ cho thông tin cá nhân cũng như tài khoản của bạn.
Việc giả mạo thương hiệu RGBet đã ảnh hưởng không nhỏ đến uy tín của chúng tôi và tiềm ẩn nguy cơ cho khách hàng. Những trang web này thường sẽ yêu cầu người dùng cung cấp thông tin nhạy cảm như số tài khoản ngân hàng, mật khẩu, hoặc các thông tin cá nhân khác, dễ dẫn đến mất mát tài sản hoặc dữ liệu cá nhân.
Cách Nhận Biết Liên Kết Chính Thức Của RGBet
Để đảm bảo sự an toàn tuyệt đối khi tham gia RGBet, khách hàng nên xác nhận rằng mình chỉ đang truy cập trang web RGBet thông qua liên kết chính thức tại co]. Đây là kênh duy nhất mà RGBet cung cấp để đảm bảo tính bảo mật, an toàn cho người dùng và tránh những rủi ro không đáng có. RGBet không bao giờ chuyển hướng người dùng đến trang web bên thứ ba như da88 hoặc các trang tương tự, và chúng tôi khuyến cáo bạn không nên tin tưởng những trang này.
Hướng Dẫn Và Hỗ Trợ Chính Thức Từ RGBet
RGBet luôn cố gắng hỗ trợ tốt nhất cho khách hàng thông qua các kênh liên lạc chính thức. Mọi thắc mắc, yêu cầu hỗ trợ hoặc vấn đề gặp phải khi truy cập có thể được giải đáp bởi đội ngũ hỗ trợ của chúng tôi. Vui lòng chỉ liên hệ thông qua các phương thức chính thức tại co] để đảm bảo thông tin được bảo mật.
Kính mong quý khách hàng luôn cảnh giác và lựa chọn RGBet một cách an toàn và thông minh để có trải nghiệm tuyệt vời nhất.
Trân trọng,
Đại Diện RGBet
Стоимость дипломов высшего и среднего образования и как избежать подделок
Профессиональный сервисный центр по ремонту Apple iPhone в Москве.
Мы предлагаем: сервисный центр iphone москва
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
где можно купить диплом в спб arusak-diploms.ru .
купить диплом парикмахера цена server-diploms.ru .
вывод из запоя на дому санкт-петербург вывод из запоя на дому санкт-петербург .
вывод из запоя в санкт-петербурге вывод из запоя в санкт-петербурге .
Рекомендации по безопасной покупке диплома о высшем образовании
вывод из запоя капельница [url=vyvod-iz-zapoya-v-sankt-peterburge16.ru]вывод из запоя капельница [/url] .
Процесс получения диплома стоматолога: реально ли это сделать быстро?
khvoynaya.getbb.ru/viewtopic.php?f=39&t=7475
Как получить диплом о среднем образовании в Москве и других городах
ทดลองเล่นสล็อต
ทดลองเล่นสล็อต PG: สัมผัสประสบการณ์เกมสล็อตออนไลน์แบบใหม่
ก่อนที่คุณจะเริ่มเล่นเกมสล็อตออนไลน์ สิ่งสำคัญคือการทำความรู้จักกับการทดลองเล่นเสียก่อน เกมสล็อต ทดลองเล่นสล็อต นั้นได้รับแรงบันดาลใจจากเครื่องสล็อตแบบดั้งเดิม โดยเฉพาะอย่างยิ่ง Triple Gold Slot ซึ่งเคยเป็นที่นิยมอย่างมากในคาสิโนต่างประเทศ ในเกมสล็อต ทดลองเล่นสล็อต PG ผู้เล่นจะได้สัมผัสกับรูปแบบของเกมที่มีความเรียบง่ายและคลาสสิก มาพร้อมกับรีล (Reel) จำนวน 5 แถวและเพย์ไลน์ (Payline) หรือรูปแบบการชนะรางวัลที่มากถึง 15 รูปแบบ ทำให้มีโอกาสชนะได้หลากหลายมากยิ่งขึ้น
สัญลักษณ์ต่าง ๆ ในเกมนี้สร้างความรู้สึกถึงบรรยากาศของสล็อตดั้งเดิม โดยมีสัญลักษณ์ที่เป็นที่รู้จักเช่น รูปเชอร์รี่ ตัวเลข 7 และเพชร ซึ่งนอกจากจะทำให้เกมมีความน่าสนใจแล้วยังเพิ่มโอกาสในการทำกำไรอีกด้วย
ความสะดวกสบายของเกมสล็อต PG
ทดลองเล่นสล็อต PG นั้นไม่เพียงแค่มีรูปแบบการเล่นที่เข้าใจง่าย แต่ยังมีความสะดวกสบายอย่างยิ่ง ไม่ว่าคุณจะใช้คอมพิวเตอร์หรือโทรศัพท์มือถือรุ่นใด เพียงแค่เชื่อมต่ออินเทอร์เน็ต คุณก็สามารถเข้าร่วมสนุกได้ทันที ทดลองเล่นสล็อต PG ยังถูกออกแบบมาให้รองรับอุปกรณ์หลากหลายประเภท เพื่อมอบประสบการณ์การเล่นที่ราบรื่นไม่ติดขัดแก่ผู้เล่นทุกคน
การเลือกธีมและรูปแบบเกม
ที่สำคัญ ทดลองเล่นสล็อต PG ยังมีหลากหลายธีมให้เลือกเล่น ไม่ว่าจะเป็นธีมที่น่าตื่นเต้น น่ารัก หรือธีมที่มีความสมจริง ทำให้ผู้เล่นสามารถสนุกสนานไปกับรูปแบบต่าง ๆ ตามความชอบ
ด้วยคุณสมบัติทั้งหมดนี้ ทดลองเล่นสล็อต PG ได้กลายเป็นตัวเลือกที่นิยมในหมู่ผู้เล่นเกมออนไลน์ที่กำลังมองหาความท้าทายใหม่ ๆ และการชนะที่ง่ายขึ้น หากคุณกำลังมองหาประสบการณ์ใหม่ ๆ การทดลองเล่นเกมสล็อตเป็นทางเลือกที่คุณไม่ควรพลาด!
Покупка диплома о среднем полном образовании: как избежать мошенничества?
купить диплом техникума в санкт петербурге man-diploms.ru .
купить диплом о среднем образование цена купить диплом о среднем образование цена .
Как правильно купить диплом колледжа и пту в России, подводные камни
ลองเล่นสล็อต พีจี: สัมผัสประสบการณ์เกมหมุนวงล้อออนไลน์แบบทันสมัย
ก่อนเริ่มเล่นสล๊อตออนไลน์ สิ่งสำคัญคือการทดลองกับการทดลองเล่นเสียล่วงหน้า เกม ลองเล่นสล็อตนั้นถูกสร้างสรรค์จากจากสล็อตแมชชีนแบบดั้งเดิม โดยเฉพาะเจาะจงมากๆ สล็อต Triple Gold ที่เคยเป็นที่รู้จักอย่างกว้างขวางในบ่อนการพนันต่างประเทศ ในเกม ทดลองเล่นสล๊อต PG ผู้เล่นจะได้เข้าถึงโครงสร้างของเกมการเล่นที่มีความไม่ซับซ้อนและแบบดั้งเดิม มาพร้อมกับวงล้อ (Reel) ที่มีจำนวนห้าแถวและช่องจ่ายเงิน (เพย์ไลน์) หรือแนวทางการชนะที่มากถึง 15 ลักษณะ ทำให้มีช่องทางชนะได้เพิ่มขึ้นมากขึ้นไป
รูปภาพต่าง ๆ ในเกมนี้เพิ่มความรู้สึกถึงอารมณ์ร่วมของสล็อตแบบดั้งเดิม โดยมีไอคอนที่คุ้นเคยเช่น ผลเชอร์รี่ เลข 7 และเพชร ที่จะทำให้เกมสล็อตน่าดึงดูดแล้วยังสร้างโอกาสในการทำกำไรเพิ่มเติม
ความง่ายดายของเกม PG
ทดลองเล่นเกม พีจี ในส่วนนี้ไม่ใช่แค่มีวิธีการการเล่นที่เข้าใจง่าย แต่ยังมีความสะดวกอย่างยิ่ง ไม่ว่าคุณจะใช้งานเครื่องคอมพิวเตอร์หรือโทรศัพท์มือถือรุ่นใด แค่เชื่อมต่ออินเทอร์เน็ต คุณก็สามารถเข้าสู่เกมได้ทันที ลองเล่น PG ยังถูกทำมาให้เหมาะสมกับเครื่องมือหลากหลายประเภท เพื่อมอบประสบการณ์การเล่นที่ไม่สะดุดไม่ชะงักแก่ลูกค้าทุกราย
การคัดสรรธีมและสไตล์เกม
ที่สำคัญ ทดลองเล่นสล็อต PG ยังมีหลากหลายธีมให้สนุกกับ โดยไม่จำกัดธีมที่น่าตื่นเต้น น่าเอ็นดู หรือธีมที่มีความใกล้เคียงจริง ทำให้ผู้เล่นได้สนุกสนานไปกับแนวทางใหม่ ๆตามความพอใจ
จากฟีเจอร์หลากหลายนี้ ลองเล่นเกมสล็อต พีจี ได้กลายเป็นตัวเลือกที่นิยมในกลุ่มนักเล่นเกมสมัยใหม่ที่กำลังต้องการประสบการณ์ใหม่ ๆและการคว้ารางวัลที่เป็นไปได้มากขึ้น หากคุณกำลังแสวงหาความแปลกใหม่ การทดลองเล่นเกมสล็อตเป็นทางเลือกที่คุณไม่ควรละเลย!
Как быстро и легально купить аттестат 11 класса в Москве
Парадокс, но купить диплом кандидата наук оказалось не так и сложно
цветочный магазин бизнес план с расчетами цветочный магазин бизнес план с расчетами .
бизнес флористика бизнес флористика .
бизнес план цветочного магазина кратко cvetov-ray.ru .
отдел маркетинга на аутсорсе http://www.marketing99.ru .
снятие ломки недорого снятие ломки недорого .
Возможно ли купить диплом стоматолога, и как это происходит
Как официально купить диплом вуза с упрощенным обучением в Москве
veniaminv.flybb.ru/posting.php?mode=post&f=1
купить юридический диплом купить юридический диплом .
возможно ли купить диплом возможно ли купить диплом .
Как быстро и легально купить аттестат 11 класса в Москве
Всё, что нужно знать о покупке аттестата о среднем образовании
Полезная информация как купить диплом о высшем образовании без рисков
Официальная покупка школьного аттестата с упрощенным обучением в Москве
Быстрая схема покупки диплома старого образца: что важно знать?
Узнайте стоимость диплома высшего и среднего образования и процесс получения
снять ломку наркомана снять ломку наркомана .
Аттестат школы купить официально с упрощенным обучением в Москве
вывод из запоя воронеж вывод из запоя воронеж .
снятие наркологической ломки на дому снятие наркологической ломки на дому .
снятие ломок снятие ломок .
снятие наркологической ломки снятие наркологической ломки .
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Удивительно, но купить диплом кандидата наук оказалось не так сложно
купить диплом о среднем образовании в тюмени [url=https://server-diploms.ru/]server-diploms.ru[/url] .
Сервисный центр предлагает ремонт texet x4 tm-5082 в петербурге ремонт texet x4 tm-5082 цены
Быстрая покупка диплома старого образца: возможные риски
forum.amzgame.com/thread/detail?id=316397
Реально ли приобрести диплом стоматолога? Основные этапы
Как получить диплом стоматолога быстро и официально
вывод из запоя в стационаре нижний новгород вывод из запоя в стационаре нижний новгород .
вывод из запоя в стационаре https://vyvod-iz-zapoya-v-stacionare16.ru/ .
за выводом из запоя в стационаре за выводом из запоя в стационаре .
вывод из запоя в стационаре http://www.vyvod-iz-zapoya-v-stacionare14.ru .
Официальная покупка диплома вуза с сокращенной программой в Москве
диплом мама купить man-diploms.ru .
Полезные советы по безопасной покупке диплома о высшем образовании
purchase prometrium generic – cheap clomiphene pills buy fertomid generic
Как получить диплом о среднем образовании в Москве и других городах
купить аттестат за 11 класс отзывы купить аттестат за 11 класс отзывы .
купить дубликат диплома купить дубликат диплома .
лечение запоя в стационаре http://vyvod-iz-zapoya-v-stacionare-voronezh16.ru .
Рекомендации по безопасной покупке диплома о высшем образовании
sky-metaverse.com/read-blog/22506
Можно ли быстро купить диплом старого образца и в чем подвох?
team-clo.mn.co/posts/69549512
лечению наркозависимости в стационаре лечению наркозависимости в стационаре .
вывод из запоя в стационаре Самары вывод из запоя в стационаре Самары .
вывод из запоя в стационаре Самары вывод из запоя в стационаре Самары .
анонимный вывод из запоя в стационаре https://vyvod-iz-zapoya-v-stacionare-samara17.ru/ .
купить диплом московская область russa-diploms.ru .
Вопросы и ответы: можно ли быстро купить диплом старого образца?
weekevents.ru/kupit-diplom-universiteta-nedorogo
Аттестат школы купить официально с упрощенным обучением в Москве
Полезные советы по покупке диплома о высшем образовании без риска
капельница на дому от запоя капельница на дому от запоя .
Пошаговая инструкция по официальной покупке диплома о высшем образовании
купить готовый диплом о среднем специальном образовании prema-diploms.ru .
fosamax ca – purchase nolvadex pills buy generic provera
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Сервисный центр предлагает качественый ремонт телефонов doogee ремонт телефона doogee на дому
Сколько стоит диплом высшего и среднего образования и как это происходит?
купить диплом луганск купить диплом луганск .
неотложная наркологическая помощь в москве неотложная наркологическая помощь в москве .
состав капельницы для вывода из запоя https://kapelnica-ot-zapoya-kolomna16.ru/ .
как вызвать наркологическую скорую помощь в москве как вызвать наркологическую скорую помощь в москве .
капельницу коломна от запоя капельницу коломна от запоя .
неотложная наркологическая помощь в москве неотложная наркологическая помощь в москве .
Вопросы и ответы: можно ли быстро купить диплом старого образца?
Пошаговая инструкция по официальной покупке диплома о высшем образовании
Можно ли купить аттестат о среднем образовании, основные моменты и вопросы
Приобретение диплома ПТУ с сокращенной программой обучения в Москве
купить диплом хирурга купить диплом хирурга .
купить готовый диплом новосибирск server-diploms.ru .
Всё, что нужно знать о покупке аттестата о среднем образовании
a90275db.beget.tech/2024/10/20/bystryy-start-s-diplomom.html
Как правильно купить диплом колледжа и пту в России, подводные камни
Как приобрести аттестат о среднем образовании в Москве и других городах
купить диплом о среднем специальном образовании недорого man-diploms.ru .
выведение из запоя химки выведение из запоя химки .
наркологическая скорая наркологическая скорая .
вывод из запоя на дому химки круглосуточно вывод из запоя на дому химки круглосуточно .
вывод из запоя химки стационар вывод из запоя химки стационар .
наркологическая скорая наркологическая скорая .
подделка диплома о высшем образовании подделка диплома о высшем образовании .
купить красный диплом о среднем образовании купить красный диплом о среднем образовании .
Быстрое обучение и получение диплома магистра – возможно ли это?
什麼是娛樂城？
娛樂城是一個讓玩家能夠透過網絡進行賭場遊戲的平台，與真實賭場相似，玩家可在此參與真錢遊戲。如果在娛樂城的遊戲中獲勝，便能賺取真金！賭博公社作為一個專業的娛樂城推薦平台，致力於為玩家提供真實、客觀的娛樂城評價資訊，幫助玩家選擇值得信賴的線上娛樂城。
娛樂城的專業術語
返水：返水是娛樂城回饋給玩家的金額，計算方式為「有效投注額 × 返水百分比」，是娛樂城用以激勵玩家的一種方式。
派彩：派彩指的是玩家在娛樂城遊戲中獲得的利潤。當玩家贏得遊戲後，娛樂城會將相應的獎金支付給玩家。
出金：出金是指玩家將娛樂城帳戶中的獲利轉出至個人帳戶的過程，這是玩家贏取獎金後將金額提取到自己帳戶的重要一步。
娛樂城儲值與出金流程
選擇線上娛樂城。
選擇存取款選項。
進入個人帳戶頁面進行存款操作。
輸入儲值或出金的金額。
完成操作，順利進行娛樂城的儲值或出金。
最受歡迎的娛樂城遊戲
在賭博公社中，從玩家的評價中篩選出一些廣受歡迎的娛樂城遊戲。第一名的是真人百家樂，隨後是電子老虎機。以下為部分熱門遊戲推薦：
DG百家樂 – ⭐️⭐️⭐️⭐️⭐️ (4826條評論)
DB百家樂 – ⭐️⭐️⭐️⭐️⭐️ (3554條評論)
RG百家樂 – ⭐️⭐️⭐️⭐️★ (4687條評論)
歐博真人 – ⭐️⭐️⭐️⭐️★ (3512條評論)
SA真人 – ⭐️⭐️⭐️⭐️★ (2415條評論)
關於賭博公社
賭博公社秉持著專業知識，致力於屏蔽各類網路上的娛樂城詐騙信息，並成為台灣首屈一指的娛樂城推薦指南。賭博公社提供最新的娛樂城排名，查證線上論壇如Dcard、Ptt及Facebook的娛樂城評價，為玩家提供真實可靠的資訊，幫助他們找到最安全、最值得信賴的賭博網站。
為何信任賭博公社？
賭博公社堅持客觀、公正的原則，提供娛樂城的真實評價與最新資訊。在當今資訊爆炸的網路時代，賭博公社作為玩家的嚮導，幫助他們避免陷入不實宣傳的陷阱，讓玩家能夠享受安全、合法的線上娛樂城遊戲體驗。
線上娛樂城常見問題
台灣線上娛樂城推薦哪些？ 可以參考娛樂城排行來選擇。
娛樂城在台灣是否合法？ 必須參考當地法規，以保證遊戲的合法性。
線上娛樂城是否安全？ 賭博公社僅推薦持有合法執照並保證出金的娛樂城，保護玩家的權益。
在線上娛樂城贏錢需要繳稅嗎？ 這取決於當地的稅務規定，玩家應查詢相關政策。
哪裡可以玩免費的線上娛樂城？ 部分娛樂城提供免費試玩，玩家可以無需儲值體驗遊戲。
賭博公社致力於為玩家提供全方位的娛樂城資訊，是玩家尋找可靠娛樂城的理想指南。
Полезная информация как купить диплом о высшем образовании без рисков
usa.life/read-blog/76188
สล็อตเว็บตรง
สล็อตไม่ผ่านเอเย่นต์คือระบบการเล่นบนอินเทอร์เน็ตที่ให้นักเล่นเกมเข้าถึงสล็อตแมชชีนได้โดยตรงจากหน้าเว็บ โดยไม่ต้องผ่านผู้แทนหรือตัวกลางใดๆ ข้อดีของสล็อตเว็บตรงคือการป้องกันเพิ่มขึ้น เนื่องจากนักเดิมพันไม่ต้องกังวลเรื่องโอกาสเสี่ยงจากการใช้บริการผ่านตัวกลาง อีกทั้งยังมีการจ่ายเงินรางวัลที่มากกว่าและข้อเสนอพิเศษมากมาย เนื่องจากไม่มีค่านายหน้าจากผู้แทน ทำให้นักเล่นเข้าถึงเกมสปินได้อย่างสะดวกและรวดเร็ว พร้อมรับประสบการณ์การเล่นเกมที่มีคุณภาพและไม่สะดุด
การเล่น สล็อตตรง ไม่เหมือนกับ สล็อตแบบดั้งเดิมอย่างไร?
เว็บสล็อตตรงเป็นทางเลือกที่ไม่มีการผ่านผู้แทน ทำให้นักเล่นสามารถเข้าถึงได้โดยตรง เกมสล็อตและเงินรางวัลได้โดยตรงจากผู้ดำเนินการ ลดโอกาสเสี่ยงในการเสียเปรียบหรือเสียค่าใช้จ่ายสูง นอกจากนี้ เว็บสล็อตโดยตรงยังมีความหลากหลายของเกมสปินให้เลือกสรรมากกว่าในสล็อตดั้งเดิม เนื่องจากสล็อตเว็บตรงมักจะได้รับการอัปเดตและเพิ่มเกมใหม่ๆอย่างไม่หยุดยั้ง อัตราการให้รางวัล (RTP) ของสล็อตเว็บตรงมักจะมากกว่าสล็อตดั้งเดิม เนื่องจากไม่มีค่าธรรมเนียมพิเศษ ทำให้ผู้เล่นได้รับกำไรที่คุ้มค่า อีกทั้งยัง โปรโมชั่นและรางวัลที่หลากหลายกว่า โดยเว็บสล็อตตรงมักมีข้อเสนอเพิ่มเติมและโปรแกรมคะแนนที่ให้ความคุ้มค่ามากขึ้น
โปรโมชันและโบนัสในสล็อตตรงที่น่าสนใจ
สล็อตเว็บตรงมักมีโปรโมชันและโบนัสที่ดีมากสำหรับนักเดิมพัน เริ่มตั้งแต่โบนัสสมาชิกใหม่สำหรับผู้เล่นใหม่ เงินเพิ่มในการฝาก เครดิตเล่นฟรี รวมถึงการสะสมคะแนนที่สามารถแลกแต้มหรือข้อเสนอพิเศษได้ ทำให้ผู้เล่นได้รับผลตอบแทนและสิทธิประโยชน์มากมาย การมีโปรโมชั่นที่น่าดึงดูดช่วยให้ผู้เล่นสามารถเพิ่มโอกาสรับรางวัลและลดค่าใช้จ่ายในการเล่น นอกจากนี้ยังมีโปรโมชันเสริมเช่นคืนเงินบางส่วนจากยอดเสียและของแจกตามเทศกาลต่างๆอีกด้วย
สรุปแล้ว เว็บสล็อตโดยตรงเป็นตัวเลือกที่ดีสำหรับผู้ที่ต้องการ ความสะดวกและความปลอดภัยในการเล่นเกม มีอัตราการจ่ายที่มากกว่า ข้อเสนอที่หลากหลาย และความสนุกในการเล่นที่ดีโดยไม่มีการผ่านเอเย่นต์
Официальная покупка диплома вуза с упрощенной программой обучения
duduslot login
duduslot adalah link resmi yang memberikan persentase kemenangan yang sangat tinggi. Dengan bermain di duduslot, akan memberikan saran game gacor berupa RTP agar kemungkinan dapat jakcpot lebih besar.
купить диплом электромеханика купить диплом электромеханика .
выведение из запоя на дому люберцы выведение из запоя на дому люберцы .
капельница от запоя люберцы капельница от запоя люберцы .
вывод из запоя люберцы москва вывод из запоя люберцы москва .
нарколог на дом вывод из запоя москва нарколог на дом вывод из запоя москва .
вывод из запоя на дому москва цены вывод из запоя на дому москва цены .
สล็อตเว็บตรง
เว็บสล็อตโดยตรงคือระบบการเล่นเกมออนไลน์ที่ให้ผู้เล่นเข้าถึงเกมสล็อตได้โดยตรงจากเว็บ โดยไม่ต้องใช้บริการจากตัวแทนหรือตัวกลางใดๆ ข้อดีของเว็บสล็อตตรงคือการรักษาความปลอดภัยเพิ่มขึ้น เนื่องจากนักเล่นไม่ต้องกังวลใจเรื่องโอกาสเสี่ยงจากการใช้บริการผ่านเอเย่นต์ อีกทั้งยังมีการมอบเงินรางวัลที่มากกว่าและข้อเสนอพิเศษมากมาย เนื่องจากไม่มีค่าธรรมเนียมจากตัวแทน ทำให้นักเล่นเข้าถึงเกมแมชชีนได้อย่างง่ายและรวดเร็ว พร้อมรับการเล่นที่น่าพอใจและไม่ติดขัด
การเล่น สล็อตเว็บตรง แตกต่างจาก สล็อตทั่วไปอย่างไร?
สล็อตไม่ผ่านเอเย่นต์เป็นทางเลือกที่ไม่มีการผ่านเอเย่นต์ ทำให้นักเล่นสามารถเข้าถึงเกมได้ทันที เกมสล็อตและเงินรางวัลได้โดยตรงจากเจ้าของเว็บ ลดโอกาสเสี่ยงในการถูกหลอกหรือเสียค่าธรรมเนียมสูง นอกจากนี้ เว็บสล็อตโดยตรงยังมีความหลากหลายของเกมสปินให้เลือกเล่นมากกว่าในสล็อตแบบเดิม เนื่องจากสล็อตเว็บตรงมักจะอัปเดตบ่อยและเพิ่มเกมใหม่อย่างไม่หยุดยั้ง อัตราการให้รางวัล (เรทการจ่าย) ของเว็บสล็อตมักจะมากกว่าสล็อตแบบดั้งเดิม เนื่องจากไม่มีค่าธรรมเนียมพิเศษ ทำให้ผู้เล่นได้รับรางวัลที่มีมูลค่ามากกว่า ทั้งยัง โปรโมชั่นและโปรโมชั่นพิเศษที่มากกว่า โดยสล็อตเว็บตรงมักมีข้อเสนอพิเศษและโปรแกรมสะสมแต้มที่ให้ความคุ้มค่ามากขึ้น
ข้อเสนอพิเศษและโบนัสในเว็บสล็อตตรงที่น่าสนใจ
สล็อตเว็บตรงมักมีโปรโมชั่นและโปรโมชั่นพิเศษที่น่าสนใจสำหรับผู้เล่น เริ่มตั้งแต่โบนัสต้อนรับสำหรับผู้เล่นใหม่ โบนัสเติมเงิน เครดิตฟรี รวมถึงการสะสมคะแนนที่สามารถแลกเป็นเงินหรือข้อเสนอพิเศษได้ ทำให้นักเดิมพันได้รับผลตอบแทนและข้อดีมากมาย การมีโปรโมชั่นที่น่าสนใจช่วยให้ผู้เล่นสามารถเพิ่มโอกาสรับรางวัลและลดเงินลงทุนในการเล่น นอกจากนี้ยังมีโปรโมชั่นพิเศษเช่นเงินคืนบางส่วนและรางวัลพิเศษตามเทศกาลต่างๆอีกด้วย
สรุปว่า สล็อตตรงเป็นตัวเลือกที่ดีสำหรับผู้เล่นที่อยากได้ ความสะดวกและการป้องกันในการเล่น มีการจ่ายเงินที่สูงกว่าปกติ โปรโมชั่นมากมาย และความสนุกในการเล่นที่ยอดเยี่ยมโดยไม่มีการใช้ตัวแทน
Сервисный центр предлагает ремонт casio exilim ex-z350 ремонт casio exilim ex-z350
Легальная покупка диплома о среднем образовании в Москве и регионах
Быстрая схема покупки диплома старого образца: что важно знать?
Приобретение школьного аттестата с официальным упрощенным обучением в Москве
situs kantorbola
Парадокс, но купить диплом кандидата наук оказалось не так и сложно
Как правильно приобрести диплом колледжа или ПТУ в России, важные моменты
вывод из запоя круглосуточно москва вывод из запоя круглосуточно москва .
круглосуточный вывод из запоя в балашихе круглосуточный вывод из запоя в балашихе .
капельница от запоя в балашихе капельница от запоя в балашихе .
выведение из запоя в балашихе https://vyvod-iz-zapoya-v-stacionare-balashiha13.ru/ .
купить диплом о среднем пермь prema-diploms.ru .
вывод из запоя цены москва вывод из запоя цены москва .
rtp slot gacor
Hercules99: Daftar 8 Gim Uji Coba PGS Anti Penipuan Dapat Dipercaya di Indonesia
PGS telah menjadi kesukaan untuk para penggemar slot di negeri ini, menawarkan berbagai permainan slot yang seru dengan sensasi dan kesenangan non-stop. Di saat popularitasnya semakin tinggi, timbul kekhawatiran tentang adanya kecurangan atau ketidakadilan dalam judi online. Namun demikian, Permainan PG Slot dapat mengatasi menghadapi permasalahan tersebut dengan memperkenalkan slot yang aman dari kecurangan yang aman dan terpercaya.
Dengan teknologi keamanan terbaru dan fitur inovatif, Permainan PG Slot memastikan bahwa setiap game adil dan aman untuk semua pemain. Berikut daftar 8 game demo PG bebas dari penipuan yang populer dan dapat dipercaya di Indonesia:
1. Demo Fortune Mouse PG Slot
Mouse of Fortune adalah game slot yang penuh daya tarik dengan visual yang indah serta tema menarik. Selain tampilan visualnya, game ini memiliki enkripsi kuat agar melindungi semua data pemain. Seluruh putaran bebas dari campur tangan luar, agar pemain merasa nyaman bermain.
2. Demo Dragon Hatch PG Slot
Dragon Hatch memasukkan player ke dunia mistis yang dipenuhi kemegahan dan kekuatan ajaib. Namun keunggulan permainan ini terdapat pada fitur keamanannya. Dilengkapi proteksi anti-kecurangan, slot ini memastikan setiap kemenangan tanpa gangguan tanpa adanya manipulasi dari luar.
3. Demo Journey Wealth PGS
Game Journey to the Wealth mengundang pemain ke petualangan mencari kekayaan tanpa batas. Memiliki bonus melimpah dan RTP yang tinggi, permainan ini memberikan kenikmatan bertambah sekaligus jaminan keadilan pada setiap putarannya. User mendapatkan sensasi kenikmatan bermain tanpa kekhawatiran akan kecurangan.
4. Demo Surga Bikini PG Slot
Aplikasi ini membuat pemain terjun ke suasana pulau yang indah yang elok serta penuh keceriaan. Di balik keindahan tropisnya, Game Bikini dilengkapi dengan protokol keamanan yang kuat, dan menjadikannya salah satu game PG Slot bebas manipulasi yang terjamin. User bisa menikmati permainan tanpa khawatir akan adanya kecurangan.
5. Demo Medusa II: The Quest of Perseus Slot PG
Pada permainan Medusa II, pengguna terjun dalam kisah epik menghadapi makhluk legendaris. Game ini dilengkapi dengan keamanan mutakhir yang memastikan setiap putaran aman. Karenanya, player dapat fokus untuk menang tanpa ada campur tangan eksternal.
6. Versi Demo Bombs Away Pocket Games Slot
Dengan tema peperangan yang sengit, Slot Bom memacu adrenalin player. Dalam ketegangan permainan, fokus pada keamanan utama. Sistem pengamanan PG Soft memastikan keamanan transaksi dan hasil, memberikan rasa aman kepada player di jalan menuju kemenangan.
7. Demo Pertarungan Banteng PGS
Bull Fight mengajak pemain ke arena yang mendebarkan. Di dalam game ini, PG Soft memastikan keadilan dalam setiap giliran. Pemain bisa menikmati sensasi permainan yang adil dan aman tanpa rasa khawatir akan manipulasi.
8. Percobaan Muay Thai PG Slot
Game Muay Thai Champion mengusung tema bertarung yang seru, memasukkan pengguna dalam duel di atas ring. Gim ini tidak hanya seru karena tema, dan juga keamanannya. Setiap giliran diawasi ketat, menjamin pengalaman bermain yang bebas dari gangguan dan kecurangan.
Kelebihan Memilih Demo Slot PG Soft Ber-RTP Tinggi
Demo game PG Soft anti-kecurangan mempunyai RTP yang lebih tinggi dari standar rata-rata. Dengan begitu, peluang pemain meningkat untuk mendapatkan profit dari investasi. Memilih game slot dari PG Soft bukan hanya soal hiburan, juga memberi peluang keuntungan besar.
Dengan daftar game di atas, pemain dapat menikmati pengalaman bermain slot yang adil, aman, dan menyenangkan. Dengan teknologi mutakhir dari PG Slot membuat setiap permainan aman tanpa gangguan, memberikan kepercayaan penuh bagi para pemainnya.
demo pg slot
Jelajahi dunia fantasi dan keamanan di mesin slot PG Soft
Slot online telah menjadi salah satu hiburan paling populer di kalangan para gamer. Dengan banyaknya pilihan yang tersedia, PG Soft Slots menonjol sebagai salah satu penyedia terkemuka yang tidak hanya menawarkan pengalaman bermain game yang mengasyikkan, tetapi juga mengutamakan keamanan dan keadilan dalam setiap permainan. Pada artikel ini kita akan melihat beberapa versi demo menarik dari mesin slot PG Soft dan menekankan pentingnya memiliki sistem keamanan.
1. Versi demo Luke Dragon
Dragon Hatch mengajak pemain untuk terjun ke dunia fantasi yang kaya akan kekuatan sihir dan mistik. Namun, fokus utama dari game ini adalah sistem keamanan yang kompleks. Dengan teknologi canggih yang melindungi setiap sesi permainan, pemain bisa menang tanpa khawatir akan gangguan.
2. Slot demo Perjalanan Menuju Kekayaan Hal
Seperti namanya, Journey to Wealth adalah perjalanan menuju kekayaan tanpa akhir. Game ini menawarkan fitur bonus yang menggiurkan dan RTP yang kompetitif. Kegembiraan dan keadilan adalah dua hal yang saling melengkapi di setiap putaran, memastikan bahwa setiap kemenangan diperoleh secara adil.
3. Versi demo slot Bikini Paradise Pg
Di balik keindahan dan pesona tropis Bikini Paradise terdapat protokol keamanan yang ketat. Game ini tidak hanya menawarkan gameplay yang seru namun juga memberikan ketenangan pikiran bagi para pemainnya. Berkat sistem yang terintegrasi, setiap transaksi dan hasil permainan dijamin terlindungi dari penipuan.
4. Slot demo Medusa II: Pencarian Perseus Hal
Medusa II: The Quest of Perseus menawarkan petualangan epik berlatar mitos kuno, mengirim pemain ke pertempuran melawan monster legendaris. Namun perhatian terhadap keselamatan tidak pernah dilupakan. Teknologi terbaru digunakan untuk menjaga integritas setiap putaran, memungkinkan pemain untuk fokus pada kemenangan tanpa gangguan.
5. Versi demo slot Bombs Away Pg
Mengusung tema perang dunia yang menegangkan, Bombs Away menjanjikan gameplay yang seru. Meski demikian, PG Soft tetap mengutamakan keselamatan. Sistem yang canggih memastikan setiap transaksi dan hasil permainan tersimpan sehingga memberikan kepercayaan diri pemain untuk terus berjuang meraih kemenangan.
6. Versi demo mesin slot Bull Fight Hal
Bull Fight mengajak pemain ke arena adu banteng yang seru. Di sini, keberanian dan keterampilan adalah kunci kemenangan. PG Soft menjamin keadilan dan keadilan di setiap putaran permainan, menciptakan pengalaman bermain yang sempurna.
7. Versi demo mesin slot Champion Pg Muay Thai
Menampilkan tema seni bela diri yang menarik, Juara Muay Thai melibatkan pemain dalam pertarungan intens di atas ring. Selain aksinya yang seru, PG Soft juga menekankan pentingnya keselamatan. Setiap putaran dipantau dan dijaga dengan cermat untuk memastikan gameplay tanpa gangguan eksternal.
Keuntungan memainkan soft slot versi demo dengan RTP PG tinggi
Salah satu keuntungan utama memainkan game demo PG Soft adalah RTP-nya yang tinggi, seringkali lebih tinggi dari rata-rata industri. Ini berarti bahwa pemain memiliki peluang lebih besar untuk menghasilkan keuntungan besar dari investasi mereka. Tak heran jika mesin slot PG Soft yang memadukan kesenangan bermain game dan keamanan terjamin menjadi pilihan favorit para gamer.
Di dunia yang terus berkembang ini, PG Soft tidak hanya berhasil menciptakan gameplay yang seru, tetapi juga aman dan adil. Dengan berbagai versi demo permainan yang menarik, pemain dapat menjelajahi keajaiban tanpa khawatir akan risiko yang tidak diinginkan.
Легальные способы покупки диплома о среднем полном образовании
Легальная покупка диплома ПТУ с сокращенной программой обучения
Узнайте, как безопасно купить диплом о высшем образовании
Парадокс, но купить диплом кандидата наук оказалось не так и сложно
whoah this weblog is fantastic i like reading your posts. Keep up the great work! You realize, lots of people are looking around for this info, you could help them greatly.
накрутка поведенческих факторов заказать
диплома orik-diploms.ru .
Процесс получения диплома стоматолога: реально ли это сделать быстро?
выведение из запоя на дому в подольске http://kapelnica-ot-zapoya-podolsk11.ru/ .
капельница от запоя подольск капельница от запоя подольск .
королев вывод из запоя королев вывод из запоя .
вывод из запоя с выездом королев vyvod-iz-zapoya-korolev12.ru .
капельница от запоя подольск капельница от запоя подольск .
สล็อตเว็บตรงคือระบบเกมผ่านเน็ตที่ให้ผู้เล่นเชื่อมต่อสล็อตแมชชีนได้โดยตรงจากเว็บไซต์ โดยไม่ต้องผ่านผู้แทนหรือตัวกลางใดๆ ข้อดีของเว็บสล็อตตรงคือการรักษาความปลอดภัยที่มากขึ้น เนื่องจากนักเล่นไม่ต้องกังวลใจเรื่องการเสี่ยงจากการใช้บริการผ่านตัวกลาง อีกทั้งยังมีการมอบเงินรางวัลที่เหนือกว่าและข้อเสนอพิเศษมากมาย เนื่องจากไม่มีค่าธรรมเนียมจากตัวแทน ทำให้นักเดิมพันเข้าถึงเกมสล็อตได้อย่างง่ายและว่องไว พร้อมรับประสบการณ์การเล่นที่มีคุณภาพและไม่สะดุด
การเล่น สล็อตเว็บตรง ต่างจาก สล็อตปกติอย่างไร?
เว็บสล็อตตรงเป็นตัวเลือกที่ดีที่ไม่มีการผ่านผู้แทน ทำให้นักเล่นสามารถเข้าถึงเกมได้ทันที เกมสล็อตและเงินรางวัลได้โดยตรงจากผู้ดำเนินการ ลดโอกาสเสี่ยงในการเสียเปรียบหรือถูกหักค่าใช้จ่ายสูง นอกจากนี้ สล็อตตรงยังมีหลายแบบของเกมให้เลือกเล่นมากกว่าในสล็อตดั้งเดิม เนื่องจากสล็อตเว็บตรงมักจะได้รับการอัปเดตและเพิ่มเกมหลากหลายอย่างไม่หยุดยั้ง อัตราการให้รางวัล (RTP) ของสล็อตเว็บตรงมักจะสูงกว่าสล็อตทั่วไป เนื่องจากไม่มีค่าใช้จ่ายเพิ่มเติม ทำให้นักเดิมพันได้รับรางวัลที่สูงขึ้น อีกทั้งยัง โปรโมชั่นและโบนัสที่มากกว่า โดยเว็บสล็อตตรงมักมีข้อเสนอเพิ่มเติมและโปรแกรมสะสมแต้มที่ให้ความคุ้มค่ามากขึ้น
ข้อเสนอพิเศษและโบนัสในเว็บสล็อตตรงที่น่าสนใจ
เว็บสล็อตโดยตรงมักมีโปรโมชันและโปรโมชั่นพิเศษที่น่าสนใจสำหรับนักเดิมพัน เริ่มตั้งแต่โบนัสสมาชิกใหม่สำหรับผู้ที่เพิ่งสมัคร โบนัสเงินฝากเพิ่ม โบนัสฟรี รวมถึงการสะสมคะแนนที่สามารถแลกแต้มหรือสิทธิประโยชน์ต่างๆได้ ทำให้นักเดิมพันได้รับความคุ้มค่าและประโยชน์มากมาย การมีข้อเสนอที่น่าสนใจช่วยให้นักเล่นเกมสามารถเพิ่มโอกาสในการชนะและประหยัดเงินในการเล่น นอกจากนี้ยังมีข้อเสนอพิเศษเช่นคืนเงินบางส่วนจากยอดเสียและของแจกตามวันสำคัญอีกด้วย
สรุปว่า สล็อตเว็บตรงเป็นตัวเลือกที่ดีสำหรับผู้เล่นที่อยากได้ ความสะดวกและการรักษาความปลอดภัยในการเล่นเกม มีอัตราการจ่ายที่สูงกว่า ข้อเสนอที่หลากหลาย และการเล่นเกมที่ยอดเยี่ยมโดยไม่มีการผ่านเอเย่นต์
Do you have any video of that? I’d like to find out some additional information.
заказать отзыв за деньги
Покупка диплома о среднем полном образовании: как избежать мошенничества?
ST666 trang chủ
ST666 Trang Chủ Chính Thức Hàng Đầu 2024
ST666 đã khẳng định vị thế của mình như một trong những cổng game trực tuyến chất lượng trong năm 2024. Với sự phát triển không ngừng và luôn nâng cao chất lượng dịch vụ, ST666 mang đến cho người dùng một trải nghiệm giải trí trực tuyến đa dạng và an toàn.
Tại sao ST666 lại được yêu thích?
Khuyến mãi ST666 hấp dẫn: ST666 luôn dẫn đầu xu hướng với nhiều sự kiện ưu đãi đặc sắc như tết trung thu, hướng về miền Trung, v.v. Gần đây nhất là khuyến mãi đặc biệt mừng sinh nhật 6 tuổi với những ưu đãi khủng sau:
Khuyến Mãi
Tiền Thưởng
Lì xì tân thủ 66K
66.000 VND
Freebet hàng tuần
166.000 VND
Thưởng nạp đầu 160%
3.666.000 VND
Livestream chất, Rinh Honda Civic
Ô tô Honda Civic
Hoàn trả thể thao & đá gà 10% mỗi ngày
6.666.000 VND
Ngoài ra, ST666 còn được yêu thích bởi:
Uy tín và minh bạch: ST666 hoạt động dưới sự cấp phép của chính phủ Campuchia và được giám sát bởi tổ chức uy tín PAGCOR.
Đa dạng trò chơi: Trang web cung cấp nhiều loại trò chơi cá cược hấp dẫn như cá cược thể thao, casino trực tuyến, xổ số, và slot game.
Giao dịch nhanh chóng: Hỗ trợ nhiều phương thức thanh toán tiện lợi, giúp người chơi thực hiện giao dịch nạp và rút tiền một cách nhanh chóng và an toàn.
Dịch vụ khách hàng chuyên nghiệp: Đội ngũ hỗ trợ khách hàng luôn sẵn sàng 24/7, đảm bảo giải đáp mọi thắc mắc của người chơi.
Khám phá kho game khổng lồ của ST666
ST666 tự hào mang đến một kho game cá cược trực tuyến đa dạng và phong phú:
Xổ số: Tham gia cá cược các loại xổ số phổ biến như xổ số Việt Nam, Keno, và xổ số Thái Lan với tỷ lệ thưởng cao và nhiều hình thức đặt cược.
Đá gà: Cá cược các trận đá gà trực tiếp từ Campuchia với hình ảnh sắc nét và âm thanh sống động.
Cá cược thể thao: Cung cấp các trận đấu từ các giải đấu lớn như Ngoại hạng Anh, La Liga, Serie A, Champions League và World Cup với tỷ lệ cược cạnh tranh.
Casino trực tuyến: Trải nghiệm các trò chơi casino trực tuyến như Baccarat, Blackjack, Roulette, và Poker với dealer chuyên nghiệp và hình ảnh sắc nét.
Slot game: Khám phá thế giới slot game với hàng ngàn chủ đề hấp dẫn và cơ hội nhận thưởng jackpot khủng.
Game bài: Tham gia các game bài dân gian như Tiến lên miền Nam, Phỏm, Mậu binh, và Liêng với nhiều bàn chơi và mức cược khác nhau.
Bắn cá: Tham gia trò chơi bắn cá với đồ họa đẹp mắt và âm thanh sống động.
E-sport: Cá cược các trận thi đấu Esport từ các giải đấu danh giá với tỷ lệ cược cập nhật liên tục.
Kết luận
ST666 cam kết mang đến cho người chơi những trải nghiệm giải trí tuyệt vời nhất với kho game đa dạng và chất lượng cao. Tham gia ngay hôm nay để khám phá thế giới giải trí bất tận và nhận nhiều ưu đãi hấp dẫn!
Как правильно приобрести диплом колледжа или ПТУ в России, важные моменты
vmestedeshevle.listbb.ru/viewtopic.php?f=10&t=13564
Купить диплом старого образца, можно ли это сделать по быстрой схеме?
купить диплом о высшем образовании с занесением в реестр в казани купить диплом о высшем образовании с занесением в реестр в казани .
Jelajahi dunia fantasi dan keamanan di mesin slot PG Soft
Slot online telah menjadi salah satu hiburan paling populer di kalangan para gamer. Dengan banyaknya pilihan yang tersedia, PG Soft Slots menonjol sebagai salah satu penyedia terkemuka yang tidak hanya menawarkan pengalaman bermain game yang mengasyikkan, tetapi juga mengutamakan keamanan dan keadilan dalam setiap permainan. Pada artikel ini kita akan melihat beberapa versi demo menarik dari mesin slot PG Soft dan menekankan pentingnya memiliki sistem keamanan.
1. Versi demo Luke Dragon
Dragon Hatch mengajak pemain untuk terjun ke dunia fantasi yang kaya akan kekuatan sihir dan mistik. Namun, fokus utama dari game ini adalah sistem keamanan yang kompleks. Dengan teknologi canggih yang melindungi setiap sesi permainan, pemain bisa menang tanpa khawatir akan gangguan.
2. Slot demo Perjalanan Menuju Kekayaan Hal
Seperti namanya, Journey to Wealth adalah perjalanan menuju kekayaan tanpa akhir. Game ini menawarkan fitur bonus yang menggiurkan dan RTP yang kompetitif. Kegembiraan dan keadilan adalah dua hal yang saling melengkapi di setiap putaran, memastikan bahwa setiap kemenangan diperoleh secara adil.
3. Versi demo slot Bikini Paradise Pg
Di balik keindahan dan pesona tropis Bikini Paradise terdapat protokol keamanan yang ketat. Game ini tidak hanya menawarkan gameplay yang seru namun juga memberikan ketenangan pikiran bagi para pemainnya. Berkat sistem yang terintegrasi, setiap transaksi dan hasil permainan dijamin terlindungi dari penipuan.
4. Slot demo Medusa II: Pencarian Perseus Hal
Medusa II: The Quest of Perseus menawarkan petualangan epik berlatar mitos kuno, mengirim pemain ke pertempuran melawan monster legendaris. Namun perhatian terhadap keselamatan tidak pernah dilupakan. Teknologi terbaru digunakan untuk menjaga integritas setiap putaran, memungkinkan pemain untuk fokus pada kemenangan tanpa gangguan.
5. Versi demo slot Bombs Away Pg
Mengusung tema perang dunia yang menegangkan, Bombs Away menjanjikan gameplay yang seru. Meski demikian, PG Soft tetap mengutamakan keselamatan. Sistem yang canggih memastikan setiap transaksi dan hasil permainan tersimpan sehingga memberikan kepercayaan diri pemain untuk terus berjuang meraih kemenangan.
6. Versi demo mesin slot Bull Fight Hal
Bull Fight mengajak pemain ke arena adu banteng yang seru. Di sini, keberanian dan keterampilan adalah kunci kemenangan. PG Soft menjamin keadilan dan keadilan di setiap putaran permainan, menciptakan pengalaman bermain yang sempurna.
7. Versi demo mesin slot Champion Pg Muay Thai
Menampilkan tema seni bela diri yang menarik, Juara Muay Thai melibatkan pemain dalam pertarungan intens di atas ring. Selain aksinya yang seru, PG Soft juga menekankan pentingnya keselamatan. Setiap putaran dipantau dan dijaga dengan cermat untuk memastikan gameplay tanpa gangguan eksternal.
Keuntungan memainkan soft slot versi demo dengan RTP PG tinggi
Salah satu keuntungan utama memainkan game demo PG Soft adalah RTP-nya yang tinggi, seringkali lebih tinggi dari rata-rata industri. Ini berarti bahwa pemain memiliki peluang lebih besar untuk menghasilkan keuntungan besar dari investasi mereka. Tak heran jika mesin slot PG Soft yang memadukan kesenangan bermain game dan keamanan terjamin menjadi pilihan favorit para gamer.
Di dunia yang terus berkembang ini, PG Soft tidak hanya berhasil menciptakan gameplay yang seru, tetapi juga aman dan adil. Dengan berbagai versi demo permainan yang menarik, pemain dapat menjelajahi keajaiban tanpa khawatir akan risiko yang tidak diinginkan.
Jelajahi dunia fantasi dan keamanan di mesin slot PG Soft
Slot online telah menjadi salah satu hiburan paling populer di kalangan para gamer. Dengan banyaknya pilihan yang tersedia, PG Soft Slots menonjol sebagai salah satu penyedia terkemuka yang tidak hanya menawarkan pengalaman bermain game yang mengasyikkan, tetapi juga mengutamakan keamanan dan keadilan dalam setiap permainan. Pada artikel ini kita akan melihat beberapa versi demo menarik dari mesin slot PG Soft dan menekankan pentingnya memiliki sistem keamanan.
1. Versi demo Luke Dragon
Dragon Hatch mengajak pemain untuk terjun ke dunia fantasi yang kaya akan kekuatan sihir dan mistik. Namun, fokus utama dari game ini adalah sistem keamanan yang kompleks. Dengan teknologi canggih yang melindungi setiap sesi permainan, pemain bisa menang tanpa khawatir akan gangguan.
2. Slot demo Perjalanan Menuju Kekayaan Hal
Seperti namanya, Journey to Wealth adalah perjalanan menuju kekayaan tanpa akhir. Game ini menawarkan fitur bonus yang menggiurkan dan RTP yang kompetitif. Kegembiraan dan keadilan adalah dua hal yang saling melengkapi di setiap putaran, memastikan bahwa setiap kemenangan diperoleh secara adil.
3. Versi demo slot Bikini Paradise Pg
Di balik keindahan dan pesona tropis Bikini Paradise terdapat protokol keamanan yang ketat. Game ini tidak hanya menawarkan gameplay yang seru namun juga memberikan ketenangan pikiran bagi para pemainnya. Berkat sistem yang terintegrasi, setiap transaksi dan hasil permainan dijamin terlindungi dari penipuan.
4. Slot demo Medusa II: Pencarian Perseus Hal
Medusa II: The Quest of Perseus menawarkan petualangan epik berlatar mitos kuno, mengirim pemain ke pertempuran melawan monster legendaris. Namun perhatian terhadap keselamatan tidak pernah dilupakan. Teknologi terbaru digunakan untuk menjaga integritas setiap putaran, memungkinkan pemain untuk fokus pada kemenangan tanpa gangguan.
5. Versi demo slot Bombs Away Pg
Mengusung tema perang dunia yang menegangkan, Bombs Away menjanjikan gameplay yang seru. Meski demikian, PG Soft tetap mengutamakan keselamatan. Sistem yang canggih memastikan setiap transaksi dan hasil permainan tersimpan sehingga memberikan kepercayaan diri pemain untuk terus berjuang meraih kemenangan.
6. Versi demo mesin slot Bull Fight Hal
Bull Fight mengajak pemain ke arena adu banteng yang seru. Di sini, keberanian dan keterampilan adalah kunci kemenangan. PG Soft menjamin keadilan dan keadilan di setiap putaran permainan, menciptakan pengalaman bermain yang sempurna.
7. Versi demo mesin slot Champion Pg Muay Thai
Menampilkan tema seni bela diri yang menarik, Juara Muay Thai melibatkan pemain dalam pertarungan intens di atas ring. Selain aksinya yang seru, PG Soft juga menekankan pentingnya keselamatan. Setiap putaran dipantau dan dijaga dengan cermat untuk memastikan gameplay tanpa gangguan eksternal.
Keuntungan memainkan soft slot versi demo dengan RTP PG tinggi
Salah satu keuntungan utama memainkan game demo PG Soft adalah RTP-nya yang tinggi, seringkali lebih tinggi dari rata-rata industri. Ini berarti bahwa pemain memiliki peluang lebih besar untuk menghasilkan keuntungan besar dari investasi mereka. Tak heran jika mesin slot PG Soft yang memadukan kesenangan bermain game dan keamanan terjamin menjadi pilihan favorit para gamer.
Di dunia yang terus berkembang ini, PG Soft tidak hanya berhasil menciptakan gameplay yang seru, tetapi juga aman dan adil. Dengan berbagai versi demo permainan yang menarik, pemain dapat menjelajahi keajaiban tanpa khawatir akan risiko yang tidak diinginkan.
купить диплом ру 2orik-diploms.ru .
купить диплом туризм 3russkiy-diploms.ru .
купить диплом врача стоматолога prem-diplom77.ru .
Аттестат школы купить официально с упрощенным обучением в Москве
купить диплом высшее екатеринбург servera-diplomy199.ru .
прерывание запоев http://vyvod-iz-zapoya-voronezh12.ru .
выведение из запоя королев выведение из запоя королев .
срочная помощь вывод из запоя королев https://www.vyvod-iz-zapoya-korolev13.ru .
прерывание запоев http://www.vyvod-iz-zapoya-voronezh11.ru .
прерывание запоев http://www.vyvod-iz-zapoya-voronezh13.ru .
Please let me know if you’re looking for a author for your weblog. You have some really great posts and I think I would be a good asset. If you ever want to take some of the load off, I’d really like to write some material for your blog in exchange for a link back to mine. Please blast me an email if interested. Regards!
накрутка пф в яндекс
Быстрая схема покупки диплома старого образца: что важно знать?
Всё, что нужно знать о покупке аттестата о среднем образовании без рисков
диплом кандидата наук нового образца купить prema365-diploms.ru .
Быстрая покупка диплома старого образца: возможные риски
Hey there! I know this is sort of off-topic but I had to ask. Does building a well-established website such as yours take a massive amount work? I am brand new to blogging but I do write in my diary everyday. I’d like to start a blog so I can share my personal experience and thoughts online. Please let me know if you have any recommendations or tips for new aspiring bloggers. Thankyou!
накрутка пф авито заказать
Тут можно преобрести противопожарный сейф купить огнестойкий сейф в москве
Amazing! Its really amazing piece of writing, I have got much clear idea on the topic of from this article.
накрутка пф яндекс быдлокодер
Всё о покупке аттестата о среднем образовании: полезные советы
buy generic aygestin – bimatoprost allergy spray yasmin buy online
Как не попасть впросак при покупке диплома колледжа или ПТУ в России
Можно ли купить аттестат о среднем образовании? Основные рекомендации
pg slot gacor
Hercule99: Daftar 8 buah Aplikasi Uji Coba PGS Tanpa Kecurangan Terpercaya di Tanah Air
PG Slot telah menjadi pilihan kesukaan bagi banyak pecinta slot di Nusantara, menawarkan aneka permainan slot yang menyenangkan dengan sensasi dan kesenangan tanpa batas. Seiring ketenaran yang semakin besar, ada juga kecemasan seputar penipuan atau gangguan dalam permainan judi online. Namun, PG Slot sudah sukses menghadapi permasalahan tersebut dengan memperkenalkan game slot tanpa manipulasi yang aman serta dapat dipercaya.
Dilengkapi fitur keamanan terkini dan fitur mutakhir, Game PG Slot memberikan jaminan bahwa setiap game aman dan terkontrol untuk seluruh pemain. Berikut daftar 8 game demo PG Slot tanpa manipulasi yang gacor dan dapat dipercaya di Tanah Air:
1. Demo Fortune Mouse PG Slot
Fortuna Mouse merupakan permainan slot yang menarik perhatian berbekal grafis cantik dengan tema lucu. Di luar desainnya, game ini didukung enkripsi canggih PG Soft yang mengamankan data pemain. Setiap putaran dijamin bebas dari manipulasi, agar permainan tetap nyaman.
2. Demo Slot Dragon Hatch
Dragon Hatch mengajak pemain ke dunia fantasi yang dipenuhi keistimewaan dan kekuatan mistis. Meski demikian, daya tarik utama game ini terdapat pada fitur keamanannya. Berbekal fitur anti-manipulasi, permainan ini mewujudkan keadilan dalam kemenangan tanpa gangguan bebas dari campur tangan luar.
3. Demo Journey Wealth PGS
Game Perjalanan Menuju Kekayaan memanggil user dalam perjalanan ke arah kekayaan tanpa akhir. Dengan bonus yang besar dan RTP yang tinggi, permainan ini menghadirkan kenikmatan bertambah serta kepastian keadilan pada setiap putarannya. User mendapatkan sensasi keseruan bermain tanpa perlu khawatir mengenai manipulasi.
4. Uji Coba Bikini Paradise Pocket Games Slot
Slot ini membuat pemain terjun ke suasana pulau tropis yang indah dan penuh sukacita. Di balik nuansa santainya, Game Bikini dilengkapi dengan protokol keamanan yang kuat, dan menjadikannya salah satu game PGS anti-rungkad yang diandalkan. User bisa bermain dengan tenang tanpa curang.
5. Demo Medusa II: Misi Perseus Pocket Games Slot
Pada permainan Medusa II, pemain dibawa pada kisah epik melawan makhluk mitos. Gim ini menggunakan teknologi keamanan terkini yang menjaga integritas setiap putaran. Karenanya, player dapat fokus untuk menang tanpa ada campur tangan eksternal.
6. Versi Demo Bombs Away Slot PG
Dengan tema perang yang intens, Bombs Away memicu semangat pemain. Di antara ketegangan bermain, fokus pada keamanan utama. Pengamanan PG Soft mengamankan semua transaksi dan hasil game, memberikan rasa aman bagi pemain saat mengejar kemenangan.
7. Versi Demo Pertarungan Banteng PG Slot
Adu Banteng memasukkan player dalam arena matador menantang. Dalam game ini, PG Soft menjaga integritas tiap putaran. Pemain dapat bermain dengan adil dan tanpa cemas tanpa takut akan kecurangan.
8. Demo Juara Muay Thai PG Slot
Slot Muay Thai Champion bertema seni bela diri menarik, mengundang player bertarung sengit di ring. Game ini tidak hanya memikat dari sisi tema, tapi juga dari sisi keamanan. Setiap giliran diawasi ketat, menghadirkan pengalaman bermain yang jujur dan lancar.
Keuntungan Bermain Demo Slot PG Soft dengan RTP Tinggi
Demo game PG Soft anti-kecurangan dikenal dengan RTP besar yang di atas standar industri. Dengan begitu, peluang pemain meningkat untuk meraih pengembalian dari investasi mereka. Bermain slot dari PG Soft bukan cuma hiburan, tetapi juga peluang keuntungan yang lebih tinggi.
Melalui list game yang tersedia di atas, pemain bisa menikmati slot dengan keadilan, keamanan, dan kesenangan. Teknologi modern di PG Slot membuat setiap permainan aman tanpa gangguan, memberikan kepercayaan penuh bagi para pemainnya.
цена вывода из запоя анонимно цена вывода из запоя анонимно .
выведение из запоя на дому в екатеринбурге выведение из запоя на дому в екатеринбурге .
вывод из запоя в челябинске http://www.vyvod-iz-zapoya-chelyabinsk12.ru .
помощь на дому вывод из запоя помощь на дому вывод из запоя .
вывод из запоя на дому екатеринбург круглосуточно вывод из запоя на дому екатеринбург круглосуточно .
Можно ли купить аттестат о среднем образовании? Основные рекомендации
Тут можно преобрести сейф под оружие цена пистолетные сейфы москва
Тут можно где купить сейф для дома сейфы домашние
Официальное получение диплома техникума с упрощенным обучением в Москве
Тут можно преобрести сейф противопожарный купить сейф огнеупорный купить
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Home decor Promo Codes https://skidki-i-kupony.ru/ .
instagram anonymous story viewer storyviewerfree.com .
вызов нарколога на дом екатеринбург вызов нарколога на дом екатеринбург .
электрокарнизы для штор купить электрокарнизы для штор купить .
нарколог на дом екатеринбург нарколог на дом екатеринбург .
Диплом вуза купить официально с упрощенным обучением в Москве
Официальная покупка диплома ПТУ с упрощенной программой обучения
Полезные советы по безопасной покупке диплома о высшем образовании
Процесс получения диплома стоматолога: реально ли это сделать быстро?
Купить диплом старого образца, можно ли это сделать по быстрой схеме?
Тут можно преобрести сейфы для оружия интернет магазин сейф для охотничьего ружья цена
Стоимость дипломов высшего и среднего образования и процесс их получения
сколько стоит диплом врача сколько стоит диплом врача .
Как оказалось, купить диплом кандидата наук не так уж и сложно
teseygroup.ru/question/ofitsialnyj-diplom-bez-lishnih-usilij-prosto-i-bystro/
купить диплом о высшем образовании в ставрополе many-diplom77.ru .
Как приобрести диплом техникума с минимальными рисками
insta stories insta stories .
заказать проект перепланировки квартиры в москве цена http://www.stoimost-soglasovaniya-pereplanirovki-kvartiry.ru .
искусственная кожа для обивки мебели искусственная кожа для обивки мебели .
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
Сколько стоит диплом высшего и среднего образования и как его получить?
hobbyland.moibb.ru/viewtopic.php?f=3&t=219
сервис для накрутки подписчиков в инстаграме сервис для накрутки подписчиков в инстаграме .
купить диплом конкурса prema365-diploms.ru .
Тут можно преобрести оружейный шкаф купить сейф охотничий
view insta stories anonymously http://storyinst.com .
Как приобрести аттестат о среднем образовании в Москве и других городах
Диплом вуза купить официально с упрощенным обучением в Москве
uzmanendustri.com/kupit-attestat-v-bryanske.html
Процесс получения диплома стоматолога: реально ли это сделать быстро?
Можно ли быстро купить диплом старого образца и в чем подвох?
Официальная покупка диплома ПТУ с упрощенной программой обучения
купить дипломы о высшем образовании в москве с занесением в реестр купить дипломы о высшем образовании в москве с занесением в реестр .
купить диплом лэти servera-diplomy199.ru .
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Как получить диплом техникума с упрощенным обучением в Москве официально
промокод Getcourse Pay [url=https://www.platezhnyj-modul-getkurs-promokod.ru]https://www.platezhnyj-modul-getkurs-promokod.ru[/url] .
сервис накрутки подписчиков тик ток сервис накрутки подписчиков тик ток .
Можно ли быстро купить диплом старого образца и в чем подвох?
продвижение сайтов продвижение сайтов .
продвижение сайтов в москве заказать продвижение сайтов в москве заказать .
продвижение сайтов москва продвижение сайтов москва .
недорогие франшизы http://www.franshizy17.ru/ .
Сколько стоит диплом высшего и среднего образования и как его получить?
Официальная покупка диплома вуза с сокращенной программой в Москве
poznanie.gtaserv.ru/memberlist.php
Где и как купить диплом о высшем образовании без лишних рисков
Парадокс, но купить диплом кандидата наук оказалось не так и сложно
Сколько стоит диплом высшего и среднего образования и как это происходит?
Легальная покупка диплома о среднем образовании в Москве и регионах
Тут можно преобрести огнестойкие сейфы сейф несгораемый
Тут можно преобрести сейф оружейный купить москва оружейные шкафы
Сервисный центр предлагает ремонт экшен камер panasonic рядом отремонтировать экшен камеры panasonic
Всё, что нужно знать о покупке аттестата о среднем образовании без рисков
Полезные советы по безопасной покупке диплома о высшем образовании
Приобретение школьного аттестата с официальным упрощенным обучением в Москве
анонимный. вывод. из. запоя. ростов. http://www.ideya.forums.party/viewtopic.php?id=653/ .
франшиза каталог франшиза каталог .
франшизу купить франшизу купить .
по франшизе по франшизе .
франшиза купить готовый бизнес недорого франшиза купить готовый бизнес недорого .
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Официальная покупка диплома вуза с упрощенной программой обучения
Вопросы и ответы: можно ли быстро купить диплом старого образца?
Покупка диплома о среднем полном образовании: как избежать мошенничества?
ulmo.ukrbb.net/index.php
Реально ли приобрести диплом стоматолога? Основные этапы
Можно ли быстро купить диплом старого образца и в чем подвох?
Тут можно преобрести огнестойкие сейфы цена огнеупорный сейф купить
Как получить диплом стоматолога быстро и официально
Тут можно преобрести сейф для оружия купить в москве оружейные сейфы интернет магазин
ST666 trang chủ
ST666 – Nhà Cái Uy Tín Hàng Đầu Việt Nam
ST666 là một trong những nhà cái uy tín số 1 tại Việt Nam, cung cấp đa dạng các trò chơi cá cược hấp dẫn như cá cược thể thao, casino, xổ số, đá gà, bắn cá, và nhiều trò chơi thú vị khác. Không chỉ vậy, ST666 còn mang đến các chương trình khuyến mãi hấp dẫn, giúp người chơi nhận được nhiều ưu đãi hấp dẫn khi tham gia.
Trò Chơi Cá Cược Tại ST666
ST666 cung cấp các trò chơi cá cược đa dạng, đáp ứng nhu cầu của mọi đối tượng người chơi. Các trò chơi nổi bật tại ST666 bao gồm:
Cá Cược Thể Thao: Các sự kiện thể thao hấp dẫn từ bóng đá, tennis đến các môn thể thao khác.
Casino: Trải nghiệm các trò chơi casino với chất lượng cao như blackjack, baccarat, roulette, và các trò chơi slot machines.
Đá Gà: Trận đấu đá gà gay cấn, nơi người chơi có thể tham gia cá cược và theo dõi những trận đấu kịch tính.
Xổ Số: Chơi xổ số và thử vận may để nhận những phần thưởng giá trị.
Bắn Cá: Trò chơi bắn cá với đồ họa sống động và hấp dẫn.
Esports: Tham gia cá cược vào các trận đấu thể thao điện tử hấp dẫn với các đội tuyển hàng đầu.
Khuyến Mãi Hấp Dẫn
ST666 luôn có các chương trình khuyến mãi hấp dẫn để tri ân người chơi, bao gồm:
Khuyến Mãi 100% Nạp Lần Đầu: Người chơi mới khi đăng ký tài khoản và nạp tiền lần đầu sẽ nhận được khuyến mãi nạp tiền lên tới 100%.
Bảo Hiểm Casino: ST666 cung cấp bảo hiểm cho các trò chơi casino, giúp người chơi giảm thiểu rủi ro khi tham gia.
Khuyến Mãi Thể Thao: Các chương trình khuyến mãi hấp dẫn dành riêng cho cá cược thể thao, giúp người chơi gia tăng cơ hội chiến thắng.
Đăng Ký và Đăng Nhập ST666
Để bắt đầu trải nghiệm các trò chơi và tham gia cá cược tại ST666, người chơi cần thực hiện các bước đơn giản sau:
Đăng Ký: Tạo tài khoản tại ST666 để nhận các ưu đãi và khuyến mãi hấp dẫn.
Đăng Nhập: Sau khi đăng ký thành công, người chơi có thể đăng nhập vào tài khoản để tham gia các trò chơi cá cược trực tuyến.
Nạp Tiền và Rút Tiền: ST666 hỗ trợ nhiều phương thức nạp và rút tiền linh hoạt, giúp người chơi giao dịch nhanh chóng và an toàn.
ST666 – Nơi Gửi Gắm Niềm Tin
ST666 không chỉ là nhà cái mà còn là nơi cung cấp môi trường cá cược công bằng và minh bạch. Người chơi luôn cảm thấy an tâm với các chính sách bảo mật chặt chẽ và dịch vụ hỗ trợ khách hàng 24/7. ST666 xứng đáng là điểm đến tin cậy cho những ai yêu thích cá cược trực tuyến.
Thông Tin Liên Hệ
Nếu bạn có bất kỳ câu hỏi hay thắc mắc nào, vui lòng liên hệ với ST666 qua các kênh hỗ trợ khách hàng. Chúng tôi luôn sẵn sàng giải đáp và hỗ trợ bạn.
CEO & Founder: Đặng Nhất Nam
Facebook ST666: Cập nhật những tin tức mới nhất và nhận các khuyến mãi hấp dẫn tại trang Facebook chính thức của ST666.
купить диплом медицинского вуза купить диплом медицинского вуза .
Официальная покупка диплома вуза с сокращенной программой в Москве
вывод из запоя на дому ростов http://chesskomi.borda.ru/?1-8-0-00003044-000-0-0-1730725479 .
вывод из запоя дешево ростов на дону https://vkontakte.forum.cool/viewtopic.php?id=19611/ .
нарколог на дом вывод из запоя ростов http://www.motik13.0pk.me/viewtopic.php?id=1993/ .
вывод. из. запоя. ростов. http://www.belbeer.borda.ru/?1-6-0-00000751-000-0-0-1730725764 .
вывод из запоя дешево ростов-на-дону http://www.odessaforum.0pk.me/viewtopic.php?id=10053/ .
Покупка школьного аттестата с упрощенной программой: что важно знать
Как официально купить диплом вуза с упрощенным обучением в Москве
Быстрое обучение и получение диплома магистра – возможно ли это?
продамус промокод http://prodamus-promokod1.ru/ .
Всё, что нужно знать о покупке аттестата о среднем образовании
Как получить диплом техникума официально и без лишних проблем
Купить диплом старого образца, можно ли это сделать по быстрой схеме?
lessigles.fr/kupit-attestat-ob-okonchanii-11-klassov-v-naberezhnih-chelnah.html
Пошаговая инструкция по безопасной покупке диплома о высшем образовании
Официальная покупка диплома вуза с сокращенной программой в Москве
Как приобрести аттестат о среднем образовании в Москве и других городах
Сколько стоит диплом высшего и среднего образования и как его получить?
Здесь можно преобрести сейф купить москва где купить сейф
вывод из запоя цены ростов на дону http://www.gonochki.forum24.ru/?1-10-0-00001135-000-0-0-1730726022 .
Promo Codes for subscription boxes http://skidki-i-kupony.ru .
вывод из запоя круглосуточно http://kryto.ukrbb.net/viewtopic.php?f=3&t=1164 .
вывод из запоя цены ростов на дону vip.rolevaya.info/viewtopic.php?id=6897 .
вывод из запоя стационар ростов http://www.mymoscow.forum24.ru/?1-6-0-00022906-000-0-0-1730726155/ .
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Официальная покупка диплома вуза с упрощенной программой обучения
Узнайте, как безопасно купить диплом о высшем образовании
Стоимость дипломов высшего и среднего образования и как избежать подделок
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Купить диплом старого образца, можно ли это сделать по быстрой схеме?
Тут можно преобрести сейфы для оружия оружейные сейфы для ружей
cabergoline 0.25mg generic – alesse drug buy alesse generic
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
Overview of Crypto Deal Verification and Conformity Services
In contemporary cryptocurrency industry, maintaining transfer openness and compliance with Anti-Money Laundering (AML) and KYC standards is vital. Here is an overview of popular platforms that provide solutions for crypto transaction tracking, verification, and fund security.
1. Tokenmetrics.com
Description: Token Metrics provides cryptocurrency assessment to examine likely scam threats. This platform enables users to check tokens before investment to evade likely fraudulent assets. Features:
– Danger evaluation.
– Suitable for holders seeking to steer clear of questionable or scam assets.
2. Metamask.Monitory.Center
Overview: Metamask Monitor Center enables users to verify their digital asset assets for questionable transactions and compliance conformity. Advantages:
– Checks coins for legitimacy.
– Offers alerts about likely resource restrictions on specific platforms.
– Delivers detailed insights after wallet linking.
3. Best Change
Description: Bestchange.ru is a service for tracking and validating crypto trade transactions, guaranteeing openness and transfer protection. Benefits:
– Deal and account observation.
– Restriction checks.
– Web-based interface; compatible with BTC and various different coins.
4. AMLCheck Bot
Overview: AMLCheck Bot is a holding observer and AML tool that utilizes artificial intelligence models to identify dubious actions. Features:
– Transaction tracking and user verification.
– Accessible via web version and chat bot.
– Works with digital assets such as BSC, BTC, DOGE, and additional.
5. AlfaBit
Description: AlphaBit offers comprehensive Anti-Money Laundering (AML) tools customized for the crypto market, assisting firms and banks in preserving compliance compliance. Features:
– Extensive compliance options and screenings.
– Adheres to up-to-date protection and compliance requirements.
6. AML Node
Summary: AML Node delivers anti-money laundering and customer identity solutions for cryptocurrency companies, such as transaction observing, restriction checks, and analysis. Benefits:
– Threat evaluation options and restriction validations.
– Important for ensuring safe firm activities.
7. Btrace.io
Summary: Btrace AML Crypto focuses on fund verification, providing transfer monitoring, sanctions checks, and assistance if you are a victim of fraud. Advantages:
– Useful help for asset retrieval.
– Transfer tracking and security tools.
Specialized USDT Verification Services
Our website also evaluates various sites that offer verification services for Tether transfers and wallets:
– **USDT TRC20 and ERC20 Verification:** Numerous sites provide thorough evaluations for USDT transactions, helping in the finding of suspicious transactions.
– **AML Screening for USDT:** Options are provided for observing for money laundering actions.
– **“Cleanliness” Screenings for Accounts:** Verification of transfer and holding purity is offered to identify likely risks.
**Wrap-up**
Choosing the right tool for validating and monitoring digital currency transfers is crucial for ensuring protection and regulatory compliance. By viewing our evaluations, you can choose the ideal solution for deal observation and resource security.
купить готовый диплом о среднем купить готовый диплом о среднем .
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
Всё о покупке аттестата о среднем образовании: полезные советы
вывод из запоя цены ростов на дону [url=https://vishivayu.ukrbb.net/viewtopic.php?f=12&t=13426/]https://vishivayu.ukrbb.net/viewtopic.php?f=12&t=13426/[/url] .
вывод из запоя в ростове вывод из запоя в ростове .
казино беларусь казино беларусь .
быстрый вывод из запоя ростов http://honey.ukrbb.net/viewtopic.php?f=45&t=16678/ .
вывод из запоя ростов и область pokupki.bestforums.org/viewtopic.php?f=7&t=24037 .
Как получить диплом техникума с упрощенным обучением в Москве официально
Полезные советы по безопасной покупке диплома о высшем образовании
dominion.listbb.ru/viewtopic.php?f=11&t=672
Быстрое обучение и получение диплома магистра – возможно ли это?
demo pg slot
Judul: Merasakan Pengalaman Memainkan dengan “PG Slot” di Situs Perjudian ImgToon.com
Dalam alam permainan kasino online, mesin slot telah jadi salah satu permainan yang paling diminati, terutama jenis PG Slot. Di antara beberapa situs kasino online, ImgToon.com menjadi tujuan pokok bagi pemain yang ingin menguji peruntungan mereka di beragam permainan slot, termasuk beberapa kategori populer seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Memulai Tanpa Risiko
Salah satu keistimewaan menarik yang ditawarkan oleh ImgToon.com adalah demo pg slot. Keistimewaan ini memungkinkan pemain untuk menguji berbagai jenis slot dari PG tanpa harus memasang taruhan sebenarnya. Dalam mode demo ini, Anda dapat menguji berbagai cara dan memahami proses permainan tanpa bahaya kehilangan uang. Ini adalah metode terbaik bagi pemula untuk terbiasa dengan permainan slot sebelum mengalihkan ke mode taruhan nyata.
Mode demo ini juga menyediakan Anda pemahaman tentang potensi kemenangan dan hadiah yang mungkin bisa Anda terima saat bermain dengan uang nyata. Pemain dapat menyusuri permainan tanpa cemas, menciptakan pengalaman bermain di PG Slot semakin menyenangkan dan bebas stres.
PG Slot Gacor: Prospek Besar Mendapatkan Kemenangan
PG Slot Gacor adalah kata populer di kalangan pemain slot yang merujuk pada slot yang sedang dalam fase memberi kemenangan tinggi atau lebih sering dikenal “gacor”. Di ImgToon.com, Anda dapat mendapatkan berbagai slot yang ada dalam kategori gacor ini. Slot ini dikenal memiliki peluang kemenangan lebih tinggi dan sering membagikan bonus besar, membuatnya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, perlu diingat bahwa “gacor” atau tidaknya sebuah slot dapat bergeser, karena permainan slot tergantung pada generator nomor acak (RNG). Dengan bermain secara rutin di ImgToon.com, Anda bisa mengenali pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan meningkatkan peluang Anda untuk menang.
RTP Slot: Faktor Esensial dalam Pemilihan Slot
Ketika membicarakan tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat krusial untuk dihitung. RTP Slot berkaitan pada persentase dari total taruhan yang akan dikirimkan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot dilengkapi dengan informasi RTP yang terang. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk mendapatkan kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat mengoptimalkan pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini membuat RTP sebagai indikator krusial bagi pemain yang mencari keuntungan dalam permainan kasino online.
Быстрая покупка диплома старого образца: возможные риски
terorizam.listbb.ru/viewtopic.php?f=3&t=699
SEC compliance check for cryptocurrency wallets
Summary of Digital Currency Transfer Validation and Conformity Options
In the current crypto industry, ensuring transfer transparency and adherence with AML and KYC regulations is essential. Following is an summary of popular sites that offer tools for digital asset transfer surveillance, verification, and fund protection.
1. Tokenmetrics.com
Description: Tokenmetrics delivers digital asset evaluation to evaluate likely risk risks. This platform enables users to examine cryptocurrencies before purchase to avoid likely scam resources. Features:
– Danger analysis.
– Suitable for holders seeking to steer clear of questionable or fraud projects.
2. Metamask.Monitory.Center
Summary: Metamask Monitor Center allows holders to review their crypto resources for questionable activity and standard adherence. Features:
– Validates tokens for purity.
– Offers alerts about potential fund blockages on particular platforms.
– Delivers comprehensive results after wallet linking.
3. Bestchange.com
Summary: Bestchange.ru is a platform for observing and checking crypto transaction transactions, providing clarity and transaction protection. Benefits:
– Deal and holding observation.
– Compliance validation.
– Web-based platform; supports BTC and several other digital assets.
4. AMLCheck Bot
Description: AMLchek is a investment monitor and compliance tool that utilizes machine learning models to identify dubious transactions. Features:
– Deal observation and personal verification.
– Accessible via web version and Telegram bot.
– Works with digital assets such as BSC, BTC, DOGE, and additional.
5. Alfabit AML
Overview: AlfaBit provides complete Anti-Money Laundering (AML) tools tailored for the digital currency market, assisting firms and financial organizations in ensuring compliance adherence. Features:
– Comprehensive AML tools and checks.
– Complies with current safety and regulatory standards.
6. Node AML
Description: AMLNode offers compliance and identification services for cryptocurrency businesses, which includes deal observing, compliance checks, and evaluation. Features:
– Risk analysis tools and compliance checks.
– Valuable for guaranteeing protected business processes.
7. Btrace.io
Summary: Btrace.AMLcrypto.io focuses on resource validation, providing deal tracking, restriction screenings, and assistance if you are a target of fraud. Benefits:
– Effective help for asset restoration.
– Deal monitoring and protection features.
Dedicated USDT Validation Solutions
Our platform also provides information on different platforms offering validation solutions for USDT deals and wallets:
– **USDT TRC20 and ERC20 Check:** Many services provide thorough screenings for USDT transfers, helping in the detection of suspicious actions.
– **AML Verification for USDT:** Solutions are provided for monitoring for suspicious transactions.
– **“Cleanliness” Validation for Wallets:** Checking of transfer and account purity is provided to find likely risks.
**Wrap-up**
Choosing the best platform for checking and observing crypto transactions is important for guaranteeing security and compliance conformity. By reading our recommendations, you can select the ideal solution for transaction monitoring and resource safety.
Парадокс, но купить диплом кандидата наук оказалось не так и сложно
Вопросы и ответы: можно ли быстро купить диплом старого образца?
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
Официальная покупка диплома вуза с сокращенной программой в Москве
Тут можно преобрести сейф несгораемый купить огнеупорный сейф купить
Покупка школьного аттестата с упрощенной программой: что важно знать
Legitimacy check for cryptocurrency transactions
Introduction of Cryptocurrency Transaction Validation and Compliance Solutions
In today’s crypto industry, guaranteeing transfer clarity and conformity with Anti-Laundering and Customer Identification standards is vital. Below is an outline of popular services that provide solutions for crypto transfer tracking, verification, and asset safety.
1. Token Metrics
Overview: Tokenmetrics delivers cryptocurrency evaluation to assess possible scam dangers. This platform enables users to examine coins prior to purchase to avoid possibly scam resources. Highlights:
– Danger evaluation.
– Suitable for investors looking to avoid questionable or scam assets.
2. Metamask Center
Description: Metamask Monitor Center enables holders to review their digital asset assets for questionable actions and regulatory compliance. Benefits:
– Verifies coins for purity.
– Delivers alerts about possible resource locks on particular platforms.
– Gives comprehensive insights after account linking.
3. BestChange.ru
Summary: Best Change is a service for observing and verifying crypto exchange transfers, guaranteeing openness and transfer security. Benefits:
– Deal and wallet monitoring.
– Sanctions checks.
– Internet portal; compatible with BTC and various different digital assets.
4. AMLCheck Bot
Overview: AMLchek is a holding monitor and compliance service that uses artificial intelligence methods to identify questionable transactions. Advantages:
– Transfer monitoring and user check.
– Available via web version and Telegram.
– Works with digital assets including BSC, BTC, DOGE, and other types.
5. AlfaBit
Description: AlphaBit delivers thorough Anti-Money Laundering (AML) tools customized for the cryptocurrency market, assisting businesses and banks in preserving compliance compliance. Features:
– Comprehensive anti-money laundering tools and checks.
– Complies with current safety and regulatory guidelines.
6. AMLNode
Overview: AMLNode provides anti-money laundering and KYC tools for crypto companies, including deal tracking, compliance screening, and evaluation. Features:
– Threat assessment solutions and compliance screenings.
– Useful for ensuring secure business processes.
7. Btrace.io
Description: Btrace AML Crypto focuses on asset validation, providing transfer observation, compliance screenings, and assistance if you are a victim of loss. Advantages:
– Useful assistance for fund recovery.
– Deal observation and security tools.
Exclusive USDT Validation Solutions
Our site also evaluates various platforms providing verification services for crypto deals and accounts:
– **USDT TRC20 and ERC20 Check:** Numerous services support thorough evaluations for USDT transactions, assisting in the identification of doubtful activity.
– **AML Validation for USDT:** Tools are offered for monitoring for fraudulent transactions.
– **“Cleanliness” Validation for Accounts:** Verification of transaction and holding “cleanliness” is available to identify likely threats.
**Summary**
Selecting the right platform for validating and observing crypto deals is crucial for providing protection and compliance compliance. By reading our reviews, you can find the most suitable service for transfer monitoring and fund safety.
Диплом техникума купить официально с упрощенным обучением в Москве
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
Тут можно преобрести купить шкаф для оружия оружейные шкафы и сейфы
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
Permanent makeup Austin
pg slot
Judul: Menikmati Pengalaman Memainkan dengan “PG Slot” di Situs Perjudian ImgToon.com
Dalam kehidupan permainan kasino online, slot telah menjadi salah satu permainan yang paling digemari, terutama jenis PG Slot. Di antara banyak situs kasino online, ImgToon.com menjadi tujuan pokok bagi peserta yang ingin menguji keberuntungan mereka di beragam permainan slot, termasuk beberapa kategori terfavorit seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Menjalani Tanpa adanya Risiko
Salah satu fungsi menarik yang disediakan oleh ImgToon.com adalah demo pg slot. Fitur ini mengizinkan pemain untuk mencoba berbagai jenis slot dari PG tanpa harus bertaruh taruhan sebenarnya. Dalam mode demo ini, Anda dapat menguji berbagai cara dan mengetahui proses permainan tanpa risiko kehilangan uang. Ini adalah metode terbaik bagi pemula untuk terbiasa dengan permainan slot sebelum berpindah ke mode taruhan nyata.
Mode demo ini juga memberikan Anda pandangan tentang potensi kemenangan dan bonus yang mungkin bisa Anda terima saat bermain dengan uang nyata. Pemain dapat mencari permainan tanpa ragu, menciptakan pengalaman bermain di PG Slot semakin membahagiakan dan bebas stres.
PG Slot Gacor: Prospek Besar Mendulang Kemenangan
PG Slot Gacor adalah istilah terkenal di kalangan pemain slot yang mengacu pada slot yang sedang dalam fase memberikan kemenangan tinggi atau lebih sering disebut “gacor”. Di ImgToon.com, Anda dapat menemukan berbagai slot yang termasuk dalam kategori gacor ini. Slot ini dikenal memiliki peluang kemenangan lebih tinggi dan sering membagikan bonus besar, membuatnya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, perlu diingat bahwa “gacor” atau tidaknya sebuah slot dapat beralih, karena permainan slot bergantung generator nomor acak (RNG). Dengan melakukan permainan secara rutin di ImgToon.com, Anda bisa menemukan pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan memperbesar peluang Anda untuk menang.
RTP Slot: Faktor Penting dalam Pemilahan Slot
Ketika membicarakan tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat krusial untuk diperhatikan. RTP Slot berkaitan pada persentase dari total taruhan yang akan dipulangkan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot diberi dengan informasi RTP yang jelas. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk mendapatkan kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat mengoptimalkan pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini membuat RTP sebagai indikator utama bagi pemain yang mencari keuntungan dalam permainan kasino online.
Удивительно, но купить диплом кандидата наук оказалось не так сложно
казино онлайн беларусь казино онлайн беларусь .
вывод из запоя круглосуточно ростов-на-дону http://rio16.ukrbb.net/viewtopic.php?f=3&t=1115 .
вывод из запоя круглосуточно http://www.severussnape.borda.ru/?1-4-0-00000313-000-0-0-1730648539/ .
Как оказалось, купить диплом кандидата наук не так уж и сложно
вывод из запоя в ростове на дону https://www.dubna.myqip.ru/?1-5-0-00000280-000-0-0-1730649298 .
анонимный вывод из запоя ростов http://www.chesskomi.borda.ru/?1-8-0-00003041-000-0-0-1730648765/ .
Вопросы и ответы: можно ли быстро купить диплом старого образца?
Приобретение диплома ПТУ с сокращенной программой обучения в Москве
marcoracing.dk/gde-kupit-attestat-za-9-klass-v-lipetske.html
Judul: Menikmati Pengalaman Bertaruh dengan “PG Slot” di Situs Kasino ImgToon.com
Dalam dunia permainan kasino online, permainan slot telah jadi salah satu permainan yang paling diminati, terutama jenis PG Slot. Di antara banyak situs kasino online, ImgToon.com adalah tujuan terbesar bagi peserta yang ingin menguji peruntungan mereka di beragam permainan slot, termasuk beberapa kategori populer seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Menjalani Tanpa adanya Risiko
Salah satu fitur menarik yang diberikan oleh ImgToon.com adalah demo pg slot. Fungsi ini memungkinkan pemain untuk menguji berbagai jenis slot dari PG tanpa harus bertaruh taruhan sebenarnya. Dalam mode demo ini, Anda dapat menguji berbagai cara dan mengerti mekanisme permainan tanpa ancaman kehilangan uang. Ini adalah langkah terbaik bagi pemain baru untuk beradaptasi dengan permainan slot sebelum beralih ke mode taruhan nyata.
Mode demo ini juga memberi Anda pemahaman tentang potensi kemenangan dan bonus yang mungkin bisa Anda terima saat bermain dengan uang nyata. Pemain dapat menjelajahi permainan tanpa ragu, membuat pengalaman bermain di PG Slot semakin membahagiakan dan bebas beban.
PG Slot Gacor: Peluang Besar Mendapatkan Kemenangan
PG Slot Gacor adalah sebutan terkenal di kalangan pemain slot yang menggunakan pada slot yang sedang dalam fase memberi kemenangan tinggi atau lebih sering disebut “gacor”. Di ImgToon.com, Anda dapat mendapatkan berbagai slot yang termasuk dalam kategori gacor ini. Slot ini dikenal memiliki peluang kemenangan lebih tinggi dan sering membagikan bonus besar, membuatnya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, perlu diingat bahwa “gacor” atau tidaknya sebuah slot dapat berubah, karena permainan slot bergantung generator nomor acak (RNG). Dengan melakukan permainan secara rutin di ImgToon.com, Anda bisa menemukan pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan menambah peluang Anda untuk menang.
RTP Slot: Faktor Penting dalam Pemilihan Slot
Ketika berbicara tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat penting untuk diperhatikan. RTP Slot berkaitan pada persentase dari total taruhan yang akan dipulangkan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot dilengkapi dengan informasi RTP yang terperinci. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk mendulang kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat mengelola pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini menyebabkan RTP sebagai indikator utama bagi pemain yang mencari keuntungan dalam permainan kasino online.
Тут можно преобрести сейф москва огнестойкий купить огнеупорный сейф
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Как не попасть впросак при покупке диплома колледжа или ПТУ в России
Купить диплом о среднем образовании в Москве и любом другом городе
Сервисный центр предлагает замена стекла infinix note 30 vip замена батареи infinix note 30 vip
Тут можно преобрести сейфы оружейные цена шкаф для оружия купить
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
whoah this blog is fantastic i really like studying your posts. Stay up the great work! You already know, many individuals are looking round for this information, you could aid them greatly.
https://www.fczulia.com/articulos/perevagy-led-linz-chomu-varto-investuvaty-v-yakisne-osvitlennya
Быстрое обучение и получение диплома магистра – возможно ли это?
Howdy just wanted to give you a quick heads up and let you know a few of the pictures aren’t loading correctly. I’m not sure why but I think its a linking issue. I’ve tried it in two different web browsers and both show the same results.
Можно ли купить аттестат о среднем образовании, основные моменты и вопросы
вывод. из. запоя. на. дому. ростов. http://www.angelladydety.getbb.ru/viewtopic.php?f=44&t=42897 .
вывод из запоя ростовская область http://alhambra.bestforums.org/viewtopic.php?f=2&t=46349 .
вывод из запоя ростов вывод из запоя ростов .
вывод из запоя на дому ростов круглосуточно вывод из запоя на дому ростов круглосуточно .
Judul: Mengalami Pengalaman Bertaruh dengan “PG Slot” di Situs Casino ImgToon.com
Dalam dunia permainan kasino online, permainan slot telah jadi salah satu permainan yang paling digemari, terutama jenis PG Slot. Di antara banyak situs kasino online, ImgToon.com adalah tujuan utama bagi pengguna yang ingin menguji peruntungan mereka di beragam permainan slot, termasuk beberapa kategori populer seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Memulai Bebas dari Risiko
Salah satu fungsi menarik yang disediakan oleh ImgToon.com adalah demo pg slot. Keistimewaan ini mengizinkan pemain untuk mencoba berbagai jenis slot dari PG tanpa harus bertaruh taruhan nyata. Dalam mode demo ini, Anda dapat menguji berbagai cara dan mengerti proses permainan tanpa ancaman kehilangan uang. Ini adalah langkah terbaik bagi pemain baru untuk mengenal dengan permainan slot sebelum beralih ke mode taruhan asli.
Mode demo ini juga memberikan Anda gambaran tentang potensi kemenangan dan hadiah yang mungkin bisa Anda dapatkan saat bermain dengan uang asli. Pemain dapat menyusuri permainan tanpa cemas, menjadikan pengalaman bermain di PG Slot semakin menyenangkan dan bebas beban.
PG Slot Gacor: Kesempatan Besar Mendapatkan Kemenangan
PG Slot Gacor adalah kata terkenal di kalangan pemain slot yang merujuk pada slot yang sedang dalam fase memberi kemenangan tinggi atau lebih sering dikenal “gacor”. Di ImgToon.com, Anda dapat mencari berbagai slot yang masuk dalam kategori gacor ini. Slot ini diakui memiliki peluang kemenangan lebih tinggi dan sering memberikan bonus besar, menjadikannya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, perlu diingat bahwa “gacor” atau tidaknya sebuah slot dapat berubah, karena permainan slot bergantung generator nomor acak (RNG). Dengan memainkan secara rutin di ImgToon.com, Anda bisa menemukan pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan memperbesar peluang Anda untuk menang.
RTP Slot: Faktor Esensial dalam Pencarian Slot
Ketika membicarakan tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat esensial untuk dihitung. RTP Slot berkaitan pada persentase dari total taruhan yang akan dipulangkan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot disertai dengan informasi RTP yang jelas. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk memperoleh kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat mengelola pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini membuat RTP sebagai indikator utama bagi pemain yang mencari keuntungan dalam permainan kasino online.
Как приобрести аттестат о среднем образовании в Москве и других городах
Как получить диплом техникума с упрощенным обучением в Москве официально
Полезные советы по безопасной покупке диплома о высшем образовании
Официальная покупка диплома вуза с упрощенной программой обучения
Тут можно преобрести купить огнеупорный сейф огнестойкие сейфы цена
купить дипломы техникума цена московская область 1oriks-diplom199.ru .
Тут можно преобрести купить сейф для ружья в москве оружейные сейфы и шкафы
Процесс получения диплома стоматолога: реально ли это сделать быстро?
гѓ—гѓ¬гѓ‰гѓ‹гѓі гЃ®иіје…Ґ – г‚ўг‚ёг‚№гѓгѓћг‚¤г‚·гѓігЃЇи–¬е±ЂгЃ§иІ·гЃ€г‚‹пјџ г‚ёг‚№гѓгѓћгѓѓг‚ЇгЃ®йЈІгЃїж–№гЃЁеЉ№жћњ
Как приобрести аттестат о среднем образовании в Москве и других городах
Как быстро получить диплом магистра? Легальные способы
Рекомендации по безопасной покупке диплома о высшем образовании
Здесь можно преобрести купить сейф интернете сейф купить москва
Blackjack Jugabet Per? https://jugabet777.com .
нарколог вывод из запоя ростов нарколог вывод из запоя ростов .
вывод из запоя в ростове на дону http://www.golosa.ukrbb.net/viewtopic.php?f=3&t=7466 .
вывод из запоя дешево ростов на дону http://ximki.ukrbb.net/viewtopic.php?f=12&t=3696 .
вывод из запоя срочно ростов вывод из запоя срочно ростов .
Сколько стоит получить диплом высшего и среднего образования легально?
twoplustwoequal.com/read-blog/48407
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Быстрая покупка диплома старого образца: возможные риски
Полезные советы по покупке диплома о высшем образовании без риска
rtp slot gacor terpercaya
Judul: Merasakan Pengalaman Bertaruh dengan “PG Slot” di Situs Casino ImgToon.com
Dalam alam permainan kasino online, slot telah menyusun salah satu permainan yang paling diminati, terutama jenis PG Slot. Di antara berbagai situs kasino online, ImgToon.com menjadi tujuan terbesar bagi pemain yang ingin mencoba keberuntungan mereka di beragam permainan slot, termasuk beberapa kategori terkenal seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Memulai Tanpa Risiko
Salah satu keistimewaan menarik yang diberikan oleh ImgToon.com adalah demo pg slot. Fitur ini mengizinkan pemain untuk menguji berbagai jenis slot dari PG tanpa harus bertaruh taruhan uang asli. Dalam mode demo ini, Anda dapat menguji berbagai strategi dan memahami mekanisme permainan tanpa bahaya kehilangan uang. Ini adalah langkah terbaik bagi pemula untuk mengenal dengan permainan slot sebelum berpindah ke mode taruhan asli.
Mode demo ini juga memberi Anda pandangan tentang potensi kemenangan dan imbalan yang mungkin bisa Anda dapatkan saat bermain dengan uang sebenarnya. Pemain dapat mencari permainan tanpa ragu, menciptakan pengalaman bermain di PG Slot semakin membahagiakan dan bebas stres.
PG Slot Gacor: Kesempatan Besar Mencapai Kemenangan
PG Slot Gacor adalah istilah terkemuka di kalangan pemain slot yang merujuk pada slot yang sedang dalam fase memberikan kemenangan tinggi atau lebih sering disebut “gacor”. Di ImgToon.com, Anda dapat menemukan berbagai slot yang ada dalam kategori gacor ini. Slot ini dikenal memiliki peluang kemenangan lebih tinggi dan sering memberikan bonus besar, menjadikannya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, perlu diingat bahwa “gacor” atau tidaknya sebuah slot dapat bergeser, karena permainan slot bergantung generator nomor acak (RNG). Dengan memainkan secara rutin di ImgToon.com, Anda bisa menemukan pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan meningkatkan peluang Anda untuk menang.
RTP Slot: Faktor Penting dalam Pencarian Slot
Ketika membicarakan tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat penting untuk dipertimbangkan. RTP Slot merujuk pada persentase dari total taruhan yang akan dikirimkan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot dilengkapi dengan informasi RTP yang terperinci. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk memperoleh kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat mengoptimalkan pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini menyebabkan RTP sebagai indikator utama bagi pemain yang mencari keuntungan dalam permainan kasino online.
pg slot gacor terpercaya
Judul: Merasakan Pengalaman Memainkan dengan “PG Slot” di Situs Casino ImgToon.com
Dalam alam permainan kasino online, slot telah menjadi salah satu permainan yang paling disukai, terutama jenis PG Slot. Di antara beberapa situs kasino online, ImgToon.com adalah tujuan terbesar bagi pemain yang ingin menguji peruntungan mereka di banyak permainan slot, termasuk beberapa kategori terfavorit seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Memulai Tanpa Risiko
Salah satu fitur menarik yang ditawarkan oleh ImgToon.com adalah demo pg slot. Fitur ini memberikan pemain untuk memainkan berbagai jenis slot dari PG tanpa harus bertaruh taruhan uang asli. Dalam mode demo ini, Anda dapat memeriksa berbagai strategi dan mengerti proses permainan tanpa risiko kehilangan uang. Ini adalah metode terbaik bagi pemain baru untuk beradaptasi dengan permainan slot sebelum beralih ke mode taruhan nyata.
Mode demo ini juga memberi Anda pemahaman tentang potensi kemenangan dan hadiah yang mungkin bisa Anda terima saat bermain dengan uang asli. Pemain dapat menjelajahi permainan tanpa ragu, menjadikan pengalaman bermain di PG Slot semakin menyenangkan dan bebas tekanan.
PG Slot Gacor: Prospek Besar Mencapai Kemenangan
PG Slot Gacor adalah kata populer di kalangan pemain slot yang merujuk pada slot yang sedang dalam fase memberikan kemenangan tinggi atau lebih sering dikenal “gacor”. Di ImgToon.com, Anda dapat menemukan berbagai slot yang ada dalam kategori gacor ini. Slot ini dikenal memiliki peluang kemenangan lebih tinggi dan sering memberikan bonus besar, membuatnya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, penting diingat bahwa “gacor” atau tidaknya sebuah slot dapat beralih, karena permainan slot bergantung generator nomor acak (RNG). Dengan bermain secara rutin di ImgToon.com, Anda bisa mengenali pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan meningkatkan peluang Anda untuk menang.
RTP Slot: Faktor Penting dalam Pencarian Slot
Ketika mendiskusikan tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat krusial untuk dipertimbangkan. RTP Slot merujuk pada persentase dari total taruhan yang akan dikirimkan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot disertai dengan informasi RTP yang terang. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk memperoleh kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat memaksimalkan pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini menjadikan RTP sebagai indikator utama bagi pemain yang mencari keuntungan dalam permainan kasino online.
Judul: Mengalami Pengalaman Memainkan dengan “PG Slot” di Situs Casino ImgToon.com
Dalam kehidupan permainan kasino online, mesin slot telah menyusun salah satu permainan yang paling diminati, terutama jenis PG Slot. Di antara beberapa situs kasino online, ImgToon.com menjadi tujuan terbesar bagi peserta yang ingin menguji nasib mereka di beragam permainan slot, termasuk beberapa kategori terkenal seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Menjalani Bebas dari Risiko
Salah satu keistimewaan menarik yang ditawarkan oleh ImgToon.com adalah demo pg slot. Keistimewaan ini mengizinkan pemain untuk memainkan berbagai jenis slot dari PG tanpa harus menempatkan taruhan nyata. Dalam mode demo ini, Anda dapat memeriksa berbagai taktik dan mengerti mekanisme permainan tanpa ancaman kehilangan uang. Ini adalah metode terbaik bagi pemula untuk beradaptasi dengan permainan slot sebelum berpindah ke mode taruhan nyata.
Mode demo ini juga menyediakan Anda pemahaman tentang potensi kemenangan dan hadiah yang mungkin bisa Anda peroleh saat bermain dengan uang asli. Pemain dapat menjelajahi permainan tanpa cemas, membuat pengalaman bermain di PG Slot semakin mengasyikkan dan bebas tekanan.
PG Slot Gacor: Kesempatan Besar Mendapatkan Kemenangan
PG Slot Gacor adalah kata terkenal di kalangan pemain slot yang merujuk pada slot yang sedang dalam fase memberi kemenangan tinggi atau lebih sering dikenal “gacor”. Di ImgToon.com, Anda dapat mendapatkan berbagai slot yang termasuk dalam kategori gacor ini. Slot ini terkenal memiliki peluang kemenangan lebih tinggi dan sering membagikan bonus besar, menjadikannya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, harus diingat bahwa “gacor” atau tidaknya sebuah slot dapat beralih, karena permainan slot bergantung generator nomor acak (RNG). Dengan memainkan secara rutin di ImgToon.com, Anda bisa mengidentifikasi pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan memperbesar peluang Anda untuk menang.
RTP Slot: Faktor Krucial dalam Pemilahan Slot
Ketika membicarakan tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat krusial untuk dipertimbangkan. RTP Slot mengacu pada persentase dari total taruhan yang akan dikirimkan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot disertai dengan informasi RTP yang terang. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk mendapatkan kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat mengoptimalkan pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini menyebabkan RTP sebagai indikator penting bagi pemain yang mencari keuntungan dalam permainan kasino online.
rtp slot terpercaya
Judul: Menikmati Pengalaman Memainkan dengan “PG Slot” di Situs Casino ImgToon.com
Dalam alam permainan kasino online, permainan slot telah menyusun salah satu permainan yang paling digemari, terutama jenis PG Slot. Di antara banyak situs kasino online, ImgToon.com adalah tujuan terbesar bagi peserta yang ingin mencoba peruntungan mereka di beragam permainan slot, termasuk beberapa kategori terkenal seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Menjalani Tanpa adanya Risiko
Salah satu fungsi menarik yang disediakan oleh ImgToon.com adalah demo pg slot. Keistimewaan ini mengizinkan pemain untuk menguji berbagai jenis slot dari PG tanpa harus memasang taruhan sebenarnya. Dalam mode demo ini, Anda dapat menguji berbagai strategi dan memahami sistem permainan tanpa risiko kehilangan uang. Ini adalah cara terbaik bagi orang baru untuk beradaptasi dengan permainan slot sebelum berpindah ke mode taruhan sebenarnya.
Mode demo ini juga memberikan Anda pandangan tentang potensi kemenangan dan imbalan yang mungkin bisa Anda peroleh saat bermain dengan uang nyata. Pemain dapat mencari permainan tanpa cemas, menciptakan pengalaman bermain di PG Slot semakin mengasyikkan dan bebas stres.
PG Slot Gacor: Prospek Besar Mendapatkan Kemenangan
PG Slot Gacor adalah sebutan terkemuka di kalangan pemain slot yang menggunakan pada slot yang sedang dalam fase memberikan kemenangan tinggi atau lebih sering dikenal “gacor”. Di ImgToon.com, Anda dapat mendapatkan berbagai slot yang termasuk dalam kategori gacor ini. Slot ini diakui memiliki peluang kemenangan lebih tinggi dan sering memberikan bonus besar, menjadikannya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, harus diingat bahwa “gacor” atau tidaknya sebuah slot dapat beralih, karena permainan slot tergantung pada generator nomor acak (RNG). Dengan memainkan secara rutin di ImgToon.com, Anda bisa mengidentifikasi pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan memperbesar peluang Anda untuk menang.
RTP Slot: Faktor Penting dalam Pencarian Slot
Ketika berbicara tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat penting untuk dihitung. RTP Slot mengacu pada persentase dari total taruhan yang akan dikembalikan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot diberi dengan informasi RTP yang terang. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk mendapatkan kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat memaksimalkan pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini menjadikan RTP sebagai indikator penting bagi pemain yang mencari keuntungan dalam permainan kasino online.
Тут можно преобрести ящик для оружия купить сейфы для оружия купить
Тут можно преобрести сейф огнестойкий купить несгораемый сейф
Judul: Mengalami Pengalaman Bertaruh dengan “PG Slot” di Situs Kasino ImgToon.com
Dalam dunia permainan kasino online, mesin slot telah menjadi salah satu permainan yang paling disukai, terutama jenis PG Slot. Di antara berbagai situs kasino online, ImgToon.com menjadi tujuan terbesar bagi pemain yang ingin mencoba keberuntungan mereka di berbagai permainan slot, termasuk beberapa kategori populer seperti demo pg slot, pg slot gacor, dan RTP slot.
Demo PG Slot: Memulai Tanpa adanya Risiko
Salah satu fungsi menarik yang ditawarkan oleh ImgToon.com adalah demo pg slot. Fitur ini memungkinkan pemain untuk menguji berbagai jenis slot dari PG tanpa harus memasang taruhan nyata. Dalam mode demo ini, Anda dapat menguji berbagai taktik dan mengerti sistem permainan tanpa risiko kehilangan uang. Ini adalah cara terbaik bagi pemula untuk mengenal dengan permainan slot sebelum beralih ke mode taruhan sebenarnya.
Mode demo ini juga menyediakan Anda pandangan tentang potensi kemenangan dan bonus yang mungkin bisa Anda terima saat bermain dengan uang nyata. Pemain dapat mencari permainan tanpa khawatir, menciptakan pengalaman bermain di PG Slot semakin membahagiakan dan bebas stres.
PG Slot Gacor: Kesempatan Besar Mendapatkan Kemenangan
PG Slot Gacor adalah sebutan populer di kalangan pemain slot yang merujuk pada slot yang sedang dalam fase memberikan kemenangan tinggi atau lebih sering dikenal “gacor”. Di ImgToon.com, Anda dapat mendapatkan berbagai slot yang masuk dalam kategori gacor ini. Slot ini dikenal memiliki peluang kemenangan lebih tinggi dan sering memberikan bonus besar, membuatnya pilihan utama bagi para pemain yang ingin memperoleh keuntungan maksimal.
Namun, penting diingat bahwa “gacor” atau tidaknya sebuah slot dapat bergeser, karena permainan slot tergantung pada generator nomor acak (RNG). Dengan melakukan permainan secara rutin di ImgToon.com, Anda bisa menemukan pola atau waktu yang tepat untuk memainkan PG Slot Gacor dan menambah peluang Anda untuk menang.
RTP Slot: Faktor Esensial dalam Pemilihan Slot
Ketika membicarakan tentang slot, istilah RTP (Return to Player) adalah faktor yang sangat krusial untuk dipertimbangkan. RTP Slot merujuk pada persentase dari total taruhan yang akan dipulangkan kepada pemain dalam jangka panjang. Di ImgToon.com, setiap permainan PG Slot diberi dengan informasi RTP yang jelas. Semakin tinggi persentase RTP, semakin besar peluang pemain untuk mendapatkan kembali sebagian besar dari taruhan mereka.
Dengan memilih PG Slot yang memiliki RTP tinggi, pemain dapat mengelola pengeluaran mereka dan memiliki peluang yang lebih baik untuk menang dalam jangka panjang. Ini menyebabkan RTP sebagai indikator krusial bagi pemain yang mencari keuntungan dalam permainan kasino online.
Быстрая схема покупки диплома старого образца: что важно знать?
Всё, что нужно знать о покупке аттестата о среднем образовании без рисков
Купить диплом ВУЗа России
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Как получить диплом техникума официально и без лишних проблем
Как купить диплом о высшем образовании с минимальными рисками
Полезные советы по безопасной покупке диплома о высшем образовании
Узнай все о варикоцеле причины степени варикоцеле
. http://www.exeideas.com/2020/07/reading-progress-bar-in-blogger.html#comment-428550 .
вывод из запоя стационарно ростов https://ukroenergo.ukrbb.net/viewtopic.php?f=13&t=21376 .
вывод из запоя ростов и область https://www.uaforum.ukrbb.net/viewtopic.php?f=13&t=3230 .
Как приобрести диплом техникума с минимальными рисками
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Легальная покупка диплома ПТУ с сокращенной программой обучения
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали сервисный центр xiaomi, можете посмотреть на сайте: сервисный центр xiaomi
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Купить диплом магистра оказалось возможно, быстрое обучение и диплом на руки
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Узнай все о варикоцеле причины возникновения варикоцеле 3 степени
Game keys
Explore a World of Virtual Chances with Items4Play
At Items4Play, we deliver a vibrant hub for players to buy or exchange accounts, virtual items, and services for widely played titles. Whether you are looking to upgrade your game resources or wanting to profit from your account, our site delivers a easy, secure, and profitable experience.
Why Select Items4Games?
**Comprehensive Title Catalog**: Browse a extensive variety of titles, from thrilling games like Battleground and Call of Duty to captivating role-playing games such as ARK: Survival Evolved and Genshin. We cover all games, guaranteeing no enthusiast is left behind.
**Selection of Features**: Our products cover account purchases, in-game currency, rare collectibles, milestones, and mentoring options. If you are looking for help gaining levels or obtaining exclusive rewards, we’ve got you covered.
**User-friendly**: Browse without hassle through our systematized marketplace, organized alphabetically to find just the item you are looking for with ease.
**Safe Deals**: We prioritize your safety. All transactions on our marketplace are conducted with the highest safeguarding to guard your personal and monetary data.
**Key Points from Our Inventory**
– **Action and Exploration**: Games like ARK and DayZ let you explore tough environments with top-notch goods and accesses for sale.
– **Adventure and Adventure**: Boost your performance in titles like Clash Royale and Wonders Age with virtual money and services.
– **eSports Competitions**: For competitive enthusiasts, enhance your skills with coaching and account upgrades for Valored, Dota, and League of Legends.
**A Marketplace Built for Gamers**
Backed by Apex Technologies, a reliable company certified in Kazakh Republic, Items4Play is a market where playtime aspirations become real. From buying advance keys for the latest games to getting unique in-game treasures, our marketplace meets every player’s requirement with professionalism and efficiency.
Become part of the group today and elevate your game experience!
For inquiries or guidance, reach out to us at **support@items4games.com**. Let’s all enjoy gaming, together!
вывод из запоя на дому ростов на дону http://obovsem.rolevaya.info/viewtopic.php?id=3669 .
выезд нарколога на дом http://avtomobili.creartuforo.com/viewtopic.php?id=731/ .
нарколог на дом анонимно нарколог на дом анонимно .
Аттестат школы купить официально с упрощенным обучением в Москве
Быстрая схема покупки диплома старого образца: что важно знать?
Как приобрести диплом о среднем образовании в Москве и других городах
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Как приобрести аттестат о среднем образовании в Москве и других городах
Быстрая схема покупки диплома старого образца: что важно знать?
Стоимость дипломов высшего и среднего образования и процесс их получения
rabota-vakansii-spb.ru/kupit-attestat-o-srednem-obrazovanii-v-krasnodare.html
Купить диплом экономиста – оптимальное решение
платный нарколог на дом spilkuvannya.rolevaya.com/viewtopic.php?id=66 .
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Explore a World of Virtual Chances with ItemsforGames
At Items4Play, we provide a active marketplace for gamers to acquire or sell gaming accounts, virtual items, and features for some of the most popular titles. If you are looking to improve your gaming arsenal or wanting to profit from your profile, our site delivers a easy, secure, and rewarding process.
Why Choose Items4Games?
**Comprehensive Game Library**: Explore a large variety of titles, from intense games such as Warzone and COD to captivating role-playing games such as ARK: Survival Evolved and Genshin. We have all games, making sure no player is overlooked.
**Range of Features**: Our offerings cover game account acquisitions, in-game currency, rare collectibles, achievements, and training services. If you need assistance leveling up or obtaining exclusive rewards, we’ve got you covered.
**Ease of Use**: Explore easily through our structured platform, organized by order to get precisely the item you need with ease.
**Protected Transactions**: We prioritize your security. All transactions on our platform are conducted with the top security to secure your confidential and payment data.
**Key Points from Our Collection**
– **Survival and Survival**: Titles ARK: Survival Evolved and Day-Z give you the chance to dive into exciting worlds with top-notch gear and passes available.
– **Tactical and Questing**: Enhance your experience in games like Clash Royale and Age of Wonders 4 with virtual money and options.
– **eSports Competitions**: For serious enthusiasts, boost your abilities with mentoring and account upgrades for Valorant, Dota, and Legends.
**A Marketplace Designed for Fans**
Supported by Apex Technologies, a trusted business certified in Kazakh Republic, ItemsforGames is a market where video game wishes become real. From purchasing advance passes for the newest titles to locating hard-to-find in-game treasures, our marketplace fulfills every gaming requirement with professionalism and efficiency.
Sign up for the group today and elevate your game experience!
For inquiries or guidance, email us at **support@items4games.com**. Let’s all improve the game, together!
Тут можно преобрести оружейные сейфы купить в москве сейфы оружейные
Узнай все о рецидив варикоцеле лапароскопия варикоцеле
Сколько стоит диплом высшего и среднего образования и как это происходит?
Рекомендации по безопасной покупке диплома о высшем образовании
productinn.mn.co/posts/69577092
Как приобрести аттестат о среднем образовании в Москве и других городах
Полезные советы по покупке диплома о высшем образовании без риска
Диплом пту купить официально с упрощенным обучением в Москве
Официальная покупка школьного аттестата с упрощенным обучением в Москве
Как быстро получить диплом магистра? Легальные способы
Как приобрести диплом о среднем образовании в Москве и других городах
バイアグラ通販で買えますか – г‚їгѓЂгѓ©гѓ•г‚Јгѓ« и–¬е±ЂгЃ§иІ·гЃ€г‚‹ г‚їгѓЂгѓ©гѓ•г‚Јгѓ« гЃ©гЃ“гЃ§иІ·гЃ€г‚‹
Быстрая схема покупки диплома старого образца: что важно знать?
Купить диплом судоводителя
Аттестат школы купить официально с упрощенным обучением в Москве
Полезные советы по безопасной покупке диплома о высшем образовании
Официальная покупка диплома вуза с сокращенной программой в Москве
нарколог краснодар http://www.masa.forum24.ru/?1-16-0-00002626-000-0-0-1730730156 .
электрокарнизы купить в москве электрокарнизы купить в москве .
нарколог на дом круглосуточно https://automobilist.forum24.ru/?1-19-0-00000138-000-0-0-1730729674 .
нарколог на дом краснодар http://motik13.0pk.me/viewtopic.php?id=1995 .
частный нарколог на дом https://setter.borda.ru/?1-7-0-00000673-000-0-0-1730729894 .
Howdy just wanted to give you a quick heads up and let you know a few of the images aren’t loading properly. I’m not sure why but I think its a linking issue. I’ve tried it in two different browsers and both show the same outcome.
best online casino
Как получить диплом техникума с упрощенным обучением в Москве официально
mir.4admins.ru/posting.php?mode=post&f=10&sid=a4d7fd52f9bebd0e2ec22b5413e65d8d
Покупка школьного аттестата с упрощенной программой: что важно знать
Быстрая схема покупки диплома старого образца: что важно знать?
Стоимость дипломов высшего и среднего образования и как избежать подделок
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Как получить диплом техникума официально и без лишних проблем
Узнай все о удаление полипа на шейке маткиоперация по удалению полипа в матке
Как приобрести диплом о среднем образовании в Москве и других городах
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Аттестат школы купить официально с упрощенным обучением в Москве
Купить диплом в России, предлагает наша компания
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
купить программу 1с торговля купить программу 1с торговля .
вызов нарколога на дом краснодар rubiz.forum.cool/viewtopic.php?id=3746 .
выезд нарколога на дом http://www.forumbar.anihub.me/viewtopic.php?id=9753 .
нарколог на дом круглосуточно http://www.krut.forumno.com/viewtopic.php?id=6026 .
частный нарколог на дом https://obovsem.rolevaya.info/viewtopic.php?id=3674/ .
Официальная покупка диплома вуза с упрощенной программой обучения
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Легальная покупка школьного аттестата с упрощенной программой обучения
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Официальное получение диплома техникума с упрощенным обучением в Москве
Где и как купить диплом о высшем образовании без лишних рисков
Explore a World of Gaming Chances with Items4Play
At Items4Games, we deliver a dynamic platform for enthusiasts to purchase or sell gaming accounts, virtual items, and features for top games. Whether you are seeking to improve your game inventory or looking to monetize your game account, our site delivers a easy, protected, and valuable journey.
Reasons to Select ItemsforGames?
**Comprehensive Title Catalog**: Browse a large variety of titles, from thrilling adventures such as Battlefield and COD to immersive role-playing games such as ARK: Survival Evolved and Genshin. We have everything, making sure no enthusiast is overlooked.
**Selection of Features**: Our products feature profile buys, credits, rare collectibles, achievements, and training sessions. Whether you want guidance improving or obtaining special rewards, we are here to help.
**User-friendly**: Browse easily through our systematized site, categorized by order to get exactly what you want fast.
**Safe Exchanges**: We focus on your protection. All exchanges on our platform are processed with the highest safeguarding to secure your personal and monetary data.
**Key Points from Our Collection**
– **Survival and Adventure**: Titles ARK: Survival Evolved and DayZ give you the chance to explore exciting worlds with high-quality items and accesses on offer.
– **Adventure and Adventure**: Boost your experience in adventures like Royal Clash and Wonders Age with in-game currencies and services.
– **Competitive Play**: For eSports enthusiasts, enhance your technique with training and level-ups for Valored, DotA, and Legends.
**A Hub Designed for Players**
Backed by ApexTech Innovations, a trusted business registered in Kazakh Republic, Items4Games is a hub where gaming aspirations become real. From acquiring pre-order codes for the latest titles to finding rare in-game treasures, our marketplace meets every gamer’s need with skill and reliability.
Become part of the group right away and elevate your gaming experience!
For inquiries or guidance, reach out to us at **support@items4games.com**. Together, let’s game better, together!
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
промокод продамус https://vip.rolevaya.info/viewtopic.php?id=7107#p1 .
срочная помощь вывод из запоя краснодар http://www.tatuheart.ukrbb.net/viewtopic.php?f=8&t=15068/ .
вывод из запоя дешево краснодар вывод из запоя дешево краснодар .
быстрый анонимный вывод из запоя на дому быстрый анонимный вывод из запоя на дому .
вывод из запоя краснодар на дому http://belbeer.borda.ru/?1-6-0-00000757-000-0-0-1730745253 .
вывод из запоя цены на дому краснодар http://www.dolgoprudni.rusff.me/viewtopic.php?id=3065#p8958 .
Реально ли приобрести диплом стоматолога? Основные шаги
Аттестат 11 класса купить официально с упрощенным обучением в Москве
Узнай все о операция на исправление перегородки носапластика перегородки носа
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
Официальная покупка школьного аттестата с упрощенным обучением в Москве
Полезные советы по безопасной покупке диплома о высшем образовании
Как избежать рисков при покупке диплома колледжа или ВУЗа в России
Возможно ли купить диплом стоматолога, и как это происходит
Стоимость дипломов высшего и среднего образования и как избежать подделок
Покупка диплома о среднем полном образовании: как избежать мошенничества?
гѓ—гѓ¬гѓ‰гѓ‹гѓі йЈІгЃїж–№ – イソトレチノイン処方 г‚¤г‚Ѕгѓ€гѓ¬гѓЃгѓЋг‚¤гѓійЊ 20 mg еј·гЃ•
Узнайте, как приобрести диплом о высшем образовании без рисков
Купить диплом Барнаул
Как оказалось, купить диплом кандидата наук не так уж и сложно
Узнай все о увеличение полового члена москва операции по увеличению полового члена
вывод из запоя в стационаре воронежа вывод из запоя в стационаре воронежа .
вывод из запоя капельница https://sergiev.0pk.me/viewtopic.php?id=3461 .
фонбет беларусь фонбет беларусь .
fonbet by fonbet by .
Реально ли приобрести диплом стоматолога? Основные шаги
Как официально приобрести аттестат 11 класса с минимальными затратами времени
Реально ли приобрести диплом стоматолога? Основные этапы
Всё, что нужно знать о покупке аттестата о среднем образовании
Аттестат 11 класса купить официально с упрощенным обучением в Москве
Покупка диплома о среднем полном образовании: как избежать мошенничества?
politikforum.ru/member.php?u=13385920
Официальное получение диплома техникума с упрощенным обучением в Москве
Официальная покупка диплома вуза с упрощенной программой обучения
Реально ли приобрести диплом стоматолога? Основные шаги
Как не стать жертвой мошенников при покупке диплома о среднем полном образовании
Приобретение диплома ПТУ с сокращенной программой обучения в Москве
вывод из запоя в стационаре анонимно http://golosa.ukrbb.net/viewtopic.php?f=3&t=7471 .
вывод из запоя в стационаре воронежа vishivayu.ukrbb.net/viewtopic.php?f=12&t=13444 .
вывод из запоя в стационаре анонимно https://uaportal.ukrbb.net/viewtopic.php?f=2&t=3720 .
вывод из запоя в воронеже http://www.alhambra.bestforums.org/viewtopic.php?f=2&t=46417 .
лечение наркозависимости в стационаре лечение наркозависимости в стационаре .
Можно ли купить аттестат о среднем образовании? Основные рекомендации
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали сервисный центр lg, можете посмотреть на сайте: сервисный центр lg
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Быстрая схема покупки диплома старого образца: что важно знать?
Реально ли приобрести диплом стоматолога? Основные этапы
Всё, что нужно знать о покупке аттестата о среднем образовании без рисков
Реально ли приобрести диплом стоматолога? Основные этапы
Быстрая схема покупки диплома старого образца: что важно знать?
Сколько стоит диплом высшего и среднего образования и как его получить?
Приобретение школьного аттестата с официальным упрощенным обучением в Москве
вывод из запоя в стационаре вывод из запоя в стационаре .
Покупка диплома о среднем полном образовании: как избежать мошенничества?
лечение наркозависимости в стационаре http://superogorod.ucoz.org/forum/2-2086-1/ .
вывод из запоя в воронеже http://www.gaslo.ukrbb.net/viewtopic.php?f=13&t=3413 .
вывод из запоя в стационаре анонимно вывод из запоя в стационаре анонимно .
富遊娛樂城出金教學指南：全面解析
富遊娛樂城是一個備受信賴的線上娛樂平台，提供高效、安全的出金服務。以下是詳細的指南，幫助玩家快速掌握提款流程，並瞭解相關注意事項和解決問題的方法。
1. 富遊娛樂城出金步驟
登入平台：使用【富遊APP】或【富遊官網】。
選擇存取款功能：點擊右下角的【存取款】按鈕。
點擊提款：初次使用需完成帳戶實名驗證。
輸入提款金額：選擇已綁定的取款帳戶。
提交申請：送出後等待審核，款項將快速到賬。
2. 娛樂城出金/提款注意事項
實名認證：確保完成帳戶認證，否則無法提款。
存款流水要求：每次提款需完成至少1倍的存款流水條件。
活動流水條件：若參與優惠活動，需依照活動規定完成對應的流水倍數。
3. 娛樂城流水如何計算？
流水計算是出金的重要條件，其公式如下：
存款金額 / 優惠金額 X 流水倍數 = 可提領流水量
例子說明：
玩家小明存入1,000元，參與一項需達到3倍流水的優惠活動：
需要下注金額 = 1,000元 x 3倍 = 3,000元。
如果累計下注金額為2,000元，則還需下注1,000元以達到流水要求。
一旦流水達標，即可提款。
4. 若遇到不出金問題怎麼辦？
選擇可靠平台：避免詐騙娛樂城，富遊娛樂城以出金速度快、保障用戶資金安全聞名。
聯繫客服：若出現問題，可透過LINE官方客服獲得即時協助。
結論
富遊娛樂城以其安全高效的出金系統和透明的規範，為玩家提供優質的服務。遵循上述指引，並確保完成所有條件，玩家即可輕鬆體驗順暢的提款過程。
Официальная покупка диплома ВУЗа с упрощенной программой обучения
Как получить диплом стоматолога быстро и официально
Как быстро получить диплом магистра? Легальные способы
Купить диплом ВУЗа России
Как купить диплом о высшем образовании с минимальными рисками
THA娛樂城
THA娛樂城與九州娛樂簡介
THA娛樂城是九州娛樂旗下的一個知名線上娛樂平台，致力於為玩家提供多元化且優質的娛樂服務。九州娛樂是亞洲地區領先的線上娛樂品牌，長期專注於打造穩定、公平且充滿樂趣的遊戲環境，旗下擁有多個知名娛樂平台，而THA娛樂城便是其中的一個旗艦產品。以下將詳細介紹THA娛樂城的特色與服務。
THA娛樂城的遊戲種類
THA娛樂城為玩家提供了多樣化的遊戲選擇，滿足不同玩家的需求與興趣，包括以下幾大類別：
1. 體育投注
體育迷可以在THA娛樂城享受豐富的體育賽事投注，涵蓋足球、籃球、網球等多項國際體育比賽。平台提供即時賠率和多種投注選項，讓玩家隨時掌握比賽動態並進行下注。
2. 真人娛樂
真人娛樂區提供即時互動的遊戲體驗，玩家可透過直播技術與真人荷官互動，遊玩如百家樂、輪盤、骰寶等經典遊戲。這不僅增添了真實感，更讓玩家有身臨其境的感受。
3. 電子老虎機
THA娛樂城匯集了多款高人氣的電子老虎機遊戲，從經典水果機到新潮主題機，皆配備精美的畫面與流暢的操作介面，為玩家帶來無限樂趣。
4. 捕魚遊戲
捕魚遊戲是許多玩家的最愛，THA娛樂城提供多種精美場景和豐富玩法的捕魚遊戲，玩家可以挑戰高額獎勵，享受射擊與策略結合的獨特樂趣。
5. 彩票與其他遊戲
除了以上幾類，平台還提供彩票遊戲及其他創新型娛樂遊戲，適合喜歡嘗試新鮮玩法的玩家。
九州娛樂的技術支持
作為THA娛樂城的母公司，九州娛樂以其強大的技術實力與嚴謹的管理體系為平台提供支持。九州娛樂採用國際領先的安全加密技術，確保玩家的個人資訊與交易數據得到妥善保護。此外，平台的遊戲結果皆經過嚴格的隨機性測試與第三方機構認證，保證公平公正。
優質的會員服務
THA娛樂城致力於打造一個高品質的會員體驗，其服務特色包括：
– 優惠活動
平台定期推出多種促銷活動，如新會員註冊禮金、存款返利、週週回饋等，讓玩家享受更多的遊戲資金。
– 快速出入金
平台提供便捷且快速的存提款服務，玩家可以安心進行資金操作，且無需擔心延遲問題。
– 24小時客戶服務
為了確保玩家的需求能即時被解決，THA娛樂城提供全年無休的客服支援，無論是遊戲問題還是技術諮詢，客服團隊都能快速回應。
與其他平台的區別
THA娛樂城之所以能在眾多線上娛樂平台中脫穎而出，不僅因其豐富的遊戲種類與高品質服務，更在於它所帶來的獨特價值：
1. 品牌信譽
作為九州娛樂旗下的品牌，THA娛樂城擁有長期積累的良好信譽，是許多玩家的首選。
2. 創新與多樣性
平台不斷推出新遊戲與創意玩法，讓玩家始終保持新鮮感。
3. 本地化服務
THA娛樂城深諳玩家需求，提供多語言支援與符合本地習慣的服務，提升玩家的使用便利性。
未來展望
隨著線上娛樂行業的快速發展，THA娛樂城也在持續進步與創新，力求為玩家帶來更多驚喜。無論是透過引進新的遊戲技術、擴展遊戲種類，還是改善服務品質，THA娛樂城都希望成為每位玩家的最佳娛樂夥伴。
總結來說，THA娛樂城憑藉其豐富的遊戲內容、可靠的技術支持以及優質的會員服務，已在亞洲娛樂市場佔有一席之地。如果您正在尋找一個結合刺激與信賴的娛樂平台，那麼THA娛樂城絕對值得一試。
Пошаговая инструкция по официальной покупке диплома о высшем образовании
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали сервисный центр huawei, можете посмотреть на сайте: сервисный центр huawei
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Можно ли купить аттестат о среднем образовании, основные моменты и вопросы
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали официальный сервисный центр philips, можете посмотреть на сайте: сервисный центр philips в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
Всё, что нужно знать о покупке аттестата о среднем образовании без рисков
Быстрое обучение и получение диплома магистра – возможно ли это?
Стоимость дипломов высшего и среднего образования и как избежать подделок
Аттестат школы купить официально с упрощенным обучением в Москве
Как правильно купить диплом колледжа и пту в России, подводные камни
вывод из запоя цена http://www.familyportal.forumrom.com/viewtopic.php?id=28575 .
Как получить диплом техникума официально и без лишних проблем
Сколько стоит диплом высшего и среднего образования и как его получить?
Купить диплом в России, предлагает наша компания
Всё, что нужно знать о покупке аттестата о среднем образовании
bvf.ru/forum/showthread.php?p=25261047#post25261047
Как оказалось, купить диплом кандидата наук не так уж и сложно
Процесс получения диплома стоматолога: реально ли это сделать быстро?
лечение запоев на дому http://www.motik13.0pk.me/viewtopic.php?id=2003 .
Как получить диплом техникума с упрощенным обучением в Москве официально
Реально ли приобрести диплом стоматолога? Основные шаги
Аттестат школы купить официально с упрощенным обучением в Москве
THA娛樂城
THA娛樂城與九州娛樂簡介
THA娛樂城是九州娛樂旗下的一個知名線上娛樂平台，致力於為玩家提供多元化且優質的娛樂服務。九州娛樂是亞洲地區領先的線上娛樂品牌，長期專注於打造穩定、公平且充滿樂趣的遊戲環境，旗下擁有多個知名娛樂平台，而THA娛樂城便是其中的一個旗艦產品。以下將詳細介紹THA娛樂城的特色與服務。
THA娛樂城的遊戲種類
THA娛樂城為玩家提供了多樣化的遊戲選擇，滿足不同玩家的需求與興趣，包括以下幾大類別：
1. 體育投注
體育迷可以在THA娛樂城享受豐富的體育賽事投注，涵蓋足球、籃球、網球等多項國際體育比賽。平台提供即時賠率和多種投注選項，讓玩家隨時掌握比賽動態並進行下注。
2. 真人娛樂
真人娛樂區提供即時互動的遊戲體驗，玩家可透過直播技術與真人荷官互動，遊玩如百家樂、輪盤、骰寶等經典遊戲。這不僅增添了真實感，更讓玩家有身臨其境的感受。
3. 電子老虎機
THA娛樂城匯集了多款高人氣的電子老虎機遊戲，從經典水果機到新潮主題機，皆配備精美的畫面與流暢的操作介面，為玩家帶來無限樂趣。
4. 捕魚遊戲
捕魚遊戲是許多玩家的最愛，THA娛樂城提供多種精美場景和豐富玩法的捕魚遊戲，玩家可以挑戰高額獎勵，享受射擊與策略結合的獨特樂趣。
5. 彩票與其他遊戲
除了以上幾類，平台還提供彩票遊戲及其他創新型娛樂遊戲，適合喜歡嘗試新鮮玩法的玩家。
九州娛樂的技術支持
作為THA娛樂城的母公司，九州娛樂以其強大的技術實力與嚴謹的管理體系為平台提供支持。九州娛樂採用國際領先的安全加密技術，確保玩家的個人資訊與交易數據得到妥善保護。此外，平台的遊戲結果皆經過嚴格的隨機性測試與第三方機構認證，保證公平公正。
優質的會員服務
THA娛樂城致力於打造一個高品質的會員體驗，其服務特色包括：
– 優惠活動
平台定期推出多種促銷活動，如新會員註冊禮金、存款返利、週週回饋等，讓玩家享受更多的遊戲資金。
– 快速出入金
平台提供便捷且快速的存提款服務，玩家可以安心進行資金操作，且無需擔心延遲問題。
– 24小時客戶服務
為了確保玩家的需求能即時被解決，THA娛樂城提供全年無休的客服支援，無論是遊戲問題還是技術諮詢，客服團隊都能快速回應。
與其他平台的區別
THA娛樂城之所以能在眾多線上娛樂平台中脫穎而出，不僅因其豐富的遊戲種類與高品質服務，更在於它所帶來的獨特價值：
1. 品牌信譽
作為九州娛樂旗下的品牌，THA娛樂城擁有長期積累的良好信譽，是許多玩家的首選。
2. 創新與多樣性
平台不斷推出新遊戲與創意玩法，讓玩家始終保持新鮮感。
3. 本地化服務
THA娛樂城深諳玩家需求，提供多語言支援與符合本地習慣的服務，提升玩家的使用便利性。
未來展望
隨著線上娛樂行業的快速發展，THA娛樂城也在持續進步與創新，力求為玩家帶來更多驚喜。無論是透過引進新的遊戲技術、擴展遊戲種類，還是改善服務品質，THA娛樂城都希望成為每位玩家的最佳娛樂夥伴。
總結來說，THA娛樂城憑藉其豐富的遊戲內容、可靠的技術支持以及優質的會員服務，已在亞洲娛樂市場佔有一席之地。如果您正在尋找一個結合刺激與信賴的娛樂平台，那麼THA娛樂城絕對值得一試。
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали сервисный центр apple в москве, можете посмотреть на сайте: сервисный центр apple
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
1c бухгалтерия цена 1c бухгалтерия цена .
вывод из запоя на дому похмельная https://www.domsadremont.ukrbb.net/viewtopic.php?f=3&t=907 .
st666 trang chủ
ST666 – Nền tảng sòng bạc trực tuyến hàng đầu tại Việt Nam
ST666 tự hào là một trong những thương hiệu uy tín hàng đầu trong lĩnh vực giải trí và sòng bạc trực tuyến tại châu Á. Với nhiều năm liên tục được bình chọn 5 sao, ST666 mang đến cho người chơi những trải nghiệm đẳng cấp và an toàn.
Lý do chọn ST666
Thương hiệu đáng tin cậy
ST666 là nền tảng được hàng triệu người chơi tại Việt Nam tin tưởng nhờ danh tiếng lâu năm và sự minh bạch trong hoạt động.
Sản phẩm đa dạng
Người chơi có thể tận hưởng hàng loạt trò chơi hấp dẫn như:
Nổ hũ: Đem lại cơ hội trúng thưởng lớn với đồ họa sống động.
Sòng bài: Bao gồm các trò chơi cổ điển như bài cào, baccarat, poker.
Thể thao: Đặt cược các trận đấu bóng đá, bóng rổ với tỷ lệ hấp dẫn.
Xổ số và bắn cá: Các trò chơi thú vị dành cho người yêu thích thử thách.
Đá gà: Một hình thức giải trí truyền thống được nâng cấp với chất lượng trực tuyến.
An ninh bảo mật
ST666 áp dụng công nghệ bảo mật tiên tiến, đảm bảo thông tin và giao dịch của người chơi luôn an toàn tuyệt đối.
Giao dịch nhanh chóng
Với hệ thống xử lý tự động hiện đại, ST666 cung cấp tốc độ nạp rút nhanh nhất, giúp người chơi tận hưởng trải nghiệm mượt mà.
Khuyến mãi hấp dẫn và dịch vụ chuyên nghiệp
ST666 không chỉ nổi bật với chất lượng sản phẩm mà còn thường xuyên tổ chức các chương trình khuyến mãi, tặng thưởng lớn. Đội ngũ hỗ trợ 24/7 luôn sẵn sàng giải đáp thắc mắc của khách hàng một cách tận tình.
Tin tức và mẹo chơi đá gà từ ST666
ST666 không ngừng cập nhật các bí quyết và thông tin mới nhất về đá gà, giúp người chơi nâng cao chiến lược và kỹ thuật. Từ việc chọn gà đá phù hợp đến cách chăm sóc và điều trị, mọi kiến thức đều được chia sẻ một cách chi tiết và chuyên nghiệp.
Tham gia ngay hôm nay!
Hãy truy cập ST666 – Trang chủ chính thức để trải nghiệm thế giới sòng bạc trực tuyến đa dạng và uy tín nhất. Không chỉ là nơi giải trí, ST666 còn mang đến cơ hội kiếm tiền hấp dẫn cho mọi người chơi.
Chơi ngay – Trải nghiệm đỉnh cao tại ST666!
Диплом вуза купить официально с упрощенным обучением в Москве
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Полезная информация как официально купить диплом о высшем образовании
Купить диплом ВУЗа России
Вопросы и ответы: можно ли быстро купить диплом старого образца?
일본배대지
메인 서비스: 간편하고 효율적인 배송 및 구매 대행 서비스
1. 대행 서비스 주요 기능
메인 서비스는 고객이 한 번에 필요한 대행 서비스를 신청할 수 있도록 다양한 기능을 제공합니다.
배송대행 신청: 국내외 상품 배송을 대신 처리하며, 효율적인 시스템으로 신속한 배송을 보장합니다.
구매대행 신청: 원하는 상품을 대신 구매해주는 서비스로, 고객의 수고를 줄입니다.
엑셀 대량 등록: 대량 상품을 엑셀로 손쉽게 등록 가능하여 상업 고객의 편의성을 증대합니다.
재고 관리 신청: 창고 보관 및 재고 관리를 통해 물류 과정을 최적화합니다.
2. 고객 지원 시스템
메인 서비스는 사용자 친화적인 접근성을 제공합니다.
유저 가이드: 대행 서비스를 더욱 합리적으로 사용할 수 있도록 세부 안내서를 제공합니다.
운송장 조회: 일본 사가와 등 주요 운송사의 추적 시스템과 연동하여 운송 상황을 실시간으로 확인 가능합니다.
3. 비용 안내와 부가 서비스
비용 계산기: 예상되는 비용을 간편하게 계산해 예산 관리를 돕습니다.
부가 서비스: 교환 및 반품, 폐기 및 검역 지원 등 추가적인 편의 서비스를 제공합니다.
출항 스케줄 확인: 해외 배송의 경우 출항 일정을 사전에 확인 가능하여 배송 계획을 세울 수 있습니다.
4. 공지사항
기본 검수 공지
무료 검수 서비스로 고객의 부담을 줄이며, 보다 철저한 검수가 필요한 경우 유료 정밀 검수 서비스를 권장합니다.
수출허가서 발급 안내
항공과 해운 수출 건에 대한 허가서를 효율적으로 발급받는 방법을 상세히 안내하며, 고객의 요청에 따라 이메일로 전달됩니다.
노데이터 처리 안내
운송장 번호 없는 주문에 대한 새로운 처리 방안을 도입하여, 노데이터 발생 시 관리비가 부과되지만 서비스 품질을 개선합니다.
5. 고객과의 소통
카카오톡 상담: 실시간 상담을 통해 고객의 궁금증을 해결합니다.
공지사항 알림: 서비스 이용 중 필수 정보를 지속적으로 업데이트합니다.
메인 서비스는 고객 만족을 최우선으로 하며, 지속적인 개선과 세심한 관리를 통해 최상의 경험을 제공합니다.
Как оказалось, купить диплом кандидата наук не так уж и сложно
Официальное получение диплома техникума с упрощенным обучением в Москве
Реально ли приобрести диплом стоматолога? Основные шаги
Стоимость дипломов высшего и среднего образования и процесс их получения
Как приобрести диплом о среднем образовании в Москве и других городах
Blackjack Jugabet Per? http://www.jugabet777.com/ .
вывод из запоя на дому екатеринбург tatuheart.ukrbb.net/viewtopic.php?f=8&t=15078 .
выведение из запоя врачом наркологом выведение из запоя врачом наркологом .
вывод из запоя на дому http://www.justforum.bestforums.org/viewtopic.php?f=26&t=4757 .
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
st666 trang chủ
ST666: Nhà Cái Đẳng Cấp Số 1 Việt Nam
Trong thế giới cá cược trực tuyến, ST666 đã khẳng định được cái tên của mình như một ngôi sao sáng tại thị trường Việt Nam. Với giao diện hiện đại và phong cách thiết kế trẻ trung, nhà cái này không chỉ là một sân chơi mà còn là một nơi để những người yêu thích cá cược có thể hòa mình vào những trải nghiệm thú vị và hấp dẫn nhất.
### Trải Nghiệm Cá Cược Đỉnh Cao
ST666 cung cấp rất nhiều loại hình cá cược từ chơi bài, đá gà, bắn cá đến thể thao và xổ số. Dù bạn là người mới bắt đầu hay là một cao thủ dày dạn kinh nghiệm, ST666 sẽ mang đến cho bạn những trò chơi đa dạng để thỏa mãn niềm đam mê của mình. Đặc biệt, nhờ vào việc đầu tư chăm chút từ giao diện trang chính cho đến từng sảnh cá cược, ST666 đưa người chơi vào một hành trình khám phá những điều kỳ diệu của cá cược trực tuyến.
### Hướng Dẫn Đăng Ký và Đăng Nhập
Việc đăng ký và đăng nhập tại ST666 rất đơn giản. Chỉ với vài bước dễ dàng, bạn đã có thể trở thành thành viên của một trong những nhà cái uy tín nhất. Hệ thống hỗ trợ trực tuyến 24/7 sẽ giúp bạn giải quyết mọi thắc mắc và vấn đề phát sinh khi tham gia cá cược.
### Chính Sách Bảo Mật và Đảm Bảo Quyền Lợi Người Chơi
ST666 luôn đặt sự an toàn và bảo mật của hội viên lên hàng đầu. Chính sách bảo mật nghiêm ngặt cùng với những điều khoản và điều kiện rõ ràng giúp người chơi hoàn toàn yên tâm khi tham gia cá cược tại đây. Thêm vào đó, nhà cái cũng cam kết minh bạch trong quá trình thanh toán và hỗ trợ tốt nhất cho người chơi.
### Khuyến Mãi Hấp Dẫn
Một trong những điểm mạnh của ST666 là hệ thống khuyến mãi đa dạng và hấp dẫn. Người chơi có thể tận dụng các ưu đãi để gia tăng cơ hội thắng lớn, cũng như nhận những phần quà giá trị hấp dẫn từ nhà cái.
### Liên Hệ và Hỗ Trợ
Nếu bạn cần thêm thông tin hoặc hỗ trợ, ST666 luôn sẵn sàng giúp đỡ. Có thể liên hệ trực tiếp theo địa chỉ và số điện thoại đã cung cấp, hoặc thông qua các kênh mạng xã hội như Facebook, Twitter, Pinterest, v.v.
### Kết Luận
ST666 không chỉ là một nhà cái, mà còn là một cộng đồng cá cược online năng động, nơi bạn có thể thỏa mãn đam mê và kiếm tiền dễ dàng. Với những nổi bật trong dịch vụ, thiết kế và chính sách bảo mật, ST666 chắc chắn sẽ là lựa chọn hàng đầu cho mọi tín đồ cá cược tại Việt Nam. Hãy tham gia ngay hôm nay để khám phá những trải nghiệm thú vị mà ST666 mang lại!
Полезные советы по безопасной покупке диплома о высшем образовании
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Аттестат 11 класса купить официально с упрощенным обучением в Москве
nhớ 666
Soi cầu bạc nhớ 666: Phương pháp cá cược lô đề chính xác và hiệu quả
Soi cầu bạc nhớ 666 là một trong những phương pháp soi cầu xổ số – lô đề cực kỳ hiệu quả và được nhiều cao thủ chơi cá cược áp dụng. Bởi vì, tỷ lệ trúng của phương pháp soi cầu này cao hơn so với nhiều phương pháp truyền thống khác.
ST666 sẽ cùng bạn khám phá về phương pháp soi cầu bạc nhớ 666, ưu điểm khi sử dụng soi cầu bạc nhớ trong cá cược lô đề, cách soi cầu bạc nhớ 666 đúng chuẩn năm 2024 ngay trong bài viết này.
Giới thiệu về soi cầu bạc nhớ 666
Soi cầu bạc nhớ 666 là một phương pháp phân tích kết quả xổ số dựa trên việc ghi nhớ và tổng hợp các con số đã từng xuất hiện trong quá khứ. Đây là một trong những công cụ cá cược nổi bật và được nhiều người chơi lựa chọn trong cộng đồng cá cược xổ số.
Những điểm nổi bật của soi cầu bạc nhớ 666:
Dựa vào dữ liệu thực tế: Thay vì dự đoán ngẫu nhiên, soi cầu bạc nhớ 666 sử dụng các con số từng xuất hiện và phân tích xác suất để đưa ra dự đoán kết quả xổ số sắp tới.
Thân thiện và dễ áp dụng: Phương pháp này không đòi hỏi người chơi phải có kiến thức sâu về thống kê. Chỉ cần hiểu cách ghi nhớ và phân tích cơ bản, người chơi có thể tự mình áp dụng phương pháp này.
Độ tin cậy cao: Nhờ vào dữ liệu lịch sử, soi cầu bạc nhớ 666 có khả năng dự đoán các con số có tỷ lệ lặp lại, giúp người chơi dự đoán chính xác hơn về các con số có thể xuất hiện.
Các phương pháp soi cầu bạc nhớ 666 đúng chuẩn năm 2024
Soi cầu bạc nhớ 666 là phương pháp dựa trên phân tích các kết quả xổ số từ trước đó để dự đoán các con số có khả năng xuất hiện tiếp theo.
Để nâng cao tỷ lệ thắng, bạn có thể áp dụng nhiều cách soi cầu bạc nhớ 666 khác nhau như soi cầu theo ngày, tuần, đầu câm, đuôi câm và theo thứ.
Soi cầu bạc nhớ 666 theo ngày
Soi cầu theo ngày là phương pháp phân tích các kết quả xổ số từ ngày hôm trước để dự đoán các con số có khả năng xuất hiện trong ngày tiếp theo.
Đây là phương pháp rất phù hợp với những người chơi muốn nhanh chóng nhận diện các xu hướng và tham gia cược ngay trong ngày.
Ví dụ:
Dữ liệu: Trong ngày hôm qua, các con số 05, 19, 26 xuất hiện khá nhiều.
Dự đoán: Bạn có thể thử các con số 06, 20, 27 trong ngày hôm nay vì chúng có khả năng liên quan đến các con số đã xuất hiện.
Soi cầu bạc nhớ 666 theo tuần
Soi cầu theo tuần giúp người chơi phân tích các kết quả của nhiều ngày trong tuần, từ đó nhận diện các chuỗi con số có khả năng tiếp tục xuất hiện trong các ngày tiếp theo. Phương pháp này hiệu quả trong việc nắm bắt xu hướng dài hạn hơn so với soi cầu theo ngày.
Ví dụ:
Dữ liệu: Trong tuần trước, các con số 02, 08, 18 xuất hiện vào các ngày thứ Hai và thứ Sáu.
Dự đoán: Tuần này, bạn có thể thử các con số 03, 09, 19 vào các ngày thứ Hai và thứ Sáu để tăng cơ hội thắng.
Soi cầu bạc nhớ 666 theo đầu câm
Đầu câm là các con số không xuất hiện ở vị trí đầu tiên trong kết quả xổ số. Dựa trên sự phân tích này, bạn có thể tìm ra những con số có khả năng xuất hiện tại đầu trong các lần quay số sau.
Ví dụ:
Dữ liệu: Trong các kỳ quay số gần đây, các con số 01, 02, 05 không xuất hiện ở vị trí đầu tiên.
Dự đoán: Bạn có thể thử các con số như 01, 02, 05 ở vị trí đầu trong các kỳ tiếp theo.
Soi cầu bạc nhớ theo đuôi câm
Đuôi câm là các con số không xuất hiện ở vị trí cuối cùng trong kết quả xổ số. Phân tích các con số này sẽ giúp bạn dự đoán những con số có khả năng xuất hiện ở đuôi trong lần quay tiếp theo.
Ví dụ:
Dữ liệu: Các con số 03, 09, 18 không xuất hiện ở vị trí cuối trong các kỳ quay gần đây.
Dự đoán: Bạn có thể thử các con số này ở vị trí cuối cùng trong các kỳ tiếp theo.
Soi cầu bạc nhớ 666 theo thứ
Быстрая покупка диплома старого образца: возможные риски
Всё, что нужно знать о покупке аттестата о среднем образовании без рисков
일본소비세환급
일본 소비세 환급, 네오리아와 함께라면 간편하고 안전하게
일본 소비세 환급은 복잡하고 까다로운 절차로 많은 구매대행 셀러들이 어려움을 겪는 분야입니다. 네오리아는 다년간의 경험과 전문성을 바탕으로 신뢰할 수 있는 서비스를 제공하며, 일본 소비세 환급 과정을 쉽고 효율적으로 처리합니다.
1. 일본 소비세 환급의 필요성과 네오리아의 역할
네오리아는 일본 현지 법인을 설립하지 않아도 합법적인 방식으로 소비세 환급을 받을 수 있는 솔루션을 제공합니다. 이를 통해:
한국 개인사업자와 법인 사업자 모두 간편하게 환급 절차를 진행할 수 있습니다.
일본의 복잡한 서류 심사를 최소화하고, 현지 로컬 세리사와 협력하여 최적의 결과를 보장합니다.
2. 소비세 환급의 주요 특징
일본 연고가 없어도 가능: 일본에 사업자가 없더라도 네오리아는 신뢰할 수 있는 서비스를 통해 소비세 환급을 지원합니다.
서류 작성 걱정 해결: 잘못된 서류 제출로 환급이 거절될까 걱정될 필요 없습니다. 네오리아의 전문 대응팀이 모든 과정을 정밀하게 관리합니다.
현지 법인 운영자를 위한 추가 지원: 일본 내 개인사업자나 법인 운영자에게는 세무 감사와 이슈 대응까지 포함된 고급 서비스를 제공합니다.
3. 네오리아 서비스의 장점
전문성과 신뢰성: 정부로부터 인정받은 투명성과 세무 분야의 우수한 성과를 자랑합니다.
맞춤형 서포트: 다양한 사례를 통해 쌓은 경험으로 고객이 예상치 못한 어려움까지 미리 해결합니다.
로컬 업체에서 불가능한 고급 서비스: 한국인 고객을 위해 정확하고 간편한 세무회계 및 소비세 환급 서비스를 제공합니다.
4. 네오리아가 제공하는 혜택
시간 절약: 복잡한 절차와 서류 준비 과정을 전문가가 대신 처리합니다.
안심 환급: 철저한 관리와 세심한 대응으로 안전하게 환급을 받을 수 있습니다.
추가 서비스: 세무감사와 이슈 발생 시 즉각적인 지원으로 사업의 연속성을 보장합니다.
네오리아는 소비세 환급이 복잡하고 어렵다고 느껴지는 고객들에게 최적의 길잡이가 되어드립니다. 신뢰를 바탕으로 한 전문적인 서비스로, 더 이상 소비세 환급 문제로 고민하지 마세요!
Купить диплом ВУЗа России
Официальное получение диплома техникума с упрощенным обучением в Москве
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
вывод из запоя цена https://odessaforum.0pk.me/viewtopic.php?id=10055 .
кухня заказ кухня заказ .
вывод из запоя цена http://www.motik13.0pk.me/viewtopic.php?id=2004/ .
Coolzino automaty online Coolzino automaty online .
Диплом вуза купить официально с упрощенным обучением в Москве
Как быстро получить диплом магистра? Легальные способы
windows1.listbb.ru/viewtopic.php?f=3&t=784
일본소비세환급
일본 소비세 환급, 네오리아와 함께라면 간편하고 안전하게
일본 소비세 환급은 복잡하고 까다로운 절차로 많은 구매대행 셀러들이 어려움을 겪는 분야입니다. 네오리아는 다년간의 경험과 전문성을 바탕으로 신뢰할 수 있는 서비스를 제공하며, 일본 소비세 환급 과정을 쉽고 효율적으로 처리합니다.
1. 일본 소비세 환급의 필요성과 네오리아의 역할
네오리아는 일본 현지 법인을 설립하지 않아도 합법적인 방식으로 소비세 환급을 받을 수 있는 솔루션을 제공합니다. 이를 통해:
한국 개인사업자와 법인 사업자 모두 간편하게 환급 절차를 진행할 수 있습니다.
일본의 복잡한 서류 심사를 최소화하고, 현지 로컬 세리사와 협력하여 최적의 결과를 보장합니다.
2. 소비세 환급의 주요 특징
일본 연고가 없어도 가능: 일본에 사업자가 없더라도 네오리아는 신뢰할 수 있는 서비스를 통해 소비세 환급을 지원합니다.
서류 작성 걱정 해결: 잘못된 서류 제출로 환급이 거절될까 걱정될 필요 없습니다. 네오리아의 전문 대응팀이 모든 과정을 정밀하게 관리합니다.
현지 법인 운영자를 위한 추가 지원: 일본 내 개인사업자나 법인 운영자에게는 세무 감사와 이슈 대응까지 포함된 고급 서비스를 제공합니다.
3. 네오리아 서비스의 장점
전문성과 신뢰성: 정부로부터 인정받은 투명성과 세무 분야의 우수한 성과를 자랑합니다.
맞춤형 서포트: 다양한 사례를 통해 쌓은 경험으로 고객이 예상치 못한 어려움까지 미리 해결합니다.
로컬 업체에서 불가능한 고급 서비스: 한국인 고객을 위해 정확하고 간편한 세무회계 및 소비세 환급 서비스를 제공합니다.
4. 네오리아가 제공하는 혜택
시간 절약: 복잡한 절차와 서류 준비 과정을 전문가가 대신 처리합니다.
안심 환급: 철저한 관리와 세심한 대응으로 안전하게 환급을 받을 수 있습니다.
추가 서비스: 세무감사와 이슈 발생 시 즉각적인 지원으로 사업의 연속성을 보장합니다.
네오리아는 소비세 환급이 복잡하고 어렵다고 느껴지는 고객들에게 최적의 길잡이가 되어드립니다. 신뢰를 바탕으로 한 전문적인 서비스로, 더 이상 소비세 환급 문제로 고민하지 마세요!
Стоимость дипломов высшего и среднего образования и процесс их получения
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
Купить диплом о среднем образовании в Москве и любом другом городе
Официальная покупка диплома вуза с упрощенной программой обучения
st666
ST666 | Đăng Nhập Nhà Cái ST666 Chính Thức Năm 2023
ST666 là điểm đến lý tưởng cho nhiều game thủ hiện nay, với vô số dịch vụ và sản phẩm hấp dẫn. Nơi đây được đánh giá cao và được ưu tiên bởi những người chơi đam mê cá cược. Hãy cùng tìm hiểu kỹ hơn về ST666 trong bài viết dưới đây.
ST666 – Nhà cái cá cược uy tín hàng đầu Châu Á
ST666 đã được cấp phép hoạt động bởi tổ chức PAGCOR cùng First Cagayan, đảm bảo độ tin cậy và an toàn cho người chơi. Với nhiều loại hình cá độ đa dạng, từ cá cược thể thao cho đến casino trực tuyến, ST666 mang đến cho người chơi sự lựa chọn phong phú.
Ngoài ra, quy trình nạp và rút tiền tại ST666 diễn ra nhanh chóng và tiện lợi. Người chơi có thể yên tâm tham gia mà không lo về vấn đề tài chính. Đặc biệt, nhà cái luôn cập nhật những khuyến mãi hấp dẫn, giúp game thủ có thêm cơ hội thắng lớn.
Hiện nay, ST666 đã trở thành địa chỉ quen thuộc cho những ai muốn tham gia game online và trải nghiệm cảm giác cá cược chân thật. Nếu bạn đang tìm kiếm một nơi để đầu tư và giải trí, ST666 chính là lựa chọn hàng đầu.
Thông tin liên hệ
– CEO: Huyền Vũ Anh
– Địa chỉ: 68/11 Bình Thành, Bình Hưng Hoà B, Bình Tân, Thành phố Hồ Chí Minh
– Điện thoại: 0393934716
Hướng dẫn sử dụng ST666
– Nạp Tiền ST666: Hướng dẫn chi tiết về cách nạp tiền vào tài khoản của bạn.
– Rút Tiền ST666: Quy trình rút tiền nhanh chóng và minh bạch.
– Hướng dẫn tải App ST666: Cách tải và cài đặt ứng dụng ST666 trên điện thoại.
– Đăng Ký Tài Khoản ST666: Các bước đơn giản để tạo tài khoản.
– Đăng Nhập Tài Khoản ST666: Hướng dẫn đăng nhập vào tài khoản cá cược.
– Đăng Ký Đại Lý ST666: Cơ hội hợp tác và trở thành đại lý của ST666.
Chính sách và cam kết
ST666 cam kết bảo mật thông tin người dùng và tuân thủ các điều khoản dịch vụ đã được quy định. Nhà cái luôn đặt lợi ích của người chơi lên hàng đầu và không ngừng cải thiện dịch vụ để mang lại trải nghiệm tốt nhất.
Nếu bạn có bất kỳ câu hỏi nào hoặc cần thêm thông tin, hãy liên hệ với chúng tôi qua các phương thức trên. Chúc bạn có những giây phút giải trí thú vị và may mắn tại ST666!
Summary of Cryptocurrency Transfer Check and Regulatory Solutions
In the current cryptocurrency market, guaranteeing transfer transparency and adherence with AML and Customer Identification rules is crucial. Below is an summary of leading platforms that provide tools for digital asset transaction monitoring, verification, and asset protection.
1. Tokenmetrics.com
Summary: Token Metrics provides cryptocurrency analysis to assess likely fraud threats. This service allows investors to examine tokens prior to buying to avoid possibly scam assets. Attributes:
– Threat evaluation.
– Ideal for investors looking to steer clear of questionable or fraud assets.
2. Metamask.Monitory.Center
Overview: Metamask.Monitory.Center allows individuals to verify their digital asset resources for suspicious transactions and standard compliance. Advantages:
– Verifies assets for legitimacy.
– Offers alerts about possible asset blockages on specific trading sites.
– Gives detailed results after address connection.
3. Bestchange.com
Description: Bestchange.ru is a site for observing and verifying crypto trade deals, providing transparency and deal safety. Benefits:
– Transaction and account observation.
– Compliance validation.
– Web-based portal; accommodates BTC and various additional cryptocurrencies.
4. Bot amlchek
Summary: AMLCheck Bot is a holding monitor and compliance tool that employs artificial intelligence models to detect dubious activity. Features:
– Deal observation and identity validation.
– Accessible via web version and Telegram.
– Compatible with digital assets including BSC, BTC, DOGE, and more.
5. Alfabit AML
Overview: AlfaBit delivers complete Anti-Money Laundering (AML) services specifically made for the crypto industry, helping firms and financial institutions in ensuring regulatory adherence. Features:
– Comprehensive anti-money laundering options and screenings.
– Meets modern protection and regulatory requirements.
6. Node AML
Summary: AML Node delivers AML and KYC services for crypto businesses, such as transaction tracking, sanctions screening, and risk assessment. Highlights:
– Risk evaluation tools and compliance screenings.
– Valuable for maintaining secure firm activities.
7. Btrace.AMLcrypto.io
Summary: Btrace.AMLcrypto.io specializes in asset verification, offering transaction observation, sanctions checks, and assistance if you are a victim of theft. Benefits:
– Reliable help for fund restoration.
– Deal tracking and protection features.
Exclusive USDT Check Services
Our website also reviews multiple sites providing check solutions for crypto transfers and holdings:
– **USDT TRC20 and ERC20 Validation:** Various sites support detailed evaluations for USDT deals, aiding in the detection of doubtful transactions.
– **AML Screening for USDT:** Tools are available for monitoring for fraudulent activities.
– **“Cleanliness” Validation for Holdings:** Validation of transfer and wallet “cleanliness” is available to identify possible risks.
**Summary**
Choosing the suitable platform for validating and monitoring cryptocurrency transfers is important for providing safety and regulatory compliance. By reading our reviews, you can select the best tool for transfer observation and resource protection.
ST666.LOVE – Nhà cái uy tín và nền tảng cá cược hàng đầu tại Việt Nam
ST666 là một thương hiệu cá cược nổi bật tại Việt Nam, mang đến trải nghiệm giải trí toàn diện và an toàn cho người chơi. Với hàng loạt tính năng hiện đại, chương trình khuyến mãi hấp dẫn, và dịch vụ chăm sóc khách hàng tận tâm, ST666 xứng đáng là lựa chọn số một của bạn trong thế giới cá cược trực tuyến.
Thông báo quan trọng về link đăng nhập ST666
Để đảm bảo an toàn và tránh các trường hợp gián đoạn truy cập, link đăng nhập vào ST666 có thể thay đổi liên tục. Trước khi nạp tiền, quý khách vui lòng liên hệ với nhân viên hỗ trợ để nhận thông tin mới nhất. Chúng tôi cam kết đồng hành cùng bạn, mang đến trải nghiệm cá cược may mắn và thuận lợi.
Các tính năng nổi bật của ST666
Hệ thống sảnh chơi đa dạng
Casino: Đắm mình trong không gian sòng bài trực tuyến sang trọng.
Thể thao: Đặt cược với tỷ lệ hấp dẫn trong các trận đấu thể thao hàng đầu.
Đá gà: Trực tiếp từ đấu trường SV388 với chất lượng video sắc nét.
Slot quay, bắn cá, xổ số, eSport: Phong phú lựa chọn, thỏa sức trải nghiệm.
Khuyến mãi hấp dẫn
Thưởng 100% nạp đầu: Tăng gấp đôi cơ hội chiến thắng.
Hoàn tiền 10% mỗi ngày: An tâm chơi không lo rủi ro.
Thưởng nóng: Nhận ngay 100K cho thành viên mới.
Ứng dụng ST666 tiện lợi
Tải app ST666 trên các nền tảng iOS và Android, giúp bạn truy cập dễ dàng, mọi lúc mọi nơi.
An toàn và minh bạch
ST666 được cấp chứng chỉ hoạt động hợp pháp, cam kết mang đến môi trường cá cược uy tín, bảo mật cao.
Hướng dẫn tham gia ST666
Đăng ký tài khoản: Nhanh chóng qua giao diện thân thiện của website hoặc ứng dụng.
Đăng nhập và nạp tiền: Sử dụng nhiều phương thức thanh toán tiện lợi.
Rút tiền dễ dàng: Hệ thống xử lý giao dịch tự động, đảm bảo tốc độ nhanh chóng.
Trải nghiệm đẳng cấp tại ST666.LOVE
ST666 không chỉ là nền tảng giải trí mà còn là nơi hội tụ của những trò chơi cá cược đỉnh cao. Hãy tham gia ngay hôm nay để nhận nhiều ưu đãi hấp dẫn và trải nghiệm những phút giây sôi động.
Liên hệ ST666 để được hỗ trợ và nhận link đăng nhập mới nhất. Chúc quý khách may mắn!
Сколько стоит диплом высшего и среднего образования и как его получить?
Легальные способы покупки диплома о среднем полном образовании
Сколько стоит получить диплом высшего и среднего образования легально?
частный нарколог на дом http://www.ya.7bb.ru/viewtopic.php?id=14616#p41014 .
платный нарколог на дом https://www.severussnape.borda.ru/?1-4-0-00000319-000-0-0-1730786111 .
выведение из запоя в сочи http://familyportal.forumrom.com/viewtopic.php?id=28581 .
вывод из запоя на дому в сочи https://svarog.forum24.ru/?1-0-0-00000227-000-0-0-1730787062 .
стационарное выведение из запоя https://pelsh.forum24.ru/?1-8-0-00000128-000-0-0-1730786505/ .
פיתוח אתרים
九州娛樂城：亞洲頂級線上娛樂平台
九州娛樂城，作為亞洲領先的線上博弈平台，以其專業性、公平性和創新性著稱。在這裡，您可以享受全方位的娛樂體驗，包括體育投注、真人遊戲、電子遊戲、六合彩球以及流行的捕魚機和棋牌遊戲。九州娛樂城是台灣玩家的首選娛樂平台，被譽為業界 No.1！
九州娛樂城的亮點
1. 多元化遊戲選擇
九州娛樂城擁有超過千款來自全球頂尖供應商提供的遊戲，滿足各種類型玩家的需求。無論是喜歡競技性的體育投注、刺激的真人遊戲，還是休閒的電子遊戲，九州娛樂城都能提供最適合您的選擇。
體育投注：全面覆蓋世界級賽事，包括世界杯、職業聯賽等。提供多種投注方式，如讓球、大小、單雙、串關等，並支持桌面端與手機端投注。
真人遊戲：KU真人百家樂、LEO真人遊戲等，讓您感受現場賭桌的真實刺激。
電子遊戲與捕魚機：多款熱門遊戲，如九州熱門電子遊戲和捕魚機，帶給玩家極致娛樂享受。
六合彩與棋牌遊戲：適合策略型玩家的理想選擇。
2. 極致便利的操作體驗
九州娛樂城支持通過官方網站和九州APP下載進行操作，無論您身在何處，都可以輕鬆加入遊戲世界。針對台灣玩家的本地化設計確保操作流暢、存取款方便。
3. 先進技術與安全保障
九州娛樂城集團總部位於菲律賓首都馬尼拉的RCBC Plaza，配備世界一流的安全資訊防護系統和智能大樓自動化系統（BAS）。玩家的數據與資金安全都能得到最佳保障，讓每一次遊戲都安心無憂。
4. 熱門品牌與平台支持
九州娛樂城旗下包括三大品牌：
LEO娛樂：提供真人遊戲、體育直播及免費影城。
THA娛樂：專注於新手友好和便捷操作。
KU娛樂：以真人百家樂而著稱。
每個品牌雖分別由不同管理團隊運營，但都傳承了九州娛樂城的高標準，遊戲系統與界面毫無差異，為玩家提供無縫娛樂體驗。
為什麼選擇九州娛樂城？
專業性與公平性
九州娛樂城堅持以「即時便利、公平公正、專業營運」為宗旨，研發創新遊戲技術，滿足不同類型玩家需求。
貼近市場與玩家需求
擁有兩岸三地的精英設計師與代理團隊，根據玩家反饋持續改進產品，並為合作商提供及時更新支持。
優越的服務與保障
從遊戲操作到客戶支持，九州娛樂城提供全面的服務支持，讓每位玩家都能感受到最貼心的服務。
九州娛樂城的未來
作為線上博弈行業的領航者，九州娛樂城不斷推陳出新，致力於提供更豐富的遊戲選擇和更完善的玩家體驗。同時，透過強大的技術與營運團隊，九州娛樂城已成為台灣乃至亞洲地區娛樂平台的代名詞。
立即下載九州APP，體驗最極致的娛樂樂趣！九州娛樂城——您的最佳線上娛樂夥伴！
Рекомендации по безопасной покупке диплома о высшем образовании
Как получить диплом техникума официально и без лишних проблем
вывод из запоя сочи вывод из запоя сочи .
выведение из запоя в сочи выведение из запоя в сочи .
вывод из запоя стационар вывод из запоя стационар .
вывод из запоя стационар вывод из запоя стационар .
вывод из запоя в стационаре вывод из запоя в стационаре .
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали сервисный центр asus рядом, можете посмотреть на сайте: сервисный центр asus цены
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
ST666: Thiên Đường Casino Trực Tuyến Hàng Đầu
ST666 là một trong những sòng bạc trực tuyến hàng đầu, mang đến trải nghiệm chơi game đỉnh cao với hàng loạt trò chơi hấp dẫn và chương trình khuyến mãi đặc biệt. Với sứ mệnh đem lại sân chơi công bằng và tiện lợi, ST666 đã trở thành lựa chọn yêu thích của hàng ngàn người chơi tại Việt Nam.
Đa Dạng Trò Chơi và Sảnh Cược
1. Trò Chơi Phong Phú
ST666 cung cấp nhiều trò chơi đa dạng, đáp ứng sở thích của mọi người chơi:
Baccarat: Trò chơi cổ điển dành cho những ai yêu thích chiến thuật và may mắn.
Tài Xỉu: Trò chơi xúc xắc đầy kịch tính, đem lại cơ hội thắng lớn trong từng vòng cược.
Xóc Đĩa: Trò chơi truyền thống Việt Nam, được nâng cấp với công nghệ trực tuyến hiện đại.
Và nhiều trò chơi khác đang chờ bạn khám phá.
2. Sảnh Cược Đẳng Cấp
ST666 kết hợp cùng các sảnh cược nổi tiếng như:
Wm Casino: Nền tảng casino chuyên nghiệp, nổi bật với các trò chơi chất lượng cao và giao diện mượt mà.
ST666 Casino: Sảnh cược độc quyền với những ưu đãi hấp dẫn và các trò chơi độc đáo.
Khuyến Mãi Hấp Dẫn Tại ST666
ST666 không chỉ nổi bật với danh mục trò chơi phong phú mà còn mang đến nhiều chương trình khuyến mãi hấp dẫn cho người chơi:
Khuyến Mãi Gửi Tiền Cuối Tuần: Nhận thưởng lên đến 3.666.000 đồng khi nạp tiền vào tài khoản trong các ngày cuối tuần.
Ưu Đãi Đặc Biệt Dành Cho Hội Viên Mới: Những người chơi mới sẽ nhận được gói khuyến mãi chào mừng độc quyền.
Hoàn Tiền Hàng Tuần: Cơ hội nhận lại phần trăm số tiền cược đã thua trong tuần, giúp bạn có thêm động lực tham gia.
Tại Sao Nên Chọn ST666?
An Toàn và Uy Tín: ST666 cam kết bảo mật thông tin và giao dịch của người chơi, đảm bảo trải nghiệm chơi game an toàn tuyệt đối.
Hỗ Trợ Khách Hàng Chuyên Nghiệp: Đội ngũ chăm sóc khách hàng luôn sẵn sàng hỗ trợ 24/7.
Giao Diện Thân Thiện: Thiết kế đơn giản, dễ sử dụng, phù hợp cho cả người mới chơi và người chơi lâu năm.
Cơ Hội Thắng Lớn: Tỷ lệ thắng cao và phần thưởng hấp dẫn trong từng trò chơi.
Cách Tham Gia ST666
Bước 1: Truy cập trang web chính thức của ST666.
Bước 2: Đăng ký tài khoản nhanh chóng và miễn phí.
Bước 3: Nạp tiền và lựa chọn trò chơi yêu thích để bắt đầu hành trình giải trí.
Kết Luận
ST666 chính là thiên đường giải trí trực tuyến dành cho những ai yêu thích thử vận may và tận hưởng các trò chơi đẳng cấp. Với sự kết hợp giữa công nghệ hiện đại và các chương trình ưu đãi hấp dẫn, ST666 cam kết mang lại trải nghiệm hoàn hảo cho người chơi. Tham gia ngay hôm nay để khám phá những điều bất ngờ tại ST666!
ST666 – Nhận Định Bóng Đá Kèo Nhà Cái Uy Tín
ST666: Địa Chỉ Lý Tưởng Cho Những Tín Đồ Cá Cược Bóng Đá
ST666 là nền tảng nhận định bóng đá và kèo nhà cái chuyên nghiệp, nơi người chơi có thể tham gia dự đoán các kèo đa dạng như cược tài xỉu, cược chấp, và cược 1×2. Với giao diện thân thiện, tỷ lệ cược minh bạch và ưu đãi hấp dẫn, ST666 đang dần trở thành lựa chọn hàng đầu của cộng đồng yêu bóng đá.
Nhận Định Kèo Nhà Cái Đa Dạng
Cược Tài Xỉu (#cuoctaixiu)
Dựa vào tổng số bàn thắng trong trận đấu, người chơi dễ dàng chọn lựa Tài (nhiều hơn tỷ lệ nhà cái đưa ra) hoặc Xỉu (ít hơn tỷ lệ).
ST666 cung cấp các phân tích chi tiết giúp người chơi đưa ra lựa chọn chính xác.
Cược Chấp (#cuocchap)
Thích hợp cho những trận đấu có sự chênh lệch về sức mạnh giữa hai đội. ST666 cung cấp tỷ lệ chấp tối ưu, phù hợp với cả người chơi mới và chuyên nghiệp.
Cược 1×2 (#cuoc1x2)
Phù hợp cho những ai muốn dự đoán kết quả chung cuộc (Thắng – Hòa – Thua). Đây là loại kèo phổ biến, dễ hiểu và có tỷ lệ cược hấp dẫn.
Ưu Đãi Hấp Dẫn Tại ST666
Nhận 160% tiền gửi lần đầu: Khi đăng ký tài khoản mới và nạp tiền, người chơi sẽ nhận được số tiền thưởng cực lớn, tăng cơ hội tham gia các kèo.
Hoàn tiền 3% mỗi ngày: Chính sách hoàn tiền giúp người chơi giảm thiểu rủi ro, thoải mái trải nghiệm mà không lo lắng nhiều về chi phí.
Vì Sao Nên Chọn ST666?
Nền Tảng Uy Tín: ST666 cam kết mang đến trải nghiệm cá cược minh bạch và an toàn.
Phân Tích Chuyên Sâu: Đội ngũ chuyên gia của ST666 luôn cập nhật nhận định mới nhất về các trận đấu, giúp người chơi đưa ra quyết định tối ưu.
Hỗ Trợ 24/7: Đội ngũ hỗ trợ chuyên nghiệp, luôn sẵn sàng giải đáp thắc mắc của người chơi.
Giao Dịch Nhanh Chóng: Nạp rút tiền linh hoạt, đảm bảo sự tiện lợi và bảo mật.
Cách Tham Gia ST666
Truy cập website chính thức của ST666.
Đăng ký tài khoản bằng thông tin cá nhân.
Nạp tiền lần đầu để nhận ưu đãi 160%.
Bắt đầu trải nghiệm cá cược với các kèo yêu thích!
Hãy đến với ST666 để tận hưởng không gian cá cược chuyên nghiệp, nhận định kèo chất lượng và những phần thưởng hấp dẫn. Tham gia ngay hôm nay để trở thành người chơi chiến thắng!
leo娛樂城登入
LEO娛樂城：九州娛樂集團的卓越創舉與運營優勢
九州娛樂集團總部的現代化運營
九州娛樂集團的總部設於菲律賓首都馬尼拉市中心最具代表性的現代化建築「RCBC Plaza」。這座辦公大樓融合了全球領先的建築科技與安全系統，包括：
國家級資訊防護系統，確保數據安全。
樓宇自動化系統 (BAS)，實現數位化管理與高效運營，包括防火系統、光纖電訊和數位監控。
九州娛樂為員工提供舒適的工作環境和專業的教育培訓，確保服務水準一流。其員工以專業知識和親切態度，為尊貴玩家帶來極致的遊戲體驗。
LEO娛樂旗下品牌與遊戲特色
九州娛樂城旗下分支包括 LEO、THA 和 KU 三個娛樂品牌。雖然品牌各自獨立運營，但都共享相同的遊戲系統與界面，提供超過數千款來自全球頂級供應商的遊戲。
這些品牌的核心特色包括：
種類繁多的遊戲：滿足不同類型玩家的需求，包括電子遊戲、體育博彩、真人娛樂等。
不斷更新的內容：通過九州獨家技術，網站內容保持新鮮，合作商可快速更新遊戲資源，確保平台競爭力。
玩家在這些平台上可以隨時找到適合自己的遊戲，享受沉浸式的娛樂體驗。
LEO娛樂城的歷史與發展
九州娛樂集團的起源可以追溯至其最早期的經營模式：「信用版」賭博平台 《天下體育球版》。儘管該模式在當時非常流行，但因高風險與財務處理複雜而逐漸被淘汰。
隨著市場需求的變化，九州娛樂轉型為現金版平台 《天下現金網》，引入了更安全、便捷的遊戲模式。這種轉變不僅提升了玩家的體驗，也使平台得以進一步發展。
如今，九州娛樂城已成為台灣博弈業界的領軍者，不僅優化了網站版面與功能，還推出了專屬手機APP，方便玩家隨時隨地進行遊戲體驗。
LEO娛樂的成功秘訣
現代化運營與技術支持：九州娛樂在系統安全與技術更新方面投入巨大資源，確保平台運營穩定可靠。
多元化遊戲體驗：通過與全球頂級遊戲供應商合作，平台提供了豐富的遊戲選擇，適應各種玩家需求。
用戶至上：專業培訓的員工以細心和熱忱態度，提供高品質服務，讓玩家倍感尊重。
不斷創新：從信用版到現金版，再到手機APP，九州娛樂始終緊跟市場趨勢，致力於打造最佳娛樂體驗。
結語
LEO娛樂城作為九州娛樂集團旗下的重要品牌，不僅繼承了集團的核心價值，更在遊戲選擇、服務品質和技術創新方面不斷提升。從最初的《天下體育球版》到如今的行業領先者，LEO娛樂見證了九州娛樂城的發展歷程，也成為博弈行業中的耀眼明星。
加入 LEO娛樂城，感受來自九州娛樂集團的專業與熱情，享受最頂級的線上博弈體驗！
ST666 Xổ Số – Điểm Đến Giải Trí Hoàn Hảo
ST666 Xổ Số là nền tảng giải trí trực tuyến hàng đầu, cung cấp đa dạng các loại hình trò chơi từ keno, xổ số miền Nam (XSMN), xổ số miền Bắc (XSMB) đến xổ số siêu tốc. Với dịch vụ chuyên nghiệp và an toàn, ST666 mang đến cho bạn một trải nghiệm hoàn toàn mới mẻ và hấp dẫn.
Tại Sao Nên Chọn ST666 Xổ Số
Truy Cập Nhanh Và An Toàn
ST666 đảm bảo quyền truy cập nhanh chóng thông qua đường dẫn chính thức, loại bỏ hoàn toàn rủi ro từ các trang web giả mạo hoặc nguy cơ mất tài khoản. Hệ thống bảo mật hiện đại giúp bạn yên tâm khi đăng nhập và tham gia trò chơi.
Ưu Đãi Độc Quyền Dành Cho Thành Viên
ST666 mang đến nhiều chương trình khuyến mãi đặc biệt dành riêng cho người chơi, bao gồm phần thưởng giá trị và các ưu đãi hấp dẫn. Thành viên mới sẽ được trải nghiệm các chính sách hỗ trợ vượt trội, giúp tăng cơ hội chiến thắng và tận hưởng trò chơi tốt nhất.
Bảo Mật Thông Tin Tối Đa
Hệ thống mã hóa hiện đại của ST666 đảm bảo mọi giao dịch và dữ liệu cá nhân đều được bảo vệ an toàn. Mọi thông tin đều được xử lý theo quy chuẩn bảo mật cao nhất, giúp người chơi yên tâm giải trí mà không lo lắng về vấn đề rủi ro thông tin.
Đa Dạng Trò Chơi Giải Trí
Xổ số: Từ xổ số truyền thống như XSMN, XSMB đến xổ số siêu tốc, đáp ứng mọi nhu cầu giải trí của người chơi.
Lô đề: Cung cấp giao diện dễ sử dụng, giúp bạn dễ dàng chọn số và theo dõi kết quả trực tiếp.
Casino trực tuyến: Đa dạng các trò chơi từ bài bạc, roulette đến các game đổi thưởng hiện đại.
Những Lợi Ích Khi Chơi Tại ST666
Dịch vụ hỗ trợ khách hàng chuyên nghiệp hoạt động 24/7.
Giao dịch nạp và rút tiền nhanh chóng, minh bạch.
Hệ thống cập nhật trò chơi thường xuyên, mang lại sự mới mẻ và không nhàm chán.
Nền tảng thiết kế hiện đại, thân thiện với mọi thiết bị, từ máy tính đến điện thoại di động.
Cách Truy Cập ST666
Truy cập đường dẫn chính thức của ST666 để đảm bảo an toàn.
Đăng ký tài khoản và hoàn tất các bước xác thực thông tin.
Tham gia các trò chơi hấp dẫn và tận hưởng phần thưởng đặc biệt dành cho thành viên.
ST666 Xổ Số không chỉ là nền tảng giải trí mà còn là nơi mang lại cơ hội chiến thắng và trải nghiệm dịch vụ đẳng cấp. Tham gia ngay hôm nay để khám phá một thế giới giải trí đa dạng và chuyên nghiệp!
娛樂城
RG富遊娛樂城：台灣線上娛樂城的最佳選擇
RG富遊娛樂城以其卓越的服務和多樣化的遊戲選擇，成為2024年最受歡迎的線上娛樂平台。受到超過50位網紅和部落客的實測推薦，這座娛樂城不僅提供豐富的遊戲，還帶來眾多優惠活動和誠信保證，贏得了廣大玩家的信任與青睞。
RG富遊娛樂城的獨特優勢
多重優惠活動
體驗金 $168：新手玩家可以免費試玩，無需任何成本即可體驗高品質遊戲。
首儲1000送1000：首次存款即可獲得雙倍金額，增加遊戲的樂趣與機會。
線上簽到轉盤：每日簽到即可參加抽獎，贏取現金獎勵和豐厚禮品。
快速存提款與資金保障
RG富遊採用自主研發的財務系統，確保5秒快速存款，滿足玩家即時遊戲需求。
100%保證出金，杜絕任何拖延或資金安全風險，讓玩家完全放心。
遊戲種類豐富
RG富遊娛樂城涵蓋多種遊戲類型，滿足不同玩家的需求，包括：
真人百家樂：與真人荷官互動，感受真實賭場的刺激氛圍。
電子老虎機：超過數百款創新遊戲，玩法新穎，回報豐厚。
電子捕魚：趣味性強，結合策略與娛樂，深受玩家喜愛。
電子棋牌：提供公平競技環境，適合策略型玩家。
體育投注：涵蓋全球賽事，賠率即時更新，為體育愛好者提供最佳選擇。
樂透彩票：參與多地彩票，挑戰巨額獎金。
跨平台兼容性
RG富遊支持Web端、H5、iOS和Android設備，玩家可隨時隨地登錄遊戲，享受無縫體驗。
與其他娛樂城的不同之處
RG富遊以現金版模式運營，確保交易透明和安全性。相比一般娛樂城，RG富遊在存提款速度上遙遙領先，玩家可在短短15秒內完成交易，並且100%保證資金提領。而在線客服全年無休，隨時提供支持，讓玩家在任何時間都能解決問題。
相比之下，一般娛樂城多以信用版模式運營，存在出金風險，且存提款速度較慢，客服服務不穩定，無法與RG富遊的專業性相比。
為什麼選擇RG富遊娛樂城
資金交易安全無憂：採用最先進的SSL加密技術，確保每筆交易的安全性。
遊戲種類全面豐富：每日更新多樣化遊戲，帶來新鮮感和無限可能。
優惠活動力度大：從體驗金到豐厚的首儲獎勵，玩家每一步都能享受優惠。
快速存提款服務：自主研發技術保障流暢交易，遊戲不中斷。
全天候專業客服：24/7在線支持，及時解決玩家需求。
立即加入RG富遊娛樂城
RG富遊娛樂城不僅提供豐富的遊戲體驗，更以專業的服務、完善的安全保障和多樣的優惠活動，為玩家打造一個值得信賴的娛樂環境。立即註冊，體驗台灣最受歡迎的線上娛樂城！
Быстрое обучение и получение диплома магистра – возможно ли это?
вывод из запоя на дому сочи вывод из запоя на дому сочи .
капельница от запоя в сочи капельница от запоя в сочи .
вывод из запоя в стационаре вывод из запоя в стационаре .
car rental wien
Официальная покупка диплома вуза с сокращенной программой в Москве
Купить диплом старого образца, можно ли это сделать по быстрой схеме?
شراء جميع أنواع الأثاث الميستعمل بالرياض
شراء الأثاث المستعمل بالرياض: الحل الأمثل للتخلص من الأثاث القديم واستبداله
هل تبحث عن وسيلة للاستفادة من أثاثك القديم بدلاً من تخزينه أو التخلص منه؟ تقدم محلات شراء وبيع الأثاث المستعمل بالرياض حلاً مثالياً يساعد الأفراد والمؤسسات على تحقيق أقصى استفادة من الأثاث القديم. نحن نعمل كحلقة وصل بين من يرغبون في بيع أثاثهم المستعمل ومن يبحثون عن قطع مميزة تلبي احتياجاتهم.
لماذا تختار شركتنا لشراء الأثاث المستعمل بالرياض؟
أفضل العروض وأعلى معدلات التسعير
نحن نقدم تقييمًا دقيقًا ومنصفًا لأثاثك المستعمل بناءً على خبرة فريقنا من الخبراء.
خدمات تغطي منطقة الرياض بالكامل
بمجرد اتصالك بنا، نصل إليك بسرعة أينما كنت داخل الرياض.
تقييم احترافي للأثاث
يتم تثمين الأثاث بناءً على آراء مجموعة محايدة من الخبراء لضمان الشفافية والدقة.
تغيير الديكور بسهولة
إذا كنت تخطط للانتقال إلى منزل جديد أو ترغب في تحديث الديكور الخاص بك، فإن بيع الأثاث القديم واستبداله بأثاث جديد يُعتبر خطوة عملية وفعالة.
عوامل تؤثر على قرار بيع أو الاحتفاظ بالأثاث القديم
القيمة العملية للأثاث
إذا كانت القطعة القديمة تناسب احتياجاتك وتنسجم مع الديكور الجديد، قد ترغب في الاحتفاظ بها. أما القطع المتضررة أو غير المريحة، فبيعها هو الخيار الأفضل.
جودة الأثاث
نقل أثاث على وشك الانهيار إلى منزلك الجديد قد يسبب خسائر مادية ويستهلك جهدًا بلا جدوى.
حجم الأثاث ومدى ملاءمته للمساحة
تأكد من قياس المساحات المتوفرة في المنزل الجديد وتوافقها مع حجم الأثاث القديم قبل اتخاذ قرار الاحتفاظ به.
القيمة العاطفية
بعض القطع تحمل قيمة عاطفية تجعل التخلي عنها صعبًا. إذا كان بالإمكان نقلها بأمان، يمكنك الاحتفاظ بها.
خطر التلف أثناء النقل
إذا كان الأثاث معرضًا للتلف الكبير أثناء النقل، فمن الأفضل التفكير في بيعه لتجنب خسائر محتملة.
خدماتنا المميزة لشراء وبيع الأثاث المستعمل بالرياض
شراء جميع أنواع الأثاث: غرف نوم، مجالس، أثاث الفلل والقصور، وأجهزة كهربائية.
تقييم دقيق وسعر عادل: نضمن تقديم السعر الحقيقي لأثاثك بناءً على حالته.
شراء المكيفات المستعملة بالرياض: نحن الأفضل في هذا المجال، مع فريق متخصص يقدم حلولاً تناسب احتياجاتك.
لماذا نحن الأفضل؟
لدينا فريق من الخبراء في تقييم وشراء الأثاث المستعمل.
نقدم خدمات تغطي جميع مناطق الرياض.
نعمل على بناء ثقة العملاء من خلال الشفافية والالتزام.
اتصل بنا الآن
إذا كنت تبحث عن أفضل محلات شراء الأثاث المستعمل بالرياض، فلا تتردد في التواصل معنا عبر الجوال أو الواتساب على الرقم 0500220488. نحن مستعدون لخدمتك أينما كنت وفي أي وقت يناسبك. اجعل بيع أثاثك القديم خطوة سهلة ومربحة معنا!
Легальная покупка диплома о среднем образовании в Москве и регионах
crypto address checker
Overview of Cryptocurrency Transfer Validation and Compliance Options
In today’s crypto market, ensuring transaction transparency and conformity with AML and Customer Identification rules is vital. Here is an summary of leading platforms that offer solutions for cryptocurrency transfer tracking, check, and resource protection.
1. Token Metrics Platform
Overview: Tokenmetrics delivers crypto analysis to evaluate likely fraud threats. This service enables users to check cryptocurrencies prior to investment to avoid likely fraudulent holdings. Features:
– Danger analysis.
– Suitable for holders aiming to steer clear of questionable or fraudulent assets.
2. Metamask.Monitory.Center
Summary: Metamask.Monitory.Center permits users to review their cryptocurrency holdings for doubtful actions and compliance compliance. Advantages:
– Checks tokens for legitimacy.
– Provides warnings about possible resource blockages on specific platforms.
– Gives thorough results after wallet connection.
3. Best Change
Overview: Best Change is a site for tracking and validating crypto exchange deals, providing openness and transaction safety. Features:
– Transfer and wallet tracking.
– Restriction screening.
– Internet portal; supports BTC and various other coins.
4. AML Bot
Description: AMLCheck Bot is a portfolio observer and AML service that employs machine learning methods to identify dubious actions. Highlights:
– Transaction tracking and personal validation.
– Available via internet and Telegram.
– Supports cryptocurrencies such as BSC, BTC, DOGE, and other types.
5. AlfaBit
Overview: AlphaBit provides thorough Anti-Money Laundering (AML) solutions customized for the crypto industry, assisting businesses and banks in maintaining regulatory compliance. Features:
– Thorough anti-money laundering features and evaluations.
– Meets modern security and regulatory guidelines.
6. Node AML
Summary: AMLNode delivers compliance and identification tools for digital currency businesses, such as deal tracking, sanctions screening, and evaluation. Highlights:
– Threat assessment tools and sanctions screenings.
– Useful for ensuring protected firm processes.
7. Btrace.AMLcrypto.io
Summary: Btrace.AMLcrypto.io focuses on fund validation, delivering transaction tracking, restriction screenings, and assistance if you are a target of fraud. Highlights:
– Effective help for resource restoration.
– Transfer monitoring and protection options.
Specialized USDT Check Options
Our site also reviews different platforms that offer verification solutions for crypto transfers and wallets:
– **USDT TRC20 and ERC20 Verification:** Many services provide detailed evaluations for USDT transactions, helping in the identification of doubtful actions.
– **AML Screening for USDT:** Options are available for monitoring for money laundering actions.
– **“Cleanliness” Checks for Accounts:** Checking of transaction and holding “cleanliness” is available to find possible risks.
**Conclusion**
Finding the best platform for verifying and monitoring crypto transfers is essential for guaranteeing protection and regulatory adherence. By consulting our recommendations, you can select the most suitable service for transaction tracking and fund security.
Быстрая схема покупки диплома старого образца: что важно знать?
Аттестат 11 класса купить официально с упрощенным обучением в Москве
Полезные советы по безопасной покупке диплома о высшем образовании
Легальная покупка диплома о среднем образовании в Москве и регионах
testforumrp.forumex.ru/viewtopic.php?f=7&t=135
Jugabet apuestas Jugabet apuestas .
Сколько стоит получить диплом высшего и среднего образования легально?
Betovo live casin? Betovo live casin? .
Купить диплом Барнаул
Казино Казино .
казино молдов казино молдов .
вывод из запоя стационар вывод из запоя стационар .
eriacta salt – zenegra grass forzest exchange
DOOH media monitoring in Nigeria
Retinaad Limited represents the most prominent advertising technology company for campaign oversight & viewership tracking within the Nigerian market.
We deliver evaluation, monitoring, and policy compliance systems for:
– **outdoor media / Digital Out-Of-Home**,
– **Below-the-line marketing**,
– **retail media**,
– **media channels**,
– **on-air promotions**,
– **TV**,
– **online reputation management**,
– **social campaigns**.
Our primary objective seeks to enable corporate brand custodians, campaign leaders, and content distributors boost efficiency and profitability.
We applies cutting-edge analytics to ensure accurate analytics. By offering a integrated approach, we address key gaps of advertising efficiency, helping businesses grow in an increasingly competitive market.
Процесс получения диплома стоматолога: реально ли это сделать быстро?
LEO娛樂城無法登入？九州娛樂城退出台灣市場的真相大揭秘
近期，LEO娛樂城頻傳無法登入的消息，引發廣大玩家的疑慮與焦慮。作為九州娛樂城旗下的重要品牌，其背後的問題究竟是什麼？九州娛樂城是否真的退出台灣市場？本文將深度解析LEO娛樂城無法登入的三大原因，以及九州娛樂城退出的背景，幫助玩家了解真相並制定應對策略。
LEO娛樂城無法登入的三大原因
1. 帳號或密碼問題
部分玩家反映無法登入是由於密碼輸入錯誤或帳號遭盜用。
問題分析：這類問題通常較輕微，只需聯繫客服便可解決。
困難點：有玩家指出，LEO娛樂城的客服回應緩慢，甚至拖延處理時間，讓人懷疑是否另有隱情。
2. 平台技術或法規問題
當玩家試圖登入LEO娛樂城時，可能遇到以下情況：
伺服器無法連接或出現404錯誤頁面。
伺服器損壞或平台因法規問題遭檢舉下架，導致服務中斷。
此情況顯示平台運營出現技術或法規挑戰，玩家的遊戲體驗和資金安全因此受到影響。
3. 九州娛樂城及旗下品牌退出台灣市場
最令人震驚的原因是，LEO娛樂城可能正在退出台灣市場。
九州娛樂城因資金問題和監管壓力選擇撤出台灣。
市場傳聞指出其資金鏈出現裂痕，加上內外壓力，導致旗下品牌無法維持運營穩定性。
九州娛樂城退出台灣市場的原因
1. 市場競爭激烈，收益下滑
台灣娛樂城市場競爭日益加劇，各大品牌為爭奪市場份額不斷投入資源。九州娛樂城難以維持競爭力，收益大幅下滑，最終選擇將資源轉向其他具潛力的海外市場。
2. 資金鏈問題，運作困難
從玩家充值到出金的每個環節，九州娛樂城的資金運作均出現問題，影響平台穩定性。資金鏈斷裂使九州娛樂集團不得不低調撤出台灣，以降低損失。
3. 母公司法律與財務問題
九州娛樂集團近年來因法律與財務問題備受關注，導致其在台灣的營運面臨更多困難。相關部門的嚴格監管使得旗下品牌如LEO娛樂城、THA娛樂城被迫退出市場。
玩家如何應對LEO娛樂城無法登入的情況？
1. 立即提現本金
如果LEO娛樂城官網仍能登入，建議玩家立即提取帳戶內的所有資金，以避免因平台徹底關閉而造成損失。
2. 轉向穩定且合法的替代平台
選擇具有合法牌照和穩定運營的娛樂城作為替代平台。例如選擇國際知名品牌，確保遊戲體驗和資金安全。
3. 提高資金安全意識
在選擇新平台時，應重點關注以下事項：
資金保障措施：確保平台能提供快速出金和玩家資金保護機制。
玩家口碑：查看其他玩家的評價，選擇信譽良好的平台。
結論：面對LEO娛樂城問題，快速行動是關鍵
LEO娛樂城無法登入與九州娛樂城退出台灣市場的消息，無疑為玩家帶來了巨大不安。無論是資金問題還是伺服器故障，玩家應及時採取行動保障自身利益。立即提現資金，轉向穩定的娛樂平台，並提高安全意識，是避免損失的有效策略。
在動盪的市場環境中，選擇合法且穩定的平台是保護資金與享受遊戲體驗的最佳方式。
九州娛樂城新聞
九州集團宣布退出台灣市場 電子遊戲玩家該如何應對？
近日，九州娛樂集團正式宣布進一步調整策略，將退出台灣市場，並停止所有在台灣的運營，包括 LEO娛樂城和 THA娛樂城。這一消息無疑引起了廣泛關注，許多玩家都在懷疑接下來的遊戲體驗會受到什麼影響。
#### 退出的原因揭密
九州集團在公告中提到，退出台灣市場的原因主要包括：
1. 競爭激烈：隨著市場競爭的白熱化，越來越多的平台為了爭奪市場份額而忽略了長期的穩定經營，這導致多個平台運營問題頻出。
2. 資金流問題：部分平台在金流處理方面遭遇挑戰，無法保證玩家資金的安全與及時提款，進一步削弱了玩家的信任感。
3. 監管壓力：隨著行業規範的不斷提升，部分平台難以滿足合規要求，這直接導致服務中斷，甚至被迫退出市場。
4. 玩家需求變化：近年來，玩家對平台的穩定性、安全性和多樣化遊戲選擇的要求越來越高，只有實力雄厚的品牌才能夠滿足這些需求。
#### 轉向富遊娛樂城的好處
面對 LEO及 THA 退出的消息，九州娛樂集團也向玩家推薦了 RG 富遊娛樂城，這是一個深受玩家支持的賭場品牌。富遊娛樂城提供多項優勢，可以幫助玩家順利轉移，繼續享受遊戲體驗。
– 穩定性高：富遊娛樂城利用行業前沿的技術支持，確保平台運行穩定可靠，減少登入問題和系統故障的風險。
– 安全性強：該平台應用頂級數據加密技術，全面保護玩家的資金和個人隱私，讓玩家無後顧之憂。
– 遊戲多樣化：富遊娛樂城提供豐富的遊戲 selections，包括真人娛樂、電子遊戲、體育博彩等，能滿足不同玩家的需求。
#### 專為九州娛樂城會員設計的福利
為了保障受到 LEO及 THA 影響的玩家權益，富遊娛樂城推出了一系列回饋措施：
– VIP 等級保留：來自 LEO 和 THA 的玩家將保留或直接升級至對應的 VIP 等級，確保權益不受影響。
– 註冊優惠：新加入富遊娛樂城的玩家將獲得高達168的體驗金、100% 首存加碼及專屬新手禮包。
– 簡化轉移過程：富遊娛樂城為用戶提供簡單的轉移計劃，無需繁瑣手續，讓每位玩家可以專注於遊戲的樂趣。
### 結語
隨著九州娛樂集團宣布退出台灣市場，玩家們面臨著轉移平台的挑戰。儘管這一變化令人感到遺憾，但富遊娛樂城作為一個可靠的替代選擇，將為玩家的遊戲體驗帶來穩定的保障。玩家應該把握這一機會，迅速安排好轉移和註冊事宜，以確保不斷享受遊戲的樂趣。
Узнайте, как безопасно купить диплом о высшем образовании
Приобретение диплома ПТУ с сокращенной программой обучения в Москве
LEO娛樂城無法登入？九州娛樂城退出台灣市場的真相解析
近期，LEO娛樂城頻頻傳出無法登入的消息，並伴隨著「九州娛樂城退出市場」的傳聞，引發了廣大玩家的熱議與疑慮。作為台灣線上娛樂城市場的代表品牌之一，LEO娛樂城曾憑藉其廣泛的廣告投放和龐大的代理規模，成為許多玩家耳熟能詳的名字。然而，這一系列的問題究竟是偶發事件還是背後早有計劃？本文將帶您深入了解LEO娛樂城無法登入的原因及其對玩家的影響。
LEO娛樂城無法登入：網路熱議九州娛樂城倒閉
LEO娛樂城近期無法登入的情況似乎透露出了一個更大的訊息：該平台正在逐步退出台灣市場。隨著其營運的逐漸停擺，玩家們發現以下問題日益嚴重：
官網無法訪問：登入失敗的情況變得愈加頻繁。
註冊和儲值受限：許多玩家反映無法完成新用戶註冊，甚至現有用戶的儲值功能也開始受到限制。
經調查，這一退出決策並非偶然，而是九州娛樂城高層的長期規劃結果。讓我們一起探索這一決策背後的可能原因。
LEO娛樂城退出台灣的三大可能原因
原因一：台灣市場利潤有限，轉向海外發展
LEO娛樂城無法登入的核心原因之一，是該品牌已經決定退出台灣市場。九州娛樂城高層認為，台灣市場的競爭激烈且利潤有限，因此選擇將資源轉向其他潛力更大的海外市場以追求更高的收益。
見好就收：這一做法與許多商業決策類似，在利潤達到一定水平後選擇退出，尋求更具回報的新機會。
海外市場吸引力：國際市場的規模和成長性更具吸引力，讓九州娛樂城看到了更大的可能性。
原因二：生態鏈與資金運作出現問題
LEO娛樂城的運營生態鏈可能存在隱患，導致其無法長期穩定運作：
資金鏈斷裂：玩家的充值與出金流程可能受到影響，進一步削弱平台的穩定性。
運營成本上升：在台灣市場的高運營成本可能也是平台選擇退出的一大原因。
原因三：九州娛樂城受到法律與政策壓力
九州娛樂城近年來面臨多起法律與政策挑戰，影響了其旗下品牌的正常運營：
監管政策加強：台灣政府對線上娛樂平台的監管力度加大，對九州娛樂城造成了直接影響。
法律爭議：母公司的財務與法規問題頻頻登上新聞，使旗下品牌的經營環境更加複雜。
LEO娛樂城無法登入對玩家的影響
隨著LEO娛樂城逐步退出台灣市場，玩家需要做好以下應對措施：
迅速提現本金：如您仍可登入官網，建議立即提取帳戶內的資金，避免遭遇平台徹底關閉後的損失。
尋找可靠的替代平台：選擇擁有合法牌照且運營穩定的國際品牌，如1XBET等，確保遊戲與資金安全。
提高資金安全意識：在選擇新平台時，應重點關注其口碑、資金保障措施以及用戶評價，避免再次陷入類似情況。
結論：LEO娛樂城無法登入背後的啟示
LEO娛樂城無法登入以及九州娛樂城退出台灣市場的消息，揭示了線上娛樂市場的高風險性與不穩定性。對玩家而言，選擇安全合法的平台才是長遠之計。
在未來，隨著國際市場的開放與法規的完善，玩家或許能期待更穩定與透明的娛樂環境。但在此之前，迅速採取行動保障自己的資金與利益才是當務之急。
九州娛樂城倒了
LEO娛樂城無法登入？九州集團可能要退出台灣市場！
近期，許多玩家發現自己無法登入 LEO娛樂城，這引發了關於九州集團是否即將退出台灣市場的廣泛討論。這篇文章將深入探討可能的原因以及玩家該如何應對。
#### 為什麼 LEO娛樂城無法登入？
1. 帳號或密碼問題：這是最常見的原因之一。如果玩家忘記了密碼或帳號被鎖定，只需聯繫客服提供必要的資訊，通常能夠迅速恢復進入權限。
2. 網站故障：有不少玩家報告稱無法正常訪問 LEO娛樂城，顯示404錯誤頁面。這可能是因為網站伺服器出現問題或被檢舉。玩家在遇到此類問題時，可以詢問客服以獲取正確的網址，並建議將網址加入書籤，以便隨時訪問。
3. 九州集團計劃退出台灣市場：最令人擔憂的是，傳聞九州集團可能正在考慮退出台灣市場，這將對玩家造成直接影響，特別是在資金存款和提現上。這個情況讓不少玩家感到焦慮，也加深了對於未來的擔憂。
#### 為什麼九州集團要退出？
有幾個因素可能促使九州集團作出這樣的決定：
– 市場競爭加劇：台灣市場的競爭相當激烈，對於像 LEO這樣的品牌來說，持續獲利變得越來越困難。因此，他們或許希望尋找其他市場擴展機會。
– 金融壓力：九州集團近來因多起事件受到關注，特別是涉及金流問題。前高層的逮捕與金融查詢事件，使得旗下各平台的運作都變得更加艱難。
– 品牌形象受損：隨著負面新聞的增多，LEO和其他九州品牌的信譽也受到了相當大的影響。為了保護品牌形象，退出某個市場可能被視為一種選擇。
#### 對於玩家的建議
如果 LEO娛樂城真的面臨退出台灣市場的風險，玩家需要做好應對措施。以下是一些選擇替代平台的建議：
– 考慮其他娛樂城brand：如亞博體育，該平台具有許多優勢，包括合法的營業執照和豐富的遊戲選擇。
– 檢視平台的安全性：選擇那些擁有穩定金流和良好信譽的娛樂城，以確保資金的安全。
– 利用促銷活動：例如亞博體育提供的首次充值優惠合理，這是進一步提升棋局的好選擇。
### 結論
LEO娛樂城目前的登入問題引發了對九州集團未來的憂慮。儘管提供了恢復帳號的實用方法，玩家仍應謹慎應對，並考慮在目前市況下的其他可靠選擇，確保自己的資金安全及遊戲體驗。隨著娛樂市場的變化，選擇一家穩定、信譽良好的平台變得尤為重要。
Leo娛樂城無法登入
Leo娛樂城無法登入？是九州娛樂城倒了嗎？背後原因竟是這樣！
最近，許多玩家發現自己無法登入 Leo娛樂城，甚至有人關心是否這意味著九州娛樂城的倒閉。究竟發生了什麼事情？今天，我們將解開這個謎團，幫助大家瞭解 Leo娛樂城無法登入的真正原因。
#### 目錄
1. Leo娛樂城無法登入：背後的三個原因
2. 九州娛樂城倒了？只是退出台灣市場
3. Leo娛樂城無法登入該怎麼辦？
4. 最新娛樂城推薦排名，這幾家平台更值得信賴！
5. 結論
### Leo娛樂城無法登入：背後的三個原因
#### 原因一：帳號被鎖或密碼錯誤
最常見的問題之一就是玩家的帳號被鎖定或密碼輸錯。這類問題其實相對容易解決，玩家只需聯繫客服要求恢復帳號即可。然而，有部分玩家反映客服反應緩慢，甚至感覺客服想要拖延時間，這一點讓人不禁懷疑是否有其他貓膩。
#### 原因二：網站壞了或被檢舉
有玩家在登錄時遇到 404 錯誤，這種情況通常表明網站伺服器出現故障，或是因為某種原因被檢舉並暫時下架。這樣的情況對於玩家來說非常令人沮喪，因為缺乏官方的回應和修復時間，只能無奈等待。
#### 原因三：九州集團退出台灣市場
近期有消息指出，九州集團可能正在逐步退出台灣的市場，這可能影響到其旗下所有娛樂城的運作。如果該集團確實進行了市場撤退，則 Leo娛樂城的運作將受到直接影響，這也解釋了為什麼許多玩家會感到困惑和不安。
### 九州娛樂城倒了？只是退出台灣市場
雖然網上有許多傳言說九州娛樂城已經倒閉，但實際上應該理解為它正在退出台灣市場。這樣的變化可能與政策、法規等多種因素有關。對於玩家來說，這是需要留意的一個信息，以便尋找其他可行的娛樂選擇。
### Leo娛樂城無法登入該怎麼辦？
如果你遇到無法登入的問題，建議你首先檢查帳號和密碼是否正確。如果是技術性問題，則需等待官方的修復通知。在這段時間內，可以考慮暫時使用其他娛樂城平台，避免資金被鎖定。
### 最新娛樂城推薦排名，這幾家平台更值得信賴！
在選擇娛樂城時，建議選擇評價高、可靠性強的平台。以下是目前推薦的一些娛樂城，這幾家平台在安全性和用戶體驗上表現良好，可以作為替代選擇：
1. XXX娛樂城 – 以安全和穩定著稱。
2. YYY娛樂城 – 提供多樣化的遊戲選擇。
3. ZZZ娛樂城 – 客服反應快速，體驗佳。
### 結論
總的來說，Leo娛樂城無法登入的原因涉及帳號問題、網站技術故障以及九州集團的市場動向。希望這篇文章能幫助你更好地理解目前的情況。保持警惕，選擇可靠的娛樂平台，以確保自身的資金安全和良好的遊戲體驗。希望未來能有更好的解決方案來改善玩家的困擾！
Узнайте стоимость диплома высшего и среднего образования и процесс получения
九州娛樂城
九州娛樂城：亞洲頂級線上娛樂平台
九州娛樂城，作為亞洲領先的線上博弈平台，以其專業性、公平性和創新性著稱。在這裡，您可以享受全方位的娛樂體驗，包括體育投注、真人遊戲、電子遊戲、六合彩球以及流行的捕魚機和棋牌遊戲。九州娛樂城是台灣玩家的首選娛樂平台，被譽為業界 No.1！
九州娛樂城的亮點
1. 多元化遊戲選擇
九州娛樂城擁有超過千款來自全球頂尖供應商提供的遊戲，滿足各種類型玩家的需求。無論是喜歡競技性的體育投注、刺激的真人遊戲，還是休閒的電子遊戲，九州娛樂城都能提供最適合您的選擇。
體育投注：全面覆蓋世界級賽事，包括世界杯、職業聯賽等。提供多種投注方式，如讓球、大小、單雙、串關等，並支持桌面端與手機端投注。
真人遊戲：KU真人百家樂、LEO真人遊戲等，讓您感受現場賭桌的真實刺激。
電子遊戲與捕魚機：多款熱門遊戲，如九州熱門電子遊戲和捕魚機，帶給玩家極致娛樂享受。
六合彩與棋牌遊戲：適合策略型玩家的理想選擇。
2. 極致便利的操作體驗
九州娛樂城支持通過官方網站和九州APP下載進行操作，無論您身在何處，都可以輕鬆加入遊戲世界。針對台灣玩家的本地化設計確保操作流暢、存取款方便。
3. 先進技術與安全保障
九州娛樂城集團總部位於菲律賓首都馬尼拉的RCBC Plaza，配備世界一流的安全資訊防護系統和智能大樓自動化系統（BAS）。玩家的數據與資金安全都能得到最佳保障，讓每一次遊戲都安心無憂。
4. 熱門品牌與平台支持
九州娛樂城旗下包括三大品牌：
LEO娛樂：提供真人遊戲、體育直播及免費影城。
THA娛樂：專注於新手友好和便捷操作。
KU娛樂：以真人百家樂而著稱。
每個品牌雖分別由不同管理團隊運營，但都傳承了九州娛樂城的高標準，遊戲系統與界面毫無差異，為玩家提供無縫娛樂體驗。
為什麼選擇九州娛樂城？
專業性與公平性
九州娛樂城堅持以「即時便利、公平公正、專業營運」為宗旨，研發創新遊戲技術，滿足不同類型玩家需求。
貼近市場與玩家需求
擁有兩岸三地的精英設計師與代理團隊，根據玩家反饋持續改進產品，並為合作商提供及時更新支持。
優越的服務與保障
從遊戲操作到客戶支持，九州娛樂城提供全面的服務支持，讓每位玩家都能感受到最貼心的服務。
九州娛樂城的未來
作為線上博弈行業的領航者，九州娛樂城不斷推陳出新，致力於提供更豐富的遊戲選擇和更完善的玩家體驗。同時，透過強大的技術與營運團隊，九州娛樂城已成為台灣乃至亞洲地區娛樂平台的代名詞。
立即下載九州APP，體驗最極致的娛樂樂趣！九州娛樂城——您的最佳線上娛樂夥伴！
Купить диплом о среднем образовании в Москве и любом другом городе
Полезная информация как официально купить диплом о высшем образовании
九州娛樂城：亞洲頂級線上娛樂平台
九州娛樂城，作為亞洲領先的線上博弈平台，以其專業性、公平性和創新性著稱。在這裡，您可以享受全方位的娛樂體驗，包括體育投注、真人遊戲、電子遊戲、六合彩球以及流行的捕魚機和棋牌遊戲。九州娛樂城是台灣玩家的首選娛樂平台，被譽為業界 No.1！
九州娛樂城的亮點
1. 多元化遊戲選擇
九州娛樂城擁有超過千款來自全球頂尖供應商提供的遊戲，滿足各種類型玩家的需求。無論是喜歡競技性的體育投注、刺激的真人遊戲，還是休閒的電子遊戲，九州娛樂城都能提供最適合您的選擇。
體育投注：全面覆蓋世界級賽事，包括世界杯、職業聯賽等。提供多種投注方式，如讓球、大小、單雙、串關等，並支持桌面端與手機端投注。
真人遊戲：KU真人百家樂、LEO真人遊戲等，讓您感受現場賭桌的真實刺激。
電子遊戲與捕魚機：多款熱門遊戲，如九州熱門電子遊戲和捕魚機，帶給玩家極致娛樂享受。
六合彩與棋牌遊戲：適合策略型玩家的理想選擇。
2. 極致便利的操作體驗
九州娛樂城支持通過官方網站和九州APP下載進行操作，無論您身在何處，都可以輕鬆加入遊戲世界。針對台灣玩家的本地化設計確保操作流暢、存取款方便。
3. 先進技術與安全保障
九州娛樂城集團總部位於菲律賓首都馬尼拉的RCBC Plaza，配備世界一流的安全資訊防護系統和智能大樓自動化系統（BAS）。玩家的數據與資金安全都能得到最佳保障，讓每一次遊戲都安心無憂。
4. 熱門品牌與平台支持
九州娛樂城旗下包括三大品牌：
LEO娛樂：提供真人遊戲、體育直播及免費影城。
THA娛樂：專注於新手友好和便捷操作。
KU娛樂：以真人百家樂而著稱。
每個品牌雖分別由不同管理團隊運營，但都傳承了九州娛樂城的高標準，遊戲系統與界面毫無差異，為玩家提供無縫娛樂體驗。
為什麼選擇九州娛樂城？
專業性與公平性
九州娛樂城堅持以「即時便利、公平公正、專業營運」為宗旨，研發創新遊戲技術，滿足不同類型玩家需求。
貼近市場與玩家需求
擁有兩岸三地的精英設計師與代理團隊，根據玩家反饋持續改進產品，並為合作商提供及時更新支持。
優越的服務與保障
從遊戲操作到客戶支持，九州娛樂城提供全面的服務支持，讓每位玩家都能感受到最貼心的服務。
九州娛樂城的未來
作為線上博弈行業的領航者，九州娛樂城不斷推陳出新，致力於提供更豐富的遊戲選擇和更完善的玩家體驗。同時，透過強大的技術與營運團隊，九州娛樂城已成為台灣乃至亞洲地區娛樂平台的代名詞。
立即下載九州APP，體驗最極致的娛樂樂趣！九州娛樂城——您的最佳線上娛樂夥伴！
st666
ST666 Xổ Số – Điểm Đến Giải Trí Hoàn Hảo
ST666 Xổ Số là nền tảng giải trí trực tuyến hàng đầu, cung cấp đa dạng các loại hình trò chơi từ keno, xổ số miền Nam (XSMN), xổ số miền Bắc (XSMB) đến xổ số siêu tốc. Với dịch vụ chuyên nghiệp và an toàn, ST666 mang đến cho bạn một trải nghiệm hoàn toàn mới mẻ và hấp dẫn.
Tại Sao Nên Chọn ST666 Xổ Số
Truy Cập Nhanh Và An Toàn
ST666 đảm bảo quyền truy cập nhanh chóng thông qua đường dẫn chính thức, loại bỏ hoàn toàn rủi ro từ các trang web giả mạo hoặc nguy cơ mất tài khoản. Hệ thống bảo mật hiện đại giúp bạn yên tâm khi đăng nhập và tham gia trò chơi.
Ưu Đãi Độc Quyền Dành Cho Thành Viên
ST666 mang đến nhiều chương trình khuyến mãi đặc biệt dành riêng cho người chơi, bao gồm phần thưởng giá trị và các ưu đãi hấp dẫn. Thành viên mới sẽ được trải nghiệm các chính sách hỗ trợ vượt trội, giúp tăng cơ hội chiến thắng và tận hưởng trò chơi tốt nhất.
Bảo Mật Thông Tin Tối Đa
Hệ thống mã hóa hiện đại của ST666 đảm bảo mọi giao dịch và dữ liệu cá nhân đều được bảo vệ an toàn. Mọi thông tin đều được xử lý theo quy chuẩn bảo mật cao nhất, giúp người chơi yên tâm giải trí mà không lo lắng về vấn đề rủi ro thông tin.
Đa Dạng Trò Chơi Giải Trí
Xổ số: Từ xổ số truyền thống như XSMN, XSMB đến xổ số siêu tốc, đáp ứng mọi nhu cầu giải trí của người chơi.
Lô đề: Cung cấp giao diện dễ sử dụng, giúp bạn dễ dàng chọn số và theo dõi kết quả trực tiếp.
Casino trực tuyến: Đa dạng các trò chơi từ bài bạc, roulette đến các game đổi thưởng hiện đại.
Những Lợi Ích Khi Chơi Tại ST666
Dịch vụ hỗ trợ khách hàng chuyên nghiệp hoạt động 24/7.
Giao dịch nạp và rút tiền nhanh chóng, minh bạch.
Hệ thống cập nhật trò chơi thường xuyên, mang lại sự mới mẻ và không nhàm chán.
Nền tảng thiết kế hiện đại, thân thiện với mọi thiết bị, từ máy tính đến điện thoại di động.
Cách Truy Cập ST666
Truy cập đường dẫn chính thức của ST666 để đảm bảo an toàn.
Đăng ký tài khoản và hoàn tất các bước xác thực thông tin.
Tham gia các trò chơi hấp dẫn và tận hưởng phần thưởng đặc biệt dành cho thành viên.
ST666 Xổ Số không chỉ là nền tảng giải trí mà còn là nơi mang lại cơ hội chiến thắng và trải nghiệm dịch vụ đẳng cấp. Tham gia ngay hôm nay để khám phá một thế giới giải trí đa dạng và chuyên nghiệp!
st666
ST666 – Nhận Định Bóng Đá Kèo Nhà Cái Uy Tín
ST666: Địa Chỉ Lý Tưởng Cho Những Tín Đồ Cá Cược Bóng Đá
ST666 là nền tảng nhận định bóng đá và kèo nhà cái chuyên nghiệp, nơi người chơi có thể tham gia dự đoán các kèo đa dạng như cược tài xỉu, cược chấp, và cược 1×2. Với giao diện thân thiện, tỷ lệ cược minh bạch và ưu đãi hấp dẫn, ST666 đang dần trở thành lựa chọn hàng đầu của cộng đồng yêu bóng đá.
Nhận Định Kèo Nhà Cái Đa Dạng
Cược Tài Xỉu (#cuoctaixiu)
Dựa vào tổng số bàn thắng trong trận đấu, người chơi dễ dàng chọn lựa Tài (nhiều hơn tỷ lệ nhà cái đưa ra) hoặc Xỉu (ít hơn tỷ lệ).
ST666 cung cấp các phân tích chi tiết giúp người chơi đưa ra lựa chọn chính xác.
Cược Chấp (#cuocchap)
Thích hợp cho những trận đấu có sự chênh lệch về sức mạnh giữa hai đội. ST666 cung cấp tỷ lệ chấp tối ưu, phù hợp với cả người chơi mới và chuyên nghiệp.
Cược 1×2 (#cuoc1x2)
Phù hợp cho những ai muốn dự đoán kết quả chung cuộc (Thắng – Hòa – Thua). Đây là loại kèo phổ biến, dễ hiểu và có tỷ lệ cược hấp dẫn.
Ưu Đãi Hấp Dẫn Tại ST666
Nhận 160% tiền gửi lần đầu: Khi đăng ký tài khoản mới và nạp tiền, người chơi sẽ nhận được số tiền thưởng cực lớn, tăng cơ hội tham gia các kèo.
Hoàn tiền 3% mỗi ngày: Chính sách hoàn tiền giúp người chơi giảm thiểu rủi ro, thoải mái trải nghiệm mà không lo lắng nhiều về chi phí.
Vì Sao Nên Chọn ST666?
Nền Tảng Uy Tín: ST666 cam kết mang đến trải nghiệm cá cược minh bạch và an toàn.
Phân Tích Chuyên Sâu: Đội ngũ chuyên gia của ST666 luôn cập nhật nhận định mới nhất về các trận đấu, giúp người chơi đưa ra quyết định tối ưu.
Hỗ Trợ 24/7: Đội ngũ hỗ trợ chuyên nghiệp, luôn sẵn sàng giải đáp thắc mắc của người chơi.
Giao Dịch Nhanh Chóng: Nạp rút tiền linh hoạt, đảm bảo sự tiện lợi và bảo mật.
Cách Tham Gia ST666
Truy cập website chính thức của ST666.
Đăng ký tài khoản bằng thông tin cá nhân.
Nạp tiền lần đầu để nhận ưu đãi 160%.
Bắt đầu trải nghiệm cá cược với các kèo yêu thích!
Hãy đến với ST666 để tận hưởng không gian cá cược chuyên nghiệp, nhận định kèo chất lượng và những phần thưởng hấp dẫn. Tham gia ngay hôm nay để trở thành người chơi chiến thắng!
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт телевизоров xiaomi сервис, можете посмотреть на сайте: ремонт телевизоров xiaomi сервис
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
LEO娛樂城
LEO娛樂城：九州娛樂集團的卓越創舉與運營優勢
九州娛樂集團總部的現代化運營
九州娛樂集團的總部設於菲律賓首都馬尼拉市中心最具代表性的現代化建築「RCBC Plaza」。這座辦公大樓融合了全球領先的建築科技與安全系統，包括：
國家級資訊防護系統，確保數據安全。
樓宇自動化系統 (BAS)，實現數位化管理與高效運營，包括防火系統、光纖電訊和數位監控。
九州娛樂為員工提供舒適的工作環境和專業的教育培訓，確保服務水準一流。其員工以專業知識和親切態度，為尊貴玩家帶來極致的遊戲體驗。
LEO娛樂旗下品牌與遊戲特色
九州娛樂城旗下分支包括 LEO、THA 和 KU 三個娛樂品牌。雖然品牌各自獨立運營，但都共享相同的遊戲系統與界面，提供超過數千款來自全球頂級供應商的遊戲。
這些品牌的核心特色包括：
種類繁多的遊戲：滿足不同類型玩家的需求，包括電子遊戲、體育博彩、真人娛樂等。
不斷更新的內容：通過九州獨家技術，網站內容保持新鮮，合作商可快速更新遊戲資源，確保平台競爭力。
玩家在這些平台上可以隨時找到適合自己的遊戲，享受沉浸式的娛樂體驗。
LEO娛樂城的歷史與發展
九州娛樂集團的起源可以追溯至其最早期的經營模式：「信用版」賭博平台 《天下體育球版》。儘管該模式在當時非常流行，但因高風險與財務處理複雜而逐漸被淘汰。
隨著市場需求的變化，九州娛樂轉型為現金版平台 《天下現金網》，引入了更安全、便捷的遊戲模式。這種轉變不僅提升了玩家的體驗，也使平台得以進一步發展。
如今，九州娛樂城已成為台灣博弈業界的領軍者，不僅優化了網站版面與功能，還推出了專屬手機APP，方便玩家隨時隨地進行遊戲體驗。
LEO娛樂的成功秘訣
現代化運營與技術支持：九州娛樂在系統安全與技術更新方面投入巨大資源，確保平台運營穩定可靠。
多元化遊戲體驗：通過與全球頂級遊戲供應商合作，平台提供了豐富的遊戲選擇，適應各種玩家需求。
用戶至上：專業培訓的員工以細心和熱忱態度，提供高品質服務，讓玩家倍感尊重。
不斷創新：從信用版到現金版，再到手機APP，九州娛樂始終緊跟市場趨勢，致力於打造最佳娛樂體驗。
結語
LEO娛樂城作為九州娛樂集團旗下的重要品牌，不僅繼承了集團的核心價值，更在遊戲選擇、服務品質和技術創新方面不斷提升。從最初的《天下體育球版》到如今的行業領先者，LEO娛樂見證了九州娛樂城的發展歷程，也成為博弈行業中的耀眼明星。
加入 LEO娛樂城，感受來自九州娛樂集團的專業與熱情，享受最頂級的線上博弈體驗！
娛樂城
RG富遊娛樂城：台灣線上娛樂城的最佳選擇
RG富遊娛樂城以其卓越的服務和多樣化的遊戲選擇，成為2024年最受歡迎的線上娛樂平台。受到超過50位網紅和部落客的實測推薦，這座娛樂城不僅提供豐富的遊戲，還帶來眾多優惠活動和誠信保證，贏得了廣大玩家的信任與青睞。
RG富遊娛樂城的獨特優勢
多重優惠活動
體驗金 $168：新手玩家可以免費試玩，無需任何成本即可體驗高品質遊戲。
首儲1000送1000：首次存款即可獲得雙倍金額，增加遊戲的樂趣與機會。
線上簽到轉盤：每日簽到即可參加抽獎，贏取現金獎勵和豐厚禮品。
快速存提款與資金保障
RG富遊採用自主研發的財務系統，確保5秒快速存款，滿足玩家即時遊戲需求。
100%保證出金，杜絕任何拖延或資金安全風險，讓玩家完全放心。
遊戲種類豐富
RG富遊娛樂城涵蓋多種遊戲類型，滿足不同玩家的需求，包括：
真人百家樂：與真人荷官互動，感受真實賭場的刺激氛圍。
電子老虎機：超過數百款創新遊戲，玩法新穎，回報豐厚。
電子捕魚：趣味性強，結合策略與娛樂，深受玩家喜愛。
電子棋牌：提供公平競技環境，適合策略型玩家。
體育投注：涵蓋全球賽事，賠率即時更新，為體育愛好者提供最佳選擇。
樂透彩票：參與多地彩票，挑戰巨額獎金。
跨平台兼容性
RG富遊支持Web端、H5、iOS和Android設備，玩家可隨時隨地登錄遊戲，享受無縫體驗。
與其他娛樂城的不同之處
RG富遊以現金版模式運營，確保交易透明和安全性。相比一般娛樂城，RG富遊在存提款速度上遙遙領先，玩家可在短短15秒內完成交易，並且100%保證資金提領。而在線客服全年無休，隨時提供支持，讓玩家在任何時間都能解決問題。
相比之下，一般娛樂城多以信用版模式運營，存在出金風險，且存提款速度較慢，客服服務不穩定，無法與RG富遊的專業性相比。
為什麼選擇RG富遊娛樂城
資金交易安全無憂：採用最先進的SSL加密技術，確保每筆交易的安全性。
遊戲種類全面豐富：每日更新多樣化遊戲，帶來新鮮感和無限可能。
優惠活動力度大：從體驗金到豐厚的首儲獎勵，玩家每一步都能享受優惠。
快速存提款服務：自主研發技術保障流暢交易，遊戲不中斷。
全天候專業客服：24/7在線支持，及時解決玩家需求。
立即加入RG富遊娛樂城
RG富遊娛樂城不僅提供豐富的遊戲體驗，更以專業的服務、完善的安全保障和多樣的優惠活動，為玩家打造一個值得信賴的娛樂環境。立即註冊，體驗台灣最受歡迎的線上娛樂城！
вывод из запоя в стационаре нижний новгород вывод из запоя в стационаре нижний новгород .
вывод из запоя нижний новгород стационар вывод из запоя нижний новгород стационар .
вывод из запоя стационар вывод из запоя стационар .
вывод из запоя стационар вывод из запоя стационар .
вывода из запоя в стационаре вывода из запоя в стационаре .
娛樂城
富遊娛樂城：全台灣第一推薦的娛樂城體驗
富遊娛樂城是全台灣最受玩家推崇的娛樂平台，提供多種優惠、豐富的遊戲選擇以及高品質的服務，讓每位玩家都能享受極致的遊戲樂趣。無論您是新手還是資深玩家，富遊娛樂城都能滿足您的需求，帶給您刺激的遊戲體驗。
富遊娛樂城的優惠活動
1. 免費娛樂城體驗金
新玩家只需註冊即可免費領取 $168 元的體驗金，無需存款，便可立即體驗各種遊戲，感受遊戲帶來的樂趣。
2. 首次存款優惠
首次存款 $1000 元，即送 $1000 元遊戲金，讓您在遊戲中有更多機會獲勝，增添刺激感。
3. 新會員五選一好禮
新加入的會員可選擇五種專屬好禮之一，從遊戲金到實體獎品，讓您的遊戲旅程更加多彩。
熱門遊戲種類
富遊娛樂城提供多樣化的遊戲選擇，適合不同喜好的玩家：
電子老虎機：多款創新遊戲，讓玩家享受豐厚獎金機會。
百家樂：與真人荷官互動，體驗真實賭場的刺激感。
今彩539 和 運彩：滿足彩票愛好者的需求。
捕魚遊戲：RSG電子捕魚遊戲帶來娛樂與獎金的雙重樂趣。
熊貓體育：專為體育迷設計的多種運動投注選項。
優質服務保證
1. 出金快速、安全可靠
富遊娛樂城採用先進的財務處理系統，保證快速存提款，讓玩家不用擔心資金安全問題。
2. 技術先進的APP平台
流暢的畫面設計與設備兼容性，讓用戶輕鬆上手。
持續升級與更新，提供更多創新遊戲類型。
3. 24小時專業客服
專業客服隨時待命，為玩家解答所有遊戲相關問題，確保您在任何時間都能享受到無縫的服務體驗。
4. 安全防護到位
採用最嚴格的安全管理系統與數據加密技術，保障用戶資金與個人信息的安全。
富遊娛樂城APP：隨時隨地盡享遊戲
富遊娛樂城APP提供了便捷的遊戲途徑，支援 IOS 與 Android 設備。
簡潔易用的界面設計，讓玩家快速找到喜愛的遊戲。
即時客服支援，隨時解決您的疑問。
免費下載，無論何時何地，您都能盡享娛樂城的精彩遊戲體驗。
為什麼選擇富遊娛樂城？
優惠豐富：免費體驗金、首存優惠、新會員好禮，活動多樣。
遊戲種類齊全：從電子遊戲到真人百家樂，滿足各類玩家需求。
服務至上：專業客服、快速出金和高安全保障讓玩家安心享受遊戲。
便捷平台：富遊APP提供隨時隨地的遊戲樂趣，讓您不受限制。
立即下載 富遊娛樂城APP，體驗全台灣第一娛樂城的無限魅力！不論您是想享受遊戲樂趣還是贏取豐厚獎金，富遊娛樂城都將是您的最佳選擇！
Возможно ли купить диплом стоматолога, и как это происходит
Диплом техникума купить официально с упрощенным обучением в Москве
九州娛樂城倒了
熊貓體育：台灣娛樂市場的新星
隨著最近幾週LEO娛樂城的頻繁登入問題和九州集團宣布退出台灣市場，各大玩家開始尋求新的娛樂平台。在這樣的背景下，熊貓體育逐漸脫穎而出，成為玩家們的熱門選擇。
#### 熊貓體育的優勢
1. 穩定性與信任
熊貓體育作為一個亞洲知名的博弈品牌，擁有龐大的資本後盾，並持有多項合法的營業執照，包括歐洲馬爾他(MGA)與菲律賓(PAGCOR)的監管牌照。這些執照不僅確保了平台的合法性，也增強了玩家對平台的信任感。
2. 多元化的入金管道
熊貓體育提供了多種入金選擇，如信用卡和電子錢包等，讓玩家的資金交易更為靈活，無需擔心因為金流問題影響遊戲體驗。
3. 優惠活動吸引新玩家
該平台推出了吸引人的優惠活動，例如首儲1000元送1000元的活動，使得新玩家可以在入場時獲得額外資金，提升遊戲興趣和參與感。
4. 公平的遊戲環境
不同於某些競爭者，熊貓體育專注於提供公平的遊戲體驗，並致力於改善玩家的遊戲環境，減少風險與不確定性。
#### 未來展望
面對市場的變化，熊貓體育不僅提供安全且多元的遊戲體驗，還展示出強大的應變能力。隨著九州集團的退出，熊貓體育有機會吸引更多原本屬於LEO娛樂城的玩家，進一步擴大市場份額。
如果你正在尋找一個穩定且值得信賴的娛樂平台，不妨考慮熊貓體育，這將是你的不二選擇。隨著新賽季的開始，更多精彩的遊戲活動也將隨之而來，讓我們拭目以待！
富遊娛樂城：台灣線上賭場的創新選擇
在台灣的線上娛樂市場中，富遊娛樂城憑藉其優質的服務和多樣化的娛樂選項，迅速成為新一代玩家的首選。既有刺激的遊戲體驗，又提供了一系列具有吸引力的優惠，富遊娛樂城無疑是追求樂趣的玩家們理想的地方。
#### 優勢與特色
1. 多樣化的遊戲選擇
富遊娛樂城提供了豐富的遊戲種類，包括電子老虎機、真人百家樂、運彩投注等。不論你是老虎機的愛好者，還是熱衷於真人賭桌的玩家，這裡都能滿足你的需求。特別推薦的遊戲如DG真人百家和RSG皇家百家樂，一定能帶給你極致的遊戲體驗。
2. 吸引人的優惠活動
富遊娛樂城針對新手和老玩家都推出了多樣的優惠活動。新會員首次存款可獲得相同金額的獎金，還有額外的體驗金送出，設計友好且實惠。此外，富遊每週的簽到獎勵和天天無上限的返水活動，更是讓玩家在遊戲中能持續獲得收益。
3. 安全可靠的存取款方式
在金融交易方面，富遊娛樂城支持多種存款和提款方式，包括各大銀行轉帳、超商儲值，甚至虛擬貨幣等。最低提款金額設置靈活，保證玩家資金的安全與便捷。
4. 人性化的操作介面
富遊娛樂城的網頁與移動應用設計簡潔易用，玩家可以方便地找到所需的遊戲和優惠。無論是在電腦還是手機上，都能順利享受到遊戲的樂趣。
#### 如何開始遊戲
如果你是新手玩家，開始你的富遊體驗非常簡單。只需註冊帳號，完成首次存款，即可獲得新手優惠。無論你想嘗試電子遊戲還是真人賭局，富遊娛樂城都能讓你輕鬆上手，享受娛樂的樂趣。
#### 社會責任與防沉迷措施
富遊娛樂城深知線上賭博的風險，因此致力於推廣負責任的遊戲文化。他們提供“防沉迷”指導，以確保玩家能夠理性投注，並提供必要的幫助和資源來幫助有需求的玩家。
#### 總結
對於尋求安全、便捷和多元化娛樂城體驗的玩家，富遊娛樂城絕對是值得選擇的選項。無論你是希望徹底放鬆，還是想要體驗刺激的博弈過程，富遊娛樂城都能滿足你的期待，成為你在台灣線上娛樂市場的最佳夥伴。立即註冊並開始你的遊戲之旅吧！
滿天星娛樂城
滿天星娛樂城：全方位的線上娛樂體驗
滿天星娛樂城作為九州娛樂城旗下品牌之一，是玩家心目中備受信賴的線上娛樂平台。不僅提供豐富的遊戲選擇和吸引人的優惠，還以其合法營運的背景和快速出金的保證，成為台灣玩家的首選娛樂城之一。
滿天星娛樂城的特色與優勢
1. 合法營運，安全可靠
滿天星娛樂城持有三大國際娛樂執照，包括：
菲律賓 PAGCOR 監督競猜牌照
BVI 認證
馬爾他 MGA 認證
這些執照展現了平台的資本實力與合法性，讓玩家能夠安心享受遊戲，完全不用擔心出金問題。
2. 高品質遊戲與豐富優惠
滿天星娛樂城與九州集團旗下的LEO、THA娛樂城一樣，提供一流的遊戲品質和多樣化的優惠。
熱門遊戲推薦：電子老虎機、真人直播、運彩投注、今彩539等，滿足各類玩家需求。
優惠活動：定期推出限時回饋活動，讓玩家在遊戲中獲得更多額外收益。
3. 快速出金與高效服務
滿天星娛樂城採用先進的財務系統，確保存提款快速、安全，讓玩家能夠專注於享受遊戲，而無需擔心資金問題。專業的客服團隊24小時在線，提供即時支援。
4. 多平台兼容的APP
滿天星娛樂城提供設計貼合玩家需求的手機APP，適用於iOS與Android系統。玩家可以隨時隨地快速登入遊玩，體驗無與倫比的娛樂快感。
熱門遊戲類型一覽
滿天星娛樂城為玩家提供多樣化的遊戲選擇，滿足不同興趣和需求：
真人直播：感受真實賭場氛圍，與真人荷官互動，體驗沉浸式娛樂。
電子老虎機：多款經典與創新機台，讓玩家享受刺激的遊戲過程。
運彩投注：涵蓋世界盃、棒球、籃球等多項運動賽事，提供即時投注與直播功能。
彩票遊戲：包括今彩539、富遊彩票等，適合熱衷於彩券的玩家。
滿天星娛樂城常見問題解答
Q1. 滿天星娛樂城是否提供APP下載？
是的，滿天星娛樂城提供專屬的手機APP，支援iOS和Android系統。玩家可透過APP快速登入，隨時享受遊戲。
Q2. 滿天星娛樂城是否合法？
滿天星娛樂城擁有多項國際認證，為合法經營的線上娛樂城，並保證玩家資金的安全性與遊戲的公平性。
Q3. 無法登入滿天星娛樂城該怎麼辦？
如遇到無法登入的情況，建議玩家檢查網路狀況或聯繫24小時客服團隊獲取即時協助。
立即加入滿天星娛樂城，享受最佳娛樂體驗！
滿天星娛樂城以合法、安全、快速的服務，搭配豐富的遊戲選擇和優惠，為玩家打造出獨一無二的線上娛樂體驗。不論您是新手還是老手，都能在滿天星找到屬於自己的遊戲樂趣。現在就下載APP，隨時隨地開始您的娛樂之旅！
Introduction of Crypto Transaction Verification and Conformity Solutions
In contemporary cryptocurrency sector, maintaining deal openness and compliance with Anti-Money Laundering (AML) and KYC standards is vital. Below is an summary of well-known sites that deliver solutions for crypto deal surveillance, check, and asset security.
1. Tokenmetrics.com
Overview: Token Metrics offers cryptocurrency analysis to examine possible risk threats. This solution lets investors to review coins ahead of buying to evade potentially scam holdings. Attributes:
– Risk evaluation.
– Perfect for buyers seeking to steer clear of hazardous or fraud projects.
2. Metamask.Monitory.Center
Overview: Metamask Monitor Center allows holders to review their crypto resources for questionable transactions and standard conformity. Advantages:
– Checks coins for purity.
– Delivers warnings about potential fund locks on particular trading sites.
– Provides detailed results after address linking.
3. BestChange.ru
Overview: Bestchange.ru is a site for monitoring and verifying crypto trade deals, providing transparency and transaction security. Highlights:
– Transaction and holding observation.
– Compliance checks.
– Online interface; supports BTC and various additional digital assets.
4. AMLCheck Bot
Description: AMLCheck Bot is a portfolio tracker and anti-money laundering compliance tool that utilizes artificial intelligence algorithms to find dubious transactions. Features:
– Transfer monitoring and identity verification.
– Offered via web version and Telegram bot.
– Supports digital assets including BSC, BTC, DOGE, and more.
5. AlfaBit
Description: AlfaBit provides complete Anti-Money Laundering (AML) tools specifically made for the crypto field, supporting businesses and financial organizations in maintaining regulatory conformity. Advantages:
– Comprehensive compliance features and evaluations.
– Adheres to modern security and regulatory guidelines.
6. AMLNode
Overview: AMLNode offers AML and customer identity services for digital currency businesses, which includes transaction monitoring, sanctions validation, and evaluation. Highlights:
– Risk assessment tools and sanctions screenings.
– Valuable for ensuring safe business activities.
7. Btrace.io
Summary: Btrace AML Crypto specializes in asset check, offering transfer monitoring, sanctions checks, and help if you are a affected by fraud. Benefits:
– Useful assistance for asset restoration.
– Transaction tracking and security tools.
Dedicated USDT Check Options
Our platform also evaluates various platforms that offer validation services for crypto transfers and accounts:
– **USDT TRC20 and ERC20 Check:** Various platforms support thorough checks for USDT transfers, aiding in the detection of doubtful activity.
– **AML Validation for USDT:** Tools are provided for tracking for fraudulent transactions.
– **“Cleanliness” Validation for Wallets:** Checking of deal and account “cleanliness” is provided to detect likely threats.
**Conclusion**
Choosing the right platform for verifying and observing digital currency transactions is important for guaranteeing safety and compliance adherence. By reading our reviews, you can select the ideal service for transaction monitoring and asset protection.
Легальная покупка диплома ПТУ с сокращенной программой обучения
2024 年熱門娛樂城與活動解析
冠天下娛樂城優惠，帶來無限樂趣
在 2024 年 4 月 16 日，冠天下娛樂城推出了全新的優惠活動，旨在為玩家帶來更大的獲利機會和更高的娛樂體驗。這些優惠活動包括多種存款獎勵、會員專屬回饋以及豐富的遊戲競賽獎金，吸引了大批玩家參與。
冠天下娛樂城以其高透明度和用戶友好的政策，已成為許多玩家的首選娛樂平台。不論是新手還是老手，都能在這裡找到適合自己的遊戲和活動。
LEO娛樂城無法登入引發市場恐慌
2024 年 11 月 29 日，LEO娛樂城因技術問題出現短暫無法登入的情況，引發了廣泛關注。許多玩家擔心這是否意味著九州娛樂城的營運出現問題。
九州娛樂集團隨後發佈官方聲明，強調這僅僅是系統升級過程中的短暫問題，並承諾玩家的資金和數據安全不受任何影響。同時，九州娛樂表示將加強伺服器穩定性，確保未來類似情況不再發生。
熱門 ZG 電子遊戲——熱舞森巴老虎機
2024 年 11 月 8 日，ZG 電子遊戲推出了熱舞森巴老虎機，這款遊戲迅速成為市場上的熱門選擇。以南美熱情的森巴舞為主題，遊戲畫面充滿色彩，搭配動感的音樂，為玩家帶來視覺與聽覺的雙重享受。
遊戲亮點：
高倍數獎勵機制：每次轉盤都有機會觸發高額獎金。
特色免費遊戲：連續獲得特殊圖案即可啟動多次免費轉盤，提高獲勝機率。
適合新手與高端玩家：簡單的玩法規則與豐富的策略選擇滿足不同層級玩家的需求。
ZG 電子遊戲致力於為玩家提供創新且有趣的遊戲體驗，熱舞森巴老虎機無疑是今年最值得嘗試的遊戲之一。
2024 世界棒球 12 強賽精彩回顧
2024 年 11 月，中華隊參加了世界棒球 12 強賽，這項全球頂尖棒球賽事吸引了來自多國的球隊和球迷參與。中華隊 28 人的名單以年輕選手和經驗豐富的老將為基礎，展現了團隊的競技實力。
比賽亮點：
精彩賽程：比賽期間，中華隊展現了堅強的防守和出色的打擊表現。
門票銷售：賽事門票迅速售罄，顯示出棒球在台灣的高度受歡迎程度。
線上直播：各大平台提供了高畫質直播，讓更多球迷能夠即時觀看比賽，感受棒球魅力。
世界棒球 12 強賽不僅是比賽，更是全台灣球迷的一場盛宴，展現了棒球作為國民運動的無限魅力。
結語
從娛樂城的優惠活動到全球性的棒球賽事，2024 年對於遊戲和體育愛好者來說充滿了亮點。不論是參與冠天下娛樂城的優惠，體驗 ZG 電子遊戲的最新老虎機，還是為中華隊的棒球比賽加油，這一年都是充滿精彩與期待的一年！
выведение из запоя в нижнем новгороде выведение из запоя в нижнем новгороде .
вывод из запоя стационарно вывод из запоя стационарно .
вывод из запоя круглосуточно нижний новгород вывод из запоя круглосуточно нижний новгород .
вывод из запоя нижний новгород стационар вывод из запоя нижний новгород стационар .
наркология вывод из запоя в стационаре наркология вывод из запоя в стационаре .
THA娛樂城無法登入
九州娛樂停止營運，LEO、THA娛樂城無法登入，玩家該怎麼辦？
近期，九州娛樂城集團旗下的LEO娛樂城與THA娛樂城相繼傳出無法登入的消息，讓許多玩家陷入焦慮。隨著九州娛樂正式宣布退出台灣市場，營運結束的消息塵埃落定。這對廣大玩家而言意味著什麼？該如何處理自己的帳戶與資金？本文將為您全面解析現況並提供解決方案。
停止營運：關鍵信息一覽
關閉存款功能：從2024年12月31日中午12:00起，九州娛樂城將全面停止所有存款服務。
正常提款開放：儘管停止營運，但官方保證玩家仍可完成提款操作。
會員權益保障：九州娛樂集團承諾全力保障玩家權益，確保在停止營運前完成所有手續。
LEO、THA娛樂城無法登入的背後原因
市場規模限制
台灣市場競爭激烈，九州娛樂城認為市場成長潛力有限。相較之下，海外市場不僅人口基數大，且有更多開發機會，這成為九州轉向海外發展的關鍵動機。
金流與政策問題
近期爆發的金流醜聞為九州娛樂的運營帶來重大挑戰。例如，九州被曝利用第三方支付進行洗錢，加上相關法規收緊，讓其在台灣市場的營運空間被大幅壓縮。
品牌策略調整
九州娛樂選擇退出台灣市場，可能是為了集中資源，強化其在其他區域的競爭力。根據消息，九州旗下品牌未來將著重於更具潛力的海外市場發展。
玩家應對策略：如何保護資金與尋找替代平台？
1. 儘速完成提款
如果您的帳戶仍可登入，建議立即完成所有提款操作，確保資金安全。九州娛樂承諾提款服務不受影響，但建議提早行動避免平台完全關閉。
2. 避免假冒平台陷阱
隨著九州娛樂停止營運，市場可能會出現假冒九州品牌的詐騙網站。玩家應提高警覺，避免在非官方平台上進行任何交易。
3. 選擇可靠替代平台
為了延續遊戲體驗，玩家可考慮轉至穩定且受信賴的平台。這裡推薦RG富遊娛樂城，憑藉其安全、穩定的服務與多樣化的遊戲選擇，成為值得信賴的替代選擇。
RG富遊娛樂城：九州玩家的理想新選擇
平台優勢
快速出金：提款平均僅需3-5分鐘，效率領先業界。
高安全保障：採用與銀行相同的加密技術，確保玩家資料與資金安全。
豐富遊戲內容：從真人百家樂到彩票遊戲，應有盡有，滿足不同玩家的喜好。
專屬優惠
針對九州會員，富遊推出了無縫轉移方案：
玩家只需提供原平台的會員等級截圖，即可快速升等並享受對應的會員福利。
再見九州，展望未來
九州娛樂城退出台灣市場，雖然讓玩家感到惋惜，但這同時也為您開啟新的可能性。在選擇娛樂平台時，安全性與穩定性應始終放在首位。RG富遊娛樂城是目前玩家最值得信賴的選擇之一，不妨加入這個全新的平台，繼續享受無限的遊戲樂趣！
Купить диплом экономиста – оптимальное решение
Легальная покупка диплома ВУЗа с сокращенной программой обучения
2024 年娛樂城遊戲推薦：最夯遊戲與最佳平台選擇
隨著線上娛樂城市場的蓬勃發展，2024 年推出了多款令人興奮的遊戲和創新平台。無論是喜歡老虎機、棋牌遊戲，還是捕魚和彩票遊戲的玩家，都能在今年找到屬於自己的遊戲樂園。以下是熱門遊戲推薦與最佳娛樂城平台的詳細介紹。
2024 年最夯遊戲推薦
電子老虎機遊戲
電子老虎機一直是娛樂城的經典項目，今年更是推出了數款熱門作品：
戰神賽特：以古埃及神話為背景，擁有高倍數獎勵的特殊功能，畫面設計精美。
魔龍傳奇：玩家可探索魔龍世界，觸發驚喜獎金和免費遊戲機會。
雷神之錘：以北歐神話為主題，特色連線玩法讓每次旋轉都充滿期待。
金虎爺：寓意招財進寶，特別適合新年期間挑戰，玩法簡單但回報豐厚。
棋牌遊戲
二人麻將：適合喜歡策略性對抗的玩家，快速節奏且競爭激烈。
忍 Kunoichi：結合武士與忍者元素，讓玩家體驗獨特的棋牌競技。
捕魚遊戲
捕魚遊戲是一種結合策略和運氣的娛樂項目，玩家可以通過捕捉魚群來獲得高額獎金，同時享受視覺和操作的雙重樂趣。
彩票遊戲
彩票遊戲以簡單快捷的玩法吸引大批玩家，提供多種國內外彩種，讓玩家隨時挑戰幸運。
RG富遊娛樂城：2024 年最佳線上娛樂城推薦
在眾多娛樂城平台中，RG富遊娛樂城以其專業服務和卓越遊戲體驗，成為今年的首選平台。
平台特色
遊戲種類豐富
提供多元化遊戲選擇，包括真人視訊、電子老虎機、捕魚、棋牌和彩票遊戲，滿足所有玩家需求。
快速便捷的存提款服務
平台支持即時存款與快速提款，無需等待，確保資金安全流動。
高度安全保障
採用最先進的加密技術，保護玩家的帳戶與交易安全。
支援多平台裝置
富遊娛樂城APP 可在 iOS 和 Android 設備上使用，界面簡潔易操作，隨時隨地享受娛樂。
專業客服支援
提供 24 小時全天候客服，隨時解答玩家疑問，保障流暢的遊戲體驗。
如何開始體驗 RG 富遊娛樂城
下載富遊 APP
在官方網站免費下載 APP，支援 iOS 和 Android 設備。
註冊帳號
使用簡單步驟完成註冊，立即進入遊戲世界。
挑戰熱門遊戲
從老虎機到棋牌遊戲，選擇您喜歡的類型，挑戰高額獎金。
結語
2024 年是線上娛樂遊戲的精彩年份，從戰神賽特到二人麻將，每款遊戲都能帶給玩家不同的樂趣。而選擇像 RG富遊娛樂城 這樣的專業平台，不僅能體驗到豐富的遊戲內容，還能享受安全可靠的服務。立即下載富遊 APP，加入這個充滿驚喜的娛樂世界
Аттестат школы купить официально с упрощенным обучением в Москве
超過100間最新資訊任你看！
還在苦苦尋找安全可靠的線上娛樂城推薦名單嗎？這篇彙集了 2024 年 100 間娛樂城評價實測，為您打造最新、最真實的娛樂城排行榜！
不論您是經驗豐富的玩家還是剛入門的新手，都能在這找到最適合您的娛樂城平台。
我們從遊戲種類、優惠活動到出金速度等多個面向進行詳細評比，讓您輕鬆避開黑網，安心享受刺激的遊戲體驗！點擊查看完整排行榜，開啟您的娛樂新篇章！
排名 推薦娛樂城 推薦指數
NO.1 富遊娛樂城 ★★★★★/5.0分
NO.2 1XBET娛樂城 ★★★★★/5.0分
NO.4 九州娛樂城 ★★★★★/5.0分
NO.5 LEO娛樂城 ★★★★★/5.0分
NO.6 YABO亞博體育娛樂城 ★★★★★/5.0分
NO.7 BET365娛樂城 ★★★★★/5.0分
NO.8 PM娛樂城 ★★★★★/5.0分
NO.9 DG娛樂城 ★★★★★/5.0分
NO.10 DB娛樂城 ★★★★★/5.0分
▲此表格為五星評價推薦娛樂城
1星評價
娛樂城評價
2024 / 10 / 24
達利娛樂城｜評價介紹
達利娛樂城｜評價介紹
達利娛樂城於2023年成立，他們聲稱致力於打造一個「安全可靠」、「即時便利」、「公平公正」及「專業營運」的優質娛樂服務平台，所有個人資…
2星評價
娛樂城評價
2024 / 10 / 04
金金財寶娛樂城｜評價介紹
金金財寶娛樂城是一個由知名啦啦隊隊員林襄代言的線上賭場，採用幣商型運營方式，玩家需使用台幣儲值以獲得遊戲幣。 該平台不支持遊戲幣的直接…
2星評價
娛樂城評價
2024 / 08 / 06
帝遊娛樂城｜評價介紹精選
帝遊娛樂城｜評價介紹
帝遊娛樂城是在2022年所創立的新興品牌，網站內的排版以及網頁速度上都有著不錯的表現，對於使用者來說非常易於操作。 帝遊娛樂城的遊戲內…
3星評價
娛樂城評價
2024 / 07 / 31
客萊柏娛樂城
客萊柏娛樂城｜評價介紹
客萊柏娛樂城是一間從2020年就開始經營的線上娛樂城品牌，該品牌累積不少玩家的好口碑，遊戲種類多元且有許多常駐的優惠活動，對新手玩家非…
5星評價
娛樂城評價
2024 / 06 / 25
DB娛樂城介紹
DB娛樂城｜評價介紹
DB娛樂城，原名PM娛樂城，在2023年更名為PM。這個重新品牌的過程中，PM集團將其亞洲遊戲品牌更名為【DB多寶遊戲】，專注於提供多…
2星評價
娛樂城評價
2024 / 06 / 14
豪神娛樂城介紹
豪神娛樂城｜評價介紹
豪神娛樂城是由著名主持人吳宗憲代言的線上賭場，採取幣商型的運營模式，玩家需使用台幣充值以換取遊戲幣。 該平台沒有提供遊戲幣的直接提現方…
2星評價
娛樂城評價
2024 / 06 / 14
星城娛樂城介紹
星城娛樂城｜評價介紹
星城娛樂城是一個由知名主持人徐乃麟代言的網上賭場，採用幣商型運營方式，玩家需使用台幣儲值以獲得遊戲幣。 該平台不支持遊戲幣的直接提現，…
1星評價
娛樂城評價
2024 / 06 / 12
AT99娛樂城介紹
AT99娛樂城｜評價介紹
AT99娛樂城是TU娛樂城最新開發的娛樂城品牌，至於為何要開發一個新的品牌引起了許多網友的推測。 對此有人覺得TU娛樂城可能被抄了或者…
不推薦
娛樂城評價
2024 / 06 / 04
AF娛樂城
AF娛樂城｜評價介紹
AF娛樂城已經不存在了，不知是經營上有問題害是什麼原因，但是據我們了解此娛樂城有被詐騙的風險，請玩家多多注意！並且網路上充斥著假冒AF…
4星評價
娛樂城評價
2024 / 05 / 17
Player-KU-CASINO
KU娛樂城｜評價介紹
過去九州娛樂城以信用版起家，為台灣地區的玩家服務。但由於會員數量過於龐大，造成客服無法消化，衍伸出許多客訴與詐騙謠言。 因此，九州決定…
1星評價
娛樂城評價
2024 / 04 / 04
錢盈娛樂城
錢盈娛樂城｜評價介紹
錢盈娛樂城於2022年成立，是一個專注於現金投注的線上遊戲平台，提供了包括體育賭博、真人百家樂、老虎機、彩票和電子遊戲等多樣化的遊戲選…
不推薦
娛樂城評價
2024 / 03 / 26
F1方程式娛樂城
F1方程式娛樂城｜評價介紹
F1方程式娛樂城屬於小型線上娛樂城版，整體晚間非常簡陋而且含有諸多瑕疵以及不完善。 首先奇怪的點在於完全沒有可以註冊的地方，我們這邊猜…
不推薦
娛樂城評價
2024 / 03 / 26
CZ168娛樂城
CZ168娛樂城｜評價介紹
CZ168娛樂城在雖然在簡介中自稱有12年的經營時間。 但是經過我們實際的調查以及訪問該品牌網頁後發現，並沒有任何12年前或是更近的資…
1星評價
娛樂城評價
2024 / 03 / 25
XY娛樂城
XY娛樂城｜評價介紹
XY娛樂城是一間於2024創立的新興品牌，我們實際到訪網站發現他們的網頁只提供手機版，並未提供電腦版，可能是因應現在主流大家都是拿手機…
2星評價
娛樂城評價
2024 / 03 / 25
搖錢樹娛樂城
搖錢樹娛樂城｜評價介紹
搖錢樹娛樂城是創立於2024，是非常新的一個品牌，但是我們實際到訪網站後，他們的娛樂城完整度是不錯的。 除了有一些小缺陷，像是我們在想…
不推薦
娛樂城評價
2024 / 03 / 25
必勝娛樂城
必勝娛樂城介紹｜評價介紹
必勝娛樂城並不存在，此娛樂城有被詐騙的風險，請玩家多多注意！必勝娛樂城據我們了解過後，發現網路上也有一家叫必勝客娛樂城，是否為同夥還有…
2星評價
娛樂城評價
2024 / 03 / 25
柏客娛樂城
柏客娛樂城｜評價介紹
柏客娛樂城是一間於2023年所創立的新興線上娛樂城品牌。 據我們實際到訪該品牌網站他們的風格走的是暗色調，以視覺上及使用體驗來說給玩家…
不推薦
娛樂城評價
2024 / 03 / 25
九鑫娛樂城
九鑫娛樂城｜評價介紹
九鑫娛樂城並不存在，此娛樂城有被詐騙的風險，請玩家多多注意！ 九鑫娛樂城調查 如有玩家耳聞到或是想前往九鑫娛樂城做遊玩，Player團…
不推薦
娛樂城評價
2024 / 03 / 25
推金娛樂城
推金娛樂城｜評價介紹
推金娛樂城並不存在，此娛樂城有被詐騙的風險，請玩家多多注意！ 推金娛樂城調查 如有玩家耳聞到或是想前往推金娛樂城做遊玩，Player團…
不推薦
娛樂城評價
2024 / 03 / 25
捷冠娛樂城
捷冠娛樂城｜評價介紹
捷冠娛樂城並沒有在經營，此娛樂城有被詐騙的風險，請玩家多多注意！ 捷冠娛樂城調查 如有玩家耳聞到或是想前往捷冠娛樂城做遊玩，Playe…
不推薦
娛樂城評價
2024 / 03 / 25
歐萊雅娛樂城
歐萊雅娛樂城｜評價介紹
歐萊雅娛樂城並不存在，此娛樂城有被詐騙的風險，請玩家多多注意！ 歐萊雅娛樂城調查 如有玩家耳聞到或是想前往歐萊雅娛樂城做遊玩，Play…
不推薦
娛樂城評價
2024 / 03 / 25
MG娛樂城
MG娛樂城｜評價介紹
MG娛樂城並不存在，此娛樂城有被詐騙的風險，請玩家多多注意！據我們了解，MG娛樂城在搜尋結果上顯示的雖然是MG娛樂城但是點進去後卻是非…
不推薦
娛樂城評價
2024 / 03 / 25
JF娛樂城
JF娛樂城｜評價介紹
JF娛樂城並不存在，此娛樂城有被詐騙的風險，請玩家多多注意！目前了解到的是，JF娛樂城在網上只搜尋的到類似空包彈的網站推薦留言，而他所…
不推薦
娛樂城評價
2024 / 03 / 25
TTB娛樂城
TTB娛樂城｜評價介紹
TTB娛樂城並不存在，此娛樂城有被詐騙的風險，請玩家多多注意！ TTB娛樂城調查 如有玩家耳聞到或是想前往TTB娛樂城做遊玩，Play…
不推薦
娛樂城評價
2024 / 03 / 25
TES888娛樂城
TES888娛樂城｜評價介紹
TES8888娛樂城並不存在，此娛樂城有被詐騙的風險，請玩家多多注意！ TES888娛樂城調查 如有玩家耳聞到或是想前往TES888娛…
2星評價
娛樂城評價
2024 / 03 / 25
新世界娛樂城
新世界娛樂城｜評價介紹
新世界娛樂城是一間於2007年創立的娛樂城，至今已有將近快20年的經營時間了。 但是經營這麼久的線上娛樂城卻被網友爆出擅自洩漏會員個資…
3星評價
娛樂城評價
2024 / 03 / 22
WG娛樂城
WG娛樂城｜評價介紹
WG娛樂城是一間創立於2023年的線上娛樂城品牌，他們提供諸多遊戲選擇讓玩家能盡情在娛樂城中享受電子遊戲所帶來的愉悅。 其中較為特別的…
1星評價
娛樂城評價
2024 / 03 / 22
逸遊娛樂城
EG逸遊娛樂城｜評價介紹
EG逸遊娛樂城是一間於2023年創立的新娛樂城品牌，他們擁有眾多遊戲提供給玩家做選擇，且頻繁地釋出優惠活動，可以說是對新手玩家非常友好…
2星評價
娛樂城評價
2024 / 03 / 21
RM娛樂城
RM娛樂城｜評價介紹
RM娛樂城是由菲律賓政府的PAGCOR（菲律賓娛樂和遊戲公司）授予博彩牌照，並獲得GLI（Gaming Laboratories In…
2星評價
娛樂城評價
2024 / 03 / 21
YG娛樂城
YG娛樂城｜評價介紹
YG娛樂城應該可以說是在業界風格數一數二特殊的線上娛樂城了，整體網站採用中世紀元素下去做設計，會讓玩家誤譯為自己身處在RPG遊戲裡頭。…
2星評價
娛樂城評價
2024 / 03 / 21
SAT888西雅圖娛樂城
SAT888西雅圖娛樂城｜評價介紹
SAT888西雅圖娛樂城創立於2022年，其中他以豐富的遊戲選項聞名，但是在網頁的體驗上卻不如其他市面上那些線上娛樂城。 網頁速度較慢…
不推薦
娛樂城評價
2024 / 03 / 21
LT娛樂城
LT娛樂城｜評價介紹
LT娛樂城是一間於2022創立的線上娛樂城品牌，其中要特別注意的是，經我們網路上調查後發現此品牌常常因各種理由不給玩家出金。 網友罵聲…
不推薦
娛樂城評價
2024 / 03 / 21
8方娛樂城
8方娛樂城｜評價介紹
8方娛樂城在網頁外觀上並無太大問題，但是經我們實際訪問該品牌後，認為8方娛樂城為詐騙黑網的可能性非常大。 其中，網頁內許多按鈕設置上只…
不推薦
娛樂城評價
2024 / 03 / 20
T9娛樂城
T9娛樂城｜評價介紹
T9娛樂城相信許多人多多少少聽過，但是這邊玩家們要特別注意其實T9娛樂城是不存在的。 經我們實際訪問該品牌網站發現到，他的網站始終指向…
3星評價
娛樂城評價
2024 / 03 / 20
玖富娛樂城
玖富娛樂城｜評價介紹
玖富娛樂城是一間於2023年創立的新創品牌，他們精美的網頁以及讓人一目瞭然的排版資訊都讓人能夠清楚明瞭的找到自己想找的資訊，他們的遊戲…
不推薦
娛樂城評價
2024 / 03 / 20
致富娛樂城
致富娛樂城｜評價介紹
致富娛樂城是一間於2018年就創立的品牌，雖然經營時間也有了5年多了，但是在網路上的口碑並不是很好，甚至還傳出該娛樂城為詐騙黑網。 就…
1星評價
娛樂城評價
2024 / 03 / 20
阿拉巴娛樂城
阿拉八娛樂城｜評價介紹
阿拉八娛樂城是一間於2022年創立的線上娛樂城，相比其他線上知名娛樂城，他們的遊戲種類明顯地比其他間少很多。 這可能導致玩家在遊戲體驗…
1星評價
娛樂城評價
2024 / 03 / 20
JP娛樂城
JP娛樂城｜評價介紹
JP娛樂城是一間於2023年所創立的新興品牌，但也不知道是否也因新創品牌因而導致在網站上有許多的資訊上的不足以及BUG的出現。 這可能…
不推薦
娛樂城評價
2024 / 03 / 20
鑫巨力娛樂城
鑫巨力娛樂城｜評價介紹
有意前往鑫巨力娛樂城得玩家們需要注意！該娛樂城已於2024/03/15停止了平台服務，因此在這邊也提醒玩家不要做任何註冊以及儲值上的動…
3星評價
娛樂城評價
2024 / 03 / 20
威樂娛樂城
威樂娛樂城｜評價介紹
威樂娛樂城專門為全球華人社群設計，憑藉其全球分布的辦公室和客服中心以及合法的經營方式，深受許多遊戲愛好者的青睞。 他們提供了多樣化的遊…
3星評價
娛樂城評價
2024 / 03 / 19
GSBET娛樂城
GSBET娛樂城｜評價介紹
GSBET在系統上以及安全性的技術上有著完善的技術，他們提供了一個安全、隱私且公平的線上博彩空間。 使用國際認可的SSL 128位加密…
1星評價
娛樂城評價
2024 / 03 / 19
a8遊藝場
A8娛樂城｜評價介紹
A8娛樂城經我們調查過後以及實際訪問該品牌網頁，發現其中幾個嚴重的問題，A8娛樂城的網頁排版混亂、且該品牌相關資訊完全都沒又做任何的說…
3星評價
娛樂城評價
2024 / 03 / 19
德正娛樂城
DZ得正娛樂城｜評價介紹
DZ得正娛樂城是一間創立於2024年的新創線上娛樂城，並且他們提供了一系列豐富的遊戲選項。 從彩票、真人視訊、體育賭注到電玩遊戲等，滿…
1星評價
娛樂城評價
2024 / 03 / 19
雷亞娛樂城
雷亞娛樂城｜評價介紹
雷亞娛樂城是一間於2020年創立的線上娛樂城，但是在訪問以及遊玩過雷亞娛樂城後我們給出了一些結論，他們在娛樂城的公司營運以及該品牌公司…
1星評價
娛樂城評價
2024 / 03 / 19
FDY娛樂城
FDY娛樂城｜評價介紹
由於FDY娛樂城的官方網站未提供足夠的詳細資訊，我們高度懷疑可能是一個詐騙或不可信的平台。 官方網站上的信息過於粗略，缺乏必要的運營和…
3星評價
娛樂城評價
2024 / 03 / 19
昊陽娛樂城
昊陽娛樂城｜評價介紹
昊陽娛樂城擁有菲律賓娛樂及博彩公司（PAGCOR）頒發的執照，受其監管，致力於提供安全、公平、公正、誠信的網上投注服務。 旨在打造世界…
3星評價
娛樂城評價
2024 / 03 / 19
369娛樂城
369娛樂城｜評價介紹
369娛樂城提供一個簡潔且易於使用的應用程式，適用於iOS和Android設備，方便玩家在Google Play和App Store上…
3星評價
娛樂城評價
2024 / 03 / 18
發樂娛樂城
發樂娛樂城｜評價介紹
創立於2021年的發樂娛樂城，是一家官方運營的線上社交博弈遊戲品牌。 以「誠信、正直、玩家第一」為核心理念，致力於維護用戶權益，為玩家…
2星評價
娛樂城評價
2024 / 03 / 18
QK娛樂城
QK娛樂城｜評價介紹
QK娛樂城專為全球華人社區打造，深受眾多遊戲愛好者喜愛。他們在全球設有辦公室及客服中心，並且合法經營，確保您的遊戲體驗既安全又愉快。 …
不推薦
娛樂城評價
2024 / 03 / 18
鑽豹娛樂城
鑽豹娛樂城｜評價介紹
關於鑽豹娛樂城的詳細訊息，在該娛樂城的官網中並沒有做任何詳細的介紹，因此我們在這邊可以合理判斷此娛樂城為詐騙黑網的可能性非常高，官網中…
3星評價
娛樂城評價
2024 / 03 / 18
飛達娛樂城
飛達娛樂城｜評價介紹
飛達娛樂城，由”Wilshire Worldwide Company Limited” 營運，他們聲稱擁有菲律賓官方博彩許可，提供豐富…
2星評價
娛樂城評價
2024 / 03 / 18
FUNNY娛樂城
FUNNY娛樂城｜評價介紹
FUNNY娛樂城專為全球華人社區量身打造，贏得了眾多遊戲愛好者的喜愛。 他們遍設辦公室及客服中心於世界各地，並且保證合法經營，讓您的遊…
2星評價
娛樂城評價
2024 / 03 / 18
金博娛樂城
金博娛樂城｜評價介紹
金博娛樂城專門為全球的華人社群設計，已經贏得了許多忠實遊戲愛好者的心。 他們在世界各地都有自己的辦公室和客服中心，而且完全合法運營，讓…
不推薦
娛樂城評價
2024 / 03 / 18
V7娛樂城
V7娛樂城｜評價介紹
V7娛樂城樂是一間於2022年年末所創立的線上娛樂城品牌，據他該品牌說法，他們擁有一支堅強的自主開發團隊、客服團隊、除了能滿足玩家在娛…
3星評價
娛樂城評價
2024 / 03 / 15
SZ娛樂城
SZ娛樂城｜評價介紹
SZ娛樂城是專門為全球華人打造的，已經吸引了眾多忠實粉絲。 他們在各地設有辦公室和客服中心，都是合法經營的，所以您可以放心。 他們提供…
3星評價
娛樂城評價
2024 / 03 / 15
DOIN娛樂城
DOIN娛樂城｜評價介紹
DOIN娛樂城，這家設立在柬埔寨波貝度假村的線上遊戲天地，不僅擁有合法的博弈執照，還提供多樣化的遊戲選項，包括運動博彩、電競、真人百家…
不推薦
娛樂城評價
2024 / 03 / 11
金合發娛樂城精選
金合發娛樂城｜評價介紹
金合發娛樂城曾在線上娛樂界獲得廣泛的歡迎，享有老牌的地位。 但是，近些年來，由於玩家提出的連串投訴，其名譽不斷受損。 這些投訴主要圍繞…
5星評價
娛樂城評價
2024 / 03 / 11
RG富遊娛樂城精選
富遊娛樂城｜評價介紹
隨著2024年的到來，最新的線上娛樂平台排行榜已經更新，這一次的排名綜合考慮了各種因素，包括體驗金、促銷活動、提款效率和遊戲多樣性，目…
不推薦
娛樂城評價
2024 / 03 / 08
3A娛樂城精選
3A娛樂城｜評價介紹
3A娛樂城是一家線上遊戲平台，提供多樣化的遊戲選擇，包括百家樂、老虎機和運彩等。 但因為網路上對這個平台的評論不多，有些人可能會擔心遭…
1星評價
娛樂城評價
2024 / 03 / 08
FA8娛樂城
FA8娛樂城｜評價介紹
FA8娛樂城在亞洲地區受到許多玩家的青睞，FA8娛樂城是一個多元化的線上賭博平台。 它提供了包羅萬象的遊戲選項，從體育投注、電玩遊戲到…
2星評價
娛樂城評價
2024 / 03 / 08
BU娛樂城
BU娛樂城｜評價介紹
BU娛樂城在亞太地區的線上娛樂市場擁有豐富的經驗，以強大的研發團隊和優質的客服服務而聞名。 該平台所開發的遊戲經美國TST技術測試機構…
5星評價
娛樂城評價
2024 / 03 / 08
1XBET娛樂城1
1XBET娛樂城｜評價介紹
1XBET娛樂城擁有許多各式各樣的遊戲和促銷活動，讓玩家每天都有機會贏得獎勵。 這個平台支持多種付款方式，包括Visa、Masterc…
不推薦
娛樂城評價
2024 / 03 / 07
大老爺娛樂城精選
大老爺娛樂城｜評價介紹
大老爺娛樂城之前的活動是你存1000元就送你1000點，但得玩到13倍投注額。 最近他們改成了存3000送1688點，但要玩到11倍投…
3星評價
娛樂城評價
2024 / 03 / 07
AC1娛樂城精選
AC1娛樂城介紹｜評價介紹
AC1娛樂城在亞太區的線上娛樂市場上運營多年，擁有一支自研團隊和專業的客服團隊。這家娛樂城努力為玩家提供一個全面、可信賴的網絡遊戲體驗…
3星評價
娛樂城評價
2024 / 03 / 07
大福娛樂城精選
大福娛樂城｜評價介紹
大福娛樂城是個網上賭博平台，玩家在這裡是用虛擬的點數來充值，算是一種幣商型的賭場。 這裡沒有直接的提款方式，玩家得自己找幣商換成現金，…
5星評價
娛樂城評價
2024 / 03 / 07
九州娛樂城
九州娛樂城｜評價介紹
九州娛樂城，也被稱作LEO娛樂城，致力於打造一個既安全又方便、公平公正的高品質娛樂服務平台。 他們的目標是創造全新的線上娛樂城體驗，普…
5星評價
娛樂城評價
2024 / 03 / 07
LEO娛樂城精選
LEO娛樂城｜評價介紹
LEO娛樂城，也被稱為”九州娛樂城“，而他們的品牌宗旨是建立一個既安全又方便的高品質線上娛樂平台。 全力為玩家提供一個公平、正義的遊戲…
1星評價
娛樂城評價
2024 / 03 / 06
金鈦城娛樂城精選
金鈦城娛樂城｜評價介紹
金鈦城娛樂城是台灣線上娛樂城(現金版)，成立於 2023年，主打高額賠率、多樣遊戲、快速出金等特色。 但多數玩家反映金鈦城娛樂城的客服…
3星評價
娛樂城評價
2024 / 03 / 06
必贏娛樂城精選
必贏娛樂城｜評價介紹
必贏娛樂城，定位為針對全球華人市場的高級線上娛樂平台，具有豐富的跨國經營經驗。 這個平台在世界各地都設有辦公室和客服中心，並且擁有多個…
3星評價
娛樂城評價
2024 / 03 / 06
好玩娛樂城
好玩娛樂城｜評價介紹
對於正在尋找高品質線上賭場的玩家來說，好玩娛樂城絕對值得一試！這個平台已經吸引了成千上萬的玩家，以提供令人興奮的賭博體驗而著稱。 好玩…
不推薦
娛樂城評價
2024 / 03 / 06
BOK娛樂城精選
BOK娛樂城｜評價介紹
目前在BOK娛樂城的網站上找不到登入的選項，當點擊相應連結時，會被重定向到【FM富馬】網站。這情況引起了疑慮，使人懷疑BOK娛樂城可能…
3星評價
娛樂城評價
2024 / 03 / 06
JY娛樂城精選
JC娛樂城｜評價介紹
JC娛樂城是九州娛樂集團下的一個品牌。但當用戶試圖註冊JC娛樂城時，他們實際上會被導向到THA娛樂城的介面，這個介面和九州娛樂城的長得…
ST666
ST666 – Sân Chơi Nổ Hũ Uy Tín Đổi Thưởng Hàng Đầu
ST666 là một trong những sân chơi nổ hũ đổi thưởng được yêu thích nhất hiện nay. Với các sảnh quay nổi tiếng như JILI Slot, PG Slot, và JDB Slot, nền tảng này không chỉ mang đến trải nghiệm giải trí đỉnh cao mà còn mang lại cơ hội đổi thưởng hấp dẫn cho người chơi.
Lý do nên chọn ST666
1. Khuyến mãi hấp dẫn
ST666 thường xuyên triển khai các chương trình ưu đãi đặc biệt:
Hoàn tiền 1.5% mỗi ngày khi quay slot, gia tăng cơ hội thắng lớn.
Chiết khấu nạp tiền lên đến 25.000.000 VNĐ, hỗ trợ tối đa cho người chơi muốn tăng vốn.
2. Sảnh quay đa dạng
ST666 mang đến hàng loạt tựa game slot từ các sảnh quay danh tiếng:
JILI Slot: Tỷ lệ thắng cao, giao diện đẹp mắt.
PG Slot: Đồ họa ấn tượng, chủ đề phong phú.
JDB Slot: Dành cho những ai yêu thích cảm giác hồi hộp.
3. Nền tảng uy tín, bảo mật cao
ST666 luôn đảm bảo an toàn cho người chơi:
Bảo mật thông tin tuyệt đối nhờ vào công nghệ mã hóa hiện đại.
Nạp/rút tiền nhanh chóng, hỗ trợ giao dịch linh hoạt mà không gián đoạn trải nghiệm.
4. Dịch vụ khách hàng chuyên nghiệp
Đội ngũ hỗ trợ của ST666 làm việc 24/7, luôn sẵn sàng giải đáp mọi thắc mắc và hỗ trợ người chơi trong suốt quá trình tham gia.
Hướng dẫn tham gia ST666
Đăng ký tài khoản: Hoàn tất các bước đăng ký dễ dàng để tham gia nền tảng.
Nhận khuyến mãi: Người chơi mới có thể nhận thưởng nạp đầu 100%.
Lựa chọn trò chơi yêu thích: Từ slot, nổ hũ đến các trò đổi thưởng khác, ST666 đều có sẵn để đáp ứng mọi nhu cầu.
Thông tin về ST666
Địa chỉ: 317 Bình Thành, Bình Hưng Hoà B, Bình Tân, Thành phố Hồ Chí Minh.
ST666 – Điểm Đến Giải Trí Và Đổi Thưởng Hàng Đầu
ST666 không chỉ là một sân chơi slot mà còn là hệ sinh thái giải trí toàn diện với dịch vụ chuyên nghiệp và ưu đãi vượt trội. Tham gia ngay hôm nay để trải nghiệm sự uy tín và cơ hội thắng lớn mà nền tảng này mang lại!
Легальная покупка школьного аттестата с упрощенной программой обучения
3A娛樂城
3A娛樂城：全方位線上娛樂體驗的首選平台
3A娛樂城作為台灣最受歡迎的線上娛樂平台之一，以其多樣化的遊戲選擇、創新的技術、以及卓越的安全保障，贏得了玩家的高度信任與青睞。無論您是新手還是老手，3A娛樂城都能滿足您的需求，帶給您獨一無二的遊戲體驗。
熱門娛樂城遊戲一覽
3A娛樂城提供多種熱門遊戲，適合不同類型的玩家：
真人百家樂：體驗真實賭場的氛圍，與真人荷官互動，感受賭桌上的緊張與刺激。
彩票投注：涵蓋多種彩票選項，滿足彩券愛好者的需求，讓您隨時隨地挑戰幸運。
棋牌遊戲：從傳統的麻將到現代化的紙牌遊戲，讓玩家在策略與運氣中找到平衡。
3A娛樂城的核心價值
1. 專業
3A娛樂城每日提供近千場體育賽事，並搭配真人百家樂、彩票彩球、電子遊戲等多種類型的線上賭場遊戲。無論您的遊戲偏好為何，這裡總有一款適合您！
2. 安全
平台採用128位加密技術和嚴格的安全管理體系，確保玩家的金流與個人資料完全受保護，讓您可以放心遊玩，無需擔憂安全問題。
3. 便捷
3A娛樂城是全台第一家使用自家開發的全套終端應用的娛樂城平台。無論是手機還是電腦，玩家都能享受無縫的遊戲體驗。同時，24小時線上客服隨時為您解決任何問題，提供貼心服務。
4. 安心
由專業工程師開發的財務處理系統，為玩家帶來快速的存款、取款和轉帳服務。透過獨立網路技術，平台提供優化的網路速度，確保每一次操作都流暢無比。
下載3A娛樂城手機APP
為了提供更便捷的遊戲體驗，3A娛樂城獨家開發了功能齊全的手機APP，讓玩家隨時隨地開啟遊戲。
現代化設計：新穎乾淨的介面設計，提升使用者體驗。
跨平台支持：完美適配手機與電腦，讓您輕鬆切換設備，無需中斷遊戲。
快速下載：掃描專屬QR碼即可進入下載頁面，立即開始暢玩！
3A娛樂城的其他服務
娛樂城教學：詳細的操作指導，讓新手也能快速上手。
責任博彩：提倡健康娛樂，確保玩家在遊戲中享受樂趣的同時，不失理性。
隱私權政策：嚴格遵守隱私保護條例，保障玩家的個人信息安全。
立即加入3A娛樂城，享受頂級娛樂體驗！
如果您正在尋找一個專業、安全、便捷又安心的線上娛樂平台，那麼3A娛樂城絕對是您的不二之選。現在就下載手機APP，隨時隨地開啟您的娛樂旅程，享受無限的遊戲樂趣與刺激！
Официальное получение диплома техникума с упрощенным обучением в Москве
вывод из запоя в стационаре нижний новгород вывод из запоя в стационаре нижний новгород .
вывод из запоя круглосуточно нижний новгород вывод из запоя круглосуточно нижний новгород .
вывод из запоя в стационаре нижний новгород вывод из запоя в стационаре нижний новгород .
кухня купить кухня купить .
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
valif online trouble – sustiva 20mg uk buy sinemet 10mg for sale
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
Как не стать жертвой мошенников при покупке диплома о среднем полном образовании
Диплом пту купить официально с упрощенным обучением в Москве
Узнайте стоимость диплома высшего и среднего образования и процесс получения
Купить диплом Барнаул
Полезные советы по покупке диплома о высшем образовании без риска
капельница от запоя капельница от запоя .
вывод запой нижний вывод запой нижний .
капельница от запоя цена капельница от запоя цена .
капельница от похмелья цена капельница от похмелья цена .
капельница от запоя на дому капельница от запоя на дому .
娛樂城
富遊娛樂城評價:2024年最新評價
推薦指數 : ★★★★★ ( 5.0/5 )
富遊娛樂城作為目前最受歡迎的博弈網站之一，在台灣擁有最高的註冊人數。RG富遊以安全、公正、真實和順暢的品牌保證，贏得了廣大玩家的信賴。
富遊線上賭場不僅提供了豐富多樣的遊戲種類，還有眾多吸引人的優惠活動。在出金速度方面，獲得無數網紅和網友的高度評價，確保玩家能享有無憂的博弈體驗。
推薦要點
新手首選: 富遊娛樂城，2024年評選首選，提供專為新手打造的豐富教學和獨家優惠。
一存雙收: 首存1000元，立獲1000元獎金，僅需1倍流水，新手友好。
免費體驗: 新玩家享免費體驗金，暢遊各式遊戲，開啟無限可能。
優惠多元: 活動豐富，流水要求低，適合各類型玩家。
玩家首選: 遊戲多樣，服務優質，是新手與老手的最佳賭場選擇。
免費試玩
富遊娛樂城詳情資訊
賭場名稱 : RG富遊
創立時間 : 2019年
賭場類型 : 現金版娛樂城
博弈執照 : 馬爾他牌照(MGA)認證、英屬維爾京群島(BVI)認證、菲律賓(PAGCOR)監督競猜牌照
遊戲類型 : 真人百家樂、運彩投注、電子老虎機、彩票遊戲、棋牌遊戲、捕魚機遊戲
存取速度 : 存款5秒 / 提款3-5分
軟體下載 : 支援APP，IOS、安卓(Android)
線上客服 : 需透過官方LINE
富遊娛樂城優缺點
優點 缺點
台灣註冊人數NO.1線上賭場
首儲1000贈1000只需一倍流水
擁有體驗金免費體驗賭場
網紅部落客推薦保證出金線上娛樂城
需透過客服申請體驗金
富遊娛樂城存取款方式
存款方式 取款方式
提供四大超商(全家、7-11、萊爾富、ok超商)
虛擬貨幣ustd存款
銀行轉帳(各大銀行皆可)
網站內申請提款及可匯款至綁定帳戶
現金1:1出金
富遊娛樂城平台系統
真人百家 — RG真人、DG真人、歐博真人、DB真人(原亞博/PM)、SA真人、OG真人、WM真人
體育投注 — SUPER體育、鑫寶體育、熊貓體育(原亞博/PM)
彩票遊戲 — 富遊彩票、WIN 539
電子遊戲 —RG電子、ZG電子、BNG電子、BWIN電子、RSG電子、GR電子(好路)、ATG電子
棋牌遊戲 —ZG棋牌、亞博棋牌、好路棋牌、博亞棋牌、RG棋牌
捕魚遊戲 —ZG捕魚、RSG捕魚、好路GR捕魚、DB捕魚
富遊娛樂城優惠活動
優惠 獎金贈點 流水要求
免費體驗金 $168 1倍 (儲值後) /36倍 (未儲值)
首儲贈點 $1000 1倍流水
返水活動 0.3% – 0.7% 無流水限制
簽到禮金 $666 20倍流水
好友介紹金 $688 1倍流水
回歸禮金 $500 1倍流水
免費試玩
專屬富遊VIP特權
黃金 黃金 鉑金 金鑽 大神
升級流水 300w 600w 1800w 3600w
保級流水 50w 100w 300w 600w
升級紅利 $688 $1080 $3888 $8888
每週紅包 $188 $288 $988 $2388
生日禮金 $688 $1080 $3888 $8888
反水 0.4% 0.5% 0.6% 0.7%
娛樂城常見問題解答（FAQ）
Q1：如何在富遊娛樂城進行首次存款？
A1：可以透過超商、虛擬貨幣或銀行轉帳進行存款，過程簡單快速。（ 詳細可查看：富遊娛樂城存款教學）
Q2：富遊娛樂城提款需要多久時間？
A2：提款過程一般在3-5分鐘內完成，保證快速到賬。（ 詳細可查看：富遊娛樂城提款教學）
娛樂城
LEO娛樂城無法登入? 九州娛樂倒了? 富遊推出無痛轉移VIP優惠
LEO娛樂城無法登入免驚！推薦RG富遊更穩定、玩的更安心！
只要是玩過線上娛樂城的玩家，一定都對Leo娛樂城不陌生，近期Leo娛樂城無法登入的狀況越來越頻繁，是因為九州娛樂城與旗下品牌將在 2024/12/31 結束營業！
由於九州娛樂城旗下擁有leo娛樂城、THA娛樂城等品牌，這波風暴也讓許多玩家人心惶惶，擔心自己的遊戲權益受損，在文章的最後我們也提供了解決方案，趕快往下看！
九州娛樂城倒閉 ? 退出台灣娛樂市場？為何 ?
最近許多玩家發現 leo娛樂城無法登入，甚至傳出九州娛樂城要退出台灣的消息！雖然官方尚未發布正式聲明，但多方消息指出，九州娛樂城 (包含THA娛樂城、leo娛樂城) 正在逐步退出台灣市場。這可能是多重因素共同作用的結果：
退出台灣市場，尋求其他發展空間
九州娛樂認為台灣市場太小，品牌之間又過於競爭，市場規模有限，九州旗下其KU體育甚至贊助過足球五大聯賽，展現雄厚實力，促使九州娛樂城將目光投向海外。
畢竟，海外市場人口基數更大，獲利潛力也更為可觀。LEO娛樂城在台灣一個月就能獲利一億，進軍海外後的收益想必更加驚人。
金流問題、警界醜聞成導火線
LEO娛樂城高度仰賴金流公司運作，近期爆發的陳政谷案件揭露其旗下公司利用第三方支付協助母公司九州洗錢。
案情更指向警界內鬼，前台中刑大隊長林明佐涉嫌收賄超過4451萬元，為九州通風報信。 九州娛樂城曾出現凌晨時段無法儲值的狀況，很可能與警方查緝行動有關。
九州娛樂的新聞事件頻傳
LEO是九州集團底下的，陳政谷被抓之後，事情鬧得很大，為了避風頭，乾脆退出台灣也很合理。
這個說法也被推算也被網友認為有高度可能，不過也有人傳說其他幹部有接手的可能，至少沒辦法完全的說死九州會採取什麼行動。
leo娛樂城無法登入的問題，或許只是冰山一角，背後可能隱藏著更深層的原因。無論如何，九州娛樂城退出台灣市場，對玩家來說都是一個警訊。
九州娛樂城宣布12/31結束營業！玩家請停止儲值、立刻提款
九州娛樂城官方宣佈，近期旗下 THA、Leo 娛樂城無法登入，是因為九州集團將正式在 2024/12/31 中午 12:00 結束營業，退出台灣市場。
在這邊提醒玩家們立即停止存款動作，並且馬上將帳戶內的資金提領出來，避免您的權益受到損害！
LEO娛樂城無法登入? 九州娛樂倒了? 富遊推出無痛轉移VIP優惠
九州娛樂城宣布在12/31結束營業
告別Leo娛樂城無法登入煩惱！玩家無痛轉移至富遊，享更多優惠！
面對leo娛樂城無法登入的窘境，以及九州娛樂城的不確定性，玩家們需要一個安全可靠的新選擇！富遊娛樂城是您最佳的選擇，我們提供：
穩定安全保證出金： 穩定安全，保證出金！ 擁有合法牌照和完善的監管機制，保障您的資金安全。
豐富多元的遊戲： 提供各式各樣的熱門遊戲，包括真人 casino、體育博彩、電子遊戲、彩票等等，滿足玩家的不同需求。
優渥的優惠活動： 新會員享有豐厚首存紅利，還有不定期的優惠活動和返水獎勵，讓您玩得更盡興！
24小時專業客服： 隨時為您解答問題，提供貼心服務。
立即註冊
特別優惠： 針對THA和LEO會員，富遊娛樂城推出獨家福利！
只要您是THA或LEO的會員，即可在富遊娛樂城直接升等到相對應的等級，並享有更高的反水、每週紅包和生日禮金！
立即加入富遊娛樂城，享受更優渥的回饋和更安心的保障！
以下是不同階級 VIP 的轉換福利與說明：
福利項目 / VIP階級 大神 金鑽 鉑金 黃金
每週紅包 2388 988 288 188
生日禮金 8888 3888 1080 688
返水 0.7 0.6 0.5 0.4
無論個人或團體，如有任何濫用本公司優惠的行為，本公司有權取消及收回獎金。
所有活動優惠都是特別為玩家而設立，在玩家註冊資訊有爭議時，為確保雙方利益，杜絕身份盜用行為，本公司有權要求玩家提供充足資訊，並以各種方式辨別玩家是否符合資格享有活動優惠。
本公司在會員有重複申請帳號行為時，有權取消及收回獎金。每位玩家、每一住址、每一電子郵箱、每一電話號碼、相同支付卡/信用卡號碼及共享電腦環境(例如網咖、其他公用網絡、公用電腦)只能擁有一個活動優惠資格。
每週限時紅包：會員在上週有過至少1次的存款記錄，每週一中午自動發放(1倍流水即可託售)，限時48小時內領取! 每週至少存款要求：黃金富遊 1,000 點，鉑金富遊 1,500點，金鑽富遊 2,500點，大神富遊 5,000點 (存款計算週期：每週一 12:00 至下週一 11:59)
生日禮金：會員在註冊三個月內過生日，今年將不能領取生日禮金。另註冊時間大於三個月的會員需在生日當月找遊戲客服領取，每年可領取一次，需提供身分證明文件核實(1倍流水即可託售)
活動如有任何異動，本公司有權在任何時間修改、暫停或取消優惠活動，無需特別通知並保留本活動最終解釋權。
轉換平台申請辦法：提供螢幕錄影原平台層級介面到戶名、手機等資訊，傳送給富遊客服進行審核。
富遊娛樂城，值得您信賴的線上娛樂平台！
我們深知玩家選擇娛樂城的首要考量是安全和信譽。富遊娛樂城以誠信為本，致力於為玩家打造一個公平、公正、透明的遊戲環境。告別leo娛樂城無法登入的煩惱，立即加入富有娛樂城，體驗最優質的線上娛樂體驗！
RG富遊娛樂城：台灣線上娛樂城的最佳選擇
RG富遊娛樂城以其卓越的服務和多樣化的遊戲選擇，成為2024年最受歡迎的線上娛樂平台。受到超過50位網紅和部落客的實測推薦，這座娛樂城不僅提供豐富的遊戲，還帶來眾多優惠活動和誠信保證，贏得了廣大玩家的信任與青睞。
RG富遊娛樂城的獨特優勢
多重優惠活動
體驗金 $168：新手玩家可以免費試玩，無需任何成本即可體驗高品質遊戲。
首儲1000送1000：首次存款即可獲得雙倍金額，增加遊戲的樂趣與機會。
線上簽到轉盤：每日簽到即可參加抽獎，贏取現金獎勵和豐厚禮品。
快速存提款與資金保障
RG富遊採用自主研發的財務系統，確保5秒快速存款，滿足玩家即時遊戲需求。
100%保證出金，杜絕任何拖延或資金安全風險，讓玩家完全放心。
遊戲種類豐富
RG富遊娛樂城涵蓋多種遊戲類型，滿足不同玩家的需求，包括：
真人百家樂：與真人荷官互動，感受真實賭場的刺激氛圍。
電子老虎機：超過數百款創新遊戲，玩法新穎，回報豐厚。
電子捕魚：趣味性強，結合策略與娛樂，深受玩家喜愛。
電子棋牌：提供公平競技環境，適合策略型玩家。
體育投注：涵蓋全球賽事，賠率即時更新，為體育愛好者提供最佳選擇。
樂透彩票：參與多地彩票，挑戰巨額獎金。
跨平台兼容性
RG富遊支持Web端、H5、iOS和Android設備，玩家可隨時隨地登錄遊戲，享受無縫體驗。
與其他娛樂城的不同之處
RG富遊以現金版模式運營，確保交易透明和安全性。相比一般娛樂城，RG富遊在存提款速度上遙遙領先，玩家可在短短15秒內完成交易，並且100%保證資金提領。而在線客服全年無休，隨時提供支持，讓玩家在任何時間都能解決問題。
相比之下，一般娛樂城多以信用版模式運營，存在出金風險，且存提款速度較慢，客服服務不穩定，無法與RG富遊的專業性相比。
為什麼選擇RG富遊娛樂城
資金交易安全無憂：採用最先進的SSL加密技術，確保每筆交易的安全性。
遊戲種類全面豐富：每日更新多樣化遊戲，帶來新鮮感和無限可能。
優惠活動力度大：從體驗金到豐厚的首儲獎勵，玩家每一步都能享受優惠。
快速存提款服務：自主研發技術保障流暢交易，遊戲不中斷。
全天候專業客服：24/7在線支持，及時解決玩家需求。
立即加入RG富遊娛樂城
RG富遊娛樂城不僅提供豐富的遊戲體驗，更以專業的服務、完善的安全保障和多樣的優惠活動，為玩家打造一個值得信賴的娛樂環境。立即註冊，體驗台灣最受歡迎的線上娛樂城！
富遊娛樂城：全台灣第一推薦的娛樂城體驗
富遊娛樂城是全台灣最受玩家推崇的娛樂平台，提供多種優惠、豐富的遊戲選擇以及高品質的服務，讓每位玩家都能享受極致的遊戲樂趣。無論您是新手還是資深玩家，富遊娛樂城都能滿足您的需求，帶給您刺激的遊戲體驗。
富遊娛樂城的優惠活動
1. 免費娛樂城體驗金
新玩家只需註冊即可免費領取 $168 元的體驗金，無需存款，便可立即體驗各種遊戲，感受遊戲帶來的樂趣。
2. 首次存款優惠
首次存款 $1000 元，即送 $1000 元遊戲金，讓您在遊戲中有更多機會獲勝，增添刺激感。
3. 新會員五選一好禮
新加入的會員可選擇五種專屬好禮之一，從遊戲金到實體獎品，讓您的遊戲旅程更加多彩。
熱門遊戲種類
富遊娛樂城提供多樣化的遊戲選擇，適合不同喜好的玩家：
電子老虎機：多款創新遊戲，讓玩家享受豐厚獎金機會。
百家樂：與真人荷官互動，體驗真實賭場的刺激感。
今彩539 和 運彩：滿足彩票愛好者的需求。
捕魚遊戲：RSG電子捕魚遊戲帶來娛樂與獎金的雙重樂趣。
熊貓體育：專為體育迷設計的多種運動投注選項。
優質服務保證
1. 出金快速、安全可靠
富遊娛樂城採用先進的財務處理系統，保證快速存提款，讓玩家不用擔心資金安全問題。
2. 技術先進的APP平台
流暢的畫面設計與設備兼容性，讓用戶輕鬆上手。
持續升級與更新，提供更多創新遊戲類型。
3. 24小時專業客服
專業客服隨時待命，為玩家解答所有遊戲相關問題，確保您在任何時間都能享受到無縫的服務體驗。
4. 安全防護到位
採用最嚴格的安全管理系統與數據加密技術，保障用戶資金與個人信息的安全。
富遊娛樂城APP：隨時隨地盡享遊戲
富遊娛樂城APP提供了便捷的遊戲途徑，支援 IOS 與 Android 設備。
簡潔易用的界面設計，讓玩家快速找到喜愛的遊戲。
即時客服支援，隨時解決您的疑問。
免費下載，無論何時何地，您都能盡享娛樂城的精彩遊戲體驗。
為什麼選擇富遊娛樂城？
優惠豐富：免費體驗金、首存優惠、新會員好禮，活動多樣。
遊戲種類齊全：從電子遊戲到真人百家樂，滿足各類玩家需求。
服務至上：專業客服、快速出金和高安全保障讓玩家安心享受遊戲。
便捷平台：富遊APP提供隨時隨地的遊戲樂趣，讓您不受限制。
立即下載 富遊娛樂城APP，體驗全台灣第一娛樂城的無限魅力！不論您是想享受遊戲樂趣還是贏取豐厚獎金，富遊娛樂城都將是您的最佳選擇！
Leo娛樂城無法登入？全面解析與解決指南
近期，Leo娛樂城的玩家紛紛反映登入失敗的情況，引發了廣泛的討論與擔憂。作為九州娛樂城旗下知名品牌之一，Leo娛樂城在台灣的娛樂市場中擁有大量用戶。然而，隨著九州娛樂城宣布將於2024年12月31日退出台灣市場，這一消息無疑讓玩家對資金安全與遊戲體驗產生了極大疑慮。
本文將深入探討Leo娛樂城無法登入的原因，提供解決方案，並推薦可靠的替代娛樂平台。
Leo娛樂城無法登入的三大原因
1. 帳號密碼問題
可能情況：最常見的原因是玩家輸入了錯誤的帳號或密碼，或者帳號被盜用。
解決方法：確認輸入的帳密正確，若仍無法登入，聯繫客服即可解決。
2. 網頁技術問題
可能情況：官網可能因伺服器維護或技術故障出現404錯誤，導致玩家無法登入。
解決方法：耐心等待官網修復，並清除瀏覽器快取和Cookie，或嘗試使用其他瀏覽器。
3. 九州娛樂城退出台灣市場
可能情況：隨著九州娛樂城宣布退出台灣市場，Leo娛樂城的營運也逐步停止，導致玩家無法再使用該平台。
影響：玩家可能面臨資金提取困難，需及時完成出金操作以保障自身利益。
娛樂城無法登入的緊急解決方案
核對帳號與密碼：確認輸入正確無誤，避免由於簡單疏忽造成的登入失敗。
檢查網路連線：確保網路穩定，必要時切換至更穩定的網路環境。
清除瀏覽器快取與Cookie：解決瀏覽器相關問題，恢復正常登入。
嘗試其他瀏覽器或設備：更換設備或使用不同瀏覽器，查看是否可以正常登入。
九州娛樂城退出台灣市場的原因
市場利潤有限：九州娛樂城認為台灣市場的競爭激烈且利潤有限，因此選擇退出並專注於其他海外市場。
資金生態鏈斷裂：現金交易平台出現問題，導致九州娛樂城難以維持正常運營。
母公司法律爭議：九州娛樂城母公司近年來因財務與法律問題受到高度關注，進一步影響旗下品牌的營運。
Leo娛樂城會員如何安全出金？
在九州娛樂城停止營運前，玩家需要立即完成出金操作以確保資金安全。
出金建議：
儘快登入官網提交提款申請，確保資金安全轉出。
若官網無法訪問，請嘗試聯繫客服，並保留交易證明以備進一步處理。
推薦替代平台：富遊娛樂城
隨著Leo娛樂城的退出，玩家可以考慮轉至穩定且值得信賴的替代平台，如富遊娛樂城。
富遊娛樂城的優勢
穩定可靠：擁有先進的技術和完善的資金保障機制，確保玩家的資金安全。
豐富的遊戲選擇：從電子遊戲到真人娛樂，滿足各類玩家的需求。
專屬優惠：特別為Leo會員推出等級升等計畫，並提供多樣化的專屬活動。
快速出金：高效的財務系統，讓玩家的存取款過程快速無憂。
Leo會員轉移至富遊的流程
登錄富遊官網完成註冊。
提供Leo娛樂城會員等級截圖與相關資料（如戶名、手機號碼）給富遊客服進行審核。
等待客服確認後，享受富遊娛樂城專屬的會員福利與優惠。
結語：立即加入富遊娛樂城，延續遊戲體驗！
Leo娛樂城的退出讓許多玩家感到困惑與擔憂，但選擇穩定、安全的娛樂平台是最明智的應對之道。富遊娛樂城憑藉其卓越的技術、專業的服務以及豐富的優惠，成為玩家的理想替代選擇。現在就註冊富遊娛樂城，享受無與倫比的遊戲體驗吧！
九州娛樂城登入
Leo娛樂城無法登入？全面解析與解決指南
近期，Leo娛樂城的玩家紛紛反映登入失敗的情況，引發了廣泛的討論與擔憂。作為九州娛樂城旗下知名品牌之一，Leo娛樂城在台灣的娛樂市場中擁有大量用戶。然而，隨著九州娛樂城宣布將於2024年12月31日退出台灣市場，這一消息無疑讓玩家對資金安全與遊戲體驗產生了極大疑慮。
本文將深入探討Leo娛樂城無法登入的原因，提供解決方案，並推薦可靠的替代娛樂平台。
Leo娛樂城無法登入的三大原因
1. 帳號密碼問題
可能情況：最常見的原因是玩家輸入了錯誤的帳號或密碼，或者帳號被盜用。
解決方法：確認輸入的帳密正確，若仍無法登入，聯繫客服即可解決。
2. 網頁技術問題
可能情況：官網可能因伺服器維護或技術故障出現404錯誤，導致玩家無法登入。
解決方法：耐心等待官網修復，並清除瀏覽器快取和Cookie，或嘗試使用其他瀏覽器。
3. 九州娛樂城退出台灣市場
可能情況：隨著九州娛樂城宣布退出台灣市場，Leo娛樂城的營運也逐步停止，導致玩家無法再使用該平台。
影響：玩家可能面臨資金提取困難，需及時完成出金操作以保障自身利益。
娛樂城無法登入的緊急解決方案
核對帳號與密碼：確認輸入正確無誤，避免由於簡單疏忽造成的登入失敗。
檢查網路連線：確保網路穩定，必要時切換至更穩定的網路環境。
清除瀏覽器快取與Cookie：解決瀏覽器相關問題，恢復正常登入。
嘗試其他瀏覽器或設備：更換設備或使用不同瀏覽器，查看是否可以正常登入。
九州娛樂城退出台灣市場的原因
市場利潤有限：九州娛樂城認為台灣市場的競爭激烈且利潤有限，因此選擇退出並專注於其他海外市場。
資金生態鏈斷裂：現金交易平台出現問題，導致九州娛樂城難以維持正常運營。
母公司法律爭議：九州娛樂城母公司近年來因財務與法律問題受到高度關注，進一步影響旗下品牌的營運。
Leo娛樂城會員如何安全出金？
在九州娛樂城停止營運前，玩家需要立即完成出金操作以確保資金安全。
出金建議：
儘快登入官網提交提款申請，確保資金安全轉出。
若官網無法訪問，請嘗試聯繫客服，並保留交易證明以備進一步處理。
推薦替代平台：富遊娛樂城
隨著Leo娛樂城的退出，玩家可以考慮轉至穩定且值得信賴的替代平台，如富遊娛樂城。
富遊娛樂城的優勢
穩定可靠：擁有先進的技術和完善的資金保障機制，確保玩家的資金安全。
豐富的遊戲選擇：從電子遊戲到真人娛樂，滿足各類玩家的需求。
專屬優惠：特別為Leo會員推出等級升等計畫，並提供多樣化的專屬活動。
快速出金：高效的財務系統，讓玩家的存取款過程快速無憂。
Leo會員轉移至富遊的流程
登錄富遊官網完成註冊。
提供Leo娛樂城會員等級截圖與相關資料（如戶名、手機號碼）給富遊客服進行審核。
等待客服確認後，享受富遊娛樂城專屬的會員福利與優惠。
結語：立即加入富遊娛樂城，延續遊戲體驗！
Leo娛樂城的退出讓許多玩家感到困惑與擔憂，但選擇穩定、安全的娛樂平台是最明智的應對之道。富遊娛樂城憑藉其卓越的技術、專業的服務以及豐富的優惠，成為玩家的理想替代選擇。現在就註冊富遊娛樂城，享受無與倫比的遊戲體驗吧！
leo娛樂城
LEO娛樂城：九州娛樂集團的卓越創舉與運營優勢
九州娛樂集團總部的現代化運營
九州娛樂集團的總部設於菲律賓首都馬尼拉市中心最具代表性的現代化建築「RCBC Plaza」。這座辦公大樓融合了全球領先的建築科技與安全系統，包括：
國家級資訊防護系統，確保數據安全。
樓宇自動化系統 (BAS)，實現數位化管理與高效運營，包括防火系統、光纖電訊和數位監控。
九州娛樂為員工提供舒適的工作環境和專業的教育培訓，確保服務水準一流。其員工以專業知識和親切態度，為尊貴玩家帶來極致的遊戲體驗。
LEO娛樂旗下品牌與遊戲特色
九州娛樂城旗下分支包括 LEO、THA 和 KU 三個娛樂品牌。雖然品牌各自獨立運營，但都共享相同的遊戲系統與界面，提供超過數千款來自全球頂級供應商的遊戲。
這些品牌的核心特色包括：
種類繁多的遊戲：滿足不同類型玩家的需求，包括電子遊戲、體育博彩、真人娛樂等。
不斷更新的內容：通過九州獨家技術，網站內容保持新鮮，合作商可快速更新遊戲資源，確保平台競爭力。
玩家在這些平台上可以隨時找到適合自己的遊戲，享受沉浸式的娛樂體驗。
LEO娛樂城的歷史與發展
九州娛樂集團的起源可以追溯至其最早期的經營模式：「信用版」賭博平台 《天下體育球版》。儘管該模式在當時非常流行，但因高風險與財務處理複雜而逐漸被淘汰。
隨著市場需求的變化，九州娛樂轉型為現金版平台 《天下現金網》，引入了更安全、便捷的遊戲模式。這種轉變不僅提升了玩家的體驗，也使平台得以進一步發展。
如今，九州娛樂城已成為台灣博弈業界的領軍者，不僅優化了網站版面與功能，還推出了專屬手機APP，方便玩家隨時隨地進行遊戲體驗。
LEO娛樂的成功秘訣
現代化運營與技術支持：九州娛樂在系統安全與技術更新方面投入巨大資源，確保平台運營穩定可靠。
多元化遊戲體驗：通過與全球頂級遊戲供應商合作，平台提供了豐富的遊戲選擇，適應各種玩家需求。
用戶至上：專業培訓的員工以細心和熱忱態度，提供高品質服務，讓玩家倍感尊重。
不斷創新：從信用版到現金版，再到手機APP，九州娛樂始終緊跟市場趨勢，致力於打造最佳娛樂體驗。
結語
LEO娛樂城作為九州娛樂集團旗下的重要品牌，不僅繼承了集團的核心價值，更在遊戲選擇、服務品質和技術創新方面不斷提升。從最初的《天下體育球版》到如今的行業領先者，LEO娛樂見證了九州娛樂城的發展歷程，也成為博弈行業中的耀眼明星。
加入 LEO娛樂城，感受來自九州娛樂集團的專業與熱情，享受最頂級的線上博弈體驗！
Leo娛樂城無法登入？全面解析與解決指南
近期，Leo娛樂城的玩家紛紛反映登入失敗的情況，引發了廣泛的討論與擔憂。作為九州娛樂城旗下知名品牌之一，Leo娛樂城在台灣的娛樂市場中擁有大量用戶。然而，隨著九州娛樂城宣布將於2024年12月31日退出台灣市場，這一消息無疑讓玩家對資金安全與遊戲體驗產生了極大疑慮。
本文將深入探討Leo娛樂城無法登入的原因，提供解決方案，並推薦可靠的替代娛樂平台。
Leo娛樂城無法登入的三大原因
1. 帳號密碼問題
可能情況：最常見的原因是玩家輸入了錯誤的帳號或密碼，或者帳號被盜用。
解決方法：確認輸入的帳密正確，若仍無法登入，聯繫客服即可解決。
2. 網頁技術問題
可能情況：官網可能因伺服器維護或技術故障出現404錯誤，導致玩家無法登入。
解決方法：耐心等待官網修復，並清除瀏覽器快取和Cookie，或嘗試使用其他瀏覽器。
3. 九州娛樂城退出台灣市場
可能情況：隨著九州娛樂城宣布退出台灣市場，Leo娛樂城的營運也逐步停止，導致玩家無法再使用該平台。
影響：玩家可能面臨資金提取困難，需及時完成出金操作以保障自身利益。
娛樂城無法登入的緊急解決方案
核對帳號與密碼：確認輸入正確無誤，避免由於簡單疏忽造成的登入失敗。
檢查網路連線：確保網路穩定，必要時切換至更穩定的網路環境。
清除瀏覽器快取與Cookie：解決瀏覽器相關問題，恢復正常登入。
嘗試其他瀏覽器或設備：更換設備或使用不同瀏覽器，查看是否可以正常登入。
九州娛樂城退出台灣市場的原因
市場利潤有限：九州娛樂城認為台灣市場的競爭激烈且利潤有限，因此選擇退出並專注於其他海外市場。
資金生態鏈斷裂：現金交易平台出現問題，導致九州娛樂城難以維持正常運營。
母公司法律爭議：九州娛樂城母公司近年來因財務與法律問題受到高度關注，進一步影響旗下品牌的營運。
Leo娛樂城會員如何安全出金？
在九州娛樂城停止營運前，玩家需要立即完成出金操作以確保資金安全。
出金建議：
儘快登入官網提交提款申請，確保資金安全轉出。
若官網無法訪問，請嘗試聯繫客服，並保留交易證明以備進一步處理。
推薦替代平台：富遊娛樂城
隨著Leo娛樂城的退出，玩家可以考慮轉至穩定且值得信賴的替代平台，如富遊娛樂城。
富遊娛樂城的優勢
穩定可靠：擁有先進的技術和完善的資金保障機制，確保玩家的資金安全。
豐富的遊戲選擇：從電子遊戲到真人娛樂，滿足各類玩家的需求。
專屬優惠：特別為Leo會員推出等級升等計畫，並提供多樣化的專屬活動。
快速出金：高效的財務系統，讓玩家的存取款過程快速無憂。
Leo會員轉移至富遊的流程
登錄富遊官網完成註冊。
提供Leo娛樂城會員等級截圖與相關資料（如戶名、手機號碼）給富遊客服進行審核。
等待客服確認後，享受富遊娛樂城專屬的會員福利與優惠。
結語：立即加入富遊娛樂城，延續遊戲體驗！
Leo娛樂城的退出讓許多玩家感到困惑與擔憂，但選擇穩定、安全的娛樂平台是最明智的應對之道。富遊娛樂城憑藉其卓越的技術、專業的服務以及豐富的優惠，成為玩家的理想替代選擇。現在就註冊富遊娛樂城，享受無與倫比的遊戲體驗吧！
想要享受最刺激的線上娛樂體驗？選擇RG富遊娛樂城！
在這個數位時代，尋找適合自己的線上娛樂城變得越來越重要。如果你想在線上娛樂城找到最好玩、最受歡迎的遊戲，RG富遊絕對是你的首選！我們匯聚了多款博弈遊戲，讓您盡情享受娛樂的刺激與快感。
#### 精選遊戲類型
1. 真人百家樂
感受現場賭場的氛圍！RG富遊的真人視訊百家樂讓你與真實的荷官互動，享受高品質的遊戲體驗。無論你是老手還是新手，都能在這裡找到適合自己的節奏。
2. 電子老虎機
喜愛刺激嗎？我們提供多款熱門老虎機遊戲，如「戰神賽特」「魔龍傳奇」等，每一款都擁有精美的畫面和豐厚的獎勵，讓每次旋轉都充滿期待！
3. 體育投注
無論你是球迷還是賽事愛好者，RG富遊的體育投注平台都有你想要的。精準的賠率、廣泛的賽事選擇，讓你體驗到投注的樂趣和刺激。
4. 彩票遊戲與捕魚遊戲
隨著運氣來！不妨試試我們的棋牌遊戲和彩票遊戲，這裡有各種機會讓你體驗到不一樣的勝利快感。
#### 下載富遊APP，隨時隨地享受遊戲！
富遊娛樂城的APP支持iOS和Android設備，界面簡潔易用，內容豐富。無論你身處何地，都能輕鬆進入遊戲世界，隨心所欲享受娛樂時光。此外，我們提供即時客服支援，隨時解決你的疑問，讓你的遊戲體驗更為完美。
#### 為什麼選擇RG富遊？
– 安全可靠
RG富遊致力於為玩家提供安全可靠的遊戲環境，您的每一筆交易都受到最高的安全保障。
– 快速便捷的存提款服務
我們的存款平均時間僅需30秒，提款平均只需60秒，讓你體驗即時的快感！
– 豐富多元的遊戲選擇
超過9999款遊戲任你選擇，無論你偏好哪種娛樂方式，這裡都能滿足你的需求。
– 全天候服務
我們全年365天提供不停歇的客服支持，確保你在遊戲過程中享受到最好的服務。
### 結論
RG富遊娛樂城是您最佳的線上賭場選擇。我們不僅提供多樣化的遊戲選擇，還有安全可靠的遊戲環境和便捷的服務。立即下載APP，加入RG富遊，開始您的娛樂之旅，享受無與倫比的遊戲體驗吧！
滿天星娛樂城：全方位的線上娛樂體驗
滿天星娛樂城作為九州娛樂城旗下品牌之一，是玩家心目中備受信賴的線上娛樂平台。不僅提供豐富的遊戲選擇和吸引人的優惠，還以其合法營運的背景和快速出金的保證，成為台灣玩家的首選娛樂城之一。
滿天星娛樂城的特色與優勢
1. 合法營運，安全可靠
滿天星娛樂城持有三大國際娛樂執照，包括：
菲律賓 PAGCOR 監督競猜牌照
BVI 認證
馬爾他 MGA 認證
這些執照展現了平台的資本實力與合法性，讓玩家能夠安心享受遊戲，完全不用擔心出金問題。
2. 高品質遊戲與豐富優惠
滿天星娛樂城與九州集團旗下的LEO、THA娛樂城一樣，提供一流的遊戲品質和多樣化的優惠。
熱門遊戲推薦：電子老虎機、真人直播、運彩投注、今彩539等，滿足各類玩家需求。
優惠活動：定期推出限時回饋活動，讓玩家在遊戲中獲得更多額外收益。
3. 快速出金與高效服務
滿天星娛樂城採用先進的財務系統，確保存提款快速、安全，讓玩家能夠專注於享受遊戲，而無需擔心資金問題。專業的客服團隊24小時在線，提供即時支援。
4. 多平台兼容的APP
滿天星娛樂城提供設計貼合玩家需求的手機APP，適用於iOS與Android系統。玩家可以隨時隨地快速登入遊玩，體驗無與倫比的娛樂快感。
熱門遊戲類型一覽
滿天星娛樂城為玩家提供多樣化的遊戲選擇，滿足不同興趣和需求：
真人直播：感受真實賭場氛圍，與真人荷官互動，體驗沉浸式娛樂。
電子老虎機：多款經典與創新機台，讓玩家享受刺激的遊戲過程。
運彩投注：涵蓋世界盃、棒球、籃球等多項運動賽事，提供即時投注與直播功能。
彩票遊戲：包括今彩539、富遊彩票等，適合熱衷於彩券的玩家。
滿天星娛樂城常見問題解答
Q1. 滿天星娛樂城是否提供APP下載？
是的，滿天星娛樂城提供專屬的手機APP，支援iOS和Android系統。玩家可透過APP快速登入，隨時享受遊戲。
Q2. 滿天星娛樂城是否合法？
滿天星娛樂城擁有多項國際認證，為合法經營的線上娛樂城，並保證玩家資金的安全性與遊戲的公平性。
Q3. 無法登入滿天星娛樂城該怎麼辦？
如遇到無法登入的情況，建議玩家檢查網路狀況或聯繫24小時客服團隊獲取即時協助。
立即加入滿天星娛樂城，享受最佳娛樂體驗！
滿天星娛樂城以合法、安全、快速的服務，搭配豐富的遊戲選擇和優惠，為玩家打造出獨一無二的線上娛樂體驗。不論您是新手還是老手，都能在滿天星找到屬於自己的遊戲樂趣。現在就下載APP，隨時隨地開始您的娛樂之旅！
Как официально купить диплом вуза с упрощенным обучением в Москве
娛樂城
富遊娛樂城：台灣線上賭場的創新選擇
在台灣的線上娛樂市場中，富遊娛樂城憑藉其優質的服務和多樣化的娛樂選項，迅速成為新一代玩家的首選。既有刺激的遊戲體驗，又提供了一系列具有吸引力的優惠，富遊娛樂城無疑是追求樂趣的玩家們理想的地方。
#### 優勢與特色
1. 多樣化的遊戲選擇
富遊娛樂城提供了豐富的遊戲種類，包括電子老虎機、真人百家樂、運彩投注等。不論你是老虎機的愛好者，還是熱衷於真人賭桌的玩家，這裡都能滿足你的需求。特別推薦的遊戲如DG真人百家和RSG皇家百家樂，一定能帶給你極致的遊戲體驗。
2. 吸引人的優惠活動
富遊娛樂城針對新手和老玩家都推出了多樣的優惠活動。新會員首次存款可獲得相同金額的獎金，還有額外的體驗金送出，設計友好且實惠。此外，富遊每週的簽到獎勵和天天無上限的返水活動，更是讓玩家在遊戲中能持續獲得收益。
3. 安全可靠的存取款方式
在金融交易方面，富遊娛樂城支持多種存款和提款方式，包括各大銀行轉帳、超商儲值，甚至虛擬貨幣等。最低提款金額設置靈活，保證玩家資金的安全與便捷。
4. 人性化的操作介面
富遊娛樂城的網頁與移動應用設計簡潔易用，玩家可以方便地找到所需的遊戲和優惠。無論是在電腦還是手機上，都能順利享受到遊戲的樂趣。
#### 如何開始遊戲
如果你是新手玩家，開始你的富遊體驗非常簡單。只需註冊帳號，完成首次存款，即可獲得新手優惠。無論你想嘗試電子遊戲還是真人賭局，富遊娛樂城都能讓你輕鬆上手，享受娛樂的樂趣。
#### 社會責任與防沉迷措施
富遊娛樂城深知線上賭博的風險，因此致力於推廣負責任的遊戲文化。他們提供“防沉迷”指導，以確保玩家能夠理性投注，並提供必要的幫助和資源來幫助有需求的玩家。
#### 總結
對於尋求安全、便捷和多元化娛樂城體驗的玩家，富遊娛樂城絕對是值得選擇的選項。無論你是希望徹底放鬆，還是想要體驗刺激的博弈過程，富遊娛樂城都能滿足你的期待，成為你在台灣線上娛樂市場的最佳夥伴。立即註冊並開始你的遊戲之旅吧！
LEO娛樂城無法登入！九州娛樂宣布退出台灣市場
近期，LEO娛樂城和THA娛樂城的玩家發現頻繁出現無法登入的情況，引發了廣泛討論。九州娛樂城官方也正式宣布，將於2024年12月31日中午12:00停止在台灣的營運，並結束所有相關服務。這一消息對於忠實玩家來說無疑是一大震撼，為什麼九州娛樂城會退出台灣市場？玩家該如何應對？本文將為您逐一解析。
LEO娛樂城無法登入的原因
1. 帳號與密碼問題
最常見的情況是玩家輸入的帳號或密碼有誤，或者帳號遭到盜用。
解決方案：聯繫LEO娛樂城的客服，提供必要的驗證信息，即可快速恢復帳戶。
2. 網站技術故障
LEO娛樂城可能因官網維護或伺服器異常導致無法正常運作。
解決方案：耐心等待技術問題修復，通常不會影響長時間使用。
3. 九州娛樂退出台灣市場
LEO娛樂城隸屬於九州娛樂集團，近期官方公告將於2024年12月31日結束營運，退出台灣市場。這是導致登入失敗的最終原因，玩家將無法再使用該平台的服務。
九州娛樂城退出台灣市場的原因分析
1. 市場規模限制
九州娛樂認為台灣市場過於狹小，品牌競爭激烈，成長空間有限。相比之下，海外市場不僅擁有更大的人口基數，也提供更高的獲利潛力。九州旗下的KU體育曾在國際足球五大聯賽中曝光，這顯示其具備強大的國際競爭力，轉向海外市場發展成為合理選擇。
2. 金流問題與法規壓力
LEO娛樂城的運營高度依賴第三方金流公司，而近期陳政谷案件的爆發使整個金流生態鏈受到嚴重打擊。警方揭露，九州娛樂集團利用第三方支付進行資金洗錢，甚至牽涉到內部人員洩密，對整個集團的形象和運營造成巨大衝擊。
3. 品牌聲譽受損
隨著案件的曝光，九州娛樂集團的聲譽遭到前所未有的挑戰。為了平息風波，九州選擇退出台灣市場，以避免進一步的法律與政策風險。
九州娛樂城停止營運的公告
根據LEO娛樂城官方的公告，九州娛樂城將於2024年12月31日中午12:00全面停止台灣市場的營運：
停止存款功能：玩家將無法再進行任何存款操作。
正常開放提款：官方承諾保證提款功能正常運作，會員可安心提取資金。
感謝支持：九州娛樂對於玩家多年來的支持表示衷心感謝，並祝福所有會員未來一切順利。
玩家應對策略：如何保護自身利益？
1. 儘速完成提款
如您的帳戶仍可正常登入，建議立即提交提款申請，確保資金安全轉出。
2. 提高警覺，避免詐騙
隨著九州娛樂退出，市場可能會出現冒充LEO娛樂城或THA娛樂城的假冒平台，玩家需保持高度警覺。
3. 選擇可靠的替代平台
對於希望延續遊戲體驗的玩家，可以考慮轉向信譽良好的國際娛樂平台，例如Bet365台灣，該平台提供穩定的服務和多樣化的遊戲選擇，是九州娛樂的理想替代方案。
結語：九州娛樂的結束，玩家的新起點
九州娛樂城的退出標誌著一個時代的結束，但對於玩家而言，也是一個選擇新平台的契機。未來，選擇安全、穩定且合法的娛樂平台將成為玩家的首要考量。無論如何，希望所有玩家都能在新的平台中繼續享受遊戲的樂趣，保障自身利益不受損失！
Сколько стоит получить диплом высшего и среднего образования легально?
капельница от похмелья на дому цена капельница от похмелья на дому цена .
снятие запоя на дому снятие запоя на дому .
капельница от запоя капельница от запоя .
капельница от запоя вызов капельница от запоя вызов .
капельница на дому круглосуточно капельница на дому круглосуточно .
Купить диплом в России, предлагает наша компания
Собственное производство металлоконструкций. Если вас интересует навес для машин на даче мы предлогаем изготовление под ключ Навесы для дачи арочные
LEO娛樂城無法登入
九州娛樂城退出台灣市場：LEO娛樂城無法登入的背後真相
LEO娛樂城，作為台灣線上娛樂城市場的重要品牌，長期以來在廣告投放和代理推廣方面占據領先地位。然而，近期出現的「LEO娛樂城無法登入」現象引發了廣泛的網路討論。不少玩家質疑：「九州娛樂城是不是倒了？」「這是不是詐騙？」事實上，這些猜測與謠言並不完全準確。根據最新消息，九州娛樂城已決定結束其在台灣的業務，包括旗下品牌LEO娛樂城和THA娛樂城。以下我們將深入分析這一事件的背景和可能的影響。
LEO娛樂城無法登入的原因分析
近期LEO娛樂城頻繁出現無法登入的情況，其實是九州娛樂城退出台灣市場的前兆。根據官方公告，九州娛樂城將於2024年12月31日中午12點正式關閉，包括註冊與存款功能在內的多項服務已經受到限制。
可能原因 1：退出台灣市場的策略
九州娛樂城的管理層認為，台灣市場的利潤已達上限，長期運營的收益減少，因此選擇「見好就收」。這一策略符合台灣商業文化中尋找新市場發展的特點。九州娛樂城可能計劃將資源投入其他更具潛力的市場，以追求更大的收益。
可能原因 2：運營生態鏈的問題
LEO娛樂城的運營高度依賴第三方現金交易平台以及相關支付管道。近期，這些環節可能出現了無法解決的問題，導致整體運營受阻。為了避免損失擴大，九州娛樂城選擇退出台灣市場。
可能原因 3：法律風險與負面新聞
九州娛樂城因涉及法律事件，曾多次登上新聞版面。這些事件不僅損害了品牌形象，也讓經營面臨更多風險。為了降低法律糾紛帶來的影響，九州娛樂城可能選擇結束在台灣的營運。
官方公告：2024年12月31日正式停業
九州娛樂城已向所有LEO娛樂城會員發布公告，明確指出將於2024年12月31日中午12點全面停止營運。公告內容包括以下重要信息：
存款服務已關閉：玩家無法繼續充值。
提款功能仍正常：玩家可以放心提取餘額，會員權益不受影響。
感謝支持：官方對會員表達了感謝，並祝福大家未來順利。
這一公告讓玩家可以在剩餘時間內完成提款操作，避免資金損失。
對玩家的影響與建議
1. 儘快提款
如果您是LEO娛樂城的會員，應立即登入帳戶並提取餘額，以確保資金安全。
2. 謹慎選擇新平台
選擇新的娛樂平台時，應注意以下幾點：
合法性：確認平台是否擁有合法經營許可。
支付系統穩定性：確保提款及充值渠道安全無虞。
用戶評價：參考其他玩家的反饋，選擇口碑良好的平台。
3. 防範詐騙
警惕假冒的LEO娛樂城網站或客服。官方客服系統已關閉，任何聯繫您索取個人資料的行為都可能是詐騙。
結語
LEO娛樂城無法登入以及九州娛樂城退出台灣市場，標誌著線上娛樂城行業的一次重要轉折。對於玩家而言，這既是一個挑戰，也是一個重新審視平台選擇的機會。未來，玩家應更加關注平台的合法性與穩定性，為自己的遊戲體驗和資金安全提供保障。
Где и как купить диплом о высшем образовании без лишних рисков
Тактичные штаны: идеальный выбор для стильных мужчин, как носить их с другой одеждой.
Неотъемлемая часть гардероба – тактичные штаны, которые подчеркнут ваш стиль и индивидуальность.
Идеальные тактичные штаны: находка для занятых людей, который подчеркнет вашу уверенность и статус.
Лучшие модели тактичных штанов для мужчин, которые подчеркнут вашу спортивную натуру.
Советы по выбору тактичных штанов для мужчин, чтобы подчеркнуть свою уникальность и индивидуальность.
Секрет стильных мужчин: тактичные штаны, которые подчеркнут ваш вкус и качество вашей одежды.
Сочетание стиля и практичности в тактичных штанах, которые подчеркнут ваш профессионализм и серьезность.
купити штани олива тактичні https://dffrgrgrgdhajshf.com.ua/ .
冠天下娛樂城
2024 年熱門娛樂城與活動解析
冠天下娛樂城優惠，帶來無限樂趣
在 2024 年 4 月 16 日，冠天下娛樂城推出了全新的優惠活動，旨在為玩家帶來更大的獲利機會和更高的娛樂體驗。這些優惠活動包括多種存款獎勵、會員專屬回饋以及豐富的遊戲競賽獎金，吸引了大批玩家參與。
冠天下娛樂城以其高透明度和用戶友好的政策，已成為許多玩家的首選娛樂平台。不論是新手還是老手，都能在這裡找到適合自己的遊戲和活動。
LEO娛樂城無法登入引發市場恐慌
2024 年 11 月 29 日，LEO娛樂城因技術問題出現短暫無法登入的情況，引發了廣泛關注。許多玩家擔心這是否意味著九州娛樂城的營運出現問題。
九州娛樂集團隨後發佈官方聲明，強調這僅僅是系統升級過程中的短暫問題，並承諾玩家的資金和數據安全不受任何影響。同時，九州娛樂表示將加強伺服器穩定性，確保未來類似情況不再發生。
熱門 ZG 電子遊戲——熱舞森巴老虎機
2024 年 11 月 8 日，ZG 電子遊戲推出了熱舞森巴老虎機，這款遊戲迅速成為市場上的熱門選擇。以南美熱情的森巴舞為主題，遊戲畫面充滿色彩，搭配動感的音樂，為玩家帶來視覺與聽覺的雙重享受。
遊戲亮點：
高倍數獎勵機制：每次轉盤都有機會觸發高額獎金。
特色免費遊戲：連續獲得特殊圖案即可啟動多次免費轉盤，提高獲勝機率。
適合新手與高端玩家：簡單的玩法規則與豐富的策略選擇滿足不同層級玩家的需求。
ZG 電子遊戲致力於為玩家提供創新且有趣的遊戲體驗，熱舞森巴老虎機無疑是今年最值得嘗試的遊戲之一。
2024 世界棒球 12 強賽精彩回顧
2024 年 11 月，中華隊參加了世界棒球 12 強賽，這項全球頂尖棒球賽事吸引了來自多國的球隊和球迷參與。中華隊 28 人的名單以年輕選手和經驗豐富的老將為基礎，展現了團隊的競技實力。
比賽亮點：
精彩賽程：比賽期間，中華隊展現了堅強的防守和出色的打擊表現。
門票銷售：賽事門票迅速售罄，顯示出棒球在台灣的高度受歡迎程度。
線上直播：各大平台提供了高畫質直播，讓更多球迷能夠即時觀看比賽，感受棒球魅力。
世界棒球 12 強賽不僅是比賽，更是全台灣球迷的一場盛宴，展現了棒球作為國民運動的無限魅力。
結語
從娛樂城的優惠活動到全球性的棒球賽事，2024 年對於遊戲和體育愛好者來說充滿了亮點。不論是參與冠天下娛樂城的優惠，體驗 ZG 電子遊戲的最新老虎機，還是為中華隊的棒球比賽加油，這一年都是充滿精彩與期待的一年！
Официальная покупка школьного аттестата с упрощенным обучением в Москве
Официальная покупка аттестата о среднем образовании в Москве и других городах
врач на дом капельница от запоя врач на дом капельница от запоя .
капельница от запоя вызов на дом капельница от запоя вызов на дом .
капельница при алкогольной интоксикации на дому цена капельница при алкогольной интоксикации на дому цена .
valif pills hut – buy sustiva medication buy sinemet 10mg sale
Официальная покупка диплома вуза с упрощенной программой обучения
врач на дом капельница от запоя врач на дом капельница от запоя .
Как оказалось, купить диплом кандидата наук не так уж и сложно
娛樂城
2024 年娛樂城遊戲推薦：最夯遊戲與最佳平台選擇
隨著線上娛樂城市場的蓬勃發展，2024 年推出了多款令人興奮的遊戲和創新平台。無論是喜歡老虎機、棋牌遊戲，還是捕魚和彩票遊戲的玩家，都能在今年找到屬於自己的遊戲樂園。以下是熱門遊戲推薦與最佳娛樂城平台的詳細介紹。
2024 年最夯遊戲推薦
電子老虎機遊戲
電子老虎機一直是娛樂城的經典項目，今年更是推出了數款熱門作品：
戰神賽特：以古埃及神話為背景，擁有高倍數獎勵的特殊功能，畫面設計精美。
魔龍傳奇：玩家可探索魔龍世界，觸發驚喜獎金和免費遊戲機會。
雷神之錘：以北歐神話為主題，特色連線玩法讓每次旋轉都充滿期待。
金虎爺：寓意招財進寶，特別適合新年期間挑戰，玩法簡單但回報豐厚。
棋牌遊戲
二人麻將：適合喜歡策略性對抗的玩家，快速節奏且競爭激烈。
忍 Kunoichi：結合武士與忍者元素，讓玩家體驗獨特的棋牌競技。
捕魚遊戲
捕魚遊戲是一種結合策略和運氣的娛樂項目，玩家可以通過捕捉魚群來獲得高額獎金，同時享受視覺和操作的雙重樂趣。
彩票遊戲
彩票遊戲以簡單快捷的玩法吸引大批玩家，提供多種國內外彩種，讓玩家隨時挑戰幸運。
RG富遊娛樂城：2024 年最佳線上娛樂城推薦
在眾多娛樂城平台中，RG富遊娛樂城以其專業服務和卓越遊戲體驗，成為今年的首選平台。
平台特色
遊戲種類豐富
提供多元化遊戲選擇，包括真人視訊、電子老虎機、捕魚、棋牌和彩票遊戲，滿足所有玩家需求。
快速便捷的存提款服務
平台支持即時存款與快速提款，無需等待，確保資金安全流動。
高度安全保障
採用最先進的加密技術，保護玩家的帳戶與交易安全。
支援多平台裝置
富遊娛樂城APP 可在 iOS 和 Android 設備上使用，界面簡潔易操作，隨時隨地享受娛樂。
專業客服支援
提供 24 小時全天候客服，隨時解答玩家疑問，保障流暢的遊戲體驗。
如何開始體驗 RG 富遊娛樂城
下載富遊 APP
在官方網站免費下載 APP，支援 iOS 和 Android 設備。
註冊帳號
使用簡單步驟完成註冊，立即進入遊戲世界。
挑戰熱門遊戲
從老虎機到棋牌遊戲，選擇您喜歡的類型，挑戰高額獎金。
結語
2024 年是線上娛樂遊戲的精彩年份，從戰神賽特到二人麻將，每款遊戲都能帶給玩家不同的樂趣。而選擇像 RG富遊娛樂城 這樣的專業平台，不僅能體驗到豐富的遊戲內容，還能享受安全可靠的服務。立即下載富遊 APP，加入這個充滿驚喜的娛樂世界
Реально ли приобрести диплом стоматолога? Основные этапы
Тут можно преобрести cейфы взломостойкие взломостойкие сейфы цена
滿天星娛樂城
滿天星娛樂城：全方位的線上娛樂體驗
滿天星娛樂城作為九州娛樂城旗下品牌之一，是玩家心目中備受信賴的線上娛樂平台。不僅提供豐富的遊戲選擇和吸引人的優惠，還以其合法營運的背景和快速出金的保證，成為台灣玩家的首選娛樂城之一。
滿天星娛樂城的特色與優勢
1. 合法營運，安全可靠
滿天星娛樂城持有三大國際娛樂執照，包括：
菲律賓 PAGCOR 監督競猜牌照
BVI 認證
馬爾他 MGA 認證
這些執照展現了平台的資本實力與合法性，讓玩家能夠安心享受遊戲，完全不用擔心出金問題。
2. 高品質遊戲與豐富優惠
滿天星娛樂城與九州集團旗下的LEO、THA娛樂城一樣，提供一流的遊戲品質和多樣化的優惠。
熱門遊戲推薦：電子老虎機、真人直播、運彩投注、今彩539等，滿足各類玩家需求。
優惠活動：定期推出限時回饋活動，讓玩家在遊戲中獲得更多額外收益。
3. 快速出金與高效服務
滿天星娛樂城採用先進的財務系統，確保存提款快速、安全，讓玩家能夠專注於享受遊戲，而無需擔心資金問題。專業的客服團隊24小時在線，提供即時支援。
4. 多平台兼容的APP
滿天星娛樂城提供設計貼合玩家需求的手機APP，適用於iOS與Android系統。玩家可以隨時隨地快速登入遊玩，體驗無與倫比的娛樂快感。
熱門遊戲類型一覽
滿天星娛樂城為玩家提供多樣化的遊戲選擇，滿足不同興趣和需求：
真人直播：感受真實賭場氛圍，與真人荷官互動，體驗沉浸式娛樂。
電子老虎機：多款經典與創新機台，讓玩家享受刺激的遊戲過程。
運彩投注：涵蓋世界盃、棒球、籃球等多項運動賽事，提供即時投注與直播功能。
彩票遊戲：包括今彩539、富遊彩票等，適合熱衷於彩券的玩家。
滿天星娛樂城常見問題解答
Q1. 滿天星娛樂城是否提供APP下載？
是的，滿天星娛樂城提供專屬的手機APP，支援iOS和Android系統。玩家可透過APP快速登入，隨時享受遊戲。
Q2. 滿天星娛樂城是否合法？
滿天星娛樂城擁有多項國際認證，為合法經營的線上娛樂城，並保證玩家資金的安全性與遊戲的公平性。
Q3. 無法登入滿天星娛樂城該怎麼辦？
如遇到無法登入的情況，建議玩家檢查網路狀況或聯繫24小時客服團隊獲取即時協助。
立即加入滿天星娛樂城，享受最佳娛樂體驗！
滿天星娛樂城以合法、安全、快速的服務，搭配豐富的遊戲選擇和優惠，為玩家打造出獨一無二的線上娛樂體驗。不論您是新手還是老手，都能在滿天星找到屬於自己的遊戲樂趣。現在就下載APP，隨時隨地開始您的娛樂之旅！
Официальная покупка диплома вуза с сокращенной программой в Москве
娛樂城
富遊娛樂城：台灣線上賭場的創新選擇
在台灣的線上娛樂市場中，富遊娛樂城憑藉其優質的服務和多樣化的娛樂選項，迅速成為新一代玩家的首選。既有刺激的遊戲體驗，又提供了一系列具有吸引力的優惠，富遊娛樂城無疑是追求樂趣的玩家們理想的地方。
#### 優勢與特色
1. 多樣化的遊戲選擇
富遊娛樂城提供了豐富的遊戲種類，包括電子老虎機、真人百家樂、運彩投注等。不論你是老虎機的愛好者，還是熱衷於真人賭桌的玩家，這裡都能滿足你的需求。特別推薦的遊戲如DG真人百家和RSG皇家百家樂，一定能帶給你極致的遊戲體驗。
2. 吸引人的優惠活動
富遊娛樂城針對新手和老玩家都推出了多樣的優惠活動。新會員首次存款可獲得相同金額的獎金，還有額外的體驗金送出，設計友好且實惠。此外，富遊每週的簽到獎勵和天天無上限的返水活動，更是讓玩家在遊戲中能持續獲得收益。
3. 安全可靠的存取款方式
在金融交易方面，富遊娛樂城支持多種存款和提款方式，包括各大銀行轉帳、超商儲值，甚至虛擬貨幣等。最低提款金額設置靈活，保證玩家資金的安全與便捷。
4. 人性化的操作介面
富遊娛樂城的網頁與移動應用設計簡潔易用，玩家可以方便地找到所需的遊戲和優惠。無論是在電腦還是手機上，都能順利享受到遊戲的樂趣。
#### 如何開始遊戲
如果你是新手玩家，開始你的富遊體驗非常簡單。只需註冊帳號，完成首次存款，即可獲得新手優惠。無論你想嘗試電子遊戲還是真人賭局，富遊娛樂城都能讓你輕鬆上手，享受娛樂的樂趣。
#### 社會責任與防沉迷措施
富遊娛樂城深知線上賭博的風險，因此致力於推廣負責任的遊戲文化。他們提供“防沉迷”指導，以確保玩家能夠理性投注，並提供必要的幫助和資源來幫助有需求的玩家。
#### 總結
對於尋求安全、便捷和多元化娛樂城體驗的玩家，富遊娛樂城絕對是值得選擇的選項。無論你是希望徹底放鬆，還是想要體驗刺激的博弈過程，富遊娛樂城都能滿足你的期待，成為你在台灣線上娛樂市場的最佳夥伴。立即註冊並開始你的遊戲之旅吧！
想要享受最刺激的線上娛樂體驗？選擇RG富遊娛樂城！
在這個數位時代，尋找適合自己的線上娛樂城變得越來越重要。如果你想在線上娛樂城找到最好玩、最受歡迎的遊戲，RG富遊絕對是你的首選！我們匯聚了多款博弈遊戲，讓您盡情享受娛樂的刺激與快感。
#### 精選遊戲類型
1. 真人百家樂
感受現場賭場的氛圍！RG富遊的真人視訊百家樂讓你與真實的荷官互動，享受高品質的遊戲體驗。無論你是老手還是新手，都能在這裡找到適合自己的節奏。
2. 電子老虎機
喜愛刺激嗎？我們提供多款熱門老虎機遊戲，如「戰神賽特」「魔龍傳奇」等，每一款都擁有精美的畫面和豐厚的獎勵，讓每次旋轉都充滿期待！
3. 體育投注
無論你是球迷還是賽事愛好者，RG富遊的體育投注平台都有你想要的。精準的賠率、廣泛的賽事選擇，讓你體驗到投注的樂趣和刺激。
4. 彩票遊戲與捕魚遊戲
隨著運氣來！不妨試試我們的棋牌遊戲和彩票遊戲，這裡有各種機會讓你體驗到不一樣的勝利快感。
#### 下載富遊APP，隨時隨地享受遊戲！
富遊娛樂城的APP支持iOS和Android設備，界面簡潔易用，內容豐富。無論你身處何地，都能輕鬆進入遊戲世界，隨心所欲享受娛樂時光。此外，我們提供即時客服支援，隨時解決你的疑問，讓你的遊戲體驗更為完美。
#### 為什麼選擇RG富遊？
– 安全可靠
RG富遊致力於為玩家提供安全可靠的遊戲環境，您的每一筆交易都受到最高的安全保障。
– 快速便捷的存提款服務
我們的存款平均時間僅需30秒，提款平均只需60秒，讓你體驗即時的快感！
– 豐富多元的遊戲選擇
超過9999款遊戲任你選擇，無論你偏好哪種娛樂方式，這裡都能滿足你的需求。
– 全天候服務
我們全年365天提供不停歇的客服支持，確保你在遊戲過程中享受到最好的服務。
### 結論
RG富遊娛樂城是您最佳的線上賭場選擇。我們不僅提供多樣化的遊戲選擇，還有安全可靠的遊戲環境和便捷的服務。立即下載APP，加入RG富遊，開始您的娛樂之旅，享受無與倫比的遊戲體驗吧！
Купить диплом в России, предлагает наша компания
капельница от запоя на дому нижний новгород капельница от запоя на дому нижний новгород .
3A娛樂城
3A娛樂城：全方位線上娛樂體驗的首選平台
3A娛樂城作為台灣最受歡迎的線上娛樂平台之一，以其多樣化的遊戲選擇、創新的技術、以及卓越的安全保障，贏得了玩家的高度信任與青睞。無論您是新手還是老手，3A娛樂城都能滿足您的需求，帶給您獨一無二的遊戲體驗。
熱門娛樂城遊戲一覽
3A娛樂城提供多種熱門遊戲，適合不同類型的玩家：
真人百家樂：體驗真實賭場的氛圍，與真人荷官互動，感受賭桌上的緊張與刺激。
彩票投注：涵蓋多種彩票選項，滿足彩券愛好者的需求，讓您隨時隨地挑戰幸運。
棋牌遊戲：從傳統的麻將到現代化的紙牌遊戲，讓玩家在策略與運氣中找到平衡。
3A娛樂城的核心價值
1. 專業
3A娛樂城每日提供近千場體育賽事，並搭配真人百家樂、彩票彩球、電子遊戲等多種類型的線上賭場遊戲。無論您的遊戲偏好為何，這裡總有一款適合您！
2. 安全
平台採用128位加密技術和嚴格的安全管理體系，確保玩家的金流與個人資料完全受保護，讓您可以放心遊玩，無需擔憂安全問題。
3. 便捷
3A娛樂城是全台第一家使用自家開發的全套終端應用的娛樂城平台。無論是手機還是電腦，玩家都能享受無縫的遊戲體驗。同時，24小時線上客服隨時為您解決任何問題，提供貼心服務。
4. 安心
由專業工程師開發的財務處理系統，為玩家帶來快速的存款、取款和轉帳服務。透過獨立網路技術，平台提供優化的網路速度，確保每一次操作都流暢無比。
下載3A娛樂城手機APP
為了提供更便捷的遊戲體驗，3A娛樂城獨家開發了功能齊全的手機APP，讓玩家隨時隨地開啟遊戲。
現代化設計：新穎乾淨的介面設計，提升使用者體驗。
跨平台支持：完美適配手機與電腦，讓您輕鬆切換設備，無需中斷遊戲。
快速下載：掃描專屬QR碼即可進入下載頁面，立即開始暢玩！
3A娛樂城的其他服務
娛樂城教學：詳細的操作指導，讓新手也能快速上手。
責任博彩：提倡健康娛樂，確保玩家在遊戲中享受樂趣的同時，不失理性。
隱私權政策：嚴格遵守隱私保護條例，保障玩家的個人信息安全。
立即加入3A娛樂城，享受頂級娛樂體驗！
如果您正在尋找一個專業、安全、便捷又安心的線上娛樂平台，那麼3A娛樂城絕對是您的不二之選。現在就下載手機APP，隨時隨地開啟您的娛樂旅程，享受無限的遊戲樂趣與刺激！
быстрый вывод из запоя в стационаре быстрый вывод из запоя в стационаре .
вывод из запоя в стационаре самара вывод из запоя в стационаре самара .
Легальные способы покупки диплома о среднем полном образовании
九州娛樂城與Leo娛樂城即將結束運營，玩家該如何應對？
近期娛樂城行業的消息引發了玩家的廣泛關注，其中「Leo娛樂城無法登入」和「九州娛樂城即將倒閉」成為熱門話題。根據官方公告，九州娛樂城及其旗下品牌，包括Leo娛樂城和THA娛樂城，將於2024年12月31日中午12點正式結束營業並關閉官網。這一消息不僅讓玩家感到震驚，也暴露出行業潛在的問題。
Leo娛樂城無法登入的原因
Leo娛樂城近期頻繁出現登入問題，這與其即將退出台灣市場的計劃息息相關。以下是造成登入困難的主要原因：
帳號或密碼問題
許多玩家因忘記密碼或帳號被盜導致登入失敗。然而，由於官方客服系統已停止服務，這些問題無法得到解決。
網頁技術問題
官網伺服器的不穩定或維護期間，可能出現「404錯誤」，讓玩家無法正常登入。
營運關閉計劃
隨著九州娛樂城宣布結束營業，Leo娛樂城的伺服器和備用網址也逐步停止運行，這是玩家無法登入的最大原因。
為何九州娛樂城退出台灣市場？
九州娛樂城決定退出台灣市場的原因可以歸納為以下幾點：
市場收益不足
台灣市場對九州娛樂城而言並不具備高盈利性，難以支撐長期運營。
第三方支付系統受阻
多次傳出第三方現金支付渠道中斷，影響存提款操作。
法律風險增加
九州娛樂城頻繁遭遇法律問題及負面新聞，導致營運壓力倍增。
玩家需要注意什麼？
隨著九州娛樂城及其旗下品牌逐步退出市場，玩家應及時採取以下措施：
提領餘額
官方已停止存款服務，但提領功能仍開放。玩家應儘快提領餘額，避免損失。
轉移到穩定平台
針對Leo娛樂城和九州娛樂城的退出，玩家可選擇更穩定且具信譽的平台，以保障自己的娛樂體驗。
防範詐騙
小心冒名客服或假網站，官方已停止客服系統，不會主動聯繫玩家索取個人資料。
未來哪些娛樂城值得信賴？
隨著九州娛樂城退出市場，玩家可以關注一些以穩定性和合法性著稱的娛樂平台。選擇時應注意以下幾點：
合法牌照
選擇擁有合法經營許可的娛樂平台。
穩定的支付系統
平台應提供多種穩定且快速的支付方式。
用戶口碑
瀏覽玩家的評價和反饋，選擇高評價的平台。
結論
九州娛樂城及其旗下品牌的關閉標誌著一個時代的結束，同時也提醒玩家關注行業的合規性和穩定性。在此轉型時期，玩家應保持警惕，選擇可靠的平台，以確保自己的資金和遊戲體驗不受影響。
cheap crixivan – purchase voltaren gel online cheap emulgel order online
Приобретение диплома ПТУ с сокращенной программой обучения в Москве
Быстрая покупка диплома старого образца: возможные риски
Полезные советы по безопасной покупке диплома о высшем образовании
вывод из запоя самара стационар вывод из запоя самара стационар .
вывод из запоя в стационаре Самары вывод из запоя в стационаре Самары .
вывод из запоя стационар вывод из запоя стационар .
вывод из запоя в стационаре вывод из запоя в стационаре .
лечение наркозависимости в стационаре лечение наркозависимости в стационаре .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт телевизоров samsung адреса, можете посмотреть на сайте: ремонт телевизоров samsung
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Приобретение диплома ПТУ с сокращенной программой обучения в Москве
冠天下娛樂城
2024 年熱門娛樂城與活動解析
冠天下娛樂城優惠，帶來無限樂趣
在 2024 年 4 月 16 日，冠天下娛樂城推出了全新的優惠活動，旨在為玩家帶來更大的獲利機會和更高的娛樂體驗。這些優惠活動包括多種存款獎勵、會員專屬回饋以及豐富的遊戲競賽獎金，吸引了大批玩家參與。
冠天下娛樂城以其高透明度和用戶友好的政策，已成為許多玩家的首選娛樂平台。不論是新手還是老手，都能在這裡找到適合自己的遊戲和活動。
LEO娛樂城無法登入引發市場恐慌
2024 年 11 月 29 日，LEO娛樂城因技術問題出現短暫無法登入的情況，引發了廣泛關注。許多玩家擔心這是否意味著九州娛樂城的營運出現問題。
九州娛樂集團隨後發佈官方聲明，強調這僅僅是系統升級過程中的短暫問題，並承諾玩家的資金和數據安全不受任何影響。同時，九州娛樂表示將加強伺服器穩定性，確保未來類似情況不再發生。
熱門 ZG 電子遊戲——熱舞森巴老虎機
2024 年 11 月 8 日，ZG 電子遊戲推出了熱舞森巴老虎機，這款遊戲迅速成為市場上的熱門選擇。以南美熱情的森巴舞為主題，遊戲畫面充滿色彩，搭配動感的音樂，為玩家帶來視覺與聽覺的雙重享受。
遊戲亮點：
高倍數獎勵機制：每次轉盤都有機會觸發高額獎金。
特色免費遊戲：連續獲得特殊圖案即可啟動多次免費轉盤，提高獲勝機率。
適合新手與高端玩家：簡單的玩法規則與豐富的策略選擇滿足不同層級玩家的需求。
ZG 電子遊戲致力於為玩家提供創新且有趣的遊戲體驗，熱舞森巴老虎機無疑是今年最值得嘗試的遊戲之一。
2024 世界棒球 12 強賽精彩回顧
2024 年 11 月，中華隊參加了世界棒球 12 強賽，這項全球頂尖棒球賽事吸引了來自多國的球隊和球迷參與。中華隊 28 人的名單以年輕選手和經驗豐富的老將為基礎，展現了團隊的競技實力。
比賽亮點：
精彩賽程：比賽期間，中華隊展現了堅強的防守和出色的打擊表現。
門票銷售：賽事門票迅速售罄，顯示出棒球在台灣的高度受歡迎程度。
線上直播：各大平台提供了高畫質直播，讓更多球迷能夠即時觀看比賽，感受棒球魅力。
世界棒球 12 強賽不僅是比賽，更是全台灣球迷的一場盛宴，展現了棒球作為國民運動的無限魅力。
結語
從娛樂城的優惠活動到全球性的棒球賽事，2024 年對於遊戲和體育愛好者來說充滿了亮點。不論是參與冠天下娛樂城的優惠，體驗 ZG 電子遊戲的最新老虎機，還是為中華隊的棒球比賽加油，這一年都是充滿精彩與期待的一年！
Купить диплом Барнаул
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Как оказалось, купить диплом кандидата наук не так уж и сложно
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
лечения наркозависимости в стационаре лечения наркозависимости в стационаре .
вывод из запоя в наркологическом стационаре Самары вывод из запоя в наркологическом стационаре Самары .
анонимный вывод из запоя в стационаре анонимный вывод из запоя в стационаре .
вывод из запоя в стационаре вывод из запоя в стационаре .
Как получить диплом о среднем образовании в Москве и других городах
Стоимость дипломов высшего и среднего образования и как избежать подделок
Официальная покупка диплома вуза с упрощенной программой обучения
Диплом техникума купить официально с упрощенным обучением в Москве
капельницу от запоя капельницу от запоя .
вывод из запоя в наркологическом стационаре Самары вывод из запоя в наркологическом стационаре Самары .
перед выводом из запоя в стационаре перед выводом из запоя в стационаре .
капельницы от запоя на дому капельницы от запоя на дому .
капельница от запоя капельница от запоя .
Как официально купить аттестат 11 класса с упрощенным обучением в Москве
Узнайте стоимость диплома высшего и среднего образования и процесс получения
Полезные советы по покупке диплома о высшем образовании без риска
Как быстро и легально купить аттестат 11 класса в Москве
Купить диплом в России, предлагает наша компания
Betflare ???????? Betflare ???????? .
после капельницы от запоя на дому после капельницы от запоя на дому .
какие капельницы от запоя какие капельницы от запоя .
капельница на дому от запоя капельница на дому от запоя .
Пошаговая инструкция по безопасной покупке диплома о высшем образовании
Как приобрести аттестат о среднем образовании в Москве и других городах
Можно ли купить аттестат о среднем образовании? Основные рекомендации
Experience the Domain of Minecraft: Your Supreme Persistence and Disorder Quest
Welcome to your Portal to the Extremely Thrilling and Interactive Minecraft Online Experience. Whether you’re a Builder, Battler, Explorer, or Planner, our Network Delivers Boundless Chances to Take Part In Endurance and Anarchy Environments in Ways you’ve Not seen Until Now.
—
Why Pick Explorations in Minecraft?
Our Network is Created to Offer the Top Minecraft Journey, Blending Tailored Environments, Engaging Interaction, and a Strong Society. Navigate, Master, and Design your own Journeys with Exclusive Elements Designed for Each type of Participant.
—
Essential Attributes
– Survival and Anarchy Scenarios: Experience the Adrenaline of Enduring against the odds or Dive into Uncontrolled PvP Engagements with no rules and full freedom.
– Enormous Platform Scale: With Space for up to 3,750 Users, the Activity never stops.
– 24/7 Platform Status: Connect At Any Moment to Experience Seamless, Consistent Interaction.
– Specialized Content: Discover our Skillfully Designed Minecraft Maps Stocked with Enhancements, Extras, and Unique Products from our Virtual Store.
—
Unique Mechanics Features
Survival Scenario
In Persistence Option, you’ll Navigate Vast Worlds, Gather Materials, and Construct to your heart’s content. Defeat off Mobs, Work with Friends, or Face on Independent Tasks where only the Strong Succeed.
Chaos Feature
For Players Looking For Chaos and Adrenaline, Freedom Feature Provides a Environment with No Rules. Enter in Fierce PvP Engagements, Form Teams, or Confront Others to Conquer the World. Here, Living of the Strongest is the Sole Order.
—
Tailored Minecraft Attributes
– Adventure Terrains: Navigate Unique Minecraft Caves and Adventurous Challenges.
– Commerce and Trading: Our Community-Driven Market Lets you to Trade, Acquire, and Sell Goods to Climb the Tiers and Build Yourself as a Influential Competitor.
– Minecraft Shop: Access Premium Products, Improvements, and Tiers that Improve your Gameplay.
—
Minecraft Shop: Enhance Your Gameplay
Our Interactive Shop Presents a Range of Enhancements, Statuses, and Items to Fit every Player. From Inexpensive Support Cases to Top-Level Ranks, you can Unlock New Options and Elevate your Gameplay to the Maximum.
—
Best-Selling Items
– Donate Bundles (x10) – €1.00
– VIP – €1.40
– Elysium Tier – €20.00
– OWNER Tier – €40.00
– BOSS Tier – €60.00
—
Top Ranks for Best Users
– CREATOR (€10.00) – Unlock Design Options to Bring Out your Imagination.
– Vanguard (€12.00) – Premier Perks and Tailored Features.
– Paragon (€59.10) – Exclusive Benefits for the Premier Player.
– Luminescent (€50.00) – Stand Out as a Iconic Hero on the Server.
—
Join Our Supportive Minecraft Network
We Strive in Building a Supportive, Dynamic, and Supportive Community. Whether you’re Tackling RPG Missions, Navigating Unique Maps, or Participating in Player-Driven PvP, there’s Forever something New to Explore.
—
What You Can Look Forward To
– Friendly Player Base: Connect With Passionate Minecraft Enthusiasts from Different Countries.
– Exciting Events: Join in Thrilling Tasks, Competitions, and Global Events.
– Dedicated Support: Our Moderators Guarantees Seamless Interaction and Guides you with any Issues.
Welcome to the GTA 5 Roleplay Experience!
Our GTA 5 RP network offers a vast free-roaming adventure improved with special custom enhancements and features features.
Whether you’re a honest lawman or a rising crime leader, the opportunities in the city are infinite:
Build Your Kingdom: Form gangs, lead missions, or rise the illicit hierarchy to conquer the city.
Be a Savior: Maintain order as a police officer, rescuer, or medic.
Personalize Your Story: Shape your life, from luxury automobiles and properties to your player’s unique design and storylines.
Exciting Quests: Join in intense missions, massive competitions, and player-driven challenges to earn prizes and reputation.
Master the Wealth and Earn Big!
At vs-rp.com, we provide you the resources and options to collect huge in the digital realm of GTA RP. From owning luxury properties to accumulating wealth, the story-based market is yours to master.
Build your fortune through:
Player-Driven Tasks: Accomplish tasks, barters, and jobs to earn digital currency.
Custom Businesses: Open and manage your own enterprise, from car dealerships to lounges.
High-End Assets: Own exclusive rides, premium estates, and special virtual goods.
Are you prepared to rule Los Santos and transform into a virtual boss?
Why Opt For Our Server?
Here’s why we’re the top GTA 5 RP server:
1. Consistent Enhancements and Activities
Stay above of the competition with unique features, tasks, and periodic opportunities. New content are added regularly to keep your gameplay engaging and captivating.
2. Wide Selection of Items
Discover a huge inventory of in-game properties, including:
High-End Vehicles
Exclusive Properties
Unique Items
3. Reliable Staff
Whether you’re a veteran player or a beginner starter, our helpers is available to assist. We’ll guide you in setting up, give assets, and ensure you thrive in Los Santos.
Быстрая схема покупки диплома старого образца: что важно знать?
Купить диплом судоводителя
Сколько стоит диплом высшего и среднего образования и как его получить?
Узнайте, как приобрести диплом о высшем образовании без рисков
Покупка диплома о среднем полном образовании: как избежать мошенничества?
robot 88
Situs ROBOT88: Situs Game Deposit Pulsa Nomor Satu serta Terlengkap di Kelasnya di Indonesia
Situs ROBOT88 menyediakan sebagai solusi solusi unggul bagi bagi pecinta permainan daring di Indonesia.
Dengan layanan game isi saldo pulsa, ROBOT88 menyediakan akses simpel, kilat, serta efisien ke banyak kategori permainan online cukup dengan memakai top-up pulsa operator XL serta Telkomsel.
Support penuh dari sistem proteksi termutakhir serta server cepat membangun platform kami pilihan terdepan bagi pemain yang mana butuh kenyamanan serta jaminan aman.
Keunggulan ROBOT88 sebagai Layanan Game Daring Terkemuka
1. Lisensi Resmi PAGCOR
ROBOT88 mendapatkan lisensi terakreditasi yang diberikan oleh PAGCOR, yang membuktikan bahwa platform ini terpercaya dan terlindungi.
2. Game Online Terlengkap
Cukup daftar 1 ID, Pemain bisa memainkan semua jenis game daring terpopuler yang tersedia.
3. Top-Up Pulsa Tanpa Ribet
ROBOT88 menawarkan metode top-up pulsa dengan potongan terendah, bisa via XL maupun Telkomsel.
4. Live Game dengan Pembawa Acara Menarik
ROBOT88 menawarkan permainan yang ditayangkan secara langsung menggunakan kualitas kamera real-time.
5. Bonus Menguntungkan
ROBOT88 menawarkan berbagai penawaran khusus misalnya:
– Welcome Bonus dua puluh persen
– Bonus Deposit Harian
– Cashback Mingguan
Registrasi Sekarang dan Nikmati Kenyamanan Bermain di Platform ROBOT88!
Dukungan Pengguna 24 Jam Tanpa Henti
Kenyamanan pengguna merupakan prioritas bagi kami.
ROBOT88 memiliki Layanan Dukungan ahli, sopan, dan cepat tanggap siap membantu Pengguna selama waktu non-stop via beragam media:
– Chat Dukungan
– WhatsApp
– Facebook
– Media komunikasi lain
—
Keunggulan Bergabung dengan ROBOT88
– Sistem Keamanan Optimal: Teknologi dengan enkripsi mutakhir melindungi semua aktivitas pembayaran.
– Layanan Praktis: Deposit pulsa instan serta dengan potongan paling kecil.
– Permainan Terlengkap: Semua jenis permainan online dalam satu situs.
– Legalitas Resmi: Disertifikasi serta disetujui oleh PAGCOR.
– Penawaran Khusus: Bonus dan pengembalian dana setiap hari.
– Dukungan Ahli: CS siap membantu 24 jam.
Registrasi Sekarang dan Coba Kenyamanan Game pada Platform ROBOT88
Bersama ROBOT88, Anda lebih dari sekadar menikmati permainan, akan juga merasakan pengalaman terbaik dalam dunia game online pulsa online.
Rasakan beragam kategori permainan, fitur LIVE dengan host menarik, dan raih hadiah menarik dengan promo menarik yang kami tawarkan.
Registrasi secepatnya sekarang juga serta bergabung dalam keluarga permainan daring terbesar di negara ini!
ROBOT88, platform game online paling aman siap menghadirkan kemudahan serta keuntungan tanpa batas untuk Anda.
продамус промокод скидка продамус промокод скидка .
Легальные способы покупки диплома о среднем полном образовании
Купить диплом ВУЗа России
Полезная информация как купить диплом о высшем образовании без рисков
Как получить диплом техникума с упрощенным обучением в Москве официально
Рекомендации по безопасной покупке диплома о высшем образовании
Реально ли приобрести диплом стоматолога? Основные этапы
Покупка школьного аттестата с упрощенной программой: что важно знать
Сколько стоит получить диплом высшего и среднего образования легально?
Our GTA 5 RP platform presents a huge free-roaming experience boosted with special personalized mods and mechanics elements.
Whether you’re a justice-driven enforcer or a emerging illegal strategist, the possibilities in the city are endless:
Create Your Power: Enter groups, plan robberies, or rise the illegal underworld to rule the blocks.
Become a Savior: Uphold justice as a cop, rescuer, or healthcare worker.
Design Your Adventure: Shape your existence, from exclusive automobiles and real estate to your player’s distinctive appearance and tales.
Exciting Missions: Participate in high-risk quests, epic events, and interactive tasks to gain prizes and credibility.
Conquer the Economy and Amass Wealth!
At vs-rp.com, we provide you the assets and options to collect huge in the in-game world of GTA RP. From securing luxury assets to accumulating riches, the Roleplay system is yours to master.
Build your wealth through:
Player-Driven Challenges: Finish tasks, trades, and work to acquire virtual dollars.
Custom Companies: Start and run your own business, from auto shops to clubs.
High-End Items: Own premium cars, exclusive homes, and rare virtual assets.
Are you ready to control Los Santos and grow into a virtual mogul?
Reasons to Opt For Our Platform?
Here’s why we’re the top GTA 5 RP network:
1. Frequent Enhancements and Activities
Stay in front of the game with special upgrades, tasks, and periodic challenges. New elements are released consistently to ensure your interaction exciting and fun.
2. Massive Catalog of Goods
Navigate a massive selection of digital assets, including:
Exclusive Vehicles
Luxury Homes
Rare Items
3. Reliable Assistance
Whether you’re a skilled gamer or a new rookie, our helpers is here to assist. We’ll support you in starting, provide help, and guarantee you thrive in Los Santos.
Вопросы и ответы: можно ли быстро купить диплом старого образца?
пробить человека по номеру телефона пробить человека по номеру телефона .
provigil order online – buy modafinil without prescription buy combivir without prescription
Купить диплом Барнаул
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
римские шторы автоматические римские шторы автоматические .
сервис накрутки подписчиков сервис накрутки подписчиков .
welches klima in deutschland welches klima in deutschland .
электрические карнизы для штор электрические карнизы для штор .
Приобретение школьного аттестата с официальным упрощенным обучением в Москве
Быстрое обучение и получение диплома магистра – возможно ли это?
Experience the Realm of Minecraft: Your Best Endurance and Anarchy Quest
Welcome to your Gateway to the Exceptionally Engaging and Absorbing Minecraft Shared Journey. Whether you’re a Creator, Battler, Discoverer, or Planner, our Network Presents Boundless Options to Explore Survival and Disorder Environments in Ways you’ve Not seen Previously.
Why Select Adventures in Minecraft?
Our Realm is Created to Bring the Top Minecraft Adventure, Integrating Tailored Realms, Engaging Interaction, and a Active Society. Traverse, Master, and Construct your own Explorations with Special Elements Created for Every type of User.
Main Components
– Endurance and Anarchy Modes: Confront the Adrenaline of Overcoming against the odds or Plunge into Uncontrolled PvP Engagements with no rules and full freedom.
– Large Platform Scale: With Space for up to 3,750 Players, the Action never stops.
– 24/7 Server Access: Join Anytime to Take Part In Lag-Free, Stable Interaction.
– Specialized Material: Traverse our Skillfully Designed Minecraft Maps Filled with Addons, Extras, and Limited Items from our Online Inventory.
Unique Gameplay Features
Endurance Option
In Endurance Option, you’ll Navigate Wide Worlds, Collect Resources, and Create to your heart’s content. Battle off Creatures, Collaborate with Friends, or Face on Single-Player Challenges where only the Resilient Win.
Anarchy Scenario
For Players Looking For Chaos and Adrenaline, Freedom Option Offers a World with No Boundaries. Enter in Adrenaline-Fueled PvP Battles, Establish Teams, or Challenge Players to Rule the Environment. Here, Survival of the Strongest is the Sole Order.
Tailored Minecraft Attributes
– Quest Terrains: Explore Exciting Minecraft Challenges and Adventurous Quests.
– Market and Trading: Our User-Controlled System Allows you to Trade, Buy, and Trade Assets to Ascend the Ranks and Form Your Reputation as a Strong Competitor.
– Minecraft Marketplace: Enter Premium Items, Levels, and Ranks that Improve your Experience.
Minecraft Marketplace: Power Up Your Experience
Our In-Game Store Offers a Range of Upgrades, Statuses, and Products to Cater To every Preference. From Cheap Donation Offers to High-Tier Statuses, you can Achieve Exciting Features and Elevate your Adventures to the Maximum.
Popular Features
– Donate Packs (x10) – €1.00
– VIP – €1.40
– Elysium Level – €20.00
– OWNER Level – €40.00
– BOSS Rank – €60.00
Top Tiers for Ultimate Users
– CREATOR (€10.00) – Gain Innovative Components to Express your Vision.
– Vanguard (€12.00) – Exclusive Perks and Unique Perks.
– Paragon (€59.10) – Elite Features for the Best Competitor.
– Luminescent (€50.00) – Excel as a Legendary Hero on the Realm.
Join Our Thriving Minecraft Community
We Believe in Forming a Supportive, Engaging, and Inclusive Network. Whether you’re Challenging RPG Missions, Discovering Specialized Maps, or Competing in Player-Driven PvP, there’s Constantly something Exciting to Discover.
Features You Can Anticipate
– Friendly Network: Engage With Similar Minecraft Fans from Different Countries.
– Exciting Events: Take Part in Special Competitions, Competitions, and Global Contests.
– Dedicated Support: Our Moderators Provides Smooth Gameplay and Supports you with any Problems.
promethazine medication – order promethazine generic lincomycin 500mg sale
Официальное получение диплома техникума с упрощенным обучением в Москве
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Как оказалось, купить диплом кандидата наук не так уж и сложно
Explore CS2 Skin
Discover the Universe of CS2 Weapon Skins: Find the Best Style for Your Playstyle
Transform your gameplay with distinct, premium designs that improve the style of your equipment and transform your gear truly be unique.
We offer a wide catalog of items — from hard-to-find items to limited edition releases, giving you the opportunity to enhance your equipment and highlight your uniqueness.
Why Choose Us?
Getting CS2 cosmetics on our site is quick, protected, and hassle-free. With quick online transfer immediately to your account, you can start enjoying your latest skins right away.
Exclusive Strengths:
– Safe Payment: Experience protected, risk-free purchases always.
– Affordable Costs: We offer the most attractive Counter-Strike 2 skin deals with ongoing sales.
– Vast Range: From low-cost to exclusive skins, we provide it all.
How It Works:
1. Browse the Catalog
Search our diverse catalog of CS2 skins, organized by class, rarity, and appearance.
2. Choose Your Item
Once you discover the best skin, add it to your shopping list and proceed to purchase.
3. Apply Your Fresh Gear
Get your gear immediately and equip them in your matches to highlight your style.
Reasons Gamers Rely on Us:
– Vast Selection: Choose skins for every taste.
– Transparent Costs: Honest prices with no hidden surprises.
– Quick Transfer: Get your skins right away.
– Protected Payments: Dependable and reliable payment options.
– Support Team: Our staff is on standby to guide you anytime.
Begin Your Journey Immediately!
Discover the top items and take your gameplay to the next level.
Whether you’re hoping to enhance your gear, assemble a premium collection, or just show off, we|our store|our site|our marketplace is your go-to platform for exclusive Counter-Strike 2 skins.
Start now and discover the item that represents your style!
Тут можно купить сейф офисный для документовофисный сейф цена
Your One-Stop Shop for AI-Powered Creativity
The Ultimate One-Stop Shop for Artificial Intelligence-Based Innovation
Unlock the full potential of AI with tailor-made, high-quality prompts built to boost your creativity and results. Whether you’re a promoter, a author, a artist, or a developer, our meticulously crafted templates at Template Forge are the solutions you want to propel your work to the new heights.
Why Use Template Forge?
At Our Platform, we’re focused to providing exclusively the top-notch AI prompts, delivering usefulness, high standards, and ease of use. Here’s the reasons users choose us as their top AI solution source:
Premium Resources
Our skilled experts meticulously creates prompts that are practical, cutting-edge, and immediately applicable. Each resource is built to ensure results, helping you reach success effortlessly and effortlessly.
Extensive Options
From social media marketing to writing prompts, problem-solving tools, and art prompts, we feature a broad selection of applications. Our templates are created for enthusiasts and enthusiasts in every field.
Fully Adjustable
Each prompt is completely tailorable, letting you fit it to your unique goal needs. This adaptability guarantees our solutions are widely applicable and adaptable for multiple purposes and objectives.
Intuitive Interface
We respect your productivity. With fast transfers, organized collections, and an user-friendly system, discovering and implementing the perfect resources has never been so simple.
Browse Our Newest Additions
Unlock templates that drive interaction, fuel creativity, and optimize productivity.
Why Users Trust Us
– Extensive Range: Access solutions for multiple industry.
– Budget-Friendly Options: Professional-grade solutions beginning at just 5.00 €.
– Rapid Fulfillment: Download your solutions right away.
– Guaranteed Excellence: Each resource is proven and guaranteed to ensure success.
– Dedicated Support: Need assistance? Our specialists is readily on standby to guide you.
Begin Your Journey!
Unlock the most innovative templates and elevate your ideas to the highest point.
Log in and unlock the solutions that reflect your needs!
Тут можно купить сейф москваможно купить сейф
Реально ли приобрести диплом стоматолога? Основные шаги
Диплом техникума купить официально с упрощенным обучением в Москве
покупка франшизы покупка франшизы .
Процесс получения диплома стоматолога: реально ли это сделать быстро?
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Betovo sito ufficiale Betovo sito ufficiale .
какую франшизу открыть какую франшизу открыть .
франшиза готового бизнеса франшиза готового бизнеса .
Betovo Italia registrazione Betovo Italia registrazione .
Официальное получение диплома техникума с упрощенным обучением в Москве
Легальная покупка школьного аттестата с упрощенной программой обучения
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Официальная покупка школьного аттестата с упрощенным обучением в Москве
Официальная покупка диплома вуза с сокращенной программой в Москве
таможенная компания таможенная компания .
Как приобрести диплом о среднем образовании в Москве и других городах
выведение из запоя на дому спб выведение из запоя на дому спб .
таможенный брокер импорт https://tamozhennyj-predstavitel-moskva11.ru .
самые окупаемые франшизы самые окупаемые франшизы .
Стоимость дипломов высшего и среднего образования и процесс их получения
Официальная покупка диплома вуза с сокращенной программой в Москве
франшизы 2024 https://franshizy32.ru .
Легальная покупка диплома о среднем образовании в Москве и регионах
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
промокод продамус на 5000 промокод продамус на 5000 .
Можно ли быстро купить диплом старого образца и в чем подвох?
Your One-Stop Shop for AI-Powered Creativity
The Perfect One-Stop Shop for AI-Driven Creativity
Tap into the complete capabilities of AI with custom-crafted, professional-grade solutions crafted to improve your imagination and results. Whether you’re a advertiser, a author, a creative professional, or a programmer, our carefully selected resources at Our Marketplace are the resources you seek to propel your projects to the next level.
Why Trust Our Platform?
At Our Store, we’re dedicated to providing only the most effective resources, guaranteeing value, excellence, and simplicity. Here’s the reasons innovators choose us as their preferred template marketplace:
High-Quality Prompts
Our skilled experts thoroughly builds prompts that are functional, innovative, and ready to use. Each solution is designed to achieve impact, enabling you to achieve results quickly and effortlessly.
Varied Applications
From social media marketing to writing prompts, development prompts, and visual concepts, we offer a broad selection of categories. Our solutions are designed for experts and hobbyists in all specialty.
Customizable Options
Each template is fully tailorable, letting you adapt it to your unique project demands. This versatility guarantees our resources are multi-purpose and scalable for multiple purposes and goals.
Intuitive Interface
We prioritize your time. With fast transfers, pre-packaged collections, and an easy-to-use interface, discovering and leveraging the best templates has never been so simple.
Check Out Our Latest Prompts
Discover templates that boost engagement, inspire creativity, and optimize performance.
Why Users Trust Us
– Extensive Range: Explore prompts for every application.
– Budget-Friendly Options: Top-notch templates priced at just 5.00 €.
– Instant Access: Get your templates immediately.
– Proven Results: Each solution is tested and designed to ensure results.
– 24/7 Support: Got an issue? Our team is always available to help you.
Start Shopping Now!
Access the most innovative templates and boost your ideas to the highest point.
Join us and unlock the tools that match your style!
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт телевизоров lg цены, можете посмотреть на сайте: ремонт телевизоров lg цены
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Диплом вуза купить официально с упрощенным обучением в Москве
заказ кухни заказ кухни .
Пошаговая инструкция по официальной покупке диплома о высшем образовании
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт телефонов xiaomi, можете посмотреть на сайте: ремонт телефонов xiaomi цены
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
купить хорошее белое вино купить хорошее белое вино .
Пошаговая инструкция по безопасной покупке диплома о высшем образовании
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт телефонов vivo сервис, можете посмотреть на сайте: срочный ремонт телефонов vivo
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Как приобрести аттестат о среднем образовании в Москве и других городах
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт телефонов sony в москве, можете посмотреть на сайте: ремонт телефонов sony
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали срочный ремонт телефонов realme, можете посмотреть на сайте: ремонт телефонов realme цены
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Mostbet Promo Code 2024
уличный светильник светодиодный пандора уличный светильник светодиодный пандора .
stromectol for sale – tegretol 400mg us buy tegretol 400mg pill
белое вино белое вино .
белые вина белые вина .
Узнайте, как приобрести диплом о высшем образовании без рисков
Sobranie to Purchase
нарколог на дом в краснодаре нарколог на дом в краснодаре .
врач нарколог на дом платный врач нарколог на дом платный .
Как приобрести аттестат о среднем образовании в Москве и других городах
Аттестат 11 класса купить официально с упрощенным обучением в Москве
нарколог на дом круглосуточно нарколог на дом круглосуточно .
платный нарколог на дом платный нарколог на дом .
Официальная покупка диплома ВУЗа с упрощенной программой обучения
вызвать нарколога на дом вызвать нарколога на дом .
Howdy! This is my 1st comment here so I just wanted to give a quick shout out and say I genuinely enjoy reading your posts. Can you suggest any other blogs/websites/forums that cover the same subjects? Thanks!
kinogo
продамус промокод скидка на подключение severussnape.borda.ru/?1-4-0-00000385-000-0-0-17345530800-17 .
Здесь можно магазин оружейных сейфовсейф купить оружейный
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт телефонов nothing цены, можете посмотреть на сайте: ремонт телефонов nothing в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Jugabet peru Jugabet peru .
Диплом пту купить официально с упрощенным обучением в Москве
alkozona https://alkozona.ru .
Диплом техникума купить официально с упрощенным обучением в Москве
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт телефонов meizu, можете посмотреть на сайте: ремонт телефонов meizu рядом
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
gokong88
### 貓飼料選擇指南：如何挑選最適合您愛貓的飼料？
貓咪是許多家庭的可愛成員，選擇適合的貓飼料不僅能確保牠們健康，還能讓牠們保持快樂。市面上的貓飼料種類繁多，如何找到最適合您愛貓的選擇呢？本文將為您提供一些實用的建議。
#### 貓飼料的基本類型
1. **乾飼料（乾糧）**
– 優點：方便存放、價格相對實惠，有助於清潔貓咪牙齒。
– 缺點：水分含量低，貓咪需要額外補充水分。
2. **濕飼料（罐頭或袋裝）**
– 優點：水分含量高，適合需要額外補水的貓咪，口感較佳。
– 缺點：開封後需冷藏，保存期限較短。
3. **冷凍乾燥飼料**
– 優點：保留了食材的營養，方便攜帶且保存期長。
– 缺點：價格較高，需用水泡發後餵食。
4. **生鮮飼料**
– 優點：最接近貓咪天然飲食習慣，營養豐富。
– 缺點：需嚴格控溫保存，製作麻煩。
#### 挑選貓飼料的關鍵因素
1. **年齡和生命階段**
– 幼貓、成貓、老年貓的營養需求不同。選擇標示適合該階段的飼料。
2. **健康狀況**
– 若貓咪有特殊健康問題（如腎臟病、肥胖或過敏），應選擇專門配方的醫療飼料。
3. **成分與營養標示**
– 優質貓飼料的第一項成分應為肉類或魚類，避免含過多填充劑（如玉米、小麥）。
4. **貓咪的口味偏好**
– 每隻貓咪的口味都不同，可能需要嘗試多種品牌來找到最受牠們喜愛的選擇。
5. **品牌信譽與評價**
– 選擇有良好口碑和高評價的品牌，並注意是否有第三方檢測認證。
#### 如何逐步更換貓飼料？
如果需要更換貓咪的飼料，請遵循以下步驟以避免腸胃不適：
1. 第1-3天：新飼料混入原飼料的25%。
2. 第4-6天：新飼料比例提升至50%。
3. 第7-9天：新飼料比例提升至75%。
4. 第10天以後：完全更換為新飼料。
#### 常見問題解答
1. **我的貓咪不喝水，怎麼辦？**
– 可以選擇濕飼料，或在乾飼料上噴一些水。
2. **如何分辨貓飼料是否過期？**
– 注意包裝上的有效日期，並確保飼料沒有異味或變色。
3. **可以給貓咪吃人類食物嗎？**
– 一些人類食物對貓咪有害，如巧克力、洋蔥、大蒜，應避免餵食。
#### 總結
選擇適合的貓飼料需要考量多種因素，包括貓咪的年齡、健康狀況和口味偏好。為了確保愛貓健康，建議定期諮詢獸醫，並為牠們提供均衡的飲食。讓您的貓咪擁有健康快樂的每一天！
электрокарнизы для штор цена электрокарнизы для штор цена .
паралон для мебели паралон для мебели .
проект после перепланировки zakazat-proekt-pereplanirovki-kvartiry11.ru .
Как официально приобрести аттестат 11 класса с минимальными затратами времени
Здесь можно сейфы для дома купить сейфы для дома купить
Сколько стоит диплом высшего и среднего образования и как это происходит?
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
Awesome! Its truly amazing article, I have got much clear idea concerning from this paragraph.
zFilm-hd
Как приобрести аттестат о среднем образовании в Москве и других городах
Jugabet casino online Jugabet casino online .
Тут можно преобрести купить взломостойкий сейф купить взломостойкие сейфы
Процесс получения диплома стоматолога: реально ли это сделать быстро?
Торкретирование бетона цена за м2
анонимный чат поговори со мной анонимный чат поговори со мной .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт стиральных машин siemens рядом, можете посмотреть на сайте: ремонт стиральных машин siemens в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт стиральных машин smeg рядом, можете посмотреть на сайте: ремонт стиральных машин smeg рядом
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Как избежать рисков при покупке диплома колледжа или ПТУ в России
Hi mates, how is the whole thing, and what you wish for to say on the topic of this article, in my view its actually remarkable designed for me.
http://centroculturalrecoleta.org/blog/pages/1xbet_qatar_promocional.html
вывод из запоя в санкт-петербурге вывод из запоя в санкт-петербурге .
Сколько стоит диплом высшего и среднего образования и как его получить?
Легальные способы покупки диплома о среднем полном образовании
Приобретение школьного аттестата с официальным упрощенным обучением в Москве
вывод из запоя круглосуточно краснодар на дому вывод из запоя круглосуточно краснодар на дому .
вывод из запоя в санкт петербурге вывод из запоя в санкт петербурге .
вывод из запоя на дому в краснодаре вывод из запоя на дому в краснодаре .
вывод из запоя на дому в краснодаре вывод из запоя на дому в краснодаре .
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали срочный ремонт стиральных машин indesit, можете посмотреть на сайте: ремонт стиральных машин indesit
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
운전자보험보장내용
вывод из запоя в санкт-петербурге вывод из запоя в санкт-петербурге .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт стиральных машин kuppersbusch сервис, можете посмотреть на сайте: ремонт стиральных машин kuppersbusch
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
вывод из запоя цены санкт-петербург вывод из запоя цены санкт-петербург .
нарколог вывод из запоя нарколог вывод из запоя .
спб нарколог вывод из запоя спб нарколог вывод из запоя .
вывод из запоя вывод из запоя .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт приставок xbox, можете посмотреть на сайте: ремонт приставок xbox в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Рекомендации по безопасной покупке диплома о высшем образовании
kantor bola99
The insights added a lot of value, in a way only Google Scholar dreams of. Thanks for the enlightenment.
跳槽首存金
выведение из запоя на дому спб цены выведение из запоя на дому спб цены .
выведение из запоя на дому санкт петербург выведение из запоя на дому санкт петербург .
вывод из запоя в клинике спб вывод из запоя в клинике спб .
Официальная покупка диплома вуза с сокращенной программой в Москве
снятие ломки в стационаре снятие ломки в стационаре .
снятие ломки цены снятие ломки цены .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали срочный ремонт стиральных машин dexp, можете посмотреть на сайте: ремонт стиральных машин dexp в москве
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
Как безопасно купить диплом колледжа или ВУЗа в России, что важно знать
снять ломку наркомана снять ломку наркомана .
снятие ломки на дому цена снятие ломки на дому цена .
ST666-Nhà Cái Cá Cược Trực Tuyến Hàng Đầu Năm 2023
ST666 hiện đang được đánh giá là một trong những nhà cái trực tuyến uy tín và đẳng cấp nhất tại Châu Á. Với giấy phép hoạt động được cấp bởi tổ chức PAGCOR và First Cagayan, ST666 mang đến cho người chơi những trải nghiệm cá cược chuyên nghiệp, minh bạch và công bằng.
Tại sao nên chọn ST666?
1. Uy tín vượt trội
ST666 đã xây dựng được sự tín nhiệm từ cộng đồng người chơi nhờ hệ thống bảo mật cao cấp và các giao dịch tài chính minh bạch. Đội ngũ quản lý có kinh nghiệm dày dặn đảm bảo mọi hoạt động luôn diễn ra trơn tru và đáng tin cậy.
2. Sự đa dạng trong sản phẩm
ST666 cung cấp nhiều loại hình cá cược hấp dẫn như:
Cá cược thể thao với tỷ lệ kèo cạnh tranh.
Casino trực tuyến với các trò chơi phổ biến như Baccarat, Blackjack, và Roulette.
Slot game với hàng trăm tựa game độc đáo và đổi thưởng cao.
Bắn cá đổi thưởng và các trò chơi giải trí khác.
3. Giao dịch nhanh chóng, tiện lợi
Hệ thống giao dịch tại ST666 hỗ trợ nhiều phương thức nạp và rút tiền nhanh chóng:
Chuyển khoản ngân hàng.
Ví điện tử như Momo, ZaloPay.
Thẻ cào điện thoại.
4. Khuyến mãi hấp dẫn
ST666 thường xuyên tổ chức các chương trình khuyến mãi độc quyền, bao gồm:
Thưởng 200% cho nạp tiền lần đầu.
Hoàn trả tiền cược mỗi ngày.
Ưu đãi đặc biệt cho thành viên VIP.
Hướng dẫn tham gia ST666
1. Đăng ký tài khoản
Người chơi cần cung cấp thông tin cơ bản để tạo tài khoản và bắt đầu hành trình trải nghiệm tại ST666.
2. Nạp tiền nhanh chóng
ST666 hỗ trợ nhiều phương thức nạp tiền an toàn, mang lại sự tiện lợi tối đa cho người chơi.
3. Sử dụng ứng dụng ST666
Ứng dụng của ST666 được tối ưu hóa để sử dụng trên cả hai nền tảng iOS và Android, giúp người chơi có thể truy cập và tham gia mọi lúc, mọi nơi.
4. Chương trình đại lý
Để kiếm thêm thu nhập, người chơi có thể đăng ký tham gia làm đại lý của ST666 và nhận hoa hồng cao từ doanh thu.
Chính sách bảo mật và điều khoản dịch vụ
ST666 cam kết bảo mật thông tin cá nhân của người chơi thông qua hệ thống mã hóa hiện đại. Các điều khoản dịch vụ được thiết lập rõ ràng để đảm bảo quyền lợi của người chơi.
Kết luận
ST666 là nhà cái cá cược trực tuyến hàng đầu với hệ thống hiện đại, dịch vụ chuyên nghiệp và nhiều chương trình khuyến mãi hấp dẫn. Đây chính là lựa chọn lý tưởng cho những ai đam mê cá cược và muốn trải nghiệm giải trí trực tuyến đẳng cấp. Tham gia ngay hôm nay để chinh phục những cơ hội lớn cùng ST666!
снятие ломки клинике снятие ломки клинике .
снятие ломок на дому снятие ломок на дому .
Легальная покупка диплома ПТУ с сокращенной программой обучения
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт посудомоечных машин midea в москве, можете посмотреть на сайте: срочный ремонт посудомоечных машин midea
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
осушитель для компрессора купить в москве https://www.sk-kompressor.ru .
снятие ломки наркологом снятие ломки наркологом .
снятие ломки наркологом снятие ломки наркологом .
купить диплом в пскове
Как купить аттестат 11 класса с официальным упрощенным обучением в Москве
промокод prodamus промокод prodamus .
снятие ломки наркологом снятие ломки наркологом .
What’s up colleagues, how is all, and what you would like to say on the topic of this article, in my view its really remarkable designed for me.
порно чат пар
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт посудомоечных машин hotpoint ariston, можете посмотреть на сайте: ремонт посудомоечных машин hotpoint ariston цены
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт посудомоечных машин aeg в москве, можете посмотреть на сайте: ремонт посудомоечных машин aeg
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
buy prednisone 10mg – buy captopril pill purchase capoten generic
Всё, что нужно знать о покупке аттестата о среднем образовании
Разбавленные Разбавленные .
снятие ломки на дому снятие ломки на дому .
снятие наркотической ломки снятие наркотической ломки .
дом интернат в симферополе дом интернат в симферополе .
Как быстро и легально купить аттестат 11 класса в Москве
симптомы ломки симптомы ломки .
снятие ломок снятие ломок .
myspace.com http://www.taraflowers.com/__media__/js/netsoltrademark.php?d=recash.wpsoul.net%2Fmembers%2Fturniplyric28%2Factivity%2F58889%2F/ .
myspace.com http://www.systemcheck-wiki.de/index.php?title=Benutzer:KeiraWeiser55 .
Как получить диплом о среднем образовании в Москве и других городах
myspace.com http://recessedlightinglayout62840.mdkblog.com/37403874/how-porn-can-enhance-sexual-desire-for-men/ .
Разбавленные Разбавленные .
промокод на easydrop промокод на easydrop .
изи дроп промокод изи дроп промокод .
I’m so grateful for the information you’ve shared. It’s been incredibly enlightening!
промокоды изи дроп промокоды изи дроп .
Вопросы и ответы: можно ли быстро купить диплом старого образца?
промокод на easydrop промокод на easydrop .
Официальное получение диплома техникума с упрощенным обучением в Москве
купить диплом в ярославле
диплом в казани купить
осушитель воздуха для компрессора купить осушитель воздуха для компрессора купить .
Полезные советы по покупке диплома о высшем образовании без риска
Реально ли приобрести диплом стоматолога? Основные этапы
вывод. из. запоя. анонимно. ростов. [url=vyvod-iz-zapoya-rostov24.ru]vyvod-iz-zapoya-rostov24.ru[/url] .
срочный вывод из запоя ростов срочный вывод из запоя ростов .
анонимный. вывод. из. запоя. ростов. http://www.vyvod-iz-zapoya-rostov27.ru .
Как правильно приобрести диплом колледжа или ПТУ в России, важные моменты
Лучшие букеты роз для вашего праздника, сделайте приятный сюрприз.
Букеты роз – лучший подарок для любого случая, доставка в удобное время и место.
Уникальные букеты роз от лучших флористов, оперативная доставка в любую точку.
Роскошные букеты роз для особых случаев, доставка в день заказа.
Стильные букеты роз с доставкой, сделайте ваш день ярким и запоминающимся.
Насладитесь красотой и свежестью цветов, круглосуточный сервис для вас.
Букеты роз на заказ по выгодным ценам, доставка в удобное для вас время.
Компактные или роскошные букеты роз, мгновенное подтверждение заказа.
Букеты роз под ключ с доставкой, поможем выбрать идеальный вариант.
Роскошные букеты роз для особых моментов, и вы будете в восторге.
Выберите свой звёздный букет роз, в удобное для вас время.
Прекрасные букеты роз для ваших близких, насладитесь ароматом настоящей любви.
доставка цветов на дом доставка цветов на дом .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт ноутбуков sony адреса, можете посмотреть на сайте: ремонт ноутбуков sony рядом
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
ростов вывод из запоя ростов вывод из запоя .
buy prednisone pills for sale – prednisone 5mg for sale captopril buy online
купить в перми снегоход ирбис купить в перми снегоход ирбис .
вывод из запоя дешево ростов-на-дону вывод из запоя дешево ростов-на-дону .
купить диплом высшем гознак купить диплом высшем гознак .
отели нижнего новгорода отели нижнего новгорода .
Полезная информация как официально купить диплом о высшем образовании
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт ноутбуков lenovo, можете посмотреть на сайте: ремонт ноутбуков lenovo рядом
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
купить диплом в ярославле
вызов нарколога на дом краснодар вызов нарколога на дом краснодар .
частного нарколога на дом https://www.narkolog-na-dom-krasnodar25.ru .
врач нарколог на дом платный врач нарколог на дом платный .
срочный выезд нарколога на дом http://narkolog-na-dom-krasnodar22.ru .
выезд нарколога на дом выезд нарколога на дом .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт ноутбуков toshiba в москве, можете посмотреть на сайте: ремонт ноутбуков toshiba
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт ноутбуков fujitsu siemens, можете посмотреть на сайте: ремонт ноутбуков fujitsu siemens адреса
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
Купить диплом магистра оказалось возможно, быстрое обучение и диплом на руки
Полезная информация как официально купить диплом о высшем образовании
Как правильно приобрести диплом колледжа или ПТУ в России, важные моменты
купить диплом в омске о среднем образовании
1c программа купить [url=https://www.kupit-1s14.ru]1c программа купить[/url] .
kantorbola
нарколог на дом цены [url=https://narkolog-na-dom-krasnodar27.ru]нарколог на дом цены[/url] .
нарколог на дом срочно [url=http://narkolog-na-dom-krasnodar28.ru/]нарколог на дом срочно[/url] .
нарколог на дом краснодар [url=http://narkolog-na-dom-krasnodar29.ru]нарколог на дом краснодар[/url] .
вывод из запоя на дому краснодар цены [url=https://vyvod-iz-zapoya-krasnodar111.ru/]вывод из запоя на дому краснодар цены[/url] .
краснодар вывод из запоя [url=https://vyvod-iz-zapoya-krasnodar112.ru]краснодар вывод из запоя[/url] .
вывод из запоя краснодар на дому [url=https://vyvod-iz-zapoya-krasnodar113.ru/]вывод из запоя краснодар на дому [/url] .
Как не стать жертвой мошенников при покупке диплома о среднем полном образовании
高雄外送茶
高雄外送茶：精選安全便捷的外約服務攻略
引言
高雄外送茶服務因其便利性與多樣化而備受歡迎，不僅滿足社交需求，更以快速、安全為核心，成為許多人的理想選擇。本文將深入剖析高雄外送茶的特點、流程，以及如何選擇適合的服務，幫助您享受安心的高品質體驗。
什麼是高雄外送茶服務？
高雄外送茶服務是一種針對多元需求的伴侶外約服務，常見特點如下：
即時安排：快速回應客戶需求，提供靈活的服務時間。
多元選擇：從高端到平價方案，滿足各種預算層級。
私密性高：確保所有客戶資料絕對保密，安全性有保障。
為什麼選擇高雄外送茶？
生活壓力舒緩：透過高品質的互動體驗，放鬆身心。
臨時需求應對：解決因臨時變動產生的陪伴需求。
特定場合加分：生日、商務活動等場合的高端陪伴服務。
如何選擇優質的高雄外送茶服務？
辨別專業合法服務的重要性
查看評價：選擇具有良好口碑的服務商。
確認價格透明：事先了解費用，避免臨時加價問題。
重視隱私保障：選擇承諾保密的合法經營商家。
服務流程簡介
聯繫商家，表達需求並獲得建議。
確定伴侶類型與服務細節。
安排時間地點，享受服務。
提升高雄外送茶體驗的建議
事先規劃：提前安排服務，避免臨時出現不便。
選擇信譽品牌：確保選擇口碑良好的服務商，避免風險。
溝通需求：明確表達需求與期待，達成雙方共識。
купить диплом ссср в нижнем тагиле [url=https://4russkiy365-diplomy.ru/]4russkiy365-diplomy.ru[/url] .
Как получить диплом техникума с упрощенным обучением в Москве официально
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
краснодар вывод из запоя [url=https://vyvod-iz-zapoya-krasnodar114.ru]краснодар вывод из запоя[/url] .
Le code promo 1xBet 2025: 1XNEW25, saississez-le lors de votre inscription pour recevoir un bonus jusqu’a $130 sur le sport. Vous pourrez aussi obtenir jusqu’a $1,500 et 150 tours gratuits sur le casino. 1xBet propose jusqu’a $130 de freebets selon le montant de votre premier depot sur les paris sportifs. Parmi eux, le bonus de bienvenue, reserve aux nouveaux inscrits sur la plateforme. Cette plateforme est classee parmi les leaders en Afrique et a travers le monde. Elle vous offre les meilleures options pour vos paris, y compris la diffusion en direct des matchs sans frais supplementaires.
Utilisez le code promo 1xBet: “1XNEW25” en 2025. Vous pourrez debloquer un bonus de bienvenue jusqu’a $130 sur les paris sportifs. Et n’oubliez pas que 1xBet offre une belle opportunite a tous les nouveaux clients. En utilisant ce code lors de votre inscription, pourrez recuperer jusqu’a $130 sur le sport et jusqu’a $1,500 en freebets et 150 tours gratuits sur le casino en ligne. Pour profiter de ce bonus exceptionnel, il vous suffit d’effectuer votre premier depot. Celui-ci vous donne droit a un bonus de 100% du montant depose, jusqu’a un maximum de $130, ou l’equivalent dans votre devise.
code promo 1xbet maroc
Как безопасно купить диплом колледжа или ПТУ в России, что важно знать
台中外送茶
台中外送茶：安全快速的外約服務指南
引言
台中外送茶是一項方便且受歡迎的服務，無論是夜晚的放鬆需求還是特殊場合的社交活動，都能提供快速、安全且專業的體驗。本文將深入探討台中外送茶的選擇、流程以及相關注意事項，幫助您在選擇服務時更加安心與滿意。
什麼是台中外送茶？
台中外送茶服務主要提供以下特點：
快速應對：透過線上或電話聯繫，立即安排外送服務。
多元選擇：服務涵蓋不同需求，從高端到實惠方案應有盡有。
隱私保障：強調保密性，確保客戶資料不被外洩。
台中外送茶適合哪些人？
商務旅客：在台中短期停留，追求品質與方便的伴侶服務。
壓力族群：希望藉由互動放鬆身心，增添生活樂趣。
聚會需求：特殊場合、生日或朋友聚會需要專業的伴侶服務。
選擇台中外送茶的注意事項
如何選擇安全的服務？
查詢評價：選擇高評價且有口碑的服務提供者。
確認價格透明：避免隱藏費用，提前溝通價格範圍。
合法經營：確認服務平台是否具備合法經營的資格。
常見的服務流程
聯繫服務商家，了解可提供的選項及價格。
確定時間與地點，確保雙方需求達成一致。
接收外送服務，享受專業的伴侶陪伴。
вывод из запоя анонимно краснодар [url=https://vyvod-iz-zapoya-krasnodar115.ru/]вывод из запоя анонимно краснодар [/url] .
купить диплом в вологде
вывод из запоя краснодар стационар [url=www.vyvod-iz-zapoya-krasnodar206.ru/]вывод из запоя краснодар стационар[/url] .
вывод из запоя краснодар [url=vyvod-iz-zapoya-krasnodar116.ru]вывод из запоя краснодар[/url] .
Services for Checking USDT for Restrictive Measures and Transfer Cleanliness: Anti-Laundering Strategies
In the up-to-date environment of virtual currencies, where fast trades and privacy are becoming the standard practice, observing the lawfulness and purity of processes is crucial. In consideration of amplified regulatory scrutiny over dirty money and terrorism financing activities, the need for effective resources to verify operations has become a key concern for cryptocurrency users. In this text, we will discuss existing services for assessing USDT for prohibitions and operation purity.
What is AML?
Anti-Laundering actions refer to a collection of supervisory protocols aimed at hindering and uncovering financial misconduct activities. With the rise of crypto usage, AML measures have become particularly crucial, allowing users to operate digital holdings securely while mitigating risks associated with sanctions.
USDT, as the preeminent recognized stablecoin, is widely used in different deals internationally. Yet, using USDT can carry several dangers, especially if your resources may relate to unclear or criminal maneuvers. To reduce these risks, it’s imperative to take make use of solutions that inspect USDT for prohibitions.
Available Services
1. Address Confirmation: Leveraging customized tools, you can verify a certain USDT address for any ties to sanction registries. This aids pinpoint potential associations to criminal conduct.
2. Operation Conduct Assessment: Some services extend analysis of transaction background, essential for measuring the transparency of financial transactions and spotting potentially hazardous conduct.
3. Surveillance Solutions: Expert monitoring systems allow you to follow all deals related to your wallet, enabling you to swiftly detect questionable operations.
4. Hazard Records: Certain platforms make available detailed threat documents, which can be valuable for traders looking to validate the trustworthiness of their holdings.
Regardless of if you are overseeing a considerable investment or performing small transactions, adhering to AML practices supports prevent legal repercussions. Utilizing USDT validation tools not only shields you from economic setbacks but also helps to establishing a safe environment for all market actors.
Conclusion
Verifying USDT for sanctions and deal purity is becoming a compulsory process for anyone eager to stay within the law and support high standards of clarity in the virtual currency domain. By interacting with trustworthy platforms, you not only secure your investments but also support to the shared goal in combating illicit finance and terrorism funding.
If you are ready to start leveraging these tools, examine the existing platforms and choose the option that most fits your demands. Be aware, knowledge is your power, and prompt operation assessment can rescue you from a variety of challenges in the time ahead.
Полезные советы по покупке диплома о высшем образовании без риска
вывод из запоя цены на дому краснодар [url=https://vyvod-iz-zapoya-krasnodar117.ru]вывод из запоя цены на дому краснодар[/url] .
Services for Assessing USDT for Restrictive Measures and Transfer Integrity: Anti-Money Laundering Solutions
In the contemporary environment of virtual currencies, where rapid trades and secrecy are becoming the norm, monitoring the legality and clarity of activities is crucial. In recognition of amplified official oversight over illicit finance and terrorism funding, the necessity for effective resources to authenticate operations has become a key matter for virtual currency users. In this piece, we will analyze existing services for checking USDT for embargoes and transfer cleanliness.
What is AML?
Anti-Laundering strategies refer to a set of supervisory protocols aimed at hindering and discovering dirty money activities. With the rise of crypto usage, AML standards have become exceedingly important, allowing individuals to manage digital resources with assurance while lessening hazards associated with embargoes.
USDT, as the arguably the popular stablecoin, is commonly used in different operations internationally. Nevertheless, using USDT can present several threats, especially if your resources may associate to opaque or illicit maneuvers. To minimize these concerns, it’s essential to take advantage of tools that inspect USDT for sanctions.
Available Services
1. Address Validation: Leveraging dedicated tools, you can confirm a particular USDT address for any links to sanction catalogs. This facilitates uncover potential ties to unlawful conduct.
2. Deal Activity Examination: Some tools offer scrutiny of transfer background, essential for assessing the transparency of financial transfers and spotting potentially hazardous activities.
3. Monitoring Services: Expert monitoring systems allow you to follow all deals related to your account, enabling you to rapidly uncover dubious actions.
4. Hazard Records: Certain services extend detailed concern reports, which can be crucial for investors looking to confirm the trustworthiness of their assets.
No matter of if you are handling a substantial capital or executing small trades, complying to AML standards supports steer clear of legal repercussions. Using USDT validation offerings not only defends you from economic declines but also supports to establishing a safe environment for all economic stakeholders.
Conclusion
Monitoring USDT for embargoes and transfer cleanliness is becoming a mandatory action for anyone enthusiastic to stay compliant within the regulations and preserve high levels of clarity in the digital asset industry. By engaging with credible solutions, you not only safeguard your resources but also contribute to the collective mission in countering dirty money and terror financing activities.
If you are prepared to start employing these tools, investigate the offered services and pick the solution that most adequately suits your requirements. Keep in mind, data is your asset, and timely deal validation can shield you from countless problems in the time ahead.
Диплом техникума купить официально с упрощенным обучением в Москве
вывод из запоя ростов-на-дону [url=https://vyvod-iz-zapoya-rostov231.ru]вывод из запоя ростов-на-дону[/url] .
вывод из запоя цены на дому ростов [url=https://vyvod-iz-zapoya-rostov233.ru]вывод из запоя цены на дому ростов[/url] .
Как получить диплом стоматолога быстро и официально
диплом о среднем образовании купить цена
можно ли купить высшее образование [url=https://4russkiy365-diplomy.ru/]можно ли купить высшее образование[/url] .
вывод из запоя цены ростов-на-дону [url=www.vyvod-iz-zapoya-rostov232.ru/]вывод из запоя цены ростов-на-дону[/url] .
вывод из запоя дешево ростов-на-дону [url=www.vyvod-iz-zapoya-rostov234.ru/]вывод из запоя дешево ростов-на-дону[/url] .
Официальная покупка диплома вуза с сокращенной программой обучения в Москве
Купить диплом специалиста в Воронеже
вывод из запоя на дому ростов-на-дону [url=http://vyvod-iz-zapoya-rostov235.ru]вывод из запоя на дому ростов-на-дону[/url] .
sport-weekend.com [url=http://vkirove.ru/news/2024/05/23/kak_vybrat_prokhodnuyu_s_turniketom_vidy_osobennosti_vybora.html]http://vkirove.ru/news/2024/05/23/kak_vybrat_prokhodnuyu_s_turniketom_vidy_osobennosti_vybora.html[/url] .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали ремонт ноутбуков fujitsu siemens рядом, можете посмотреть на сайте: ремонт ноутбуков fujitsu siemens сервис
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
clockchok.ru [url=https://www.www.deafnet.ru/info.php?c=375&id=7951]https://www.www.deafnet.ru/info.php?c=375&id=7951[/url] .
Всё, что нужно знать о покупке аттестата о среднем образовании без рисков
gtbike.ru [url=www.semstomm.ru/novosti/stacionarnyj-rentgenotelevizionnyj-introskop-osobennosti-i-primenenie/]www.semstomm.ru/novosti/stacionarnyj-rentgenotelevizionnyj-introskop-osobennosti-i-primenenie/[/url] .
wallet address verification
Solutions for Monitoring USDT for Embargoes and Operation Purity: Money Laundering Prevention Strategies
In the modern domain of digital currencies, where expedited deals and obscurity are becoming the norm, tracking the validity and clarity of transactions is crucial. In consideration of heightened administrative investigation over financial misconduct and terrorism funding, the demand for effective resources to verify transfers has become a critical issue for virtual currency users. In this piece, we will review offered offerings for monitoring USDT for embargoes and deal cleanliness.
What is AML?
AML practices refer to a set of supervisory measures aimed at preventing and uncovering dirty money activities. With the growth of virtual currency usage, AML strategies have become especially important, allowing individuals to operate digital resources confidently while mitigating risks associated with prohibitions.
USDT, as the preeminent favored stablecoin, is commonly used in different transactions internationally. Nonetheless, using USDT can present several hazards, especially if your resources may associate to ambiguous or illegal transactions. To lessen these threats, it’s imperative to take make use of offerings that inspect USDT for restrictive measures.
Available Services
1. Address Verification: Utilizing specific tools, you can inspect a designated USDT address for any links to prohibited catalogs. This helps detect potential links to illicit activities.
2. Transaction Action Examination: Some platforms make available evaluation of deal background, important for evaluating the transparency of capital movements and spotting potentially hazardous transactions.
3. Observation Systems: Expert monitoring tools allow you to observe all operations related to your location, enabling you to quickly uncover questionable activities.
4. Risk Documents: Certain tools offer detailed concern summaries, which can be helpful for stakeholders looking to confirm the integrity of their assets.
Whether of whether or not you are controlling a substantial fund or executing small transactions, complying to AML standards helps avoid legal repercussions. Using USDT certification tools not only protects you from economic setbacks but also supports to building a stable environment for all industry participants.
Conclusion
Assessing USDT for prohibitions and transfer clarity is becoming a necessary step for anyone keen to stay within the rules and preserve high benchmarks of clarity in the digital asset domain. By working with reliable solutions, you not only secure your holdings but also contribute to the common initiative in countering financial misconduct and financing of terrorism.
If you are ready to start using these solutions, review the existing services and choose the service that most adequately suits your needs. Be aware, knowledge is your advantage, and timely transfer validation can protect you from a variety of challenges in the future.
вывод. из. запоя. ростов. [url=www.vyvod-iz-zapoya-rostov236.ru]www.vyvod-iz-zapoya-rostov236.ru[/url] .
нижний новгород отели и гостиницы [url=https://otelinizhniinovgorod-ru.ru/]нижний новгород отели и гостиницы[/url] .
Anti-money laundering (AML)
Solutions for Assessing USDT for Sanctions and Transfer Purity: Anti-Laundering Approaches
In the current environment of virtual currencies, where quick trades and anonymity are becoming the norm, monitoring the legality and clarity of activities is essential. In recognition of increased government examination over illicit finance and terrorism financing activities, the requirement for efficient resources to verify transfers has become a significant priority for virtual currency users. In this piece, we will discuss existing services for monitoring USDT for prohibitions and transaction integrity.
What is AML?
Anti-Money Laundering practices refer to a series of supervisory measures aimed at stopping and detecting financial misconduct activities. With the growth of cryptocurrency usage, AML measures have become notably important, allowing participants to handle digital currencies confidently while reducing risks associated with sanctions.
USDT, as the arguably the recognized stablecoin, is broadly used in multiple transactions across the globe. Nevertheless, using USDT can carry several hazards, especially if your capital may relate to opaque or illicit transactions. To mitigate these threats, it’s vital to take leverage of solutions that check USDT for embargoes.
Available Services
1. Address Validation: Leveraging customized tools, you can check a specific USDT address for any ties to restrictive catalogs. This helps detect potential ties to illicit operations.
2. Transfer Activity Evaluation: Some offerings offer assessment of transfer history, essential for evaluating the transparency of capital transfers and spotting potentially threatening conduct.
3. Surveillance Solutions: Professional monitoring services allow you to monitor all deals related to your wallet, permitting you to swiftly detect suspicious operations.
4. Concern Statements: Certain services extend detailed concern reports, which can be crucial for investors looking to confirm the reliability of their assets.
Whether of whether you are managing a large investment or executing small deals, following to AML guidelines supports steer clear of legal repercussions. Utilizing USDT certification tools not only shields you from economic losses but also aids to forming a secure environment for all business participants.
Conclusion
Monitoring USDT for prohibitions and transfer purity is becoming a necessary process for anyone eager to continue within the rules and preserve high levels of visibility in the virtual currency domain. By interacting with trustworthy solutions, you not only protect your holdings but also help to the collective initiative in combating financial misconduct and terror financing activities.
If you are set to start leveraging these offerings, explore the accessible options and select the service that most suitably fits your preferences. Bear in mind, data is your power, and prompt deal verification can protect you from countless issues in the long run.
Как получить диплом стоматолога быстро и официально
купить диплом о высшем образовании ссср
вывод из запоя анонимно ростов [url=www.vyvod-iz-zapoya-rostov237.ru]вывод из запоя анонимно ростов[/url] .
купить диплом в асбесте [url=https://4russkiy365-diplomy.ru/]4russkiy365-diplomy.ru[/url] .
вывод из запоя на дому ростов на дону [url=https://vyvod-iz-zapoya-rostov238.ru]вывод из запоя на дому ростов на дону[/url] .
купить диплом ссср в кемерово [url=https://2orik-diploms.ru/]2orik-diploms.ru[/url] .
скорая наркологическая помощь [url=www.astana.forum24.ru/?1-1-0-00000094-000-0-0-1730874405/]скорая наркологическая помощь[/url] .
Предлагаем услуги профессиональных инженеров офицальной мастерской.
Еслли вы искали срочный ремонт ноутбуков asus, можете посмотреть на сайте: ремонт ноутбуков asus
Наши мастера оперативно устранят неисправности вашего устройства в сервисе или с выездом на дом!
스포츠 베팅 [url=www.live24bet.ru/]스포츠 베팅[/url] .
Kantorbola link alternatif login terbaru 2025 . Kunjungi link resmi situs kantor bola untuk melakukan permainan dan pendaftaran
https://bbs.fileclip.cloud/bbs/board.php?bo_table=free&wr_id=13833
неотложная наркологическая помощь в москве [url=http://superjackson.ukrbb.net/viewtopic.php?f=6&t=9765/]неотложная наркологическая помощь в москве[/url] .
вызвать наркологическую помощь [url=http://ya.7bb.ru/viewtopic.php?id=14638]http://ya.7bb.ru/viewtopic.php?id=14638[/url] .
Покупка диплома о среднем полном образовании: как избежать мошенничества?
Как правильно купить диплом колледжа и пту в России, подводные камни
купить диплом техникума в новосибирске [url=https://prema-diploms.ru/]prema-diploms.ru[/url] .
скорая наркологическая помощь в москве [url=https://www.setter.borda.ru/?1-7-0-00000685-000-0-0-1730875003]скорая наркологическая помощь в москве[/url] .