A graph is a graphical depiction of a collection of items, with certain pairs of objects connected by links. The points that connect the interconnected items are called vertices, and the ties that connect the vertices are called edges.
Data structures can be used to depict mathematical graphs. A graph can be represented as an array of vertices and a two-dimensional array of edges.
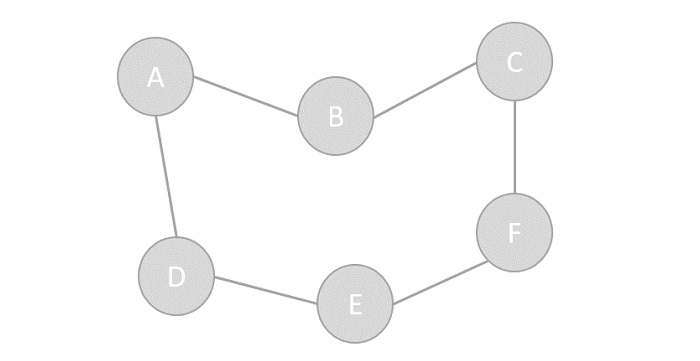
- Vertex − A vertex represents each node in the graph. The labelled circle in the following example represents vertices. As a result, A to G are vertices. We can represent them with an array, as seen in the image below. Index 0 identifies A in this case. Index 1 can be used to identify B, and so forth.
- Edge − A path or a line connecting two vertices is represented by an edge. The lines from A to B, B to C, and so on indicate edges in the following example. As demonstrated in the graphic below, we can represent an array using a two-dimensional array. AB can be represented as 1 in row 0, column 1, BC as 1 in row 1, column 2, and so on, with all other combinations remaining as 0.
- Adjacency − If two nodes or vertices are joined by an edge, they are considered neighbouring. In the example below, B is adjacent to A, C is adjacent to B, and so on.
- Path − Path represents a sequence of edges between the two vertices. In the following example, ABCD represents a path from A to D.
Basic Operations
Following are basic primary operations of a Graph −
- Add Vertex − Adds a vertex to the graph.
- Add Edge − Adds an edge between the two vertices of the graph.
- Display Vertex − Displays a vertex of the graph.
0
Pingback: 1belligerent