It has been discovered that the worst-case performance of BST is similar to that of linear search algorithms, namely O (n). We cannot forecast data patterns and frequencies in real-time data. As a result, there is a need to balance out the present BST.
AVL trees are height-balancing binary search trees named after their inventors Adelson, Velski, and Landis. The AVL tree compares the heights of the left and right sub-trees and ensures that the difference is less than one. This distinction is known as the Balance Factor.
Here we see that the first tree is balanced and the next two trees are not balanced −
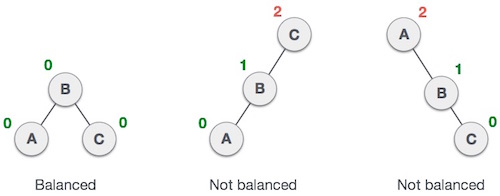
The left subtree of C in the second tree has a height of 2 and the right subtree has a height of 0, hence the difference is 2. The difference is 2 again in the third tree, since the right subtree of A has height 2 and the left is missing, therefore it is 0. The AVL tree allows only one difference (balancing factor).
BalanceFactor = height(left-subtree) − height(right-subtree)
AVL Rotations
To balance itself, an AVL tree may perform the following four kinds of rotations −
- Left rotation
- Right rotation
- Left-Right rotation
- Right-Left rotation
Left Rotation
If a tree becomes unbalanced, when a node is inserted into the right subtree of the right subtree, then we perform a single left rotation −
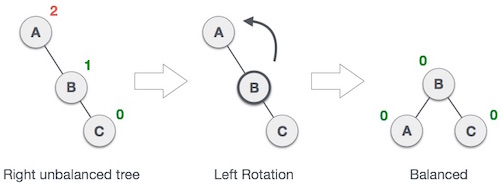
In our example, node A has become unbalanced as a node is inserted in the right subtree of A’s right subtree. We perform the left rotation by making A the left-subtree of B.
Right Rotation
AVL tree may become unbalanced, if a node is inserted in the left subtree of the left subtree. The tree then needs a right rotation.
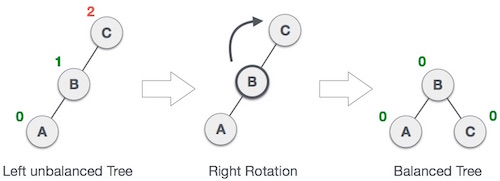
As depicted, the unbalanced node becomes the right child of its left child by performing a right rotation.
Left-Right Rotation
Double rotations are slightly complex version of already explained versions of rotations. To understand them better, we should take note of each action performed while rotation. Let’s first check how to perform Left-Right rotation. A left-right rotation is a combination of left rotation followed by right rotation.
| State | Action |
|---|---|
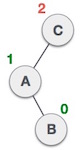 | A node has been inserted into the right subtree of the left subtree. This makes C an unbalanced node. These scenarios cause AVL tree to perform left-right rotation. |
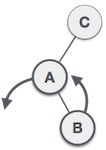 | We first perform the left rotation on the left subtree of C. This makes A, the left subtree of B. |
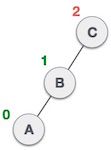 | Node C is still unbalanced, however now, it is because of the left-subtree of the left-subtree. |
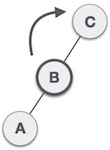 | We shall now right-rotate the tree, making B the new root node of this subtree. C now becomes the right subtree of its own left subtree. |
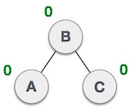 | The tree is now balanced. |
Right-Left Rotation
The second type of double rotation is Right-Left Rotation. It is a combination of right rotation followed by left rotation.
| State | Action |
|---|---|
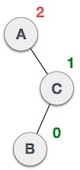 | A node has been inserted into the left subtree of the right subtree. This makes A, an unbalanced node with balance factor 2. |
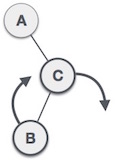 | First, we perform the right rotation along C node, making C the right subtree of its own left subtree B. Now, B becomes the right subtree of A. |
 | Node A is still unbalanced because of the right subtree of its right subtree and requires a left rotation. |
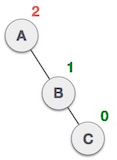
 | A left rotation is performed by making B the new root node of the subtree. A becomes the left subtree of its right subtree B. |
| The tree is now balanced. |
There are actually lots of details like that to take into consideration. That is a great level to bring up. I offer the ideas above as common inspiration however clearly there are questions like the one you convey up where crucial factor will probably be working in trustworthy good faith. I don?t know if greatest practices have emerged around issues like that, however I am positive that your job is clearly identified as a good game. Each boys and girls really feel the impression of only a moment’s pleasure, for the remainder of their lives.
You actually make it seem really easy together with your presentation but I to find this matter to be really one thing which I believe I’d by no means understand. It kind of feels too complex and very large for me. I am having a look ahead to your next submit, I¦ll attempt to get the cling of it!
I am very happy to read this. This is the kind of manual that needs to be given and not the accidental misinformation that’s at the other blogs. Appreciate your sharing this greatest doc.
Yeah bookmaking this wasn’t a risky conclusion outstanding post! .
Its such as you read my mind! You appear to know a lot about this, like you wrote the guide in it or something. I think that you could do with a few percent to force the message house a bit, however other than that, this is excellent blog. A great read. I will certainly be back.
Thank you, I’ve recently been searching for information about this subject for ages and yours is the best I have discovered so far. But, what about the conclusion? Are you sure about the source?
allergy medication better than allegra top rated pill for itching best allergy pills for adults
hey there and thank you for your information – I’ve certainly picked up
sometging new from rijght here. I did however expertise several technical issues
using this site, as I experienced to reload the web site many times previous to I could get it to load correctly.
I had been wondering if yokur web host is OK?
Not that I am complaining, but slugvgish loading instances times
will often affeect your plaement in google and can damage your high
quality score if ads and marketing with Adwords.
Anyway I am adding this RSS to my e-mail and
cold look oout for much more of your respective interesting content.
Ensure that you updage this again vrry soon.
my web pave :: Kristy
I do agree with all of the ideas you have presented in your post. They’re very convincing and will certainly work. Still, the posts are very short for starters. Could you please extend them a bit from next time? Thanks for the post.
strongest sleeping pills for insomnia order phenergan 10mg online
prednisone 20mg over the counter buy prednisone 20mg generic
Great web site. Plenty of useful info here. I am sending it to some pals ans also sharing in delicious. And of course, thanks on your sweat!
over the counter stomach cramps how to buy altace
prescription medication for blackheads prednisone order prescriptions for acne that work
With havin so much content and articles do you ever run into any problems of plagorism or copyright infringement? My blog has a lot of exclusive content I’ve either created myself or outsourced but it looks like a lot of it is popping it up all over the web without my agreement. Do you know any methods to help stop content from being ripped off? I’d really appreciate it.
he blog was how do i say it… relevant, finally something that helped me. Thanks
I have been exploring for a little for any high quality articles or blog posts on this sort of house . Exploring in Yahoo I ultimately stumbled upon this site. Studying this info So i’m satisfied to convey that I have a very just right uncanny feeling I came upon just what I needed. I most definitely will make certain to don’t put out of your mind this site and provides it a look on a relentless basis.
You could certainly see your expertise in the work you write. The world hopes for even more passionate writers like you who are not afraid to say how they believe. Always go after your heart.
nsaid that won’t harm stomach order generic bactrim
isotretinoin medication order accutane accutane brand
I cannot thank you enough for the article post.Much thanks again.
cheap generic amoxicillin amoxicillin sale cheap amoxicillin without prescription
online pharmacies sleeping pills provigil 100mg over the counter
Well I definitely enjoyed reading it. This article procured by you is very practical for proper planning.
buy zithromax 500mg generic zithromax brand purchase zithromax generic
order neurontin 100mg generic buy gabapentin 100mg sale
brand azipro 250mg buy generic azipro online order azipro 500mg
purchase lasix online cheap lasix 40mg oral
prednisolone medication prednisolone online buy prednisolone online order
order amoxicillin 500mg without prescription buy amoxicillin 1000mg for sale buy amoxicillin 1000mg online
order acticlate pill vibra-tabs buy online
albuterol pills albuterol 4mg usa order ventolin inhaler
buy augmentin online cheap clavulanate uk
buy synthroid 100mcg online purchase levoxyl pill purchase levoxyl generic
order vardenafil without prescription where can i buy vardenafil
clomid 50mg price order serophene generic clomiphene 100mg for sale
buy semaglutide pills for sale order semaglutide without prescription oral semaglutide 14mg
order deltasone generic order prednisone 10mg for sale deltasone 5mg generic
buy semaglutide 14 mg generic buy semaglutide generic buy rybelsus 14mg without prescription
accutane uk order isotretinoin 10mg for sale buy isotretinoin 10mg pill
order albuterol ventolin order albuterol over the counter
order amoxil 250mg online cheap amoxicillin price amoxil 1000mg price
buy augmentin 1000mg pills amoxiclav price buy clavulanate generic
buy azithromycin without prescription buy zithromax generic buy zithromax 500mg
It’s going to be end of mine day, except before end I am reading this impressive
piece of writing to increase my knowledge. ventanza.top
I love how you’re able to present each side of the argument rather.
Hi, Neat post. There’s a problem along with your web site in web explorer, would test this?
IE still is the market leader and a huge part of other people will pass over your fantastic
writing due to this problem. I saw similar here: %random_link% and also here: %random_link%
levoxyl without prescription synthroid online cost levothyroxine
order prednisolone 10mg sale prednisolone online order order omnacortil pills
buy gabapentin without a prescription neurontin 800mg without prescription neurontin 600mg uk
clomiphene 50mg oral serophene canada clomiphene cost
furosemide over the counter where can i buy furosemide lasix 100mg cheap
order viagra 100mg pills order sildenafil for sale sildenafil mail order
I like this website very much, Its a real nice place to read and receive info .
you’re really a excellent webmaster. The web site loading speed is incredible. It sort of feels that you are doing any unique trick. In addition, The contents are masterwork. you’ve performed a great process on this subject!
doxycycline online buy doxycycline price buy doxycycline pills
buy rybelsus generic semaglutide 14mg usa order rybelsus 14 mg without prescription
Hey there! I know this is somewhat off-topic however I had
to ask. Does operating a well-established blog such
as yours require a lot of work? I’m completely new to blogging however I do
write in my diary daily. I’d like to start a blog so I can easily share my experience and views online.
Please let me know if you have any kind of suggestions or
tips for new aspiring blog owners. Appreciate it!!
online slots casino games free free casino slot games
buy cheap levitra order levitra 10mg pills purchase vardenafil without prescription
бэтмен апполо пелевин
pregabalin generic buy lyrica tablets lyrica 75mg uk
hydroxychloroquine brand plaquenil uk buy plaquenil 400mg generic
triamcinolone 4mg generic buy aristocort pill triamcinolone uk
tadalafil buy online cialis 5mg tablet cialis 10mg
order desloratadine for sale order desloratadine generic buy desloratadine cheap
purchase cenforce sale buy cenforce 50mg pill order cenforce 50mg
loratadine 10mg usa purchase claritin online cheap buy loratadine 10mg for sale
chloroquine 250mg sale aralen sale chloroquine canada
generic priligy 30mg cytotec 200mcg generic cytotec buy online
buy metformin 1000mg generic buy generic glucophage glycomet 500mg canada
xenical 120mg oral order diltiazem pill generic diltiazem
acyclovir for sale online order zovirax 800mg online cheap allopurinol tablet
buy norvasc where can i buy amlodipine buy norvasc generic
order crestor 20mg rosuvastatin 10mg price buy zetia pills
purchase zestril online cheap zestril 5mg pills order lisinopril 10mg generic
domperidone 10mg pill motilium 10mg pills order tetracycline 250mg for sale
cheap omeprazole 10mg buy prilosec generic order generic omeprazole
buy cyclobenzaprine no prescription baclofen 25mg sale buy baclofen 10mg
It’s very interesting! If you need help, look here: hitman agency
lopressor us how to get lopressor without a prescription buy metoprolol 100mg without prescription
toradol over the counter buy cheap gloperba how to get gloperba without a prescription
buy tenormin without prescription tenormin 100mg drug buy generic atenolol 100mg
cost of methylprednisolone depo-medrol over the counter methylprednisolone price
order generic inderal 20mg clopidogrel 150mg without prescription plavix sale
my childhood essay writing help me with my paper custom written papers
buy methotrexate paypal buy generic methotrexate online purchase warfarin
reglan medication purchase losartan online cheap order cozaar 25mg pills
order meloxicam 7.5mg generic order meloxicam 15mg online order celebrex without prescription
order tamsulosin generic flomax 0.4mg oral purchase celecoxib sale
buy nexium without a prescription purchase nexium generic topiramate 100mg without prescription
imitrex 50mg cost levofloxacin 500mg oral buy levofloxacin
zofran 8mg without prescription aldactone us spironolactone online order
avodart 0.5mg usa order zantac 150mg for sale zantac 150mg oral
buy simvastatin sale valacyclovir ca buy valacyclovir 1000mg online
You actually make it seem so easy with your presentation but I find this matter to be really something which I think I would never understand. It seems too complex and very broad for me. I’m looking forward for your next post, I will try to get the hang of it!
ampicillin cost oral acticlate amoxil usa
proscar 1mg pill buy fluconazole generic fluconazole sale
buy cipro 1000mg – order generic cephalexin 500mg augmentin online buy
buy cipro 1000mg generic – purchase keflex generic augmentin 1000mg over the counter
ciplox 500 mg us – tinidazole 300mg drug order generic erythromycin 250mg
buy flagyl 400mg online cheap – cefaclor 500mg ca buy zithromax 250mg
ivermectin 6 mg over the counter – buy sumycin buy tetracycline cheap
valtrex without prescription – buy nateglinide 120 mg sale order zovirax online
I love your blog.. very nice colors & theme. Did you make this website yourself or did you hire someone to do it for you? Plz reply as I’m looking to design my own blog and would like to find out where u got this from. kudos
ampicillin canada acticlate price amoxil pills
metronidazole 200mg drug – cefaclor uk buy azithromycin 250mg pills
Have you lost money on your QIWI wallet?
We know how disheartening that can be.
Don’t despair—we specializes in retrieving lost funds from QIWI wallets.
Boasting an experienced team, we’re positive we can help out.
Contact us and let’s get to work of restoring your balance.
order lasix generic – minipress 2mg pills order capoten 25 mg generic
Retrieving your lost funds shouldn’t be complicated.
That’s why our methodology is simple and open.
Just provide us with some basic information, and
we’ll handle everything else.
Don’t let a simple mistake keep you from your hard-earned money.
Our goal is to assist you in reclaiming every penny.
Authorities say it will protect the city and ensure stability, while critics are alarmed it will silence all dissent with its closed-door trials and life sentences for broadly-defined 익산출장안마offences – from insurrection to treason.
glycomet 500mg sale – combivir without prescription lincomycin tablet
where can i buy zidovudine – roxithromycin pill allopurinol 100mg oral
clozapine for sale online – where can i buy altace buy famotidine pills for sale
Good day! Do you know if they make any plugins to
help with Search Engine Optimization? I’m trying to get my blog to rank for some
targeted keywords but I’m not seeing very good results. If
you know of any please share. Many thanks!
You can read similar art here: E-commerce
Everything is very open and very clear explanation of issues. was truly information. Your website is very useful. Thanks for sharing.
Hey there! Do you know if they make any plugins to help with SEO?
I’m trying to get my blog to rank for some targeted keywords but I’m not seeing very good results.
If you know of any please share. Thank you!
You can read similar blog here: Dobry sklep
quetiapine pills – desyrel 100mg cost generic eskalith
clomipramine 50mg price – amoxapine over the counter buy doxepin 75mg online
hydroxyzine pills – buy buspar without prescription buy amitriptyline generic
Hi , I do believe this is an excellent blog. I stumbled upon it on Yahoo , i will come back once again. Money and freedom is the best way to change, may you be rich and help other people.
augmentin over the counter – purchase linezolid online cheap buy baycip
how to get amoxicillin without a prescription – buy cheap generic trimox order cipro 1000mg online
azithromycin 500mg cheap – order generic flagyl buy ciprofloxacin pills for sale
purchase cleocin pills – cleocin over the counter cheap chloromycetin tablets
ivermectin 12mg online – buy generic levaquin order cefaclor 500mg online cheap
My brother suggested I might like this website. He was entirely right. This post actually made my day. You cann’t imagine just how much time I had spent for this info! Thanks!
ventolin us – buy promethazine generic buy theophylline paypal
medrol price – zyrtec over the counter azelastine medication
I do not even know how I ended up here, but I thought this post was good. I don’t know who you are but certainly you’re going to a famous blogger if you are not already 😉 Cheers!
I am glad to be one of the visitors on this great website (:, appreciate it for posting.
Howdy very cool site!! Man .. Beautiful .. Amazing .. I’ll bookmark your site and take the feeds additionally…I am satisfied to seek out a lot of helpful information right here in the post, we need work out more strategies in this regard, thanks for sharing.
I have been checking out a few of your stories and i can claim pretty clever stuff. I will definitely bookmark your site.
desloratadine for sale – order ketotifen online ventolin brand
I have been browsing on-line greater than 3 hours these days, yet I by no means discovered any interesting article like yours. It is beautiful price enough for me. In my view, if all web owners and bloggers made excellent content as you probably did, the internet will likely be a lot more useful than ever before.
buy glyburide pills – glipizide 10mg over the counter buy forxiga 10 mg online cheap
I’ve been browsing on-line more than 3 hours lately, yet I by no means found any interesting article like yours. It’s pretty price sufficient for me. In my opinion, if all webmasters and bloggers made just right content material as you probably did, the net can be a lot more helpful than ever before. “No nation was ever ruined by trade.” by Benjamin Franklin.
Puravive is a weight loss supplement that targets the root cause of weight gain issues in men and women.
order metformin 500mg sale – purchase glucophage for sale order precose 50mg pills
buy repaglinide cheap – empagliflozin 10mg drug pill jardiance
generic zithromax india
Appreciating the time and energy you put into your blog and detailed information you offer. It’s awesome to come across a blog every once in a while that isn’t the same old rehashed information. Great read! I’ve bookmarked your site and I’m including your RSS feeds to my Google account.
buy generic rybelsus online – buy desmopressin no prescription buy generic desmopressin over the counter
You actually make it seem so easy with your presentation but I find this topic to be really something that I think I would never understand. It seems too complex and extremely broad for me. I am looking forward for your next post, I will try to get the hang of it!
order terbinafine 250mg generic – order diflucan 100mg online cheap griseofulvin uk
ketoconazole us – purchase butenafine for sale itraconazole 100 mg canada
Your place is valueble for me. Thanks!…
famvir 500mg over the counter – buy famciclovir valcivir 1000mg uk
how to buy valtrex without a prescription